Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability
Подождите немного. Документ загружается.

258 Chapter 6
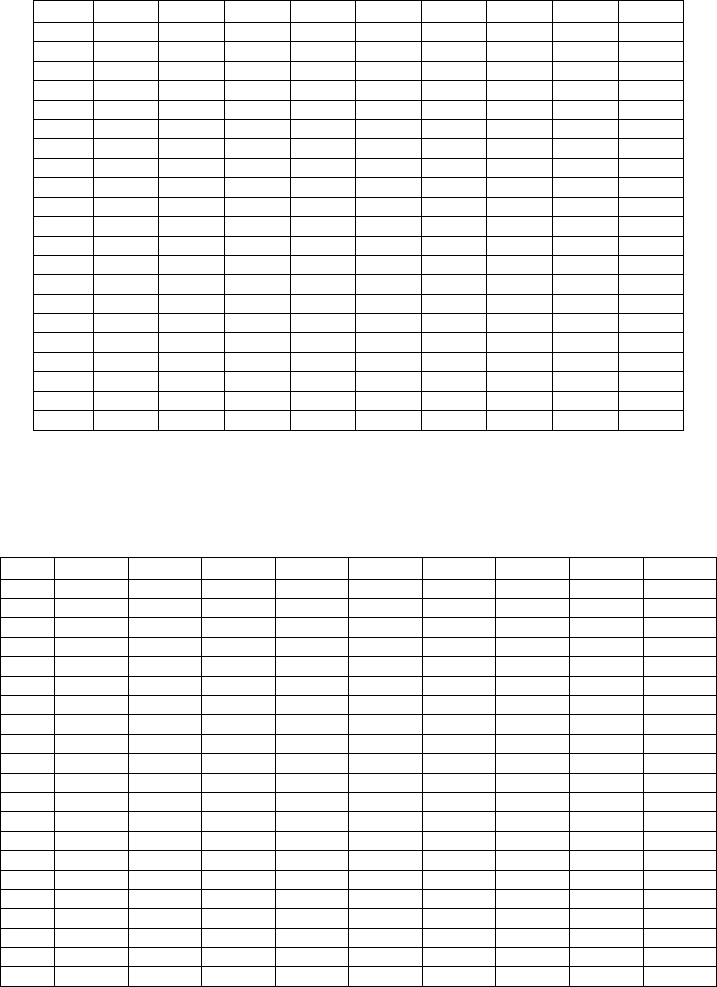
Table 3.7
gives the mean discount factors related to all the considered time
periods.
Time
1 2 3 4 5 6 7 8 9
0-1 0.9901 0.9852 0.9804 0.9756 0.9709 0.9662 0.9615 0.9569 0.9524
0-2 0.9789 0.9700 0.9603 0.9517 0.9430 0.9338 0.9249 0.9163 0.9089
0-3 0.9670 0.9532 0.9395 0.9283 0.9159 0.9029 0.8904 0.8781 0.8685
0-4 0.9543 0.9358 0.9182 0.9052 0.8897 0.8733 0.8575 0.8424 0.8312
0-5 0.9406 0.9175 0.8969 0.8827 0.8645 0.8449 0.8264 0.8089 0.7964
0-6 0.9251 0.8984 0.8755 0.8600 0.8399 0.8177 0.7967 0.7777 0.7642
0-7 0.9088 0.8785 0.8541 0.8377 0.8156 0.7919 0.7686 0.7485 0.7346
0-8 0.8911 0.8580 0.8325 0.8155 0.7919 0.7670 0.7424 0.7211 0.7072
0-9 0.8726 0.8374 0.8110 0.7935 0.7688 0.7430 0.7174 0.6956 0.6820
0-10 0.8535 0.8163 0.7897 0.7718 0.7468 0.7202 0.6938 0.6720 0.6589
3-4 0.9901 0.9852 0.9804 0.9756 0.9709 0.9662 0.9615 0.9569 0.9524
3-5 0.9785 0.9699 0.9606 0.9513 0.9429 0.9343 0.9250 0.9169 0.9097
3-6 0.9653 0.9537 0.9401 0.9271 0.9163 0.9041 0.8902 0.8803 0.8705
3-7 0.9503 0.9364 0.9190 0.9035 0.8902 0.8751 0.8578 0.8464 0.8346
3-8 0.9341 0.9177 0.8974 0.8798 0.8649 0.8472 0.8282 0.8148 0.8012
3-9 0.9163 0.8983 0.8759 0.8562 0.8401 0.8209 0.8002 0.7854 0.7705
3-10 0.8964 0.8781 0.8536 0.8328 0.8159 0.7963 0.7744 0.7580 0.7423
6-7 0.9901 0.9852 0.9804 0.9756 0.9709 0.9662 0.9615 0.9569 0.9524
6-8 0.9782 0.9687 0.9595 0.9506 0.9423 0.9341 0.9258 0.9179 0.9103
6-9 0.9641 0.9501 0.9371 0.9250 0.9148 0.9036 0.8936 0.8832 0.8728
6-10 0.9470 0.9298 0.9140 0.9005 0.8886 0.8748 0.8634 0.8522 0.8397
Table 3.7: non-homogeneous discount factors
The last results reported in
Table 3.8 give the variance matrix related to the
discount factors of
Table 3.7
time
1 2 3 4 5 6 7 8 9
0-1 0.00003 0.00002 0.00002 0.00001 0.00001 0.00001 0.00001 0.00001 0.00004
0-2 0.00007 0.00007 0.00006 0.00003 0.00002 0.00003 0.00003 0.00003 0.00011
0-3 0.00012 0.00015 0.00011 0.00006 0.00005 0.00006 0.00006 0.00007 0.00017
0-4 0.00019 0.00023 0.00016 0.00009 0.00008 0.00010 0.00009 0.00011 0.00024
0-5 0.00028 0.00032 0.00022 0.00013 0.00011 0.00015 0.00012 0.00015 0.00031
0-6 0.00037 0.00042 0.00029 0.00018 0.00015 0.00020 0.00016 0.00020 0.00038
0-7 0.00047 0.00051 0.00035 0.00024 0.00020 0.00024 0.00020 0.00025 0.00044
0-8 0.00056 0.00059 0.00042 0.00029 0.00025 0.00029 0.00024 0.00030 0.00049
0-9 0.00065 0.00067 0.00048 0.00034 0.00030 0.00034 0.00029 0.00035 0.00054
0-10 0.00073 0.00073 0.00054 0.00040 0.00035 0.00039 0.00034 0.00039 0.00058
3-4 0.00004 0.00002 0.00001 0.00002 0.00002 0.00003 0.00001 0.00003 0.00006
3-5 0.00011 0.00006 0.00005 0.00006 0.00004 0.00007 0.00003 0.00007 0.00015
3-6 0.00021 0.00012 0.00011 0.00011 0.00008 0.00012 0.00007 0.00013 0.00024
3-7 0.00032 0.00021 0.00017 0.00017 0.00013 0.00017 0.00013 0.00020 0.00032
3-8 0.00043 0.00029 0.00024 0.00023 0.00019 0.00022 0.00019 0.00026 0.00040
3-9 0.00055 0.00038 0.00031 0.00030 0.00025 0.00028 0.00026 0.00032 0.00047
3-10 0.00066 0.00047 0.00039 0.00036 0.00031 0.00035 0.00032 0.00038 0.00053
6-7 0.00005 0.00005 0.00004 0.00003 0.00002 0.00003 0.00003 0.00004 0.00008
6-8 0.00012 0.00012 0.00013 0.00008 0.00006 0.00007 0.00010 0.00012 0.00018
6-9 0.00022 0.00022 0.00022 0.00014 0.00012 0.00014 0.00018 0.00022 0.00028
6-10 0.00035 0.00032 0.00032 0.00023 0.00020 0.00022 0.00026 0.00031 0.00038
Table 3.8: variance of non-homogeneous discount factors

Finance and Insurance models 259
4 FUTURE PRICING MODEL
The discrete time Homogeneous Semi-Markov Process can also be used for
pricing futures.
Let us consider an asset observed on a discrete time scale
{
}
0,1, , , , ,tT T
<
∞…… (4.1)
having Y(t) as t market value of the future contract at time t.
In order to make the basic stochastic process
{
}
(); 0,1, ,Yt t T
=
… (4.2)
suitable to this model, it is supposed that the future has minimal and maximal
values so that the set of all possible values is the closed interval
[]
min max
,YY
partitioned in a set of m states. By letting
max min
,
1
YY
m
−
Δ=
−
(4.3)
the state space is given by:
{
}
{}
min min min min max
12
,,2,,(2),,
,,, .
m
IY Y Y Y m Y
SS S
=
+Δ + Δ + − Δ
=
…
…
(4.4)
The next step is the description of how it is possible to follow the time evolution
of a future contract by means of a DTHSMP.
Application of the homogeneous semi-Markov model requires that the state
transitions follow a homogeneous finite Markov process. Moreover it is supposed
that the waiting time in the state before a transition follows a discrete Markov
process. The last hypothesis introduces randomness in the waiting times in the
sense that, when the process arrives at a state, it can stay in this state for a
random time. The evolution equation represents the probability that the process,
once arrived at state i, representing the future value
i
S
, will be in state j at time t.
This peculiarity distinguishes the semi-Markov approach from all other
approaches in literature.
Indeed, most of the pricing models usually only introduce the Markov
assumption for state transitions.
As the states
{
}
12
,,,
m
SS S…
represent possible future values, it is not necessary
to use the interest rates, and no assumption of the term structure of interest rates
is needed as, for example in the cost of carry model (CCM), one of the most
widely used models in the literature of pricing futures contracts, using
randomness by giving a stochastic term structure of interest rates.
The model considered, as already mentioned, is homogeneous in time.
260 Chapter 6
The process evolution equation can be explained by reference to the application
shown here. Given the set of states I, that represents the set of possible prices of
the future contract, by supposing that, at time 0, the future price is
i
S , the process
evolution equation gives the probability of the future price being
j
S at time t.
Such a probability is given by the two addends:
()
ij
dt
(this is different from 0 if
and only if i=j) represents the probability that the future price is equal to the
starting price without any change in the state within a time t. The second addend
represents the probability that the future price is
j
S
at time t and that it arrives in
this state having changed states at least once.
The
()
i
t
φ
∗
represents a distribution function. Then it is also possible to compute
the expectation
[]
()
E
Yt , the variance and the value at risk (VaR).
Note that the randomness, by means of a semi-Markovian approach, is
introduced over the length of the investment. This fact, as far as the authors
know, has never been considered in derivative pricing literature.
4.1 Description Of Data
A total 7,408 records which refer to the primary future stock index market
(Fib30) bought from March 27
th
1998 to September 17
th
1998 (expiry date) have
been analysed. Each record was filled by data contained in the following fields:
Date, Operation (buy or sell), Contract amount, Price, Customer identification.
All the prices of the contracts, expressed in Italian lire, belong to the range
[27,955; 39,490]. In order to reconstruct precisely all the market movements of
future traders, the file uses only units in the field of contract amount. In such a
way, 10,394 unit financial operations made by 36 different traders are obtained.
T 0-1 1-2 2-3 3-4 4-5 5-6 6-7 7-8 8-9
# 5917 1495 707 549 445 331 209 153 86
Table 4.1.1: duration days of contract I part
T 9-10 10-11 11-12 12-13 13-14 15-16 17-17
# 6 6 6 6 10 6 6
Table 4.1.2: duration days of contract II part
The holding period of the future contract varies between a minimum of one day,
i.e., the trader holds the asset for a period variable from 0 to 24 hours (intraday),
and a maximum of 17 days. As shown in
Table 4.1, 5.917 contracts belong to the
former subclass, and only six contracts belong to the latter.
The holding periods are summarized in
Table 4.1, where the # symbol represents
the number of the futures contracts and t the holding periods, expressed in days.
Finance and Insurance models 261
In order to simplify the problem, the time is discretized into nine subclasses of
one day each, and contracts held for a time longer than eight days are also added
to the last subclass. Moreover, the future prices are discretized into 122
subclasses that are the states of the stochastic process. Each subclass is equal to
100 Italian lire and in the first class, we find the futures priced at less than 28,000
Italian lire; in the last, all the contracts having prices ranging from 40,001 to
40,100 Italian lire. We used Italian lire because we get real data for this example.
4.2 The Input Model
In order to implement the solving procedure, we need the following inputs:
m=122 (number of states of SMP).
T=9 (number of periods examined for the transient analysis of SMP).
The transition matrix
P of the embedded MC in SMP and the square lower-
triangular block matrix
T
F of order 10, the blocks of which are of order 122, are
built as follows.
First, the starting file is divided into 38 different files referring to the traders.
Then, the files are ordered on the date field and the first record with label B (buy)
is supposed to match the first record with label S (sell). In other words, the first
future sold by a certain trader, is the one bought from the same individual at the
more recent date, and so on for the subsequent records.
In this way, a new file formed by the following fields for each trader is obtained:
Buying date; Buying price; Sale date; Sale price.
Next, all the records related to a fixed holding period are taken from these files.
In this way, nine files of the holding periods
{
}
0,1, ,8… are constructed, each file
containing all the movements traders made during that fixed holding period, and
ending with the buying price and the related sale price.
Then the matrices of the holding periods are filled with the frequencies taken
from the previous files. In this way, nine square matrices of order 122, one for
each holding period, of the frequencies of the future contracts bought and sold at
the respective prices are obtained.
The elements of the matrices, the
ij
a , are the frequencies of the futures bought at
price i and sold at price j.
The transition matrix P of the embedded MC in SMP and the probability
distribution functions stored in the square lower-triangular block matrix
T
F
of
order 10, with blocks of order 122, are obtained as described in Chapter 4,
section 4.
Note that the distribution functions used as inputs for matrix
T
F are derived
directly from the raw data. Usually in other SMP applications the standard
distributions such as Poisson or Exponential were used, and only the parameters
of such distributions were estimated by means of the raw data.
262 Chapter 6
4.3 The Results
After solving the evolution equation of the semi-Markov model, a large amount
of information can be obtained. For each time
{
}
1, 2, ,tT
∈
… and for each
starting state
{
}
1, 2, ,iI m∈= … , ( )
ij
t
φ
represents the probability distributions
defined by the evolution equation DTHSMP. Unfortunately, it is not possible to
show the obtained probability distributions because of the huge amount of data
(133,956). They are, however, available upon request. After computing these
probabilities distributions it is possible to compute some statistic indices useful to
the investor.
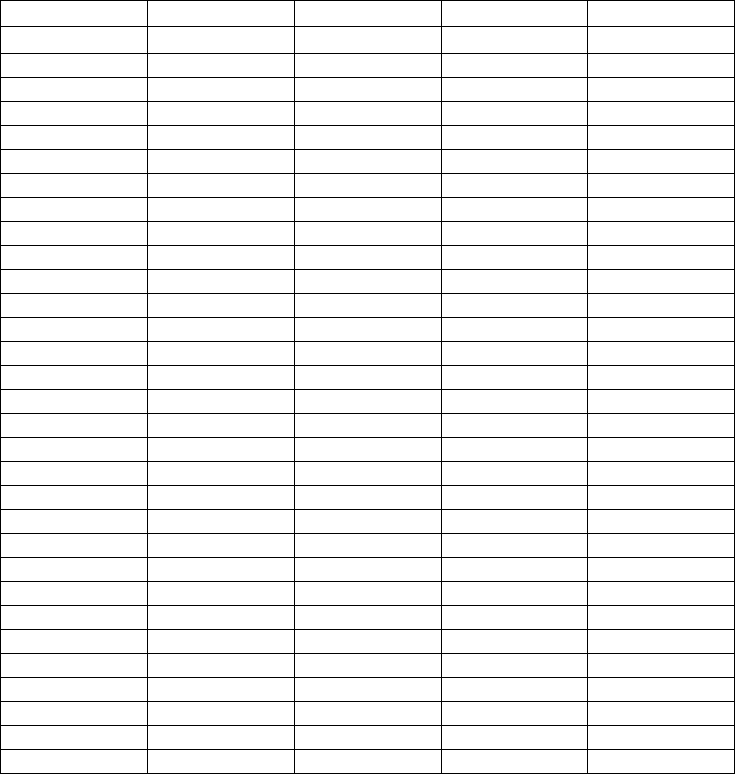
The price at time 0 (starting state), the price expectation of the future contract at
the expiry date (time 9), the corresponding sigma square, the present value at
time zero considering a risk rate per year of 4% and the corresponding value at
risk with 5% of probability are reported in
Table 4.2.
By means of the expectation value, an investor may forecast his own return with
a certain risk estimated by means of the standard deviation.
For the sake of accuracy, present values are also computed, although the time is
very short. In order to do this, the financial operations traded in a unit period time
are supposed to be made at midday. For example, the data related to the 9-th day
is discounted for 8.5 unit periods.
The value at risk (VaR), already introduced in this chapter gives the investor the
possibility of estimating a risky investment.
With the knowledge of the probability distributions ( )
ij
t
φ
, it is possible to
compute the value of the random variable with a probability less than a fixed
threshold.
When a threshold is fixed equal to 5%, the values of the last column in
Table 4.2
provide the information that, with probability 0.95, the value of the future will be
greater than the value obtained in column two of the same table, that is the VaR
value at 95%.
As our r.v. are finite, first of all, we must compute the values of k such that:
1
( ) 0.05.
k
ij
j
t
φ
=
<
∑
and
1
1
( ) 0.05.
k
ij
j
t
φ
+
=
≥
∑
Then, the values of the random variable corresponding to the kth and the k+1th
state are linearly interpolated, obtaining the hypothetical value corresponding to a
cumulated probability equal to 5%.
For brevity we report in
Table 4.2 only the first 15 and the last 15 rows of the
results.
Finance and Insurance models 263
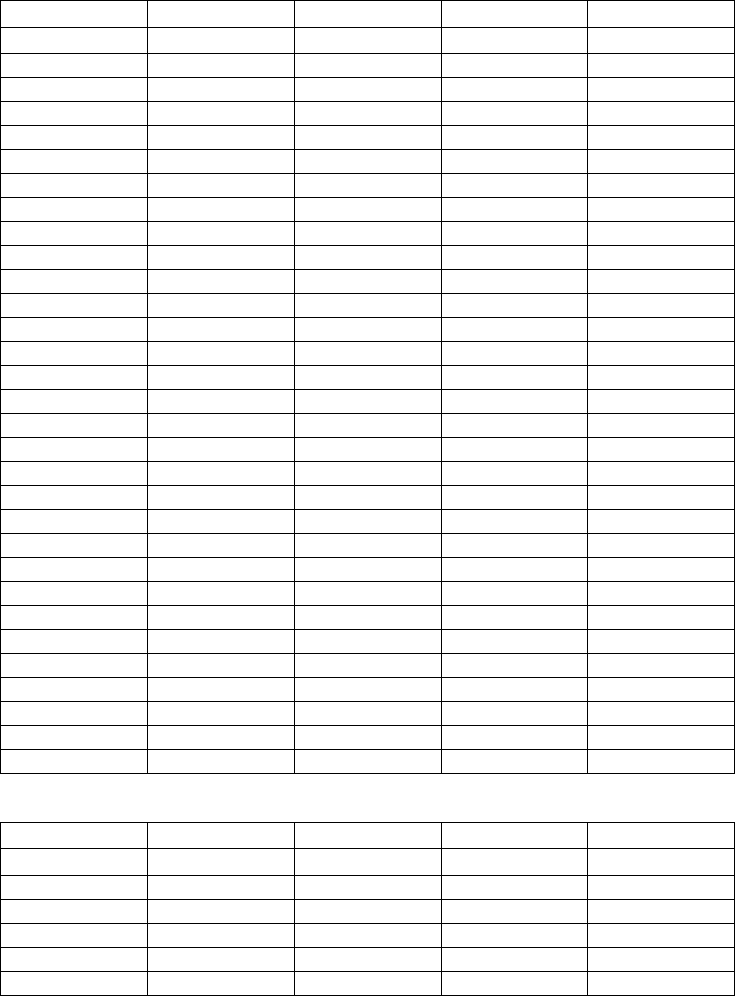
Finally, Table 4.3 and Table 4.4 present the same data that refers to time 5 and
to time 1 (intraday trading) respectively.
As we know, the latter is particularly significant to the problem we have dealt with.
Also in the last two tables, we report the first 15 and the last 15 rows of the results.
All the data including the matrix intermediate results are available upon request.
The fact that the solution of the SMP evolution equation gives probability
distributions allows the reader to easily obtain the dynamic evolution of the finan-
cial phenomenon of interest and to estimate the investment risk in different ways.
Finally, the authors would like to draw attention to the simplicity of the model
and of its use. It was, however, a rather complex procedure to turn the raw data
into input matrices, since the financial data were ready to be used for the
homogeneous Markovian models.
starting state price at time 9 sigma square p.v. at time 0 VaR
28,000 28,000 0 27,974 28,000
28,100 29,905 880 29,878 28,146
28,200 28,200 0 28,174 28,105
28,300 29,822 877 29,795 28,245
28,400 29,974 906 29,947 28,363
28,500 30,014 899 29,987 28,412
28,600 30,002 929 29,975 28,386
28,700 30,056 879 30,028 28,526
28,800 29,894 874 29,867 28,492
28,900 30,124 914 30,096 28,462
29,000 29,948 805 29,921 28,510
29,100 30,272 954 30,244 28,449
29,200 30,243 1,104 30,215 28,442
29,300 30,115 975 30,087 28,393
29,400 30,090 931 30,062 28,317
38,700 37,965 517 37,930 37,312
38,800 38,460 442 38,425 37,784
38,900 38,900 0 38,864 38,805
39,000 39,000 0 38,964 38,905
39,100 38,079 555 38,045 37,317
39,200 38,756 587 38,720 37,807
39,300 39,300 0 39,264 39,205
39,400 38,115 567 38,080 36,930
39,500 39,500 0 39,464 39,405
39,600 39,600 0 39,564 39,505
39,700 39,700 0 39,664 39,605
39,800 39,800 0 39,764 39,705
39,900 39,900 0 39,864 39,805
40,000 40,000 0 39,963 39,905
40,100 40,100 0 40,063 40,005
Table 4.2: Value at expiry date
264 Chapter 6
starting state price at time 5 sigma square p.v. at time 0 VaR
28,000 28,000 0 27,986 28,000
28,100 29,024 626 29,010 28,343
28,200 28,200 0 28,186 28,105
28,300 29,193 445 29,179 28,536
28,400 29,317 727 29,303 28,401
28,500 29,452 411 29,438 28,706
28,600 29,624 631 29,610 28,571
28,700 29,863 548 29,848 29,001
28,800 29,686 412 29,671 29,303
28,900 29,706 521 29,692 28,826
29,000 29,964 401 29,949 29,426
29,100 29,978 566 29,963 29,048
29,200 29,769 1,071 29,754 28,099
29,300 29,962 821 29,947 28,791
29,400 29,897 807 29,882 28,770
38,700 38,615 288 38,597 37,930
38,800 38,813 286 38,794 38,215
38,900 38,900 0 38,881 38,805
39,000 39,000 0 38,981 38,905
39,100 38,539 307 38,520 37,850
39,200 38,818 471 38,799 38,025
39,300 39,300 0 39,281 39,205
39,400 38,178 325 38,159 37,829
39,500 39,500 0 39,481 39,405
39,600 39,600 0 39,581 39,505
39,700 39,700 0 39,681 39,605
39,800 39,800 0 39,781 39,705
39,900 39,900 0 39,881 39,805
40,000 40,000 0 39,981 39,905
40,100 40,100 0 40,081 40,005
Table 4.3: Value after five days
starting state intraday price sigma square p.v. at time 0 VaR
28,000 28,000 0 27,998 28,000
28,100 28,484 112 28,482 28,303
28,200 28,200 0 28,198 28,105
28,300 28,732 122 28,730 28,504
28,400 28,563 222 28,562 28,315

Finance and Insurance models 265
28,500 28,644 150 28,642 28,410
28,600 28,926 340 28,925 28,514
28,700 28,892 200 28,890 28,610
28,800 28,800 0 28,798 28,705
28,900 29,017 293 29,015 28,806
29,000 29,000 0 28,998 28,905
29,100 29,356 504 29,354 29,007
29,200 29,608 527 29,606 29,110
29,300 29,684 288 29,682 29,214
29,400 29,784 450 29,782 29,310
38,700 38,719 39 38,717 38,606
38,800 38,877 158 38,875 38,706
38,900 38,900 0 38,898 38,805
39,000 39,000 0 38,998 38,905
39,100 39,100 0 39,098 39,005
39,200 39,227 45 39,225 39,107
39,300 39,300 0 39,298 39,205
39,400 39,400 0 39,398 39,305
39,500 39,500 0 39,498 39,405
39,600 39,600 0 39,598 39,505
39,700 39,700 0 39,698 39,605
39,800 39,800 0 39,798 39,705
39,900 39,900 0 39,898 39,805
40,000 40,000 0 39,998 39,905
40,100 40,100 0 40,098 40,005
Table 4.4: Intraday values
5 A SOCIAL SECURITY APPLICATION WITH REAL
DATA
5.1 The Transient Case Study
The example is similar to the one given in Chapter 2, section 9.7 and in Chapter 3
section 13 but real life data will now be used with the same invalidity degrees.
Let us recall that the aim is to calculate in particular the average degree of
disablement to be expected in given epochs, in view of determining the
premiums to be paid to the insuring agency by employers in connection with
disabling professional diseases.
We assume that the temporal evolution of the disabling disease is the same as in
the examples mentioned above.
The data selected for the numerical experiment reflects the situation with
disabling professional diseases in Campania (Italian region) from 1945 to 1978.

266 Chapter 6
They were obtained from about 800 case histories of workers suffering from
professional diseases.
The average degree of disablement is calculated according to the following
expression:
1
() ()
m
iijj
j
St tS
φ
=
=
∑
(5.1)
for a fixed time t, with
j
S representing the upper bound disability degree inside
the jth state.
Result (5.1) is similar to (13.2) of Chapter 3, but here, we will obtain results in
transient instead of immediately working asymptotically as before (see result
13.3 of Chapter 3).
Furthermore, for
P and F we used the following estimators:
ij
ij
i
n
p
n
=
(5.2)
where
ij
n is the number of transitions from
i
S to
j
S and
i
n is the number of
observed elements in
i
S
;
() 1
ij
t
ij
Ft e
λ
−
=−
(5.3)
where
ij
λ
is the estimated mean sojourn time in state
i
S given the state
j
S
successively visited.
The mean degree of disablement was calculated for epochs of 10, 20 and 30
years.
Table 5.1 shows matrix P and Table 5.2 gives the degree of disablement at 10,
20 and 30 years, computed by means of (5.1).
The ( )t
Φ matrices, here omitted for the sake of brevity, were calculated by the
program at discrete epochs 1, 2, ..., 10, ..., 20, ...,30.
Table 5.3 shows the results obtained for the mean degree of disablement at 10,
20 and 30 years, that are practically identical to those obtained by (De Dominicis
and Manca (1984b)) using the same data with an asymptotic expression for ( )
ij
t
φ
as t →∞ and leading to an asymptotic mean degree of disablement of 82.75%.
The result is also consistent with that obtained by (De Dominicis and Manca
(1984b)) using, in the asymptotic case, a stationary MC, yielding a mean degree
of 82.85%.
On the basis of Dutch data, and using a stationary MC model, (Yntema (1965))
found a value of 79 %, as shown in Chapter 2, result (9.122))
In spite of the fact that the approaches followed in the two cases (transient and
asymptotic) are quite different, it is interesting to note the fast convergence of the
present method to the asymptotic value.
Finance and Insurance models 267
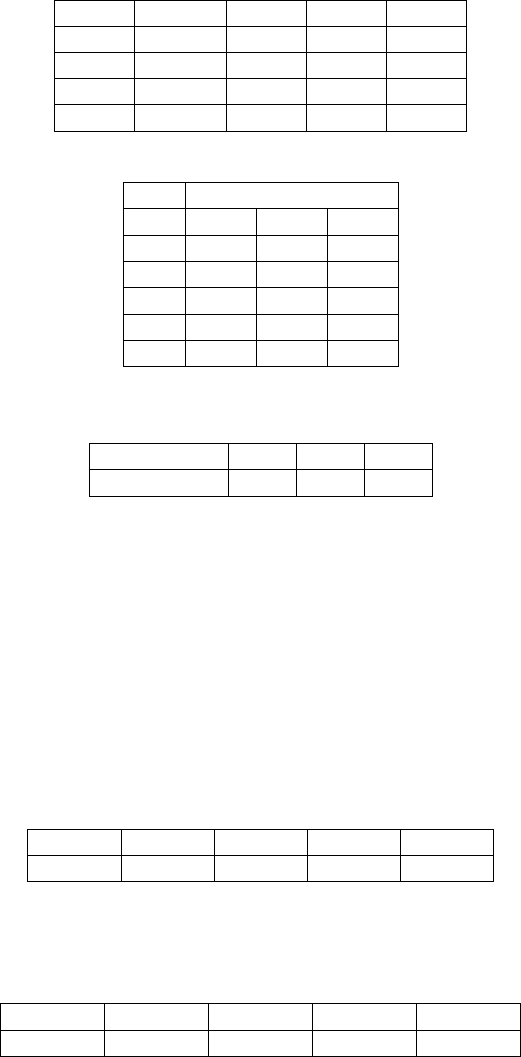
.00000 .82629 .16012 .00906 .00453
.00273 .01639 .85247 .11475 .01366
.00000 .01869 .05607 .68225 .24299
.00000 .00000 .03279 .01639 .95082
Table 5.1: transition probabilities of the embedded Markov Chain
years
state 10 20 30
1 33.70 34.38 34.43
2 34.12 34.40 34.44
3 52.94 53.22 53.25
4 74.99 75.20 75.21
5 98.09 98.06 98.06
Table 5.2. Mean degree of disablement at 10, 20 and 30 years conditioned by
the state of entry in the system.
Years 10 20 30
Mean degree 82.96 83.04 83.05
Table 5.3: Total mean disability degree at 10, 20 and 30 years
5.2 The Asymptotic Case
For the same data, we also study the asymptotic behaviour of the HSMP chain
given before.
Figure 5.1 presents the graph related to the transition matrix P given in Table 5.1.
From the graph it is easy to understand that the related Markov Chain is
irreducible because it is possible to go from one state to all the other states.
In this case the stationary probability vector of the embedded Markov chain can
be computed and is reported in
Table 5.4.
1 2 3 4 5
0.00061 0.03669 0.22228 0.11365 0.62677
Table 5.4: Markov stationary probability vector
From the irreducibility of the Markov chain, it is possible to compute the ( )
ij
φ
∞
that are given in
Table 5.5.
1 2 3 4 5
0.000366 0.036774 0.222061 0.117726 0.623073
.00000 1.00000 .00000 .00000 .00000
Table 5.5: semi-Markov stationary probability vector
