Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability

288 Chapter 7

1,0,

()

0, 0,

x

ex

Ax

x

λ

−

⎧

−

≥

=

⎨

<

⎩

(1.36)

so that, by relation (1.2):

1

α

λ

=

. (1.37)

Condition (1.13) or (1.32) becomes:

.c

λ

β

> (1.38)

So, if in general, any Andersen model is defined by two general d.f. A and B on

0,∞[), which, as we already know, justifies the notation G/G model where letter

G stands for "general", on the other hand, any Cramer-Lundberg model is defined

by a strictly positive parameter

λ

, defining the Poisson process of claim arrivals

and by a general d.f. B on

[

)

0,

∞

for claim amounts. This also explains the

notation P/G (P for "Poisson" and G for "general") for this particular model.

1.2.2 The Ruin Probability

Now we will see how it is possible to build specific mathematical treatments to

obtain simple results concerning the non-ruin probability function

φ

.

From now on, we will suppose that condition (1.38) is satisfied; otherwise,

φ

is

identically 0.

From standard rules of probability, we get, by conditioning with respect to the

first claim occurrence time,

00

() ( ) () , 0.

uct

t

ue uctydBydtu

λ

φλφ

∞+

−

=+−>

∫∫

(1.39)

By the change of variables z=u+ct, we get:

0

() ( ) () .

uz

z

cc

c

uee zydBydz

c

λλ

λ

φφ

−

∞

=−

∫∫

(1.40)

From classical theorems of analysis, it follows from this last expression that

φ

is

derivable and that its derivative can be computed as follows:

0

'( ) ' ( ) ( )

()().

uz

z

cc

u

uu

u

cc

ue e zydBydz

c

ee zydBy

c

λλ

λ

φφ

λ

φ

−

∞

⎛⎞

=−

⎜⎟

⎝⎠

⎛⎞

+− −

⎜⎟

⎝⎠

∫∫

∫

(1.41)

Using relation (1.40) again, we get:

0

'( ) ( ) ( ) ( ).

u

uu uydBy

cc

λλ

φφ φ

=− −

∫

(1.42)

We will now integrate this last equality term by term on [0,t] to obtain:

Insurance risk models 289

000

() (0) ( ) ( ) ( ) .

tt

tdydByd

cc

ξ

λλ

φ

φφξξφξ ξ

−= − −

∫∫∫

(1.43)

Using Fubini's theorem related to the permutation of integration for the last term

of the second member of (1.43), we get:

00

() (0) ( ) ( ) ( ) .

tty

t

tdydByd

cc

λλ

φ

φφξξφξ ξ

−= − −

∫∫∫

(1.44)

The double integral of the second member can be integrated by parts, with:

0

() () ( ( ) ), () ().

ty

t

y

f

yd yddgydBy

φν ν φξ ξ

−

==− =

∫∫

(1.45)

This leads to the following result:

0

() (0) ( ) ( ) ( ) .

t

tdtyBydy

cc

λλ

φφ φξξ φ

−= − −

∫

(1.46)

Finally, setting ty

ξ

=− in the first integral of this last relation, we get:

0

() (0) ( )(1 ( ) .

t

ttyBydy

c

λ

φφ φ

=+ −−

∫

(1.47)

Before solving this integral equation, we have to compute the value of (0)

φ

. To

do so, we let t tend toward

∞

in the last relation; it follows that:

() (0) ()()L

c

λ

φφ φ

∞

=+∞∞ (1.48)

where: dL(y)=[1-B(y)]dy and so

0

() (1 ()) .LBydy

β

∞

=− =

∫

(1.49)

Now, coming back to the equality (1.48), we can extract the value of ( )

φ

∞ :

(0)

() ,

1

c

φ

λ

β

∞=

−

(1.50)

but, by condition (1.38), we have ( )

φ

∞

=1 and so the last relation gives the

desired result:

(0) 1 .

c

λ

β

φ

=−

(1.51)

The final form of the integral equation (1.39) is thus:

0

() 1 ( ) *( ),

1

*( ) (1 ( )) .

t

y

ttydBy

cc

By Bzdz

λ

βλβ

φφ

β

=− + −

=−

∫

(1.52)

We can easily solve this integral equation using the Laplace transform. With the

same conventions as in Chapter 2, relation (1.52) leads to

290 Chapter 7

1

() 1 () *()

s

sb s

cs c

λβ λβ

φφ

⎛⎞

=− +

⎜⎟

⎝⎠





(1.53)

where:

1()

*( ) .

B

y

by

β

−

= (1.54)

From the algebraic equation (1.53) we can obtain an explicit expression of the

Laplace transform of the probability of non-ruin

φ

:

1

() .

1*()

cs

s

bs

c

λβ

φ

λβ

⎛⎞

−

⎜⎟

⎝⎠

=

⎛⎞

−

⎜⎟

⎝⎠



(1.55)

Using assumption (1.38), we get

1*()1*(0)1 0,0,bs b s

ccc

λ

βλβλβ

−>−>−>∀>



(1.56)

so that

*( ) 1, 0.bs s

c

λ

β

<

∀>



(1.57)

By a series expansion, the new expression of the Laplace transform of

φ

is:

0

1

() 1 *() .

n

sbs

cs c

λβ λβ

φ

∞

=

⎛⎞⎛ ⎞

=−

⎜⎟⎜ ⎟

⎝⎠⎝ ⎠

∑



(1.58)

By inverting this last relation member by member, we get an explicit form of the

non-ruin probability:

()

0

() 1 *() .

n

uBu

cc

λβ λβ

φ

∞

=

⎛⎞⎛⎞

=−

⎜⎟⎜⎟

⎝⎠⎝⎠

∑

(1.59)

If we want to express the probability of ruin at u, we have from equality (1.24):

()

0

()

0

() 1 *()) ,

1 (1 *( )) .

n

uBu

cc

Bu

cc

λβ λβ

∞

=

∞

=

⎛⎞⎛⎞

Ψ=−

⎜⎟⎜⎟

⎝⎠⎝⎠

⎛⎞⎛⎞

=− −

⎜⎟⎜⎟

⎝⎠⎝⎠

∑

(1.60)

This result was proved by Janssen (1969a).

Example 1.1 The P/P model or Lundberg's model

The notation P/P means that we must drastically particularize the choice of the

d.f. B as a negative exponential one so that:

1

1,0,

()

0, 0.

y

ey

By

y

β

−

⎧

⎪

−

≥

=

⎨

⎪

<

⎩

(1.61)

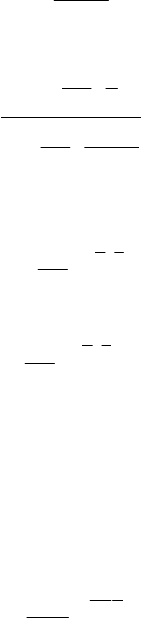
Insurance risk models 291

As here:

*( ) ( )

B

yBy

=

, (1.62)

we deduce that:

1

*( )

1

bs

s

β

=

+



(1.63)

and it suffices to use result (1.55) to get:

1

() .

1

cs

s

cs

λβ

φ

λβ

β

⎛⎞

−

⎜⎟

⎝⎠

=

⎛⎞

−

⎜⎟

+

⎝⎠



(1.64)

Taking the inverse Laplace transform for both members of this last relation, we

find that:

1

() 1

u

c

ue

c

λ

β

λβ

φ

⎛⎞

−−

⎜⎟

⎝⎠

=−

(1.65)

and of course:

1

()

u

c

ue

c

λ

β

λβ

⎛⎞

−−

⎜⎟

⎝⎠

Ψ= . (1.66)

The existence of such simple explicit formulas is exceptional in risk theory

because it gives very simple expressions for

and

φ

Ψ

.

Let us also mention that we can write another expression for

Ψ

; indeed, we

know from relation (1.12) that:

(1 ).c

λ

βη

=

+ (1.67)

Substituting c given by this expression in relation (1.66) leads to the new

expression:

1

() .

1

u

ue

η

β

η

−

+

Ψ=

+

(1.68)

This gives the surprising result that, providing relation (1.38) is satisfied, that is:

c

λ

β

>

, the ruin probability only depends on

η

and

β

but not on

λ

.

In other words, this result means that if we have two insurance companies having

for the P/P model respectively the parameters

12

(,), (,)

λ

βλβ

, both couples

satisfying inequality (1.38), then these two companies, starting with identical

equities, have the same ruin probability iff they use the same security loading

η

So, in this case, from the point of view of ruin theory, the company having the

largest parameter

λ

is not more dangerous than the other provided that both

companies have the same mean claim amount and security loading.

292 Chapter 7

Example 1.2

1) Let us consider an insurance company having as annual mean of claim

amounts 2 billions € and 50 000 as mean claim number per year and as initial

reserve u an amount of 8 000 000 €.

Using our notation, we see that for the considered company:

50000,

2000000000, 8000000u

λ

λβ

=

==

(1.69)

and so:

40000.

β

=

(1.70)

From relation (1.68), we get:

200

1

(8000000) .

1

e

η

−

+

Ψ=

+

(1.71)

Table 1.1 gives some values of this ruin probability as a function of the loading

factor.

loading ruin probability

0.01 0.1366752

0.03 0.0028661

0.05 0.0000696

0.07 0.0000019

0.10 0.000000011544

Table 1.1

2) Now let us suppose that the loading factor is fixed at 7% and let us see what

happens if:

(i) the initial reserve has successively the following values:

4 000 000, 2 000 000, 1 000 000, 500 000,

(ii) with a reserve of 8 000 000, the mean claim amount has as values 25 000 and

100 000,

(iii) the annual mean claim number has as values successively 70 000, 20 000,

still with a reserve of 8 000 000.

The results are the following:

(i)

0.07

1.07 40000

0.0654206

40000

1

(2000000) ,

1.07

0.9345794

u

e

−⋅

−

Ψ=

=

(1.72)

and so we get the results in

Table 1.2.

reserve Ruin probability

4 000 000 0.0073472

2 000 000 0.0354835

1 000 000 0.1821047

500 000 0. 4125424

Table 1.2

Insurance risk models 293

(ii) Here we get:

0.07 8 000 000

1.07

0.0654206

1

(8000000) ,

1, 07

0.9345794

u

e

β

−⋅

−

Ψ=

=

and so we get the results given in

Table 1.3:

mean claim amount ruin probability

25 000 0. 00000000075655

150 000 0. 0285312

Table 1.3

(iii) In case of an annual mean claim number having as values successively

70 000, 20 000, still with a reserve of 8 000 000, the annual mean of claim

amounts has the values 2.8 billions and 800 millions. For the annual mean

incomes, we get respectively 996 billions, 856 000 000.

Nevertheless, the ruin probability remains equal to 0.0000019.

1.2.3 Risk Management Using Ruin Probability

The explicit result (1.68) easily gives the solution of the three basic problems in

risk management for an insurance company.

Problem 1 Given the basic data ( , , )

λ

βη

of the company and the initial reserve

amount u, how are we to measure the risk exposure of the company?

It suffices to use result (1.68) to compute the ruin probability on

[

)

0,

∞

.

Problem 2 Given the data

(, )

λ

β

of the company and the initial reserve amount

u, how are we to measure the loading security so that the ruin probability on

[

)

0,∞ will never exceed a critical value (1

ε

−

)?

Using result (1.68) again, we must solve the inequality:

1

u

e

η

ηβ

ε

η

−

+

<

−

+

(1.73)

or the equality:

ln(1 ) ln(1 )

1

u

η

ε

ηβ

−++ =−

+

(1.74)

294 Chapter 7

which can be done using the Newton method.

Problem 3 Given the data

(, )

λ

β

of the company and the loading security, how

are we to measure the initial reserve amount u so that the ruin probability on

[

)

0,∞ will never exceed a critical value 1-

ε

?

Using result (1.68) again, we must solve the inequality:

1

u

e

η

ηβ

ε

η

−

+

<

−

+

(1.75)

or the equality:

ln(1 ) ln(1 )

1

u

η

ε

ηβ

−++ =−

+

(1.76)

which has as unique solution:

1

ln( (1 )).

η

β

ηη

η

+

+ (1.77)

1.2.4 Cramer’s estimator

In the preceding section, we find an explicit expression for the ruin probability

ψ using result (1.60). To get a more useful result, from the computational point

of view, the only possibility is to obtain simple and good approximations of the

function

Ψ

.

To do this, we start from the integral equation (1.52) and we express the ruin

probability Ψ using relation (1.23). We get

0

( ) (1 *( )) ( ) *( ).

t

tBt tydBy

cc

λβ λβ

Ψ= − + Ψ−

∫

(1.78)

From condition (1.38), we have:

0

*( ) 1dB y

cc

λβ λβ

∞

<

∫

(1.79)

and so it follows that the integral equation (1.78) is not of renewal type;

nevertheless, it is said to be of defective renewal type.

To be able to apply results of renewal theory from Chapter 2, we have to get

around this difficulty; that is why we will pose:

ˆ

() ()

Rt

te tΨ=Ψ (1.80)

where R is a positive constant.

Consequently, the integral equation (1.78) can now be written in the form

0

ˆˆ

() (1 *()) ( *( )).

t

Rt Rt Rt

et Bt eetydBy

cc

λ

βλβ

−−−

Ψ= − + Ψ−

∫

(1.81)

Multiplying both members of this last equality by e

Rt

, we get:

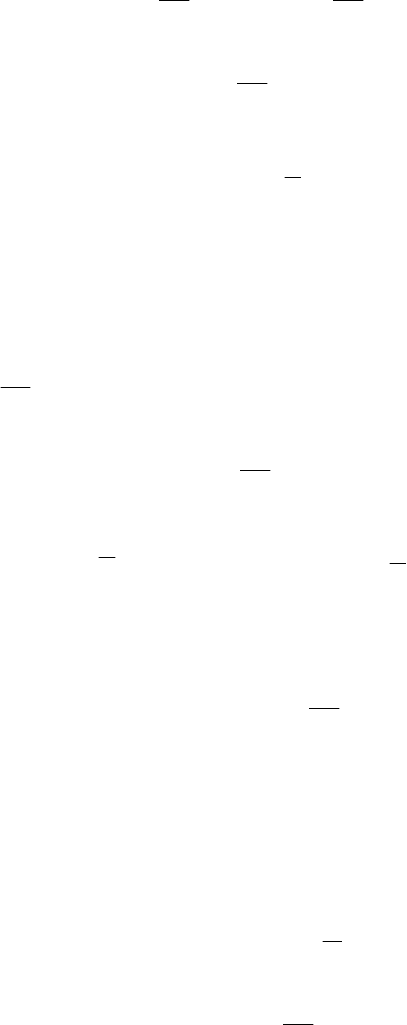
Insurance risk models 295

0

ˆˆ

() (1 *()) ( *( ))

t

Rt Rt

tBteetydBy

cc

λβ λβ

−

Ψ= − + Ψ−

∫

. (1.82)

This last equation will be of renewal type provided that

0

*( ) 1,

Ry

edB y

c

λβ

∞

=

∫

(1.83)

i.e., by relation (1.52), iff the function from

[

)

0, ,

+

∞ 

(1 ( )),

Ry

yeBy

c

λ

−

(1.84)

is a density function.

Now using the key renewal theorem (

Proposition 4.2 of Chapter 2), we are able

to prove the following fundamental result.

Proposition 1.1 (Cramer's estimator of ruin theory)

If:

(i)

1,

c

λβ

< (1.85)

(ii) there exists a positive constant R such that:

0

*( ) 1

Ry

edB y

c

λβ

∞

=

∫

(1.86)

and

0

() (1()) ,

Ry

myeBydy

c

λ

∞

=−<∞

∫

0

() (1()) 1,

Ry

myeBydy

c

λ

∞

=

−=

∫

(1.87)

then, the following approximation formula is valid:

()

u

uCe

λ

−

Ψ≈ (1.88)

where the constant C has as value:

1

1().CRcm

c

λβ

−

⎛⎞

=−

⎜⎟

⎝⎠

(1.89)

Proof It can be shown that under our assumptions, the function

[

)

0,

+

∞  :

(1 * ( ))

Ry

ye By− (1.90)

is directly Riemann integrable (see Çinlar (1975b) for the definition))

We can thus use the key renewal theorem (see

Proposition 4.2, Chapter 2) to

obtain from the integral equation of renewal type (1.82):

0

1

ˆ

lim ( ) ( )

t

tGxdx

m

∞

→∞

Ψ=

∫

(1.91)

with

() (1 *())

Rx

Gx e B x

c

λβ

=− (1.92)

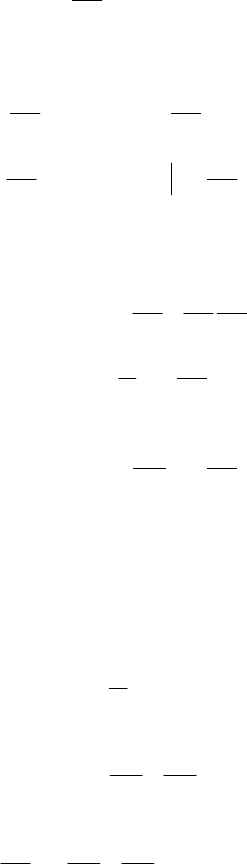
296 Chapter 7

and

0

*( ).

Ry

medBy

c

λβ

∞

=

∫

(1.93)

By integrating both members of relation (1.92), we get with an integration by

parts for the second member:

0

() (1 *())

= (1 *( )) *( ).

Rx

Rx Rx

e

Gxdx B x d

cR

B

xe edB x

cR cR

λβ

λβ λβ

∞

=−

−+

∫∫

∫

(1.94)

By the direct Riemann integrability of function (1.90), the bracket has value zero

at +

∞. Moreover, using assumption (1.86) to deal with the second term of the

second member of this last equality, we get:

0

() ,

1

1 .

c

Gxdx

cR cR

Rc

λβ λβ

λ

β

λβ

∞

=− +

⎛⎞

=−

⎜⎟

⎝⎠

∫

(1.95)

Using relations (1.80), (1.91) and (1.95) finally gives:

1

lim ( ) 1 ,

,

Ru

u

ue

mR c

C

λ

β

→∞

⎛⎞

Ψ=−

⎜⎟

⎝⎠

=

(1.96)

and so the theorem is proved. 

Before giving the next result, we must first write the basic assumption (1.86) of

Proposition 1.1 under another form. To do this transformation, let us begin to

express the integral

00

1

*( ) (1 ( )) ;

Ry Ry

edB y e Bydy

β

∞∞

=−

∫∫

(1.97)

using an integration by parts for the second member we obtain:

00

11

*( ) ( ).

Ry Ry

edB y edBy

RR

ββ

∞∞

=− +

∫∫

(1.98)

Thus, assumption (1.86) becomes:

0

11

()

Ry

c

edBy

RR

λβ β β

∞

=− +

∫

(1.99)

or equivalently:

0

().

Ry

R

cedBy

λλ

∞

+=

∫

(1.100)

This new form of the R-equation (1.100) is called the Cramer-Lundberg

equation.

Insurance risk models 297

This equation clearly shows that the existence of a finite positive value of R

implies the existence of the generating function of the d. f. B, at least on [0,R],

and consequently that this d.f. has moments of every order.

The Cramer-Lundberg equation has a simple geometric interpretation as the

value of R is given by the strictly positive value of the intersection point of the

curve representing the function

0

()

Ry

R

ye dB y

λ

∞

∫

 and the straight line d whose

equation is given by the first member of equation (1.100).

It follows that the slope of the tangent t at the curve C at the origin has the value

.

λ

β

From relation (1.85), this value is strictly less than the slope c of d.

Moreover, it is easily seen that the function defined by the second member of the

Cramer-Lundberg equation is a strictly increasing convex function. This implies

that this equation has only one strictly positive solution R.

It can be shown that the value R is strictly less than 1 (see for example Gerber

(1979)).

The next result gives an interesting upper bound of the ruin probability.

Corollary 1.1 Under the assumptions of Proposition 1.1, the following inequality

is true for all positive u:

() .

R

u

ue

−

Ψ≤ (1.101)

Proof Using the r.v. defined by:

0

(),

, 0,1,...,

0,

nn nn

n

nn

k

Z

ZcXY

SZn

S

=

=− = −

==

=

∑



(1.102)

we can write for, ( )

n

uΨ , the probability of being ruined by one of the first n

claims (n=1,2,...):

{

}

0

( ) (inf ,..., )

nn

uP S S uΨ= ≤−



. (1.103)

Of course, since

0

0S =



we can extend the definition of ( )

n

u

Ψ

for negative

values of u so that:

() 1, 0.

n

uu

Ψ

=< (1.104)

Since

() lim ()

n

uu

→∞

Ψ

=Ψ

, (1.105)

and since the ruin event can only occur upon the arrival of a claim, it suffices to

show that for all real value of u:

( ) , 0,1,...

Ru

n

ue n

−

Ψ≤ = . (1.106)

For n=0, the result is obvious since:

Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability

Подождите немного. Документ загружается.