Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability
Подождите немного. Документ загружается.


328 Chapter 7
If all the
k
λ
are equal to
λ
, we have a P/SM model for which the last relation
becomes:
() ().
s
ll
l
uu
φπφ
=
∑
(3.121)
(iii) If
1,c ≠
it suffices to replace in the above formulas,
i
λ
by / , 1,..., .
i
ci m
λ
=
3.5.4 The Zero Order Models As Special Case Of The Model M/SM
3.5.4.1 The P/SM(0) model
In section 3.5.1, for the Zero Order Model SM(0)/SM(0) we established the
equality of all the non-ruin probabilities
, 1,..., .
i
im
φ
=
As for the
P/SM(0) model, we have:
0, 0,
() ()
1,0,
AA
x
x
Fx Fx
ex
λ
−
<
⎧
==
⎨
−
≥
⎩
(3.122)
we know from relation (3.97) that:
() ( ( ) ()
rBA
jj
j
Qu F zd F
π
ξξ
+∞
−∞
=+
∑
∫
(3.123)
and consequently, the
G/G associated model becomes here a P/G model with
() ().
B
jj
j
B
yFy
π
=
∑
(3.124)
So, from the result (1.60), we obtain
()
0
0
( ) ( ) (1 ) ( ) , 1,..., ,
() 1 (),
.
u
n
i
n
B
jj
j
B
jj
j
uu Btdti m
Bt F t
φφ λβ
π
βπη
∞
=
==− =
=−
=
∑
∫
∑
∑
(3.125)
For the stationary model, we get from relation (3.121) that:
() ().
s
uu
φφ
= (3.126)
3.5.4.2 The P/SM '(0) model
The P/SM ' (0) model is the particular SM '(0)/SM '(0) model for which (3.122)
still holds.
By relation (3.101), we know that the function
i
φ
is still given by the expression
(3.125) and that for the non-ruin probabilities, we have result (3.102),
() ( ) (), 1,...,
u
ii
uuzdFzim
φφ
++
−∞
=− =
∫
(3.127)
with, by (3.99):
Insurance risk models 329
0
( ) ( ) , 1,..., , .
B
ii
Fz F ze d i mz
λξ
λξ ξ
+∞
−
=+=∈
∫
(3.128)
3.6 The M
'
/SM Model
3.6.1 General solution
Let us recall that for this model, we have:
0, 0,
() () (),, .
1,0,
j
AB
ij ij j
x
x
F
xFyByijI
ex
λ
−
≤
⎧
⎪
==∈
⎨
−≥
⎪
⎩
(3.129)
Let us first verify that the process
1
(( , , ,), 0)
nnn
JXYn
+
≥ is an SMRP satisfying
the assumption of conditional independence. Indeed, we may write that
1
(,,(,,),,) ()().
A
nnn n klkk
PJ lX xY y J X Y nJ k p F xB y
ννν
ν
+
=≤≤ ≤== (3.130)
Now let
( ), 1,...,
i
ui m
φ
= be the non-ruin probabilities related to the process
1
(( , , ,), 0)
nnn
JXYn
+
≥ starting with
1
J
i
=
.
It is clear that the probabilities we want to know, ( ), 1,...,
i
ui m
φ
=
, are given by:
1
( ) ( ), 1,..., .
m
iijj
j
upuim
φφ
=
==
∑
(3.131)
So, it suffices to know the non-ruin probabilities
( ), 1,...,
i
ui m
φ
= .
Using a reasoning similar to that used for the M/SM(0) model, we get:
00
1
() ( ) (), .
i
m
u
iiji j i
j
uped uxdBxiI
τ
λτ
φλτφτ
∞+
−
=
=+−∈
∑
∫∫
(3.132)
These relations are obtained by conditioning with the occurrence of the first
claim that occurs in (t,t+dt) and of type j.
Using the change of variables u
τ
ξ
+
= , we get:
()
0
1
() ( ) (), .
i
m
u
iiji ji
u
j
uped xdBxiI
ξ
λξ
φλξφξ
∞
−−
=
=−∈
∑
∫∫
(3.133)
These last relations show that the non-ruin probabilities
i
φ
are differentiable and
that:
'
0
1
() () ( ) (), .
m
iiiiijj i
j
uu p xdBxiI
ξ
φλφλ φξ
=
=− − ∈
∑
∫
(3.134)
This system is similar to (3.106) and here too, to simplify, let us suppose that the
d.f.
j
B
are differentiable with
j
b as derivative; then, taking Laplace transforms of
both members of this relation, we get (using notation introduced in Chapter 2,
section 5.1):
330 Chapter 7
1
() (0) () () (), ,
m
ii ii iijji
j
s
sspsbsiI
φφ λφλ φ
=
−= − ∈
∑
(3.135)
or
1
() (())()(0),.
m
iiijjijji
j
s
spbssiI
φλ δφφ
=
+−=∈
∑
(3.136)
With the following matrix notation:
() (), , () (),
iijj iij iji
s
pb s s b s
λλδδ
⎡⎤ ⎡⎤
⎡⎤
===
⎣⎦
⎣⎦ ⎣⎦
N Λ b
(3.137)
and with
()
s
φ
and
()t
φ
representing respectively the column vectors of the
functions
( ), 1,...,
i
s
im
φ
=
and (), 1,...,
i
ti m
φ
= , the last relation may be written in
the form:
()(0),s
φφφ
+− =N Λ
(3.138)
and as
,=N ΛbP
(3.139)
we get:
()
(0).s
s
φφ
⎛⎞
−
−=
⎜⎟
⎝⎠
IbP
I Λ
(3.140)
As in section 3.4, with the matrix norm defined as the sum of the absolute values
of all its elements, the norm of the matrix
()
s
A
defined as
1
() ( () )
s
s
s
=−A Λ Ib P
(3.141)
is strictly inferior to 1 for s sufficiently large as a result of the fact that
lim ( ) .
s
s
→∞
=
A0
(3.142)
Consequently, for such values of s,
()
s
−IA
is invertible and moreover
()
1
0
(()) ().
n
n
s
s
∞
−
=
−=
∑
IA A
(3.143)
By the inverse Laplace transform, relation (3.141) gives the value of the matrix
A:
() ( () )tt
=
−A Λ IB P (3.144)
where
B(t) is the diagonal matrix
0
() () ,
() ( ) , 1,..., .
ij j
t
jj
tBt
B
tbzdzj m
δ
⎡⎤
=
⎣⎦
==
∫
B
(3.145)
By the inverse Laplace transform again, from relations (3.142), (3.144) and
(3.143), we find a theoretical explicit expression for the vector
,
φ
Insurance risk models 331
()
0
0
1
()
0
0
() () (0),
(0) ( )
u
n
nj
u
n
nj
utdt
tdt
φφ
φ
∞
=
−
∞
=
⎛⎞
=
⎜⎟
⎝⎠
⎛⎞
=
⎜⎟
⎝⎠
∑
∫
∑
∫
A
A1
(3.146)
where 1is the m-dimensional vector with all components equal to 1 as
lim ( ) .
u
u
φ
→∞
=
1 (3.147)
Together with relation (3.130), relations (3.147) are formally equivalent to
relations (3.118) for the M/SM(0) model for giving the explicit form of ruin
probabilities for the M ' /SM(0) model. The difference between these two models
appears in the definitions of the matrices A and A
given by relations (3.118) and
(3.144).
The non-ruin probabilities for the model M/SM(0) and the non-ruin probabilities
( ), 1,...,
i
ui m
φ
= for the model M '/SM(0) are equal if the matrices P and B(t)
commute for all positive t which is certainly true for m=1. For m>1, P and B(t)
commute for all positive t iff functions ,
ij
B
B are identical whenever 0
ij
p > , i.e.
whenever states i and j communicate in one step in the embedded MC of the
types of claims.
Remark 3.5
(i) For the stationary model introduced in section 3.2, we know from relation
(3.68) that
'
'''
1
0
'
0
1
() ( ) ().
l
uz
z
s
lll l l
ll
kk
k
upedzuzxdBx
λ
φπφ
πλ
∞
+
−
−
=+−
∑∑
∫∫
∑
(3.148)
From relations (3.131) and (3.133), we get
0
0
() ( ) ()
i
uz
z
ii i i
uedzuzxdBx
λ
φλ φ
∞
+
−
=+−
∫∫
(3.149)
which are inverse relations of (3.131).
Using these relations in (3.148), we get the relation analogous to (3.120),
'
'
1
'
'
1
'' '
'
1
()
1
()
()
.
s
l
lll
ll
kk l
k
ll l
l
kk
k
u
up
u
φ
φπ
π
λλ
πλ φ
πλ
−
−
−
=
=
∑∑
∑
∑
∑
(3.150)
(ii) If
1,c ≠
it suffices to replace in the above formulas,
i
λ
by / , 1,..., .
i
ci m
λ
=

332 Chapter 7
3.6.2 Particular cases: the M/M and M ' /M models
3.6.2.1 The M/M model
The M/M model is the particular M/SM model for which:
0, 0,
()
1,0.
j
B
y
j
y
Fy
ey
β
−
≤
⎧
⎪
=
⎨
⎪
−
≥
⎩
(3.151)
In this case, Janssen and Reinhard (1985) proved that the non-ruin probabilities
,1,...,
i
im
φ
= can be written in the form:
0
( ) ( ) , 0, 1,...,
i
t
iijij
j
upeLutdtuim
λ
φλ
∞
−
=+≥=
∑
∫
(3.152)
where the functions
j
L are solutions of the differential system:
"1'
() ( ) () ( () ()) 0,
(0) 0, ( ) 1, 1,..., , 0.
j
jjjj j jkk
k
j
jj
Lu Lu Lu pLu
LL jmu
λ
βλ
β
−
+− − − =
=∞== ≥
∑
(3.153)
For m=2, they give the following explicit form:
12
12
() 1 , 1,2
jj
ku k u
jjj
ueej
φαα
=− − = (3.154)
with an explicit form of the coefficients.
3.6.2.2 The M '/M model
Here too, the M ' /M model is the particular M ' /SM model for which:
0, 0,
()
1,0.
j
B
y
j
y
Fy
ey
β
−
≤
⎧
⎪
=
⎨
⎪
−
≥
⎩
(3.155)
Here, relations (3.123) become:
'
0
() () () , .
j
uz
u
b
i
iii ijj
j
j
uu pzedziI
b
λ
φλφ φ
−
−
=− ∈
∑
∫
(3.156)
It follows that the functions
, 1,...,
i
im
φ
= are twice differentiable and that:
]
"'
2
0
''
11
() () () ()
1
() () () (), .
j
uz
u
b
iiiiij j j
j
jj
i
ii ii i ij j
j
ji
uup zedzu
bb
uuupuiI
bb
φλφλ φ φ
λ
λφ λφ φ φ
−
−
⎡
=− − +
⎢
⎢
⎣
⎡⎤
=− −− ∈
⎣⎦
∑
∫
∑
(3.157)
Consequently, the functions
, 1,...,
i
im
φ
= satisfy the following differential system
of order 2:
Insurance risk models 333
"'
1
() ( ) () () (), .
ii
iii i ijj
j
jii
uuupuiI
bbb
λ
λ
φλφ φ φ
=− + − ∈
∑
(3.158)
For m=1, we recover the differential equation
1
"( ) '( )uu
b
φλφ
⎛⎞
=−
⎜⎟
⎝⎠
(3.159)
discussed in Gerber (1979).
As initial conditions, we have from (3.156)
'
lim ( ) 1,
(0) (0), 1,..., .
i
u
iii
u
im
φ
φλφ
→∞
=
==
(3.160)
The interest of result (3.158) lies in the possibility it provides of stating the
general solution as a linear combination of negative exponential functions, as in
(3.154), usually with constant coefficients, which is always interesting from a
numerical point of view.
Remark 3.6
Concerning the numerical point of view, Reinhard and Snoussi
(2002) give another approach using a discrete time scale and recursive algorithms
to obtain the joint distribution of the surplus prior to ruin and to compute the
severity of ruin.
Nevertheless, let us mention that a prudent attitude of the insurance companies
implies that the use of the non-ruin probability on an infinite time horizon is the
best criteria and of course does not need to use the severity of ruin.
Chapter 8
RELIABILITY AND CREDIT RISK MODELS
In this chapter, the reader will first find a short summary of the basic notions of
reliability and then the semi-Markov extensions.
After that, the classical problem of credit risk is also presented together with an
analogy with reliability and it is shown how semi-Markov models are useful for
this important topic of finance in connection with the new rules of the Basel
Committee.
1 CLASSICAL RELIABILITY THEORY
Reliability theory is mainly concerned with the security of material fittings.
A first distinction must be made between simple and complex structures.
For a simple structure, it is possible to define what is called the lifetime of the
considered system, defined as the r.v. T representing the time interval between
time 0 and the time of the first failure, failure meaning that the system is out.
A complex system is composed of several simple components, from which
failures have an impact, more or less important, on the way the system is
working.
1.1 Basic Concepts
Let us consider a simple structure called the reliability system S having r.v. T as
lifetime, T being defined on the probability space
(
)
,,PΩℑ .
Definition 1.1 The reliability function of S is given by the function U defined as
[
)
() ( ), 0, .Ut PT t t
=
>∈∞ (1.1)
U(t) represents the probability that no failure happens before t. If F represents the
distribution function of T, it is clear that for all non-negative t:
U(t)=1
−
F(t). (1.2)
If the density function f of T exists, we obtain:
() ( ) .
t
Ut fudu
∞
=
∫
(1.3)
From now on, we always assume that the f or the derivative of U exists.
Definition 1.2 The function r, defined as

336 Chapter 8
() '()
() , 0,
1() ()
ft U t
rt t
Ft Ut
⎛⎞
==− >
⎜⎟
−
⎝⎠
(1.4)
is called the failure rate of the component.
Its meaning is simple: let us consider a time t such that the event {T>t} occurs.
From basic definitions of conditional probability (relation (6.4) of Chapter 1) and
from relation (1.2), we can successively write:
()
(
)
()
()
()
'( )
()
() .
Pt T t dt
PT t dtT t
PT t
ftdt
Ut
Ut
dt
Ut
rtdt
<≤+
≤+ > =
>
=
=−
=
(1.5)
Consequently, r(t)dt simply represents the conditional probability of having a
failure in the infinitesimal time interval (t,t+dt) given that the component has no
failure before or at time t. So, the value of the failure rate at time t is a risk
measure to have suddenly a failure just after time t.
By integration, relation (1.4) gives:
0
()
()
t
rudu
Ut e
−
∫
= (1.6)
provided that we suppose that U(0)=1.
From the last relation, it is clear that any non-negative function can be a failure
rate if the following two conditions are satisfied:
- the function r is integrable on the positive half real line,
-
0
() .rudu
∞
=
∞
∫
(1.7)
The mean lifetime
T is just the mean for the d.f. F.
By integration by parts, it is possible to show that
0
()TUtdt
∞
=
∫
(1.8)
and similarly if the variance
2
σ
exists:
2
0
2()tU t dt
σ
∞
=
∫
(1.9)
1.2 Classification Of Failure Rates
The first classification of failure rate types was given by Barlow and Proschan
(1965) with the following definition.

Reliability and credit risk models 337
Definition 1.3 There are three types of failure rates:
(i) increasing failure rate type (in short IFR) iff
12 1 2 1 2
,: () ()tt t t rt rt∀<⇒<, (1.10)
(ii)
decreasing failure rate type (in short DFR) iff
12 1 2 1 2
,: () ()tt t t rt rt∀<⇒>, (1.11)
(iii) constant failure rate type (in short CFR) iff
12 1 2 1 2
,: () ()tt t t rt rt∀<⇒=. (1.12)
In the last case, let us write ( )rt
λ
=
; then relation (1.6) gives:
() , 0
t
Ut e t
λ
−
=
≥ (1.13)
so that the d.f. of T is the negative exponential distribution of parameter
λ
(see
Chapter 1, section 5.5).
Later Barlow and Prochan (1965) refine this classification with the following
definition.
Definition 1.4 (i) A failure rate is of increasing failure rate average (in short IFRA) type
(respectively of decreasing failure rate average (in short DFRA) type) iff the function
[
)
0
1
() , 0,
x
xrtdtx
x
∈∞
∫
is increasing (respectively decreasing).
(ii) A failure rate is of new better than used (in short NBU) type (respectively of
old better than used (in short OBU) type) iff
()()()(),,0.Ux y UxUy xy+≤≥ ∀ > (1.14)
The meaning of these last two types is simple; for the OBU type, for example, we
can write inequality (1.13) in the form:
()
()
()
Ux y
Ux
Uy
+
≥ (1.15)
or
()
()
()
PT x y
PT x
PT y
>+
>≥
>
(1.16)
and finally
()( ),PT x PT x yT y>≥ >+ > (1.17)
this last relation meaning that, given the event {T>y}, the conditional probability
of the event {T>x+y} is always smaller than the unconditional probability of the
same event for y=0. In other terms, the fact of working up to time x always
implies a wear phenomenon called aging.
Let us mention that it is possible to show (Barlow and Proschan (1965)) that the
following inclusions are true:
,
.
IFR IFRA NBU
D
FR DFRA OBN
⊂⊂
⊂⊂
338 Chapter 8
Moreover, these inclusions are strict.
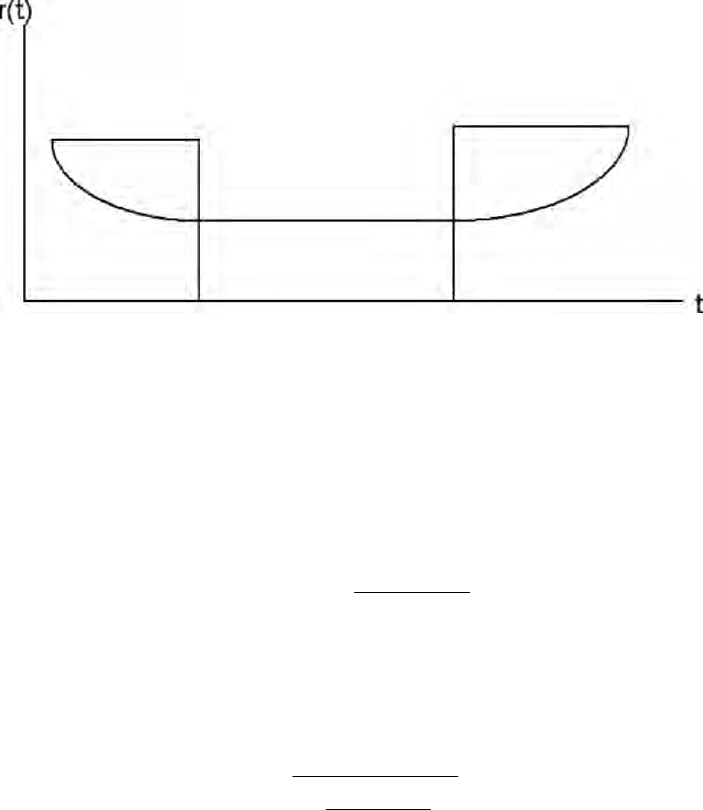
The general shape of a failure rate is the “bathtub” with three periods: in the
beginning, it is of type DFR, then there is a time interval in which it is of
exponential type and finally in a third and later period, of IFR type:
Figure 1.1: “Bathtub” shape of a failure rate
1.3 Main Distributions Used In Reliability
Referring to section 5 of Chapter 1, we will give the principal distributions used
in reliability theory, together with the value of the failure rate and its type, if any.
(i) Poisson distribution of parameter
λ
;
(ii) Gamma distribution
1
1
(,), () ;
rt
ru
t
te
rrt
ue du
λ
λ
γλ
−−
∞
−−
=
∫
(1.18)
(iii) Weibull distribution of parameters , ,
λ
β
()
1
()rt t
β
λβ λ
−
=
( 1: , 1: , 1:IFR DFR EXP
β
ββ
>< =); (1.19)
(iv) log-normal distribution of parameters , ,
μ
σ
22
22
(ln ) / 2
(ln ) / 2
() ;
t
u
t
e
rt
e
tdu
u
μσ
μσ
−−
−−
∞
=
∫
(1.20)
(v) the truncated normal law of parameter ( , )
μ
σ
for which the density is
defined as
