Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability

Reliability and credit risk models 339

2

()

2

()

0

2

11

() ' ,

2

1

,

2

t

ft e

k

kedt

μ

σ

μ

σ

μ

σσ

σπ

μ

σ

σπ

−

−∞

⎛⎞

−

⎛⎞

==Φ

⎜⎟

⎝⎠

⎛⎞

==Φ−

⎜⎟

⎝⎠

∫

(1.21)

Φ being defined in Chapter 1 as the distribution function of an N(0,1) r.v.

The failure rate has the value

2

()

2

()

2

'

() .

t

e

rt

t

edu

μ

σ

μ

σ

μ

σ

μ

σ

−

∞

⎛⎞

−

⎛⎞

Φ

⎜⎟⎜⎟

⎝⎠

⎜⎟

==

−

⎛⎞⎜⎟

Φ

⎜⎟

⎝⎠

∫

(1.22)

1.4 Basic Indicators Of Reliability

Generally speaking, let us suppose now that the considered component is

repairable, that is to say that if there is a failure at time t, we can repair the

component using a random time Y and that after reparation, the component will

start again with the same failure rate as before the reparation. This is the concept

of minimal reparation.

The distribution function G of the repair time Y is called the maintainability

function and the equivalent of the failure rate the repair rate function noted s, so

that:

0

()

'( )

() ,

1()

() 1 .

t

s

udu

Gt

st

Gt

Gt e

−

=

−

∫

=−

(1.23)

The effect of considering possible reparations implies that we can now introduce

a two-state system with as state space

{

}

0,1 , these two states representing

respectively working and repair states.

Now the reliability system can have transition from one state to the other one: at

time 0, the system is in the operating state or state 1 or up state; at the time of the

first failure

1

T , it goes into state 0 or down state for a time

1

Y and so on.

The time evolution of the system S is thus theoretically given by the sequence

{

}

11

, ,..., , ,...

nn

TY T Y and from now on, let Z(t) represent the state of the considered

system at time t.

Definition 1.5

The basic indicators of reliability are:

(i) the mean time to failure (MTTF) :MTTF=E(T),

(ii) the mean time to repair (MTTR):MTTR=E(Y),

340 Chapter 8

(iii) the point-wise (or instantaneous) availability: (() 1)PZt

=

,

(iv) the steady-state availability:

lim ( ( ) 1)

t

APZt

→∞

=

= ,

(v) the average availability on the interval [t,t+u]:

1

(, ) ( ) ,

tu

t

Att u Audu

u

+

+=

∫

(1.24)

(vi) the limit average availability on the interval [t,t+u]:

0

1

(, ) lim ( ) .

t

Att u Audu

t

→∞

+=

∫

(1.25)

1.5 Complex and Coherent Structures

In general, a structure is composed of several simple components and the event

failure of this complex structure depends on the way these components are

working. Theoretically, this is given with the so-called structure function.

Let us suppose that all the n components of the complex structure C are simple,

so that, for each i=1,…,n,

1, (operating or up state),

()

0, (failed or down state).

ii

xxt

⎧

==

⎨

⎩

(1.26)

The state x of the structure C at time t, is given by

1

1, ( up state),

( ) ( ( ), , ( ))

0, (down state),

n

xt x t x t

ψ

⎧

==

⎨

⎩

… (1.27)

where the function

{} {}

:0,1 0,1

n

ψ

 (1.28)

is called the structure function of C.

Let us now give the following definitions.

Definition 1.6 The complex component has a monotone structure iff

11

, (,,) (,,), 1,,,

(0, ,0) 0, (1, ,1) 1.

ii n n

x

yxxyyin

ψ

ψψ

≤⇒ ≤ =

==

………

……

(1.29)

Definition 1.7

A component i (i=1,...,n) of a complex system is irrelevant iff the

structure function is constant in

i

x

; otherwise, this component is called relevant.

Definition 1.8

The complex component has a coherent structure iff it is

monotone and each component is relevant.

Particular cases

(i) A series structure functions iff each component does.

(ii) A parallel structure functions if at least one component does.

Reliability and credit risk models 341

(iii) A k-out-of n structure functions iff at least k of the n components function.

For these three types of structure, the structure functions are successively given

by:

(i)

()

(

)

1

1,...,

1

,..., min ,

n

ni i

in

i

x

xx x

ψ

=

==

∏

(1.30)

(ii)

()

(

)

1

1,...,

1

,..., max ,

n

ni i

in

i

x

xx x

ψ

=

==



(1.31)

(iii)

()

1

1, ,

,...,

0, .

n

i

n

i

x

k

xx

x

k

ψ

=

⎧

≥

⎪

=

⎨

⎪

<

⎪

⎩

∑

(1.32)

Remarks 1.1 (i) Barlow and Proschan (1965) have proved that for any coherent

structure, we have the intuitive result

()

1

,..., .

n

ini

i

x

xx x

ψ

=

≤≤

∏



(1.33)

(ii) If all the components are independent and if

( 1,..., )

i

Ui n

=

is the reliability

function of component i, then, we have for a series system:

1

() (),

n

i

Ut Ut

ψ

=

∏

(1.34)

for a parallel system:

1

() 1 (1 ()),

n

i

Ut Ut

ψ

=

=− −

∏

(1.35)

and for a k-out-of n system:

( ) ( ( )) (1 ( )) ( for ( ) ( ), 1,..., ).

n

ini

i

ik

n

U t Ut Ut U t Ut i n

i

ψ

−

=

⎛⎞

=− ==

⎜⎟

⎝⎠

∑

(1.36)

Example 1.1

Let us consider a complex system for which component i (i=1,…,n)

has a negative exponential distribution of parameter ( 1,..., )

i

in

λ

=

.

If the structure is a series structure, it follows from result (1.34) that:

1

()

n

i

t

n

t

i

Ut e e

λ

ψ

=

⎛⎞

⎜⎟

−

⎜⎟

−

⎝⎠

=

⎛⎞

∑

⎜⎟

==

⎜⎟

⎝⎠

∏

(1.37)

342 Chapter 8

and so, this structure has also a negative exponential distribution whose

parameter

1

n

i

λ

=

∑

.

Moreover as

1

, 1,..., ,

i

Ti n

λ

==

(1.38)

we have:

1

11

,

n

i

TT

=

∑

(1.39)

a result showing that MTTF for the complex structure is given by the harmonic

mean of the MTTF of all the n components.

If all the components have the same reliability function, this last result gives:

1

.

T

n

= (1.40)

Example 1.2

Let us consider the redundant structure formed by a complex

structure composed of n identical components in parallel, all having a negative

exponential reliability function of parameter

λ

. From result (1.35), we get:

() 1 (1 ),

tn

Ut e

λ

ψ

−

=− − (1.41)

and so from relation (1.4):

1

(1 )

() ,

1(1 )

tn

t

tn

e

rt ne

e

λ

ψ

λ

−−

−

=

−−

(1.42)

proving that here the failure rate is time dependent.

It is not difficult to show that:

1

1(),

0()(),

1

() .

1

n

t

nrt

trtnt

ne

trt

e

ψ

λ

ψ

λ

λλ

λ

−

>⇒ <

→⇒

−

→∞⇒ →

−

∼

(1.43)

These last results show the effect of redundancy, which adds to a simple negative

exponential component, n

−1 supplementary components in parallel to improve

the reliability.

This effect is important at the beginning and of course is time decreasing with

time t to converge to

λ

.

For the MTTF, we have that:

1

,

n

k

TT

k

ψ

=

∑

(1.44)

Reliability and credit risk models 343

and so the ratios of the MTTF are given for example by :

N

1 2 3 4

MTTF ratio 1 1.5 1.83 2.08

Table 1.1: example of MTTF

This clearly shows that the effect of redundancy is not proportional to the number

of added components.

2. STOCHASTIC MODELLING IN RELIABILITY

THEORY

2.1 Maintenance Systems

In the last subsection, result (1.34) shows that for a series structure, the reliability

function is highly decreasing with the number of components.

However, if the components are repairable, it is possible to interrupt the system

momentarily during the reparation of the failed component and then to reinsert

the component in the system and so on.

For such a possibility, one can construct a stochastic model (Mohan et al (1962))

to compute the main indicators given in section 1.4.

Let us assume that all the n components are independent with negative

exponential distributions, respectively with parameters

1

,...,

n

λ

, and that the

repair time for component i (i=1,…,n) has a negative exponential distribution of

parameter

i

μ

. All the repair times are also independent and of other and of on the

working times of the n components.

Moreover there is no time loss to replace the repaired components in the system.

The evolution of the system can be seen as a successive sequence of working and

repair times.

For example for n=1, the random sequence

(

)

11 2 2

, , , ,..., , ,...

nn

XYXY X Y (2.1)

represents successively the working and repair times and if we introduce a two-

state set {0,1}, so that, at time t, the system state Z(t) is in state 1 if it is operating

and in state 0 if it is under repair, then the process (2.1) is a continuous Markov

process where the transition matrix of the imbedded Markov chain is given by:

01

10

⎡

⎤

⎢

⎥

⎣

⎦

(2.2)

and for which the conditional sojourn times are given by:

344 Chapter 8

10

01

0, 0,

10:()

1,0,

0, 0,

01:()

1,0.

t

Ft

et

t

Ft

et

λ

μ

−

<

⎧

=

⎨

−

≥

⎩

<

⎧

=

⎨

−

≥

⎩



(2.3)

With the notation of Chapter 3, we have here:

10 1 01 0

11

,,bb

ηη

λ

μ

== == (2.4)

and for the stationary distribution of the imbedded Markov chain:

01

1

.

2

ππ

=

= (2.5)

We are interested in the following two transition probabilities:

10

01

() ( () 0 (0) 1),

() ( () 1 (0) 0).

tPZt Z

φ

=

==

=

==

(2.6)

They are given by the system (10.3) of Chapter 4.

For n=2, using Laplace transforms, it is possible to show that

()

10

()

01

() (1 ),

() .

t

te

λμ

λ

φ

λμ

μμ

φ

λμ λμ

−+

=−

+

=+

++

(2.7)

The asymptotic behaviour is given by relation (10.8) of Chapter 3, or here

directly from result (2.7),

10

01

lim ( ) ,

lim ( ) .

t

λ

φ

λ

μ

φ

λ

μ

→∞

=

+

=

+

(2.8)

As here, we have:

11

,,MTTF MTTR

λ

μ

== (2.9)

relations (2.8) take the form

10

01

lim ( ) ,

lim ( ) .

t

MTTR

t

M

TTF MTTR

MTBF

t

M

TTF MTTR

φ

→∞

=

+

=

+

(2.10)

Remark 2.1

a) Mohan et al (1962) also solved the case of a series system with n

components, independent with negative exponential distributions, respectively

Reliability and credit risk models 345

with parameters

1

,,

n

λ

… , and that the repair time for component i (i=1,…,n) has

a negative exponential distribution of parameter

μ

.

In terms of semi-Markov modelling, this means that the state process

(

)

(), 0Zt t≥ has as state space the set {1,…,n,Op} where state i (i=1,…,n), means

that the system is in the failure state due to component i, and state Op that the

system is operating at time t.

With the same semi-Markov approach, it is possible to show that:

()

0

1

( ) (1 ), 1,..., ,

() ,

()( 1 ()) ,

.

t

i

t

Op

t

Op

n

tein

e

t

e

tt

λμ

λ

φ

λμ

μλ

φ

λμ

λλ

φφ

λμ

λλ λ

−+

=− =

+

=

+

−

=− =

+

=++



(2.11)

And consequently, the asymptotic behaviour is given by the following relations:

()

0

lim ( ) , 1,..., ,

lim ( ) ,

() .

i

t

Op

t

tin

e

t

λμ

λ

φ

λμ

μλ

φ

λμ

λ

φ

λμ

→∞

−+

→∞

==

+

=

+

=

+

(2.12)

b) For the general stochastic model of Mohan et al (1962), there exists a simple

form of the asymptotic behaviour given by the following expressions:

1

0

1

lim ( ) , 1,..., ,

1

lim ( ) ,

1

() .

1

i

n

t

i

Op

n

t

i

n

i

n

i

tin

t

λ

φ

λ

μ

φ

λ

μ

λ

μ

φ

λ

μ

→∞

=

→∞

=

==

+

=

+

=

+

∑

(2.13)

346 Chapter 8

2.2. The Semi-Markov Model For Maintenance Systems

Let us consider a complex system having as state space the set I={1,…,m} with

m finite.

The set I is partitioned in two non-void subsets U and D where U is the set of all

functioning or up states and D all the failed or down states and at any time t, the

considered system is in one of these states and transitions are of course possible.

Any duration in one of the states of U is an operating time and any duration in a

state of D a non-operating time; a transition from a state of U to a state of D

means that there is a breakdown and a transition from a state of D to a state of U

may be seen as the end of a time of reparation.

The basic assumption is that the process

{

}

(), 0ZZtt

=

≥ is a semi-Markov

process with kernel Q.

As in section 2.1, the minimal case is considered with the semi-Markov process

with

{

}

0,1I = where state 0 means breakdown state and state 1 operating state.

As before the main reliability indicators are:

(i) The availability functions defined as:

(

)

()

() () (0) , ,

(,) () () , ,

i

At PZt UZ i i I

Ast PZt UZs i i I

=∈=∈

=

∈=∈

(2.14)

respectively in the homogeneous and the non-homogeneous case.

If as in Chapter 3, we define by

ij

φ

the transition probability functions for the Z-

process, for both the cases, we get:

() (), ,

(,) (,), .

iij

jU

iij

jU

At t i I

Ast st i I

φ

∈

=∈

=

∈

∑

(2.15)

If, in the homogeneous case, the process is ergodic, we can also define the

asymptotic availability as:

() lim () .

jj

ii

t

jU

kk

kI

AAt

π

η

π

η

→∞

∈

∞= =

∑

(2.16)

(ii) The reliability functions giving the probability that the system is always

working on the time interval [0,t],

() ( () (0) ), ,

(,) ( () () ), .

i

Rt PZt UZ i i U

R

st PZt UZ s i i U

=∈ =∈

(2.17)

Reliability and credit risk models 347

To compute these probabilities, we will now work with another kernel

D

Q

for

which all the states of the subset D are changed into absorbing states, meaning

that:

,,,

() , , ,

D

ij ij

D

ij ij

piDjI

p

siDjI

δ

=∈∈

=

∈∈

(2.18)

respectively for the homogeneous and the non-homogeneous case.

Doing so, in the two cases, we get:

() (), ,

(,) (,), ,

D

iij

jU

D

iij

jU

Rt t i U

R

st st i U

φ

∈

=∈

∑

(2.19)

where of course, in both the homogeneous and the non-homogeneous cases, the

matrix

D

Φ gives the probabilities transition for the semi-Markov process of

kernel

D

Q .

(iii) the maintainability functions giving the probability that the system is down

at time 0 in the homogeneous case and at time s in the non-homogeneous case

and that the system will leave the set D within the time t,

(

]

(

)

(

]

()

() 1 ( ) , 0, ,

(,) 1 () , , .

Mt PZu D u t

M

st P Zu D u st

=− ∈ ∀∈

(2.20)

To compute these probabilities, we will now work with another kernel

U

Q for

which all the states of the subset U are changed in absorbing states, meaning that:

,,,

() , , .

U

ij ij

U

ij ij

p

iUj I

p

siUjI

δ

=∈∈

=

∈∈

(2.21)

Doing so, respectively, we get:

() (), ,

(,) (,), ,

U

iij

jU

U

iij

jU

Mt ti D

M

st st i D

φ

∈

=∈

∑

(2.22)

where of course, the matrix

U

Φ gives the probabilities transition for the semi-

Markov process of kernel

U

Q .

In conclusion, we see that the computing of the main indicators for the semi-

Markov model is simple from our numerical results given before.

348 Chapter 8

2.3 A Classical Example

In this part the example given in Barlow and Proschan (1965) page 120 will be

developed. It is supposed that there are two machines (computers in the original

example) working in parallel. The system is formed by nine states. With three of

these states

{

}

5,7,9D = the system is down, in the other six the system can

work.

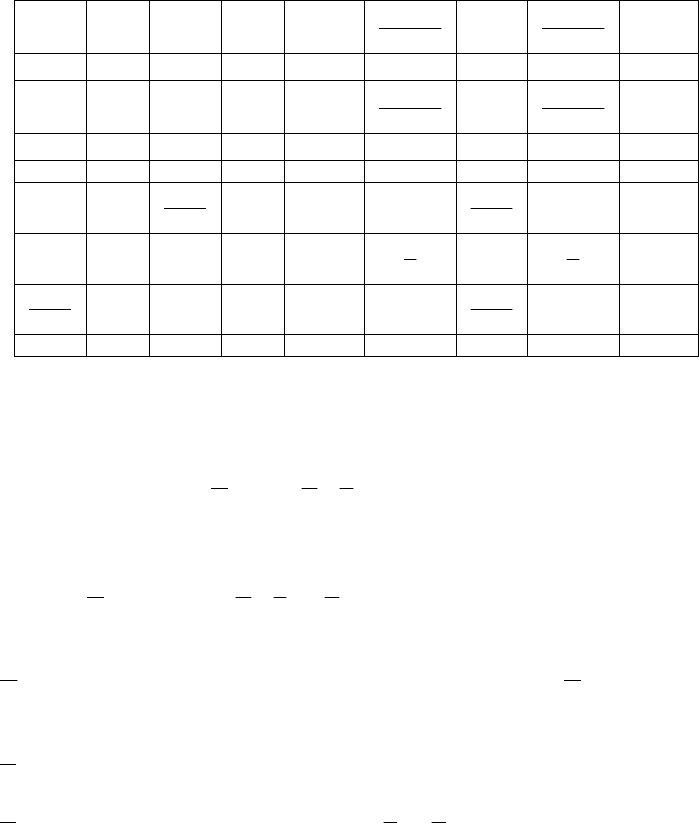
The MC that describes the system is given in

Table 2.1.

0

2 t

e

λ

−

0 0 0

0

2

1

2

t

e

λ

−

0

2

1

2

t

e

λ

−

0

0 0

e

λ

γ

−

0 0 0 0 0

1 e

λ

γ

−

0 0 0

0

2 t

e

λ

−

0

2

1

2

t

e

λ

−

0

2

1

2

t

e

λ

−

0

e

λ

γ

−

0 0 0

1 e

λ

γ

−

0 0 0 0

0 0 0 0 0 1 0 0 0

0 0

θ

λ

θ

+

0 0 0

λ

θ

+

0 0

0 0 0 0 0

1

2

0

1

2

0

θ

λ

θ

+

0 0 0 0 0

λ

θ

+

0 0

0 0 0 0 0 0 0 1 0

Table 2.1: embedded MC

The embedded MC for the homogeneous case is the same as in

Table 2.1 and

with parameter values:

1

35

λ

=

;

11

6

θ

=

; 1

γ

=

;

0

24t

=

. (2.23)

In the non-homogeneous case the parameters are functions of time; more

precisely:

1

40, ,30

λ

= …

;

11 1

,,

84

θ

= 

; 0.4, ,1.2

γ

=

… ;

0

30, ,20t

=

… (2.24)

where:

1

λ

is the mean time to failure. In the non-homogeneous case,

1

λ

is a decreasing

function of the time in the sense that it goes from 40 to 30 in 11 steps.

1

θ

is the mean time to perform emergency repair. In the non-homogeneous case

1

θ

is an increasing function that goes from

11

to

84

in 11 steps.

Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability

Подождите немного. Документ загружается.