Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability
Подождите немного. Документ загружается.


198 Chapter 5
Solution
Yearly vol.
0.12
Maturity.
0.08219
r=ln(1+i)
0.076962
Results call put
Price 3.04721 0.42926
Delta 0.7847 -0.2153
Vega 8.3826 idem
Theta 11.924 4.334
Gamma 0.08499 idem
Rhô 6.199 -1.805
Table 6.1: example option computation
7 THE IMPACT OF DIVIDEND DISTRIBUTION
If between t and T, the asset distributes N dividends of amounts
1
,...,
N
DD at
times:
12
(0 ) ( )
N
ttt t T
<
<<<< < , (7.1)
the impact of the value of a European call is the following : as the buyer of the
call cannot receive these dividends, it suffices to compute the present value at
time t of these dividends and to subtract the sum from the asset value at time t so
that the call value is now:
.,...,1,
),,(),...,;,(
1
1
Njtt
eDSCDDSC
jj
N
j
jN
j
r
=−=
−=
−
∑
=
τ
ττ
τ
(7.2)
Of course, the most usual case is N=1.
If we assume that the distribution of dividends is given with a continuous payout
at rate D per unit of time,
0
tT
t' t'+dt'
Ddt'
Figure 7.1: continuous "payout"
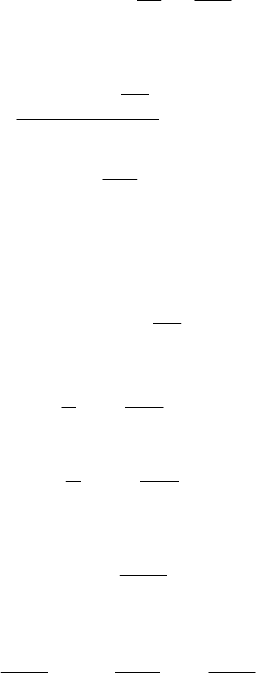
Black & Scholes extensions 199
the capitalised value is
D
e
τ
and so the value of the call is given by:
(,; ) ( ,).
Dt
CS D CSe
τ
τ
−
=
(7.3)
8 ESTIMATION OF THE VOLATILITY
8.1 Historic Method
This method is based on the data of the underlying asset evolution in the past, for
example the n daily values
(
)
n
SSS ,...,
10
. (8.1)
Let us consider the following sample of the consecutive ratios:
()
1
1
01
,..., ,..., .
n
n
n
S
S
RR
SS
−
⎛⎞
=
⎜⎟
⎝⎠
(8.2)
From the log-normal distribution property, we have:
2
1
ln ( )
2
(0,1),
with , 1,..., .
t
t
t
t
R
N
S
R
tn
S
σ
μ
σ
−
−−
==
(8.3)
It follows that the random sample
(
)
n
RR ln,...,ln
1
can be seen as extracted from
a normal population
()
2
',
μ
σ
with:
2
'.
2
σ
μμ
=−
(8.4)
The classical results of mathematical statistics give as best estimators:
1
1
2
2
1
1
1
ˆ
'ln,
1
ˆˆ
ln ' .
n
k
k
k
n
k
k
k
R
nR
R
nR
μ
σμ
=
−
=
−
=
⎛⎞
=−
⎜⎟
⎝⎠
∑
∑
(8.5)
To get an unbiased estimator of the variance, we have to use:
22
ˆ
1
ˆ
ˆ
σσ
−
=
n
n
(8.6)
or:
.)'
ˆ
(
1
ln
1
1
ˆ
2
2
1
1
2
μσ
−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
∑
=
−
n
n
R
R
n
n
k
k
k
(8.7)
200 Chapter 5
Example 8.1 On the basis of a sample of 27 weekly values of an asset starting
from the initial value 26.375 Euro, the following weekly estimations are found:
2
ˆ
0.016732,
ˆ
0.005216.
μ
σ
=
=
Consequently, as the parameters of the Black and Scholes model must be
evaluated on a yearly basis, we get
.
2
.
.
ˆ
52 0.016732 0.870064 0.87,
ˆ
52 0.005216 0.271232,
ˆ
0.271232 0.520799 0.52.
an
an
an
μ
σ
σ
=× = ≅
=× =
==≅
8.2 Implicit Volatility Method
This method assumes that the Black and Scholes formula calibrates the market
values of the observed calls well.
Theoretically, an inversion of the Black and Scholes formula gives the value of
the volatility
σ
.
On the basis of several observations of the calls for the same underlying asset, we
can use the least square statistical method to refine the estimation.
Example 8.2
Using the data of Excercise 6.2, we assume that we have an observed value of
the call 3.04715, but without knowing the volatility.
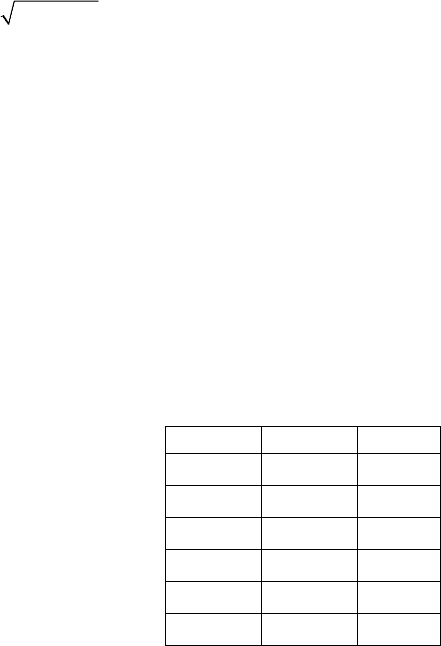
The next table gives the results using a step by step approximation method.
weekly vol.annual vol. call value
0.02 0.144 3.26
0.015 0.1081 2.95
0.017 0.1225 3.069
0.016 0.1153 3.008
0.0165 0.1189 3.038
0.01664 0.1199 3.04713
Table 8.1: volatility computation
So, we do find the correct volatility value 0.12.
Remark 8.1 The main difficulty is to select the historical data.
The set must not be too long or too short in order to avoid perturbed periods
introducing strong biases in the results.
Black & Scholes extensions 201
Moreover, we always work with the assumption of a constant volatility that we
will suppress in section 10.
9 BLACK AND SCHOLES ON THE MARKET
9.1 Empirical Studies
Since the opening of the CBOT in Chicago in 1972, numerous studies have been
carried out for testing the results of the Black and Scholes formula.
In the case of efficient markets, the conclusions are the following:
(i) the non-risky interest rate has little influence on the option values,
(ii) the Black and Scholes formula underestimates the market values for calls
with short maturity times, for calls “deep out of the money” (S/K<0.75) and for
calls with weak volatility,
(iii) the Black and Scholes formula overestimates the market values for calls
“deep in the money” (S/K<1.25) and for calls with high volatility. The put values
are often underestimated particularly in the “out of the money” (S>>K) case.
(iv) the puts are often underestimated particularly when they are out of the
money(S<<K).
9.2 Smile Effect
If we compute the volatility values with the implicit method in different times, in
general, the results show that the volatility is not constant, invalidating thus one
of the basic assumptions of the considered Black and Scholes model.
The graph of the volatility as a function of the exercise price often gives a graph
with a convex curve, a result commonly called the “smile effect”.
But sometimes, concave functions are also observed.
Although, theoretically, volatilities for the pricing of calls and puts are identical,
in practice, some differences are observed; they are assigned to differences of
“bid-offer spread” and to the methodology of the implicit method used at
different times.
The fact that it is important to consider option pricing models with non-constant
volatility is one of the motivations of the next model.
10 THE JANSSEN-MANCA MODEL
In this section, we present a new extension of the fundamental Black and Scholes
(1973) formula in stochastic finance with the introduction of a random economic

202 Chapter 5
and financial environment using Markov processes and which we owe to Janssen
and Manca (1999).
In preceding papers (Janssen et al (1995), Janssen et al (1997), Janssen et al
(1998), Janssen and Manca (2000)), these authors already show how it is useful
to introduce Markov and semi-Markov theory in finance, with the assumption
that the evolution of the asset follows a semi-Markov process, homogeneous or
non-homogeneous, and how to price options in such new models. The main idea
of this approach is to insert a strong dependence of the asset evolution as a
function of the preceding value.
The construction of this new model starts from the classical CRR model with one
period to obtain a new continuous time model satisfying the assumption of
absence of arbitrage.
One of the main potential applications of our model concerns the possibility to
get a new way of acting with the Black and Scholes formula with information
related to the economic and financial environment, particularly concerning the
volatility of the underlying asset.
This new model also gives the possibility to take into account anticipations of
investors in such a way as to incorporate them in their own option pricing.
By the same philosophy, the model can be used to construct scenarios and
particularly in the case of stress in a VaR approach.
10.1 The Markov Extension Of The One-Period CRR Model
10.1.1 The Model
Starting on a complete probability space
(
)
P,,
ℑ
Ω
, let us consider a one-period
model for the evolution of one asset having the known value
0
)0( SS
=
at time 0
and random value S(1) at time 1.
The economic and financial environment is defined with random variables
01
,
J
J
representing the environment states respectively at time 0 and time 1. These
random variables take their values in the state space
{
}
1,...,
E
m= and are defined
on the probability space by:
(
)
()
0
10
, 1,..., ;
, , 1,..., ,
i
ij
PJ i ai m
PJ J i p ij m
== =
== =
(10.1)
where:

Black & Scholes extensions 203
1
1
0, 1,..., ;
1,
0, , 1,..., ,
1, 1,..., .
i
m
i
i
ij
m
ij
j
ai m
a
p
ij m
p
im
=
=
≥=
=
≥=
==
∑
∑
(10.2)
Furthermore, let us introduce the following function of
01
,
J
J
:
01
J
J
u ,
01
J
J
d ,
01
J
J
q such that, a.s.:
01 01 01
01 01
0,
1, 1 ,
J
JJJ JJ
JJ JJ
dru
dr
<
<<
<<
(10.3)
01
01.
JJ
q
<
< (10.4)
The one-period model, related to the process
{
}
(0), (1)SS, is the following: given
01
,
J
J and that
0
(0)SS= , the asset has the following evolution: it goes up from
0
S to
01
0JJ
uS with the conditional probability
01
J
J
q or goes down from
0
S to
01
0JJ
dS with the conditional probability
01
1
J
J
q
−
; moreover, the non-risky interest
rate of this period has the value
01
J
J
ν
defined by:
01 01
1.
JJ JJ
r
ν
=
− (10.5)
Given
01
,
J
J , we have that:
(
)
()
()
()
()
()
01 01
01 01
01 01 01 01
000 0 0
0010
0010
010 0 0
00 0 0
1
00
11
(1) , , ,
(1) , , 1 ,
(1) , , (1 ) ,
(1) , ( (1 ) ),
(1) ( (1 ) )
JJ JJ
JJ JJ
JJ JJ JJ JJ
m
Jj Jj Jj Jj Jj
j
mm
ij ij ij ij ij
ij
PS u S J J S q
PS d S J J S q
ES J J S q u S q d S
ES J S p q u S q d S
E
SS PJi pqu qdS
=
==
==
==−
=+−
=+−
⎡
⎤
== +−
⎣
⎦
∑
∑∑
0
.
(10.6)
One of the basic concepts of stochastic finance is the absence of arbitrage
possibility. In fact, it is equivalent to say that the process
{
}
1
(0), (1)rS S
−
is a
martingale where 1r
ρ
=+ and
ρ
is an adequate non-risky interest rate for
computing the present value of S(1) at time 0.
Here, we must take into account the possible information of the investor
concerning the environment; at time 0, in addition to the knowledge of
0
S ,
different information sets may be available. Three cases are possible:

204 Chapter 5
1) knowledge of
(
)
01
,
J
J
In this case the martingale condition:
(
)
01
010 0
(1) , ,
JJ
E
SJJS rS=
(10.7)
becomes:
01 01 01 01 01
00 0
(1 )
JJ JJ JJ JJ JJ
rS quS q d S
=
+− (10.8)
or
01 01 01 01 01
(1 ) .
J
JJJJJ JJJJ
rqu qd
=
+− (10.9)
This last condition is exactly the same as the CRR model; this means that the
new conditional probability for which the martingale condition is satisfied is
given by:
01 01
01
01 01
J
JJJ
JJ
J
JJJ
rd
q
ud
−
=
−
. (10.10)
This value defines the so-called risk neutral conditional probability measure.
As an example of application in option pricing, let us consider that we want to
study a European call option of maturity T=1 and exercise price K bought at time
0.
It follows that at time 1 or at the end of the maturity, the value of the option will
be given by the random variable:
{
}
((1),0) max0,(1) .CS S K=− (10.11)
We compute the price of the option at time 0 with a maturity period of value 1, as
the conditional expectation under the risk neutral conditional probability
measure, denoted
01
,0
(,1)
JJ
CS, of the present value of the gain at time 1:
{
}
(
)
{} {}
01 01
01 01 01 01 01
1
,0 01
1
00
(,1) max0,(1) ,
max 0, (1 ) max 0, .
JJ JJ
JJ JJ JJ JJ JJ
CS Er S KJJ
rq uSK q dSK
−
−
=−
⎡⎤
=−+−−
⎣⎦
(10.12)
2) knowledge of
0
J
Let us begin to see what the martingale condition becomes.
We have that:
()
(
)
(
)
00 010 00
(1) , (1) , , , .
E
SJS EESJJSJS= (10.13)
As the assumption of AOA is now satisfied for the conditioning with
01
,
J
J , we
can write that
()
(
)
01
00 000
(1) , , ,
JJ
E
SJS ErSJS=
(10.14)
and so:
(
)
(
)
01
0, 0 0 0 0
(1) , , ,
JJ
E
SJS SErJS= (10.15)

Black & Scholes extensions 205
and finally:
(
)
0
0, 0 0
(1) ,
J
E
SJS S
ς
=
(10.16)
where:
000
1
m
J
JjJj
j
p
r
ς
=
=
∑
. (10.17)
These last two formulas show that, given, at time 0, the initial environment state,
the AOA is still valid with as risk neutral interest
00
1,
J
J
ρ
ς
=
− (10.18)
or
000
1
,
m
J
Jj Jj
j
p
ρν
=
=
∑
(10.19)
with
0
J
j
r given by relation (10.5) which is perfectly coherent as relation (10.19)
represents the conditional mean of the non-risky interest rate given
0
J
.
3) no environment knowledge
In this last case, the investor just observes the initial value of the stock
0
S as in
the CRR or the Black and Scholes models. As above we can compute the
expectation of S(1) as follows:
()
(
)
(
)
000
(1) (1) ,
E
SS EESJS= (10.20)
and from relation (10.16):
(
)
(
)
0
00 0
(1) .
J
E
SS SE S
ς
= (10.21)
As, from relation (10.17), we get that:
()
0
0
11
.
mm
J
iijij
ij
E
Sapr
ς
==
=
∑∑
, (10.22)
it follows that the AOA is still true in this case with a non-risky interest rate
ρ
defined by:
11
1.
mm
iijij
ij
apr
ρ
==
=−
∑∑
(10.23)
From this last relation and relation (10.19), we get
i
111
11
1
(1 )
.
mmm
iij ij
iij
mm
iijij
ij
m
ii
i
aap
ap
a
ρ
ν
ν
ν
===
==
=
=− −
=
=
∑∑∑
∑∑
∑
(10.24)
206 Chapter 5
Once more, these last two relations show the perfect coherence concerning the
non-risky interest rates to be used with regard to the three environment
information sets that we can have.
10.1.2 Computational Option Pricing Formula For The One-Period Model
In the preceding section, relation (10.12) gives the value of a call option at time 0
given the initial and final environment states
01
,
J
J
. We now compute the price
of the option, firstly with only the knowledge at time 0 of the initial environment
state
0
J
, then with only the knowledge of the final state
1
J
and finally with no
knowledge of the initial and final states.
1) with the knowledge of
0
J
This value, denoted by
0
0
(,1)
J
CS , is nothing else than the conditional expectation
of
01
0
(,1)
JJ
CS given
0
J
:
(
)
001
0000
(,1) (,1) , ,
JJJ
CS EC S JS= (10.25)
or
000
00
1
(,1) (,1).
m
JJjJj
j
CS pC S
=
=
∑
(10.26)
2) with the knowledge of
1
J
Let
0
(,1)
j
CS represent the value of the call in this case when
1
J
j
=
; we have:
()
0010
1
( ,1) ( ,1)
m
j
ij
i
CS PJ iJ jCS
=
===
∑
. (10.27)
From the Bayes formula, we get:
()
(
)
()
01
01
1
1
,
iij
m
kkj
k
PJ iJ j
PJ iJ j
PJ j
ap
ap
=
=
=
===
=
=
∑
(10.28)
and so, from relation (10.27):
00
1
1
(,1) (,1).
m
iij
j
ij
m
i
kkj
k
ap
CS CS
ap
=
=
=
∑
∑
(10.29)
Let us note that this case is useful if the investor wants to anticipate the final
value of the environment state at time 0.

Black & Scholes extensions 207
3) with no knowledge of
0
J
and
1
J
In this case, with the help of relation (10.26), we can write that the call value
represented by
0
(,1)CS , is given by:
00
1
(,1) (,1),
m
ii
i
CS aC S
=
=
∑
(10.30)
or with the help of relation (10.29) with:
00
11
(,1) (,0).
mm
j
kkj
jk
CS apC S
==
=
∑∑
(10.31)
10.1.3 Examples
The application of our one-period model is already useful with only two or three
states. Indeed, it is quite natural to consider one state, for example state 0 to
model the normal economic and financial environment; then we can add a
supplementary state
− 1 to represent an abnormal situation like a crash or a
doped situation.
With three states, we can separate the crash possibility represented by state
− 1
from the doped situation represented by state 1, state 0 always being the normal
case.
Example 10.1: A two-states model
As said just above, let the state set be:
{
}
0,1I = (10.32)
with state 0 as the normal economic and financial situation environment and state
1 as the exceptional in the sense of, for example, a crash or doped situation.
Numerical data are the following:
(0.95,0.05),
0.98 0.02 1.03 1.05
,,
0.60 0.4 1.05 1.03
1.3 1.1 0.7 0.5
,.
1.06 1.2 0.4 0.6
=
⎡⎤⎡⎤
==
⎢⎥⎢⎥
⎣⎦⎣⎦
⎡⎤⎡⎤
==
⎢⎥⎢⎥
⎣⎦⎣⎦
a
Pr
UD
(10.33)
Example 10.2: A three-states model
Here, let the state set be:
{
}
1, 0,1 .I =− (10.34)
State 0 represents the normal economic and financial situation environment, state
−
1 the exceptionally bad situation in the sense of for example a crash situation
and state 1 as exceptionally good as a doped effect of the Stock Exchange for
example.
