Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability

218 Chapter 5

() ()1 () ()1

() ()1

() () () 1

() ()

'('),',,

(')

( ) (-),

Nt Nt Nt Nt J J

Nt Nt

J J J J Nt Nt Nt

Nt Nt

dS

dt dW t T t T T

St

ST ST

μσ

++

+

⎡

⎤

=+ −∈

⎣

⎦

=

(11.11)

where the process

() ()1

(('),'0)

JJ

Nt Nt

Wtt

+

≥

is a standard Brownian motion on

() ()1

,

Nt Nt

TT

+

⎡⎤

⎣⎦

defined on the basic probability space stochastically independent

of

()

() ()

,

Nt Nt

JX.

This model has the following financial meaning: at t=0, the asset starts from the

known initial value

0

S

, the known initial j-state

0

J

representing the state of the

initial economic and financial environment. On the time interval

1

X

, the asset

has the random volatility

1

σ

and has as stochastic dynamics the SDE (11.11)

with t=0; at time

1

X

, the J process has a transition to state

1

J

and on the time

interval

[

)

12

,TT , the asset has the random volatility

2

σ

and has as stochastic

dynamics the SDE (11.11) with N(t)=1 and so on....

We always define

0

0, . .

X

as=

So, it is now clear that we have in fact a perturbed Black and Scholes model due

to this random change of volatility; note that this model is quite general as, in

fact, we have a random volatility on each time interval

() ()1

,

Nt Nt

TT

+

⎡

⎤

⎣

⎦

.

Of course for m=1, we recover the classical Black-Scholes-Samuelson model for

the description of an asset.

11.2.2 The explicit expression of S(t)

Given

() () 1

,

Nt Nt

JJ

+

, the Itô calculus gives the solution of the SDE (11.11) :

2

() ()1

()

() ()1

'

2

(' )

()

() () 1

(') ,

',.

JJ

Nt Nt

JJ

Nt Nt

JJ Nt

Nt Nt

t

Wt T

Nt

Nt Nt

St S e e

tTT

σ

μ

σ

+

⎛⎞

⎜⎟

−

⎜⎟

−

⎝⎠

+

=

⎡⎤

∈

⎣⎦

(11.12)

Starting from the state

0

S at time 0 and given a scenario for the economic and

financial environment

01

( , ,..., ,...)

n

JJ J

, this expression gives the explicit form of

the trajectories of the process ( ( ), 0).St t≥

Now, given (

0 0 1 1 () () () 1 () 1

, , , ,..., , , ,

Nt Nt Nt Nt

JXJX J X J X

+

), from relation (11.12),

we get:

Black & Scholes extensions 219

()

() ()1

() ()1 () ()1

2

()

() () 1

(')

ln = ) ' ' ,

2

',,

JJ

Nt Nt

Nt Nt Nt Nt

JJ JJ Nt

Nt

Nt Nt

St

tWtT

S

tTT

σ

μσ

+

++

+

⎛⎞

⎜⎟

−+ −

⎜⎟

⎝⎠

⎡⎤

∈

⎣⎦

(11.13)

so that for

() () 1

',

Nt Nt

tTT

+

⎡⎤

∈

⎣⎦

:

() ()1

2

()

2

()

(')

ln ( ' ),

2

(' ),

JJ

Nt Nt

JJ Nt

Nt

JJ Nt

St

NtT

S

tT

σ

μ

σ

+

⎛⎞

⎜⎟

−−

⎜⎟

⎝⎠

−

≺

(11.14)

,()

() ()1

(' )

() 1

()

,,

JJ Nt

Nt Nt

tT

tNt

Nt

St

EJe

S

μ

+

−

+

⎛⎞

ℑ=

⎜⎟

⎝⎠

(11.15)

(

)

2

,() ()

() ()1 () ()1

2(') (')

() 1

()

var , 1

J J Nt J J Nt

Nt Nt Nt Nt

tT tT

tNt

Nt

St

Je e

S

μσ

++

−−

+

⎛⎞

ℑ= −

⎜⎟

⎝⎠

. (11.16)

Let us suppose that the random variables

00 11 () ()1 ()1

, , , ,..., , ,

Nt Nt Nt

SJXJ J X J

++

are

given; it follows that the conditional distribution function of

0

()St

S

is a log-normal

distribution, i.e.:

()

01 () ()1 () ()1

01

0

22

1()1()

()

ln

(), ().

Nt Nt JJ Nt Nt

JJ JJ Nt JJ Nt

St

S

NX tT X tT

μμ σσ

++

++ − ++ −

≺



(11.17)

11.3 Call Option Pricing

Now to get a useful model, let us proceed as in Janssen and Manca (1999); for a

fixed

t, we assume that all the parameters ,

μ

σ

only depend on

0()()1

,,

Nt Nt

JJ J

+

and

t is represented by

0()()1 0()()1

,

Nt Nt Nt Nt

JJ J JJ J

μ

σ

+

(11.18)

so that from relation (11.17):

0()()1 0()()1 0()()1

22

0

() 1

ln , .

2

Nt Nt Nt Nt Nt Nt

JJ J JJ J JJ J

St

N

tt

S

μσσ

+++

⎛⎞

−

⎜⎟

⎝⎠

≺ (11.19)

Of course, we can always simplify our basic assumption by suppressing the

dependence with respect to

() 1Nt

J

+

and even to

()Nt

J

.

220 Chapter 5

Nevertheless, we think that the dependence from the future environment state

() 1Nt

J

+

is quite important as it gives the possibility for the first time to model the

stochastic asset evolution taking into account this anticipation of the next future

state.

Let us now consider a European call option with

t as maturity time, K as exercise

price that we must price at time 0.

If we want to assume that there is no arbitrage possibility, we must impose that

0()()1 0()()1Nt Nt Nt Nt

JJ J JJ J

μ

δ

+

=

(11.20)

where

0()()1Nt Nt

JJ J

δ

+

represents the equivalent instantaneous non-risky return on

[0

,t] given

0()()1

,,

Nt Nt

JJ J

+

. Doing so, we will use the risk neutral measure under

which the forward value of the asset is a martingale; otherwise we work with the

initial “physical” measure more appropriate for insurance than for finance.

Knowing

0()()1

,,

Nt Nt

JJ J

+

and working with the risk neutral measure, we can

compute the value of the call at time 0 using the classical Black and Scholes

formula:

0()()1 0()()1 0()()1 0()()1

0()()1

0()()1 0()()1

0()()1

0()()1 0()()1 0

00 ,1 ,2

0

1

,1

,2 ,1

(,) ( ) ( ),

ln

1

,

2

Nt Nt Nt Nt Nt Nt Nt Nt

Nt Nt

Nt Nt Nt Nt

Nt Nt

Nt Nt Nt Nt

t

JJ J JJ J JJ J JJ J

JJ J

JJ J JJ J

JJ J

JJ J JJ J JJ

CStSd Kr d

S

Kr

dt

t

dd

σ

++++

+

++

+

++

−

=Φ − Φ

=+

=−

() ()1

0()()1

,

.

Nt Nt

JJ J

Nt Nt

J

JJ J

t

e

δ

ν

+

=

(11.21)

To get the formula of the call only knowing

00

,SJ, we must use the following

formula:

(

)

00()()1

000

() ( ,) , .

Nt Nt

JJJJ

Ct EC StJS

+

= (11.22)

From the theory of semi-Markov processes, we get:

(

)

0 0 () ()1

000

0

() ( ,) , ,

() () ( ,).

Nt Nt

JJJJ

JJjjkJjk

jIkI

Ct EC StJS

Ct PtpC St

+

∈∈

=

∑∑

(11.23)

If we have no information about the initial state

0

J

, we get of course the

following formula:

(

)

(

)

(

)

0 0 () ()1

000

() () ( ,) , ,

() ().

Nt Nt

JJJJ

ii

iI

Ct EC t EEC S t J S

Ct aC t

+

∈

==

=

∑

(11.24)

Remark 11.1 Numerical treatments are possible

Black & Scholes extensions 221

11.4 Stationary Option Pricing Formula

In option pricing, it is nonsense to let t tend towards

+

∞ ; nevertheless, we can

use the limit reasoning proposed by Janssen by supposing that on the time

horizon [0,t], the semi-Markov environment has more and more transitions in this

finite time period.

We can model this situation under the assumption that the conditional sojourn

time means , ,

ij

bij I∈ satisfy the conditions

()

,

1

0,

,

ij ij

ij n n n

b

bEXJ iJ j

ες ε

−

=>

=

==

(11.25)

so that:

,,

.

iijij ijiji

jI jI

iijij

jI

p

bp iI

p

ηεςεθ

θς

∈∈

∈

== =∈

=

∑∑

∑

(11.26)

From the asymptotic theory of semi-Markov processes, we know that:

()

() () 1

0

1

lim , , , ,

ijkjk

Nt Nt

m

ll

l

p

PJ jJ k ij I

ε

π

ς

πθ

+

→

=

== ∈

∑

(11.27)

where the vector

()

1

,...,

m

π

is the unique stationary distribution of the embedded

Markov chain of matrix

P supposed to be ergodic.

The new parameters , , ,

jk

ijk I

ς

∈

represent factors expressing the

proportionality of the sojourn in each environment state.

Now the result (11.23) becomes:

00

0

1

() ( ,).

jjkjk

JJjk

m

jI

ll

l

p

Ct C St

kI

π

ς

πθ

∈

=

∈

∑∑

∑

(11.28)

From (11.24), we get

0

1

() ( ,).

jjkjk

iijk

m

iI jI

ll

l

p

Ct a C S t

kI

π

ς

πθ

∈∈

=

∈

∑∑∑

∑

(11.29)

This last formula replaces the Black and Scholes formula without any a priori

information at time 0 except of course the initial value of the asset

0

S

.

In conclusion, the new model proposed here extends the classical Black and

Scholes formula in the case of the existence of an economic and financial

environment modelled with a homogeneous semi-Markov process taking into

222 Chapter 5

account this environment not only at the time of pricing but also before and after

the maturity date.

This new family of Black and Scholes formulae seems to be more adapted to the

reality, particularly when taking into account the anticipations of the investor or

the consideration of stress scenario in the philosophy of the VaR approach.

12 MARKOV AND SEMI-MARKOV OPTION PRICING

MODELS WITH ARBITRAGE POSSIBILITY

The aim of this last part is the presentation of new models for option pricing,

discrete in time and within the framework of Markov and semi-Markov processes

as an alternative to the classical Cox-Rubinstein model and giving arbitrage

possibilities. They were introduced by Janssen, Manca and Di Biase (1998). Both

cases of European and American options are considered and possible extensions

are given.

12.1 Introduction to the Janssen-Manca-Di Biase models

Let us consider an asset observed on a discrete time scale

{

}

0,1,..., ,... ,tTT

<

∞ (12.1)

having S(t) as market value at time t. To model the basic stochastic process

(S(t), t=0,1,...,T), (12.2)

we suppose that the asset has known minimal and maximal values so that the set

of all possible values is the closed interval

min max

[, ]SS partitioned in a subset of m

subclasses.

For example, if S

0

is the value of the asset at time 0, we can put:

max min

0

max min

,

2

, 1,..., ,

,

2

k

SS

S

SSkk

SS

υ

−

=

=+Δ=

=−Δ=

−

Δ=

(12.3)

υ

being arbitrarily chosen.

This implies that the total number of states is 2 1

υ

+

.In the sequel, we will order

these states in the natural increasing order and use the following notation for the

state space:

{ , ( 1),...,0,1,..., }.I

υ

υυ

=− − − (12.4)

We can also introduce different step lengths following up or down movements

and so consider respectively

,'.ΔΔ

It is also possible to let

Black & Scholes extensions 223

max

S →+∞ (12.5)

and

T →+∞ (12.6)

particularly to get good approximation results.

Let us suppose we want to study a call option of maturity T and exercise price

K=

0

k Δ

both in European and American cases bought at time 0.

So, in the European case, the intrinsic value of the option is given by:

() max{0,() }.CT ST K

=

− (12.7)

For the American case, the optimal time for exercising is given by the random

time

τ

such that:

1,...,

max max{0, } max{0, ).

t

tT

SK S K

τ

=

−

=− (12.8)

To get results, we must now introduce in the following section a stochastic model

for the S-process.

12.2 The Homogeneous Markov JMD (Janssen-Manca-Di

Biase) Model For The Underlying Asset

Let us suppose that we are working on the filtered probability space

(,,( ))

t

PΩℑ ℑ .

In our first model, we will suppose that the underlying asset S is a homogeneous

Markov chain with matrix:

ij

p

⎡

⎤

=

⎣

⎦

P (12.9)

on the state space I given by relation (12.4).

It follows that, at time t, given the knowledge of the asset value ( )

t

St S= the

market value of the option at time t, C(t), thus with a remaining maturity T-t and

exercise price K given by

0

,Kk

=

Δ has as probability distribution:

0

()

0,0

()

,

(() ( )) , ,

(() 0) .

Tt

Sj

Tt

Sj

lk

PCT j k p j k

PCT p

−

≤

=− Δ= >

==

∑

(12.10)

This result gives the possibility to compute all interesting parameters concerning

C. For example, the mean of C(t) has the value:

0

()

,0

(() () ) ( ).

Tt

tSj

lk

ECT St S p l k

−

>

=

=−Δ

∑

(12.11)

Of course, we have to compute the present value at time t with the non-risky unit

period interest rate r so that the value of the call at time t is given by:

224 Chapter 5

0

()

,0

() ( ( ) () ) ( ) ,

1

.

1

Tt Tt Tt

tSj

lk

Ct v ECT St S v p l k

v

r

−−−

>

===−Δ

=

+

∑

(12.12)

If the matrix

P is ergodic, then if Tt

−

is large enough, results (12.10) and

(12.11) can be well approximated by:

0

00

0

(() ( )) , ,

(() 0) , ,

(() () ) ( ),

() ( ) .

j

l

lk

tj

lk

Tt

j

lk

PCT j k j k

PCT j k

ECT St S l k

Ct v l k

π

≤

>

−

>

=− Δ= >

== ≤

=

=−Δ

∑

(12.13)

Of course the vector

0

( ,..., ,..., )

ν

π

πππ

−

=

(12.14)

is the steady-state vector related to the matrix

P.

12.3 Particular Cases

As we said in our introduction, our homogeneous Markov model contains as a

very special case the famous CRR binomial model but with fixed minimal and

maximal values. It suffices to select a Markov matrix

P with the structure

**00 0000

*0*0 0000

0*0* 0000

00*0 0000

0000 0*00

0000 *0*0

0000 0*0*

0000 00**

⎡⎤

⎢⎥

⎣⎦







(12.15)

and as the Cox-Rubinstein model has a multiplicative form, we can consider that:

00

(1),1, ,

(1 ) , 1, .

uSuSS

dS d S S

−>>

⎧

Δ=

⎨

−<<

⎩

(12.16)

Black & Scholes extensions 225

Remark 12.1 Under (12.5), the matrix P has an infinite number of rows and

columns.

We can also get the

trinomial model if we put in (12.15) a non-zero main

diagonal and so on.

12.4 Numerical Example For The JMD Markov Model

To illustrate numerically our first model, let us suppose that we are interested in

an asset whose possible values are restricted to the following ones;

maximum value: state 3=1650,

intermediary values: state 2=1600, state 1=1550, state 0=1500,

state

− 1=1450, state − 2=1400,

minimum value: state

− 3=1350.

With the used notation, this means that

0

1500, 50.S

=

Δ= Moreover, we also

suppose that the transition matrix

P, with as unit step the week, is given by

1111

000

6336

11111

00

36666

121111

0

777777

111

00 00

244

2311

00 0

7777

12211

00

77777

1111

000

2488

⎡⎤

⎢⎥

⎣⎦

. (12.17)

It is easily seen that the matrix P is ergodic with as unique stationary distribution:

(0.10002, 0.13336, 0.27228, 0.23737, 0.16927, 0.07539, 0.01231).

Then starting at time 0 in state 1500 with a maturity time of 16 weeks, the

asymptotic value of the European call option expectation with 1500 as exercise

price is 41.95 and the call value at time 0 is 41.328.

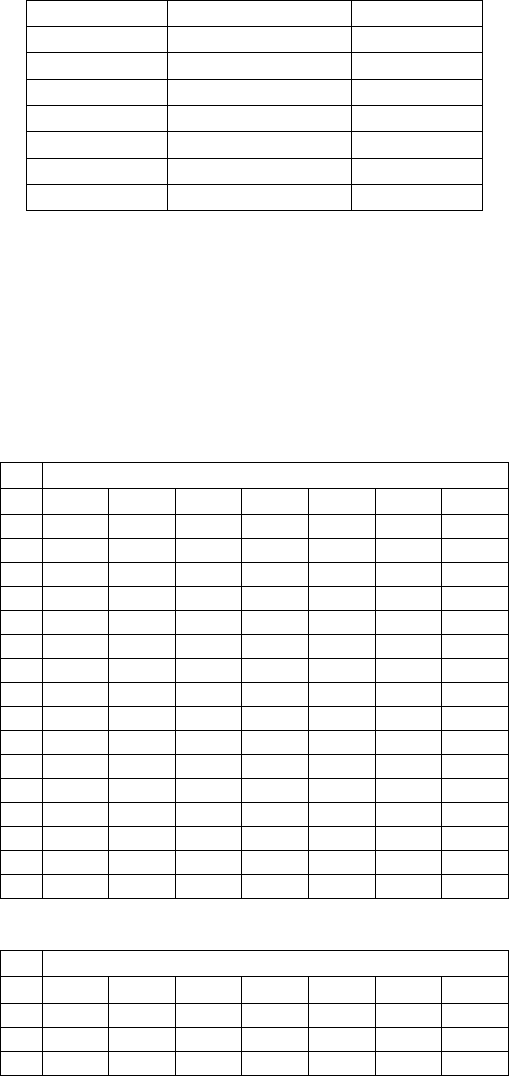
Table 12.1 gives option expectations and option values with different exercise

prices:

226 Chapter 5

Exercise price Option expectation Option value

1350 174.106 171.512

1400 124.721 122.826

1450 79.1059 77.927

1500 41.9538 41.328

1550 16.6704 16.422

1600 5.00113 4.927

1650 0 0

Table 12.1: Markov option computation

Let us now consider the transient behaviour, meaning that we will consider the

maturity as a parameter expressed in n weeks.

Table 12.2.1, gives option

expectations, Table

12.2.2 option values with as exercise price 1500 and for

different maturity times from 1 to 16 weeks.

STATE

n

-3 -2 -1 0 1 2 3

1 75.00 75.00 57.14 25.00 14.29 7.14 0.00

2 60.71 53.57 46.93 38.39 30.10 20.41 16.96

3 50.02 48.40 43.39 40.60 37.08 31.61 31.39

4 45.70 44.92 42.79 41.11 39.61 37.39 37.44

5 43.70 43.30 42.35 41.57 40.84 39.87 39.81

6 42.76 42.58 42.13 41.78 41.45 40.98 40.96

7 42.33 42.24 42.04 41.87 41.72 41.50 41.50

8 42.13 42.09 41.99 41.92 41.84 41.75 41.74

9 42.03 42.02 41.97 41.94 41.90 41.86 41.86

10 41.99 41.98 41.96 41.95 41.93 41.91 41.91

11 41.97 41.97 41.96 41.95 41.94 41.93 41.93

12 41.96 41.96 41.96 41.95 41.95 41.94 41.94

13 41.96 41.96 41.95 41.95 41.95 41.95 41.95

14 41.96 41.96 41.95 41.95 41.95 41.95 41.95

15 41.95 41.95 41.95 41.95 41.95 41.95 41.95

16 41.95 41.95 41.95 41.95 41.95 41.95 41.95

Table 12.2.1: option expectation

STATE

n

-3 -2 -1 0 1 2 3

1 70.93 74.93 57.09 24.98 14.27 7.14 0.00

2 60.60 53.47 46.85 38.32 30.05 20.37 16.93

3 49.88 48.27 43.26 40.48 36.98 31.53 31.31

Black & Scholes extensions 227

4 45.53 44.75 42.63 40.26 39.45 37.25 37.30

5 43.50 43.10 42.15 41.38 40.65 39.68 39.63

6 42.22 42.34 41.90 41.54 41.21 40.75 40.73

7 42.05 41.97 41.76 41.60 41.45 41.23 41.22

8 41.81 41.77 41.68 41.60 41.53 41.43 41.43

9 41.68 41.66 41.62 41.58 41.55 41.51 41.50

10 41.60 41.59 41.57 41.55 41.54 41.52 41.52

11 41.54 41.54 41.53 41.52 41.51 41.50 41.50

12 41.49 41.49 41.49 41.48 41.48 41.47 41.47

13 41.45 41.45 41.45 41.44 41.44 41.44 41.44

14 41.41 41.41 41.41 41.41 41.41 41.41 41.40

15 41.37 41.37 41.37 41.37 41.37 41.37 41.37

16 41.33 41.33 41.33 41.33 41.33 41.33 41.33

Table 12.2.2: option value

12.5 The Continuous Time Homogeneous Semi-Markov

JMD Model For The Underlying Asset

With the generalisation of electronic trading systems, it seems more adapted to

construct a time continuous model for which the changes in the values of the

underlying process may depend on the time it remained unchanged before a

transition.

Also, let

(( , ) 0,1,...)

nn

ST n

=

(12.18)

be the successive states and time changes of the considered asset.

The Janssen-Manca semi-Markov continuous model without AOA starts from the

basic assumption that the process (12.18) is a semi-Markov process of kernel

Q.

It follows that, at time t in state S(t)=S

t

, the market value of the considered

European option with maturity Tt

−

has as probability distribution at maturity

time

0

00

0

(() ( )) ( ), ,

(() 0) ( ), .

t

Sj

lK

PCT j k T t j k

PCT T t j k

φ

≤

=− = − >

== − ≤

∑

(12.19)

Of course, the matrix ( )t

Φ represents the transition probabilities for the

considered semi-Markov process (see Chapter 3, relation (10.2))

This result gives the possibility to compute all interesting parameters concerning

C. For example, the mean of C(T) has the value:

0

(() () ) ( )( ).

t

tSj

jk

ECT St S T t j k

φ

>

=== −−Δ

∑

(12.20)

The pricing of the option at time t is here given by the conditional market value

C(t):

Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability

Подождите немного. Документ загружается.