Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability
Подождите немного. Документ загружается.

Discrete time SMP and numerical solution 167
()
11
1
(,) 1 (, )( ) (,)( )
(,) (,).
km
ii iili
ul
km
il l
ul
Vuk Huk k u b u u
bu V k
τ
τ
ψ
ττ ψ
ττ
=+ =
==
≅− − + −
+
∑∑
∑∑
(8.8)
As we know that
(0) 0
ij
b =
and
(,) 0
ij
buu
=
, i,j=1,…,m, relations(8.7) and (8.8)
correspond in fact to the evolution equations (5.5) and (5.6).
As for the second case, we will now give the numerical solution of the evolution
equations of (5.13) and (5.17), respectively for homogeneous and non-
homogeneous cases.
Let us recall these two equations:
()
111
11 1 11
() 1 () () ( )( )
() () ()( ),
kkm
iii ilil
l
km km
il i il l
ll
Vkh Hkh h h h Q h h
hQhhhhQhVkhh
τϑ
ϑ
ϑτϑ
ψτ ϑ γ ϑ
ϑ
ψτ ϑ ϑ
===
== = ==
=− +
⎛⎞
++−
⎜⎟
⎝⎠
∑∑∑
∑∑ ∑ ∑∑
(8.9)
()
1
11 1
11
(,) 1 (,) (,)
(, ) (,)
(, )(,) (, )(, ).
k
iiil
u
km
il i
ul u
km km
il l il il
ul ul
Vuhkh Huhkh h uh h
h Q uh h h uh h
h Q uh h V h kh h Q uh h uh h
τ
ϑ
ϑτ
ϑϑ
ψτ
ϑψτ
ϑ
ϑϑγϑ
=+
=+ = =+
== ==
=−
⎛⎞
+
⎜⎟
⎝⎠
++
∑
∑∑ ∑
∑∑ ∑∑
(8.10)
Proceeding as for the first case, we obtain:
()
1111
11 11
() 1 () () () ()
() () () ( ),
kkm
iii ili
l
km km
il il il l
ll
Vk Hk b
bbVk
ϑ
τϑ τ
ϑϑ
ψ
τϑψτ
ϑγ ϑ ϑ ϑ
====
== ==
⎛⎞
=− +
⎜⎟
⎝⎠
++−
∑∑∑∑
∑∑ ∑∑
(8.11)
()
11
11 1 1
(,) 1 (,) (,) (, ) (, )
(, ) (,) (, ) (,),
kkm
iiiilil
uul
km km
il i il l
ul u ul
Vuk H uk u b u u
bu u bu V k
τϑ
ϑ
ϑτϑ
ψ
τϑγϑ
ϑψτ ϑϑ
=+ = =
=+ = =+ = =
=− +
⎛⎞
++
⎜⎟
⎝⎠
∑∑∑
∑∑ ∑ ∑∑
(8.12)
so that relations (8.11) and (8.12) correspond in fact to relations (5.10) and
(5.14).
168 Chapter 4
8.2 Discounted Case
The change from continuous and discrete time in discounted cases implies that
the financial discounting factors should change; in the case of constant intensity
interest rate
δ
, it results that
()
1
1
h
h
re
δ
−
−
+=, (8.13)
and in the case of variable intensities respectively for homogeneous and non-
homogeneous cases:
()
()
(1)
(1)
()
1
(,)
1
1() , 1,,,
1(,) , 1,,.
h
h
h
h
d
h
ud
h
re k
ru e u k
τ
τ
τ
τ
δθ θ
δθθ
ττ
ττ
−
−
−
−
−
−
∫
+= =
∫
+= =+
…
…
(8.14)
(for more details on this topic see Volpe di Prignano (1985), Kellison(1991).
Now we will present two cases in the discounted environment: the discretization
of relations (5.23), (5.24) and then of relations (5.29) and (5.33).
For the first case, the discretization method gives as relations:
()
()
11
11
() 1 () ( )
()( )1 ,
hh
km
iiiili
kr r
l
km
il l h
l
Vkh Hkh a h Q ha
hQhVkhhr
ϑ
ϑ
ϑ
ϑ
ψ
ϑψ
ϑϑ
==
−
==
=− +
+−+
∑∑
∑∑
(8.15)
()
()
11
()
11
(,) 1 (,) (, )
(, )( ,)1 .
hh
km
iiiili
kur ur
l
km
u
il l h
l
Vuhkh Huhkh a h Q uh ha
hQuhhVhkhr
ϑ
ϑ
ϑ
ϑ
ψ
ϑψ
ϑϑ
−−
==
−−
==
=− +
++
∑∑
∑∑
(8.16)
Proceeding in the same way we use to get relations (8.7) and (8.8), the following
results are obtained:
()
()
11
11
() 1 () ()
() ( )1 ,
km
iiiili
kr r
l
km
il l
l
Vk Hk a b a
bVk r
ϑ
ϑ
ϑ
ϑ
ψ
ϑψ
ϑϑ
==
−
==
=− +
+−+
∑∑
∑∑
(8.17)
()
()
11
()
11
(,) 1 (,) (, )
(, ) (, )1 ,
km
iiiili
kur ur
l
km
u
il l
l
Vuk Huk a b u a
bu V k r
ϑ
ϑ
ϑ
ϑ
ψ
ϑψ
ϑϑ
−−
==
−−
==
=− +
++
∑∑
∑∑
(8.18)
corresponding to relations (5.19) and (5.23).
For the second case, let us begin with the discretization of the equation (5.29)
leading to:
Discrete time SMP and numerical solution 169
() ()
()
()
()
1
11
1
11 1 1
1
11 1
1
11 1
() 1 () ( ) 1 ()
() () 1 ()
()() 1 ()
()( ) 1 ().
k
iiih
km
il i h
l
km
il il h
l
km
il l h
l
Vkh Hkh h h r
hQhh h r
hQhh r
hQhVkhh r
ϑ
ϑτ
ϑθ
ϑθτ
ϑ
ϑτ
ϑ
ϑτ
ψϑ τ
ϑψθ τ
ϑγϑ τ
ϑϑ τ
−
==
−
== = =
−
== =
−
== =
=− +
++
++
+−+
∑∏
∑∑ ∑ ∏
∑∑ ∏
∑∑ ∏
(8.19)
Once more, proceeding in the same way we use to find relations (8.7) and (8.8),
we get:
()
() ()
() ()
1
11 1 1
11
11 1 11 1
1
11
() () () 1 ()
() () 1 () () ( ) 1 ()
1() ()1(),
km
iili
l
km km
il il il l
ll
k
ii
Vk b r
brbVkr
Hk r
ϑθ
ϑθτ
ϑϑ
ϑτϑ τ
ϑ
ϑτ
ϑψθ τ
ϑγ ϑ τ ϑ ϑ τ
ψϑ τ
−
== = =
−
−
== = == =
−
==
=+
+++−+
+− +
∑∑ ∑ ∏
∑∑ ∏ ∑∑ ∏
∑∏
(8.20)
this result corresponding to relation (5.25).
Finally, we have to dicretize the equation (5.33):
()
() ()
()
1
11 1 1
1
11
1
11 1
1
(,) (, ) (, ) 1 (,)
1(,) (,)1(,)
(, )(, ) 1 (,)
(, )(,)
km
iilih
ul u
k
ii h
uu
km
il il h
ul u
m
il l
ul
Vuhkh h Q uh hh uh h ru
Huhkh h uh h ru
hQuhhuhh ru
hQuhhVhkh
ϑθ
ϑθτ
ϑ
ϑτ
ϑ
ϑτ
ϑ
ϑψθ τ
ψϑ τ
ϑγ ϑ τ
ϑϑ
−
=+ = =+ =
−
=+ =+
−
=+ = =+
=+ =
=+
+− +
++
+
∑∑ ∑ ∏
∑∏
∑∑ ∏
∑
()
1
11
1(,).
k
h
u
ru
ϑ
τ
τ
−
=+
+
∑∏
(8.21)
And as above, we get the result corresponding to relation (5.31)
()
() ()
()
()
1
11 1 1
1
11
1
11 1
1
11 1
(,) (, ) (, ) 1 (,)
1 (,) (, ) 1 (,)
(, ) (, ) 1 (,)
(, ) ( ,) 1 (,) .
km
iili
ul u
k
iil
uu
km
il il
ul u
km
il l
ul u
Vuk b u u ru
Huk u ru
bu u ru
bu V k ru
ϑθ
ϑθτ
ϑ
ϑτ
ϑ
ϑτ
ϑ
ϑτ
ϑψθ τ
ψϑ τ
ϑγ ϑ τ
ϑϑ τ
−
=+ = =+ =
−
=+ =+
−
=+ = =+
−
=+ = =+
=+
+− +
++
++
∑∑ ∑ ∏
∑∏
∑∑ ∏
∑∑ ∏
(8.22)
Chapter 5
SEMI-MARKOV EXTENSIONS OF THE BLACK-
SCHOLES MODEL
1 INTRODUCTION TO OPTION THEORY
During the last thirty years, financial innovation has generalised the systematic
use of new financial instruments such as options and swaps, mainly motivated for
hedging but also, sometimes, used as speculative tools.
So, let us begin by recalling the basic definition of option theory.
Definition 1.1 A call option (resp. put option) is a contract giving the right to
buy (resp. to sell) a financial asset, called an underlying asset, for a fixed price,
called exercise price, at the end of the contract time, called maturity time, also
laid down in the contract.
If one can exercise the option at any time before maturity, this type of option is
called of an American type; if one can exercise it only at maturity, the option is
called of a European type.
Let us use the following notation:
K: exercise price,
T: maturity time,
S: value of the underlying asset at maturity.
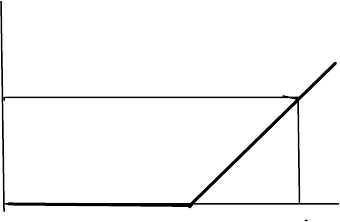
Then the “gain” of the holder of a European option at maturity time T is
represented by the following graph.
0
K
S
S-K
Figure 1.1: call option: holder’s gain at maturity
172 Chapter 5
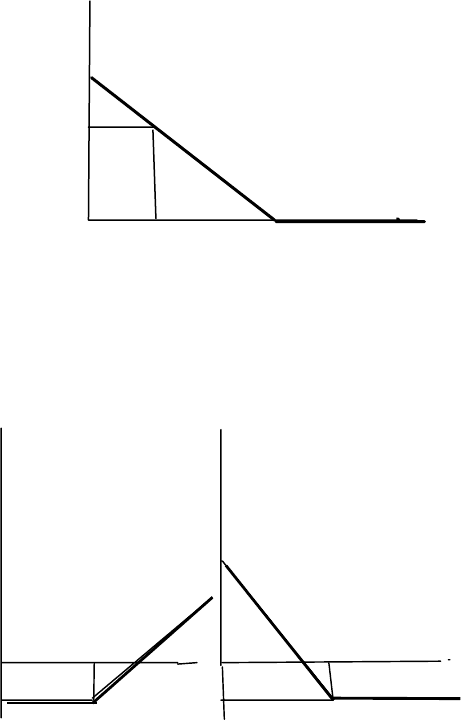
For the holder of a put, this graph becomes:
K
K
S
K-S
Figure 1.2: put option: holder’s gain at maturity
Of course, to get the “net gain”, we must estimate the cost of the option, often
called option premium, and furthermore transaction costs and taxes.
Let us represent respectively by C and P the premiums of call and put options.
So, we get, without taking into account transaction costs and taxes, the following
two graphical representations
-C
-P
K
K+C K-P
K
CALL PUT
Figure 1.3: call and put options: net gains at maturity for the holder
The main problem is called the pricing of optional products, that is to give within
the framework of an economic-financial theory framework, the values of
premiums C and P as a function of the maturity T and the value of the asset at
time 0.
More generally, as the holder of an option can sell his option on the option
market at any time t, 0<t<T, it is also necessary to give the “fair” value of the
option at this time t knowing that the underlying asset has, at this time, the value
S=S(t).
Black & Scholes extensions 173
Commonly, this fair market value is represented by
),(
τ
SC
(1.1)
where
tT
−
=
τ
(1.2)
represents the maturity computed at time t.
Sometimes, it is also useful to represent the call value as a function of the time
C(S,t).
We see here that it is absolutely necessary to make assumptions about the
stochastic process
(
)
.0),( TttSS
≤
≤
=
(1.3)
Concerning the economic-financial theory framework, we adopt the assumption
of efficient market, meaning that all the information available at time t is
reflected in the values of the assets and so, transactions having an abnormally
high profitability are not possible.
More precisely, an efficient market satisfies the following assumptions:
1. absence of transaction costs,
2. possibility of short sales,
3. availability of all information to all the economic agents,
4. perfect divisibility of assets,
6. continuous time financial market.
Furthermore, the market is complete; meaning that there exist zero-coupon
bonds without risk for all possible maturities.
Let us remark that the word “information” used in point 3 can have different
interpretations: weak, semi-strong or strong depending on if it is based on past
prices, or on all public information or finally on all possible information that the
agent can find.
According to Fama (1965), the efficient assumption justifies the “random walk”
model in discrete time, saying that if
()
i
R
s
Δ
represents the increment of an asset i
between s and s+1, we have:
() ()
iii
R
ss
μ
ε
Δ
=+
, (1.4)
i
μ
being a constant and ( ( ))
i
s
ε
a sequence of uncorrelated r.v. of mean 0,
sometimes called errors.
If we add the assumptions of equality of variances and of normality of the
sequence
(())
i
s
ε
, we get in fact a special case of the classical random walk
introduced in Chapter 3.
If the efficiency assumption seems to be natural, some empirical studies show
that it is not always the case in particular, since some agents can have access to
preference information in principle forbidden by the legal authority.
Nevertheless, should such agents use the pertinent information it will be quickly
noticeable by those markets and balance between agents will be restored.
This possibility, also called the case of asymmetric information, was studied by
174 Chapter 5
Spence, Akerlof and Stiglitz, who was awarded the Nobel Prize in Economics in
2001.
From a personal point of view, the authors think that if the efficiency assumption
seems quite normal for the long term, i.e., with a time unit large enough,
however, it does not always seem to be true locally, i.e., with a short time unit.
Indeed deregulation of markets where investors are willing to accept very small
benefits in a short time but with many transactions plainly explains the intense
activity of, for example, the currency markets which get very small benefits.
Due to the possibility of arbitrage, this is virtually making money without any
investment otherwise known as “free lunch”.
That is why models for asymmetric information should always be short term
models rejecting the AOA assumption.
To be complete, let us remark that it is now possible to construct models without
the AOA assumption but with assumptions on the time asset evolution and a
selection of different possible scenarios, so that the investor can predict what will
happen if such scenarios occur (cf Janssen, Manca et Di Biase (1997) and
Jousseaume (1995)).
To conclude this section, let us emphasize the fact that traditional option pricing
needs the efficiency of market dynamics and so of the AOA and also the choice
of a stochastic model for the underlying asset time evolution.
Therefore we will begin this chapter with a presentation of the two most used
classical models: the
Cox-Ross-Rubinstein model in discrete time and the
Black-Scholes model in continuous time. Then we will give the semi-Markov
extension of these two models presented by Janssen and Manca (1999) and
finally a non semi-Markov model with possibility of arbitrage (Janssen, Manca et
Di Biase (1997)).
2 THE COX-ROSS-RUBINSTEIN (CRR) OR BINOMIAL
MODEL
The model we will present here has the advantage of being quite simple in a
financial world not always open to the use of sophisticated mathematical tools
such as those used by Black and Scholes in 1973 to get their famous formula.
And so the CRR model, though coming later, was very good for the use of the BS
formula since, in the limit, the CRR model gives this formula again.
Moreover, the CRR model has still its own utility for financial institutions using
discrete time models even with a short time period.
Black & Scholes extensions 175
2.1 One-Period Model
To begin with, let us consider a model with only one time period, from time 0 to
time 1; the time unit can be chosen as the user wishes: a quarter, a month, a
week, a day, an hour,….
The basic assumption concerning the stochastic evolution of the underlying asset
is that, starting from value
0
(0)SS
=
at time 0, it can only get two values at the
end of the time period:
0
(1)uS u > if there is an up movement or
0
(0 1)dS d<<
in the case of a down movement, parameter u and d being supposed to be known
for the moment.
The probability measure is thus defined by the probability q of an up movement
and to avoid trivialities, we will assume that:
01.q
<
< (2.1)
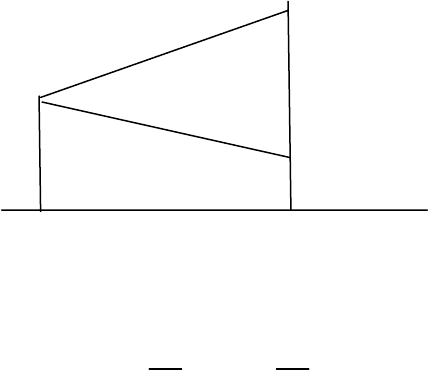
The next figure shows the two possible trajectories with of course
1.
p
q
=
− (2.2)
0
1
S(0)
S(1)=uS(0)
S(1)=dS(0)
u
d
q
p
Figure 2.1: one-period binomial model
If one prefers to work with the percentages x and y respectively of gain and loss,
we can express u and d as follows:
1,1.
100 100
x
y
ud
⎛⎞⎛⎞
=+ =−
⎜⎟⎜⎟
⎝⎠⎝⎠
(2.3)
We also suppose that there is no dividend distribution during the period.
Let us now consider an investor wishing to buy a European call on time 0 with
maturity 1 and with K as exercise price.
The
problem is thus to fix the premium of this call, that which the investor has to
pay at time 0 to buy this call, knowing the value S
0
of the underlying asset at time
0.
176 Chapter 5
2.1.1 The Arbitrage Model
If the investor wants to buy a call, it is clear that he anticipates an up movement
of the call so that exercising the call at the end of the period will be advantageous
for him and of course for the seller of the call the reverse will happen.
Nevertheless, the investor would take as little risk as possible knowing that he
has always the possibility to invest on the non-risky market giving a fixed
interest rate i per period.
To build a theory taking into account the apparently contradictory points of view,
modern financial theory is based on the principle of absence of arbitrage
opportunity (in short the AOA principle) meaning that there is no possibility to
gain money without any investment, that is, there is no possibility of getting a
free lunch.
This principle implies that the parameters d, u and i of the model must satisfy the
following inequalities:
1diu
<
+<
.
(2.4)
Indeed, let us suppose for example that the first inequality is not true. In this case
the investment in the asset is always better than the investment in the non-risky
market. Then if we borrow the sum
0
S from the bank and buy the asset, at the
end of the period we gain for sure the amount
(
)
0
(1 ) ,diS−+ and this is a free
lunch.
Similarly, if the right-hand inequality is false, we can sell the asset at time 0 to
get it to the seller at time 1 and so, the minimum value of the free lunch is in this
case
0
(1 )iuS+− , so that in both cases
,
the AOA principle is not satisfied.
As the seller of a call option, for example, has the obligation to sell the shares if
the holder of the call exercises his right, he must be able to do it whatever the
value of the considered share is; that is why we have to introduce the important
concept of hedging.
To do so, let us consider a portfolio in which at time 0 we have
Δ
shares and an
amount B of money invested at the non-risky rate i per period.
B may be negative in case of a loan given by the bank.
Under the AOA assumption, the investment in the call must follow the same
random evolution as the considered portfolio so that we have the following
relations for t=1:
00
00
(1) (1 ) ,
(1) (1 ) ,
u
d
CuS iB
CdS iB
=
++
=++
(2.5)
where
0
0
(1) max{0, },
(1) max{0, }.
u
d
CuSK
CdSK
=
−
=−
(2.6)
The system (2.5) is a linear system with two unknown values
,.
B
Δ
The unique solution is given by:

Black & Scholes extensions 177
0
(1) (1)
,
()
(1) (1)
.
()(1)
ud
du
CC
udS
uC dC
B
ud i
−
Δ=
−
−
=
−+
(2.7)
Now, as said above, from the AOA assumption, the value of the call at 0t = ,
denoted for the moment by
(
)
0
,0CS , is equal to the initial value of the portfolio
so that:
000
00
0
(,1) ,
(1) (1) (1) (1)
(,1) .
() ()(1)
ud d u
CS S B
C C uC dC
CS S
udS ud i
=Δ+
−−
=+
−−+
(2.8)
We can also write this value in the following form:
[]
0
1
( , 0) (1) (1 ) (1) ,
1
1
.
ud
CS qC qC
i
id
q
ud
=+−
+
+−
=
−
(2.9)
This last expression shows that the value of the call at the beginning of the period
can be seen as the present value of the expected value of the “gain” at the end of
the period. But this expectation is computed under a new probability measure
defined by
q , called risk neutral measure in opposition to the initial measure
defined by q, and called the historical or physical measure.
From assumption (2.4), this risk neutral measure is unique and moreover
independent of q, that is on the historical measure.
This shows that whatever the investor anticipates about the price of the
considered underlying asset, using this model, he will always get the same result
as another investor.
However, it must be clear that this risk neutral measure only gives an easy way to
compute the “fair” value of the call, but if we want to compute probabilities of
events, such as for example the probability of exercising the call at the end of the
period, then it is the historical measure that must be used.
2.1.2 Numerical Example
Let us consider the data
0
80, 80, 1.5, 0.5, 3%.SKudi===== (2.10)
It follows from the following model:
{
}
{}
(1) max 0.80 1.5 80 40,
(1) max 0.80 0.5 80 0.
u
d
C
C
=×−=
=×−=
(2.11)
The value of
q is obtained, i.e.,
