Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability
Подождите немного. Документ загружается.


Discrete time SMP and numerical solution 137
1
11
() exp , 1, ,
11
N
N
k
NN
mw c kh
hkN
mhwc mhwc
τ
η
⎛⎞
≤=
⎜⎟
−−
⎝⎠
…
. (2.30)
Remark 2.2 In the non-homogeneous case, as s is fixed in the system of integral
equations (2.2),
τ
is the only parameter, so for each
[
]
0,
s
Y∈ the result of
Theorem 2.1 holds.
3. DTSMP AND SMP NUMERICAL SOLUTIONS
In the previous section, we gave general formulas for the discretization of
continuous time HSMP and NHSMP with a finite number of states. With the
most simple quadrature method (rectangle formula), we get:
11
() () ( ) (),
mk
ij ij lj il
l
kh d kh h kh h Q h
τ
φφττ
==
⎛⎞
=+ −
⎜⎟
⎝⎠
∑∑
(3.1)
11
(,) (,) (,) (,).
mk
ij ij lj il
lu
uhkh d uhkh h hkhQ uh h
τ
φφττ
==+
⎛⎞
=+
⎜⎟
⎝⎠
∑∑
(3.2)
Here, the sum on the time starts from 1 (u+1) as, the probability of changing state
with a waiting time 0 is 0. Substituting in relations (3.1) and (3.2) the differential
with the increment and with h=1, it results that:
()
11
() () ( ) () ( 1) ,
mk
ij ij lj il il
l
kdk k Q Q
τ
φφτττ
==
⎛⎞
≅+ − −−
⎜⎟
⎝⎠
∑∑
(3.3)
()
11
(,) (,) (, ) (,) (, 1) .
mk
ij ij lj il il
lu
uk duk k Qu Qu
τ
φφτττ
==+
⎛⎞
≅+ −−
⎜⎟
⎝⎠
∑∑
(3.4)
Furthermore, taking into account relations (1.9) and (1.10) it results that
11
() () ( ) ()
mk
ij ij lj il
l
kdk k b
τ
φ
φττ
==
≅+ −
∑∑
, (3.5)
11
(,) (,) (,) (,).
mk
ij ij lj il
lu
uk d uk kb u
τ
φ
φτ τ
==+
≅+
∑∑
(3.6)
In this way, the evolution equations of the (DTHSMP) and (DTNHSMP) as
defined in relations (1.19) and (1.20) are obtained:
11
() () ( ) (),
mk
ij ij lj il
l
kdk k b
τ
φ
φττ
==
=+ −
∑∑
(3.7)
11
(,) (, ) (,) (,).
mk
ij ij lj il
lu
uk d uk kb u
τ
φ
φτ τ
==+
=+
∑∑
(3.8)
If the discretization step is h, then relations (3.7) and (3.8) become:
11
() () () (( ))
mk
hh hh
ij ij il lj
l
kh d kh b h k h
τ
φτφτ
==
=+ −
∑∑
, (3.9)
138 Chapter 4
11
(,) (,) (,) (,).
mk
hh hh
ij ij il lj
lu
uh kh d uh kh b uh h h kh
τ
φτφτ
==+
=+
∑∑
(3.10)
Now the equations (3.9) and (3.10) can be rewritten in matrix form as follows:
1
() () () (( )),
k
hh hh
kh kh h k h
τ
ττ
=
=+ ∗−
∑
Φ DBΦ (3.11)
1
(,) (,) (,) (,),
k
hh hh
u
uh kh uh kh uh h h kh
τ
ττ
=+
=+ ∗
∑
Φ DBΦ (3.12)
or equivalently:
1
() () (( )) (),
k
hhh h
kh h k h kh
τ
ττ
=
−∗−=
∑
Φ B Φ D (3.13)
1
(,) (,) (,) (,), , .
k
hhhh
u
uh kh h kh h kh uh kh k u k
τ
ττ
=+
−∗=∈≤
∑
Φ B Φ D (3.14)
Taking into account that k ∈
, both equations (3.13) and (3.14) can be written
more compactly as:
.
hh h
∗=U Φ D (3.15)
For the homogeneous case, it results that:
()
(2 ) ( )
(3 ) (2 ) ( )
h
h
hh
hhh
h
hh
hhh
⎡⎤
⎢⎥
−
⎢⎥
=
−−
⎢⎥
⎢⎥
−−−
⎢⎥
⎢⎥
⎣⎦
I000
BI00
U
BB I0
BBBI
, (3.16)
(0)
()
(2 )
(3 )
h
h
h
h
h
h
h
h
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
Φ
Φ
Φ
Φ
Φ
,
(0)
()
(2 )
(3 )
h
h
h
h
h
h
h
h
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
D
D
D
D
D
and in the non-homogeneous case:
(0, ) (0,2 ) (0,3 )
(,2) (,3)
(2 ,3 )
hh h
hh
h
h
hh h
hh hh
hh
−− −
⎡⎤
⎢⎥
−−
⎢⎥
⎢⎥
=
−
⎢⎥
⎢⎥
⎢⎥
⎣⎦
IB B B
0I B B
U
00 I B
00 0 I
, (3.17)
Discrete time SMP and numerical solution 139
(0, ) (0,2 ) (0,3 )
(,2) (,3)
.
(2 ,3 )
hh h
hh
h
h
hh h
hh hh
hh
⎡⎤
⎢⎥
⎢⎥
⎢⎥
=
⎢⎥
⎢⎥
⎢⎥
⎣⎦
ID D D
0ID D
D
00 I D
00 0 I
The following theorem holds for both homogeneous and non-homogeneous
cases.
Theorem 3.1 Equations (3.13) and (3.14) admit a unique solution.
Proof The determinant of matrix
h
U is absolutely convergent (Riesz (1913));
more precisely
det( ) 1
h
=U and consequently matrix
h
U is invertible.
In the homogenous case equation (3.13) can be seen as an infinite linear system
with an infinite number of unknowns. It ensues from Theorem 3.1 that the
system is solvable.
To solve such a system it is usually necessary to apply the truncation method
Riesz (1913); but in our case, it is very simple to find the solution.
Obviously, (0)
h
=Φ I and, once (0)
h
Φ is known we get:
() () (0) ()
hhhh
hh h=∗+Φ B Φ D
. (3.18)
Once (0), ( ), , ( )
hh h
hkhΦΦ Φ… are known, then:
1
1
(( 1) ) ( ) (( 1 ) ) (( 1) )
k
hhh h
kh h k h kh
τ
ττ
+
=
+= ∗ +−+ +
∑
Φ B Φ D (3.19)
and it is not necessary to apply the truncation method. Furthermore, these results
are obtained without any matrix inversion.
As in the homogeneous case, equation (3.14) can be seen as an infinite linear
system with an infinite number of unknowns, but the non-homogeneous matrix
equation is different from the homogeneous one because the coefficient matrix is
upper triangular in the non-homogeneous case and lower triangular in the
homogeneous.
Also in this case the truncation method should not be applied. In the
homogeneous case this result is trivial. In the non-homogeneous case the result is
not so immediate. We report, with more precision, the following result given in
and Janssen and Manca (2001a).
Proposition 3.1 The solution of the infinite order linear system (3.14) can be
given explicitly step by step.
Proof For the proof see Janssen-Manca (2001a)
140 Chapter 4
Remark 3.1 Here it should also be mentioned that the upper triangularity of the
coefficient block matrix and the fact that the matrices on the main diagonal are
identity matrices implies that the results are obtained with no matrix inversion.
The following two theorems hold for both the homogeneous and non-
homogeneous cases but only the homogeneous results will be given.
A straightforward proof of the randomness of the matrix
h
Φ is possible by
exploiting the following:
Theorem 3.2 The matrices ()
h
khΦ are stochastic.
Proof The result is true for (0)
h
=
Φ I . We suppose that it is true for
1, , k
τ
= … .We have to check what happens under these hypotheses for k+1.
From (1.11) the equation (3.19) becomes:
() ( )
()
1
1
(( 1) ) ( 1) (( 1 ) )
(( 1) ).
k
hhhh
h
kh h h k h
kh
τ
τ
ττ
+
=
+= − − +−
++
∑
Φ QQ Φ
D
(3.20)
To prove that (( 1) )
h
kh+Φ is stochastic we have to show that:
1
(( 1) ) 1, 1, , .
m
h
ij
j
kh i m
φ
=
+= =
∑
… (3.21)
An element of (3.20) is given by:
1
11
1
11
(( 1) ) (( 1) ) ( ) (( 1 ) )
(( 1) ) (( 1 ) ).
km
hh hh
ij ij il lj
l
km
hh
il lj
l
khdkh Qh k h
Qhkh
τ
τ
φτφτ
τφ τ
+
==
+
==
+= ++ +−
−−+−
∑∑
∑∑
(3.22)
Summing up with respect to j and taking into account relations (2.4), (1.8), (1.19)
and the inductive hypothesis, the following result is obtained:
1
11111
1
11 1
(( 1) ) 1 (( 1) ) ( ) (( 1 ) )
(( 1) ) (( 1 ) ) 1.
mmkmm
hhhh
ij ij il lj
jjlj
km m
hh
il lj
lj
kh Qkh Qh k h
Qh kh
τ
τ
φ
τφ τ
τφτ
+
=====
+
== =
+=− ++ +−
−− +−=
∑∑∑∑∑
∑∑ ∑
(3.23)
Now let Z be a continuous time HSMP with
Φ as evolution equation and
{
}
n
T
as sequence of the state change times.
If we set:
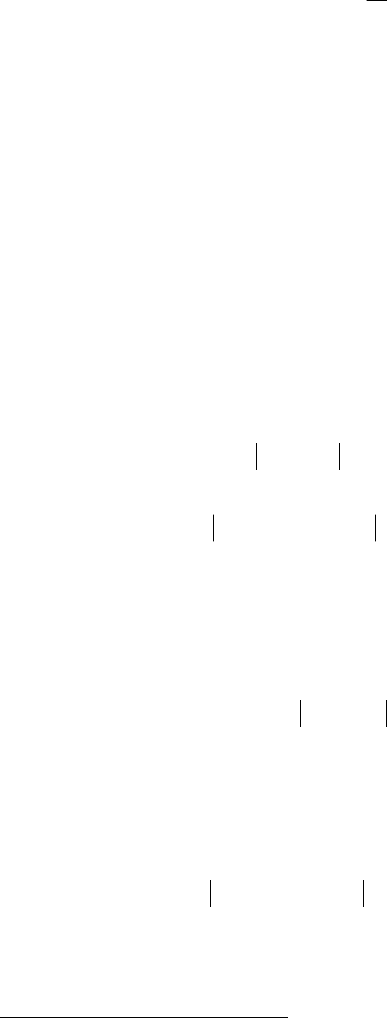
Discrete time SMP and numerical solution 141
n
h
n
T
Th
h
⎢
⎥
=
⎢
⎥
⎣
⎦
(3.24)
and
()
h
n
Z
tJ
=
if
1
hh
nn
TtT
+
≤< , (3.25)
then
h
Z
is a DTHSMP with evolution equations given by:
11
() () ()(( ))
mk
hh hh
ij ij il lj
l
kh d kh b h k h
τ
φτφτ
==
=+ −
∑∑
(3.26)
and it is defined on the same probability space
{
}
,,P
Ω
ℑ of Z.
Given
Ω∈
ω
the following result holds P-almost.
Theorem 3.3 The
h
Z
process converges to Z for 0h → in the Skorohod
topology
1
.
Proof It must be shown that 0T
∀
> there exists a time rescaling sequence
{
}
h
λ
where
h
λ
is a continuous, strictly increasing and surjective function from
[0, )+∞ to [0, )
+
∞ such that:
sup ( ) 0
h
tT
tt
λ
≤
−
→ if 0h → (3.27)
and
()
sup ( ) ( ) 0
hh
tT
ZtZt
λ
≤
−
→ if 0h → ; (3.28)
(see Ethier and Kurtz (1986)).
Obviously,
n
T →+∞ if n →+∞, (3.29)
then it is sufficient to verify that the proposition holds for
,.
n
TT n
=
∀
If we set:
10
min , 0
hh h
kk
lkn
hTTT
−
≤≤
<− =
, (3.30)
let
h
λ
be the linear function that transforms the intervals
[
]
1
,
kk
TT
−
into
[]
1
,
hh
kk
TT
−
with 1 kn≤≤ and
0
0T
=
, given by:
() ( ),
hn
hn n
tT tT tT
λ
=
+− ≥ . (3.31)
Then
{
}
h
λ
verifies the proposition's conditions and:
(()) () 0 .
hh
n
Z
tZt tT
λ
−=∀≤ (3.32)
Then
h
Z
converges to Z in the Skorohod topology with probability 1 and
therefore, in particular,
h
Z
converges in law, i.e. in the weak sense of stochastic
processes.
1
Skorokhod topology is the topology defined on the set of trajectories of stochastic
processes. For more details see (Billingsley (1968)).
142 Chapter 4
Remark 3.2 The weak convergence of stochastic processes is in reality the weak
convergence of their laws, where the laws are probability measures induced from
the processes on the space of their trajectories. In this case it is the space of right
continuous functions with left limits, in which the Skorokhod topology holds.
Finally it is to be observed that the
h
λ
sequence depends on
n
T
by means of
(3.30).
4 SOLUTION OF DTHSMP AND DTNHSMP IN THE
TRANSIENT CASE: A TRANSPORTATION EXAMPLE
4.1 Principle Of The Solution
Generally speaking it is clear that, for the purpose of application, it is more
worthwhile to solve systems (3.13) and (3.14) in a finite time horizon, which
means that the process is solved in the transient case.
In the following, an algorithm useful for solving both evolution equations is
briefly presented.
First of all, an epoch T is fixed and, in this light, equation (3.15) for both cases
becomes:
TT T
∗=U Φ D . (4.1)
The algorithms solve the linear system (4.1), in the sense that for known matrices
T
F and P, it determines the matrix of the unknown
T
Φ by means of two
iterative procedures. For the algorithms it is not necessary to compute the
U
matrix, but it is enough to construct the matrices
B whose elements are defined
respectively in (1.11) and (1.12).
The variables involved in the algorithms are:
INPUTS:
m, T,
P (embedded M.C.),
T
F
(Matrix of the increasing distribution function of
waiting times)
RESULTS:
T
Q ,
T
B ,
T
S ,
T
D ,
T
Φ
STEPS:
Reads m, T
Reads
P
Reads
T
F
Discrete time SMP and numerical solution 143
Constructs
T
Q
Constructs
T
B
Constructs
T
S
Constructs
T
D
Solves the system and finds
T
Φ
The steps are very general and hold in both cases. As we already said, the main
difference is given by the fact that in the homogeneous case the matrices are
lower triangular and upper triangular in the non-homogeneous case, see (3.16)
and (3.17).
For a complete description of algorithms respectively in homogeneous and non-
homogeneous cases, we refer to Corradi et al (2004) and Janssen-Manca (2001a).
4.2 Semi-Markov Transportation Example
4.2.1 Homogeneous Case
In this first example of a semi-Markov model, we extend to a semi-Markov
environment the transportation problem presented in section 9.6 of Chapter 2.
We consider that a taxicab driver will work for eight hours. So we will work in
the transient case within 32 time periods, which means that a period is a time
interval of 15 minutes. In this way we can consider the full working time of a
driver.
In this model, ( )
ij
t
φ
represents the probability that a driver who is in the state i
will be in the state j after a time t and we have to solve the evolution equation.
This example is really simple so all the steps that are necessary to solve the
DTHSMP could be shown.
The input is:
m = 3,
T = 32.
The matrix
P was given in the formula (9.108) of Chapter 2 but in real
application it could be constructed by data in the following way.
We are supposed to know all the runs that were driven in one month by all the
taxicab drivers, so we know for each run the starting zone, the arriving zone and
the course duration.
We refer to our case study, so we have three states, and we should construct the
transition matrix
P by the known data. We could construct a matrix A where
ij
a = number of runs from the zone i to the zone j in the month.
Then, it follows that:

144 Chapter 4
3
.
ij
ij
ik
k
a
p
a
=
∑
(4.2)
The matrix
[]
()
ij
F
t=F , the discrete time increasing probability distribution of
the waiting time in each state i given that the next state to be successively
occupied is j, should be constructed by the data.
The way to construct these d.f. by the data is the following.
We would construct for each i and j the related d.f.
(0), (1), (2), , (32)
ij ij ij ij
FFF F…
. (4.3)
From our data we compute the vector
((1),(2),,(32),(33))
ij ij ij ij ij
vv v v=v … (4.4)
where (1)
ij
v represents the number of all the runs that have a duration (including
also the waiting time of the taxi driver before beginning the run) less than or
equal to 15 minutes,
(2)
ij
v the number of all the courses that have a duration
greater than 15 minutes and less than or equal to 30 minutes and so on.
In
(33)
ij
v
there will be the number of all the runs from i and j that have a
duration larger than eight hours if any.
From the vector
ij
v we can construct the vector
ij
w :
1
() ( ) 1, ,33
t
ij ij
s
wt vs t
=
==
∑
… . (4.5)
So, we finally get the elements of the matrix
F:
()
(0) 0, ( ) , 1, ,32
(33)
ij
ij ij
ij
wt
FFt t
w
== =
… . (4.6)
To illustrate this method proposed for real data, we will here construct artifical
data and find matrix
F by means of pseudorandom generator numbers.
Our example is very simple (only three states) but with 32 time periods,
reporting of all the matrices involved in the computation will be too long and so
we will report for each matrix the time periods 1, 5, 10, 20, 30 and 32.
We get the following results:
Matrix
F
F(1) F(5) F(10)
0.0470 0.0396 0.0514 0.1835 0.1299 0.2349 0.2863 0.2581 0.3524
0.0200 0.0449 0.0009 0.1478 0.0847 0.0910 0.3083 0.2648 0.2924
0.0456 0.0168 0.0325 0.1314 0.1472 0.1106 0.2828 0.2491 0.3183
F(20) F(30) F(32)
0.5288 0.5628 0.6047 0.8268 0.8377 0.9236 0.8468 0.8574 0.9938
0.5877 0.4767 0.5842 0.8943 0.7982 0.8997 0.9423 0.8272 0.9382
0.5500 0.4956 0.6617 0.8721 0.8131 0.8376 0.9307 0.8478 0.9028
Discrete time SMP and numerical solution 145
Note that, always,
F(0)=0 because there are no movements in a time 0, and
F(32)<1 because it is the last time period and therefore a truncated d.f.
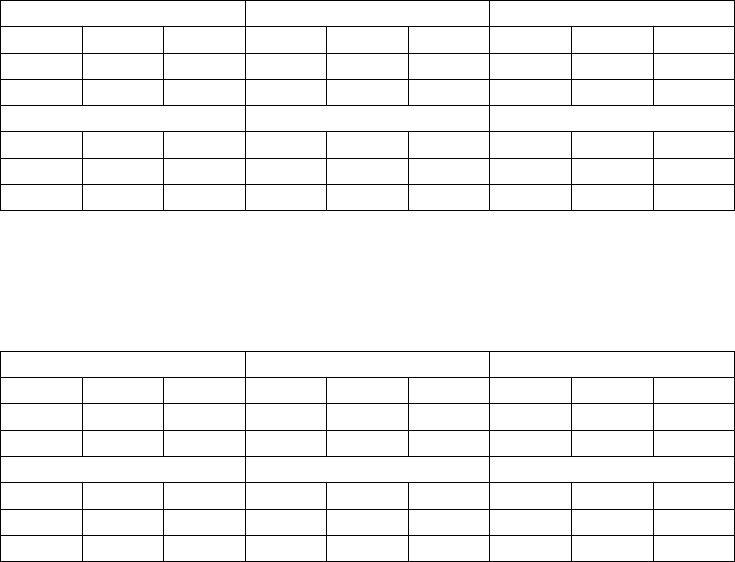
After the computation of matrix
F, we can compute the kernel Q as follows (see
relation (1.15))
() ()tt
=
⋅QFP, (4.7)
where the symbol
⋅ means matrix product element by element.
Matrix
Q
Q(1) Q(5) Q(10)
0.0235 0.0158 0.0051 0.0918 0.0520 0.0235 0.1432 0.1032 0.0352
0.0060 0.0269 0.0001 0.0443 0.0508 0.0091 0.0925 0.1589 0.0292
0.0091 0.0017 0.0227 0.0263 0.0147 0.0775 0.0566 0.0249 0.2228
Q(20) Q(30) Q(32)
0.2644 0.2251 0.0605 0.4134 0.3351 0.0924 0.4234 0.3430 0.0994
0.1763 0.2860 0.0584 0.2683 0.4789 0.0900 0.2827 0.4963 0.0938
0.1100 0.0496 0.4632 0.1744 0.0813 0.5863 0.1861 0.0848 0.6319
The next matrix to be computed is the matrix
B using the following result:
if 0,
()
() ( 1) if 0.
t
t
tt t
=
⎧
=
⎨
−
−>
⎩
0
B
QQ
(4.8)
Matrix
B
B(1) B(5) B(10)
0.0235 0.0158 0.0052 0.0194 0.0061 0.0046 0.0061 0.0079 0.0032
0.0060 0.0269 0.0001 0.0029 0.0153 0.0009 0.0095 0.0303 0.0040
0.0091 0.0017 0.0227 0.0110 0.0023 0.0257 0.0009 0.0006 0.0331
B(20) B(30) B(32)
0.0222 0.0151 0.0000 0.0083 0.0097 0.0034 0.0062 0.0059 0.0053
0.0033 0.0138 0.0045 0.0067 0.0251 0.0048 0.0128 0.0047 0.0034
0.0038 0.0011 0.0020 0.0115 0.0045 0.0040 0.0078 0.0013 0.0240
Let us just mention that the 0 in position
1,3
(20)b is a numerical zero in the sense
that rounding this number at the fourth decimal gives 0.
Then, we have to compute the estimation of matrix
H, whose elements are the
following, see relation (1.8):
1
0if ,
()
() if .
m
ij
ik
k
ij
Ht
Qt i j
=
≠
⎧
⎪
=
⎨
=
⎪
⎩
∑
(4.9)
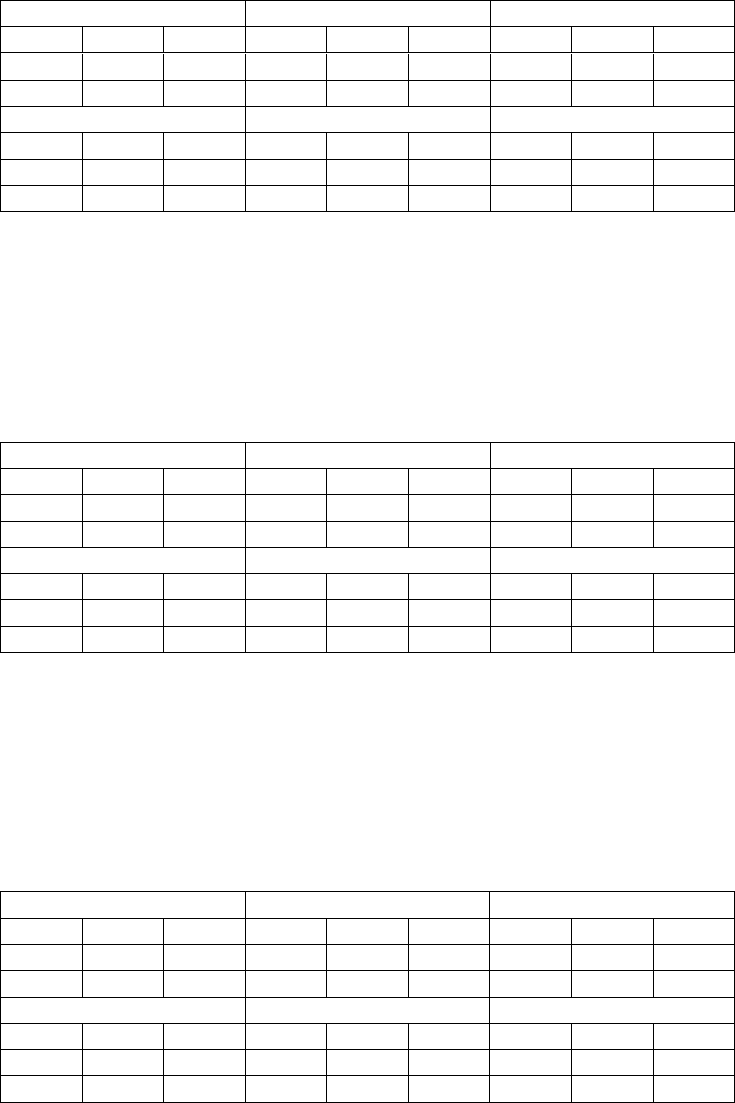
146 Chapter 4
0 0.0330 0 0 0.1043 0 0 0.2806 0
0 0 0.0335 0 0 0.1184 0 0 0.3043
H(20) H(30) H(32)
0.5500 0 0 0.8408 0 0 0.8658 0 0
0 0.5207 0 0 0.8372 0 0 0.8728 0
0 0 0.6228 0 0 0.8421 0 0 0.9028
We know that these elements represent the probability to leave the state i in a
period less than or equal to the period t, and so have sense only in the main
diagonal of each submatrix.
The next matrix
D,whose elements represent the probability of remaining in the
state for t periods, is given by
() ()tt
=
−DIH. (4.10)
We get:
Matrix
D
D(1) D(5) D(10)
0.9555 0 0 0.8328 0 0 0.7184 0 0
0 0.9670 0 0 0.8957 0 0 0.7194 0
0 0 0.9665 0 0 0.8816 0 0 0.6957
D(20) D(30) D(32)
0.4500 0 0 0.1592 0 0 0.1342 0 0
0 0.4793 0 0 0.1628 0 0 0.1272 0
0 0 0.3772 0 0 0.1579 0 0 0.0972
The matrix we look for, that is
Φ , is the solution of the evolution equation of the
DTHSMP.
Here, ( )
ij
t
φ
represents the probability that a taxicab driver being at time 0 in
zone i will be after t periods, in the state j.
From the results given below, any row of the submatrix ( )t
Φ is indeed a
probability distribution.
The results are:
Matrix
Φ
Φ (1) Φ (5) Φ (10)
0.9790 0.0158 0.0052 0.9228 0.0530 0.0242 0.8553 0.1065 0.0382
0.0060 0.9939 0.0001 0.0437 0.9465 0.0098 0.0916 0.8767 0.0317
0.0091 0.0017 0.9892 0.0264 0.0154 0.9582 0.0582 0.0288 0.9130
Φ (20) Φ (30) Φ (32)
0.6973 0.2320 0.0707 0.5337 0.3490 0.1173 0.5132 0.3587 0.1281
0.1767 0.7548 0.0685 0.2745 0.6116 0.1139 0.2902 0.5882 0.1216
0.1220 0.0686 0.8094 0.2039 0.1278 0.6683 0.2196 0.1386 0.6418
Matrix
H
H(1) H(5) H(10)
0.0445 0 0 0.1672 0 0 0.2816 0 0
