Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability
Подождите немного. Документ загружается.


Markov renewal processes
107
Proposition 14.1 (Basic properties of (J,X) processes)
(i) The process
()
(,), 0
nn
JS n≥ is a Markov process with I
×
as state space;
more precisely, we have a.s. for all j of I and all real x:
(
)
1
, ( , ), 0,1,..., 1 ( ).
n
nn kk Jjn
PJ jS x J S k n Q x S
−
=≤ = −= −
(14.4)
(ii) The process
()
(), 0
n
Jn≥ is a homogeneous Markov chain with I as state
space; more precisely, we have a.s. for all j of I:
()
1
, , 0,1,..., 1 .
n
nk Jj
PJ jJ k n p
−
==−= (14.5)
(iii) For all strictly positive n and for all real x, we have:
(
)
()
()
1
1
1 1
1
1
1
, , 0,1,..., 1 ( ), 0, ,
, , 0,1,..., ( ), 0, ,
,..., , , 0,1,..., ( ),
(0 , , 1,..., ).
n
nn
lnn
ii
nk J
nk JJ
k
nnlk kJJi
i
ki
PX xJ k n H x n x
PX xJ k n F x n x
PX x X x J k n F x
nnxik
−
−
−
=
≤=−= >∈
≤= = >∈
≤≤= =
<<< ∈ =
∏
(14.6)
Of course, probabilities p
ij
, i,j=1,…,m, and functions H
j
, j=1,…,m, F
ij
, i,j=1,…,m
are defined exactly as in relations (2.3) and (3.11).
The last relation in (14.6) shows the conditional independence of
1
,...,
k
nn
X
X given
11
1
, ,...,
k
nn n
J
JJ
−
.
From the relation (3.11) saying that:
1
1
1
1
()
,0,
()( ( , ))
(), 0,
()( ( )) (),
ij
ij
ij
ij n n n
ij
m
inn ijij
j
Qx
p
p
Fx PX xJ iJ j
Uxp
Hx PX xJ i pFx
−
−
=
⎧
>
⎪
=≤===
⎨
⎪
=
⎩
=≤==
∑
(14.7)
it is clear that a (J,X) process is completely defined by either the pair
(
)
,pQ or
by the triple
(
)
,,pPF where:
1
( ,... ), , , .
mij ijij
p
pQpF
⎡
⎤⎡⎤⎡⎤
====
⎣
⎦⎣⎦⎣⎦
pQPF (14.8)
15 FUNCTIONALS OF (J-X) PROCESSES
This section introduces the concept of functional W of a given (J,X) process,
fundamental for a lot of applications not only in finance and insurance but also in
operations research.
To define the functional W, we introduce a real and Lebesgue measurable
function f of three variables defined on the set II
×
× .
108 Chapter 3
When they exist, we will use the following notation for the expectations with
,ik I∈ :
(2) 2
(2) (2)
11
(,,) (), (,,) (),
,.
ik
iik
ik ik ik
mm
iik
kk
f
ikxdQ x f ikxdQ x
ξξ
ξξξ ξ
==
==
==
∫∫
∑∑
(15.1)
Definition 15.1 Given a (J,X) process
(
)
(, ), 0
nn
JX n≥ defined by
(
)
,pQ , and a
Lebesgue measurable real function f on I I
×
× , the functional W
f
is defined as
the stochastic process
( ( ), 0,1,...)
ff
WWnn
=
= (15.2)
where
1
1
0, 0,
()
(,,),0.
n
f
kkk
k
n
Wn
fJ J X n
−
=
=
⎧
⎪
=
⎨
>
⎪
⎩
∑
(15.3)
Janssen (1969b) extended to functionals of (
J,X) processes key results obtained
by Pyke and Schaufele (1964) for functionals of positive (
J,X) processes: the
strong law of large numbers ( in short SLLN) and the Central Limit Theorem (in
short CLT).
The basic idea of the proofs is to decompose the sum
W
f
(n) by introducing return
times of return indices for the embedded Markov chain supposed to be ergodic
()
,0
n
Jn≥ defined by relations (9.44), (9.45) and (9.47) in Chapter 2, that is for
all
j belonging to I:
{}
()
0
() () ()
01 1 0
0,
sup : , , , .
j
jjj
nnln
k
r
rkkrJjrlln
−−
=
=∈> ≠<<∈
(15.4)
We know that the assumption of ergodicity implies that all states are positive
recurrent so that, for all
j,
()j
n
nr→∞⇒ →∞. (15.5)
Moreover, if for all
j we introduce the stochastic process in discrete time:
(
)
()
,0
j
s
un> (15.6)
with
()
1
()
()
1
1
(,,)
j
s
j
s
r
j
s
nnn
nr
ufJJX
+
−
=+
=
∑
, (15.7)
then it is clear that this process (15.7) is a sequence of independent and
identically distributed r.v. with values in
, that is a random walk on the real
line.

Markov renewal processes
109
The following important propositions give some results concerning the moments
of r.v.
10
,,
j
ujIJ j∈=and the fundamental Strong law of large numbers for (J,X)
processes.
Proposition 15.1 If the embedded Markov chain of the considered (J,X) process
is ergodic and if the considered functional is such that the expectations
(2)
,
ii
ξ
ξ
exist for all i belonging to I, then
(
)
(
)
() () 2
11
,( )
jj
E u E u exist and are given by:
()
()
()
1
1
() 2 (2)
1
11
1
(),
12
() ( ) ,
m
j
ii jj
i
j
mm
j
i i i r kj jr kr ik r
iikjrj
jj
Eu
Eu m m m
πξ μ
π
π
ξππ ξξ
ππ
=
==≠≠
==
=+ +−
∑
∑∑∑∑
(15.8)
mean return times in the embedded MC ,,,
ls
ml sls I
≠
∈ being given by relations
(9.42) of Chapter 2.
Proposition 15.2 (Strong law of large numbers for functionals of (J,X)
processes)
For any ergodic (J,X) process so that the conditional means ,,
ij
bij I
∈
are finite,
we have the following result:
1
()
,..
m
f
ii
n
i
Wn
as
n
πξ
→∞
=
⎯⎯⎯→
∑
(15.9)
The next results are related to a central limit theorem for functionals of (J,X)
processes.
Proposition 15.3 (Central limit theorem for functionals of (J,X) processes)
If the expectations
i
ξ
exist for all i belonging to I, we have in the ergodic case
and for the convergence in law that:
1
()
0, var .
j
f
jj j
n
jj
m
Wn n
mm
Nuf
m
n
→∞
−
⎛⎞
⎛⎞
→−
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
(15.10)
Moreover, if
j
j
μ
defined by the first relation of (15.8) is non-null, then
()
(0, )
ff
g
n
Wn nA
N
B
n
μ
μ
→∞
−
⎯⎯⎯→
(15.11)
where
110 Chapter 3
1
1
1
(2) *
*
,
,
1
2,
,, ,
m
ii
i
m
ii
i
f
m
ii
i
fiiiikrjkr
iikjrj
ii
i
kj jr kr
jkr
rr
A
Bp
mmm
pijkI
m
μπη
πξ
πη
πξ πξ ξ
πη
=
=
=
≠≠
=
=
⎛⎞
=+
⎜⎟
⎝⎠
+−
=∈
∑
∑
∑
∑∑∑∑
∑
(15.12)
and
1
var
j
j
j
m
uf
m
⎛⎞
−
⎜⎟
⎜⎟
⎝⎠
represents the variance of the function
1
j
u defined by the
relation (15.7) but here related to the function
()
j
j
j
m
f
m
−
.
Remark 15.1 It can be proved that A
f
and B
f
are independent of state j.
Proposition 15.4 (Central limit theorem for the two-dimensional process
()
,(), 0
nf
JW nn≥ )
If the expectations
i
ξ
exist for all i belonging to I, we have in the ergodic case
and for the convergence in law that:
()
,(),
ff
nk
Wn nA
PJ k x x
n
μ
π
−
⎛⎞
=≤=Φ
⎜⎟
⎝⎠
(15.13)
where the function Φ is the distribution function of the normal law (0, )
g
N
B
μ
.
Remark 15.2 An immediate consequence of this last proposition is that
processes ( , 0)
n
Jn≥ and ( ( ), 0)
f
Wnn≥ are asymptotically independent.
These last two propositions immediately give the following one for the special
case of (J,X) processes
Proposition 15.5 (Central limit theorems for the two-dimensional (J,X)
processes)
For any ergodic (J,X) process such that the conditional variances
2
ij
σ
related to
the conditional d.f. ,,
ij
F
ij I∈ are finite, we have the following results:

Markov renewal processes
111
(0, ),
n
g
n
Sn
N
B
n
μ
μ
→∞
−
⎯⎯⎯→
(15.14)
,(),
n
nk
Sn
PJ k x x
n
μ
π
−
⎛⎞
=≤=Φ
⎜⎟
⎝⎠
(15.15)
where the function Φ is the distribution function related to the normal law
()
0,
g
N
B
μ
with here, for all i and k belonging to I:
()
1
2
(2) 2 2 2
11
(,,) ,
,,
()2 ,
m
ii
i
ik ik ik i i
mm
ik ik ik ik i i ik i i ik
ii
gikx x
pb
p
bpp
πη
ξξη
ξ σ πη πη
=
==
=−
==
⎛⎞⎛⎞
=−− +
⎜⎟⎜⎟
⎝⎠⎝⎠
∑
∑∑
(15.16)
2
(, )
ik
ik I
σ
∈ being the conditional variance related to the conditional distribution
(, )
ik
F
ik I∈ .
16 FUNCTIONALS OF POSITIVE (J-X) PROCESSES
It is clear that all the results of the preceding paragraph are valid for the special
case of positive (J,X) processes for which the r.v. X
n
are a.s. non-negative.
But moreover instead of considering the sum of the first n transitions to define
W
f
(n) in relation (15.3) we can reinsert the time with a sum up to N(t), that is the
total number of transitions in the semi-Markov process related to the considered
semi-Markov kernel
Q.
In fact , this was the case originally considered by Pyke and Schaufele (1964) so
that now, relation (15.3) takes the form:
()
1
1
0, ( ) 0,
()
(,,),()0.
Nt
f
nnn
k
Nt
Wt
fJ J X Nt
−
=
=
⎧
⎪
=
⎨
>
⎪
⎩
∑
(16.1)
These authors proved the next proposition corresponding to the strong law of
large numbers and central limit theorem of the preceding sections.
Proposition 16.1 (Strong law of large numbers for functionals of positive (J,X)
processes)
If the expectations
i
ξ
exist for all i belonging to I, we have in the ergodic case
that:
()
,..,
fj
t
jj
Wt m
as
tm
→∞
⎯⎯⎯→
(16.2)
with:
112 Chapter 3
1
1
,
,
m
j
ii
i
m
j
jii
i
m
m
π
ξ
π
η
=
=
=
=
∑
∑
(16.3)
the limit ratio /
j
jj
m m being still independent of j .
The propositions related to the central limit theorem have similar extensions for n
replaced by N(t) to the numerator and by t to the denominator.
17 CLASSICAL RANDOM WALKS AND RISK THEORY
17.1 Purpose
In the beginning of this chapter, we focused our attention on semi-Markov chains
defined by a positive (J,X) process. The case of an extended semi-Markov chain
is considered in section 14 starting from a general (J,X) process and having a
very different interpretation, directly related to the classical notion of random
walk.
In the next subsections, we will recall some basic notions concerning random
walks that will be extended to the main results of what will be called Markov
random walks in the next section.
After that, we will develop the main classical models in risk theory, which is very
useful for insurance companies.
17.2 Basic Notions On Random Walks
Let
(
)
,1
n
Xn≥ be i.i.d. random variables, with F as common d.f., such that:
F(0) < 1, (17.1)
F(0) > 0. (17.2)
These two relations imply that for all n, the events
{
}
{
}
:0,:0
nn
XX
ωω
>< (17.3)
have strictly positive probabilities.
As usual, let us define the following r.v.:
00
0, a.s.SX
=
= , (17.4)
0
n
nk
k
SX
=
=
∑
. (17.5)
We can now give the following basic definition:
Markov renewal processes
113
Definition 17.1 The random sequence
(
)
,0
n
Sn≥ is called a random walk
starting at x
0
, whose
()
,1
n
Xn≥ are the successive steps.
If x
0
=0, the random walk is said to start at the origin.
Example 17.1 If the distribution of r.v. X
n
is concentrated on a two-point set
{
}
1,1− with
(1),(1)(1),
nn
pPX q p PX===−=≠ (17.6)
then the associated random walk is called the simple random walk or the
Bernoulli random walk.
The interpretation is quite simple: let us consider for instance a physical particle
moving on a straight line starting at the origin.
This particle takes a first unit step to the right with probability p or to the left
with probability q and so on.
Clearly, the r.v. S
n
will give the position of the particle on the line after the nth
step.
Though very particular, the notion of a simple random walk has a lot of
important applications in insurance, finance and operations research. A very
classical application is the so-called gambler's ruin problem.
Let us consider a game with two players such that at each trial, each gambler
wins 1 monetary unit with probability p and loses 1
−
monetary unit with
probability ( 1 )qp
=
− .
If u is the initial "fortune" of one player, he will be ruined at trial n iff, for the
first time, his fortune just after this trial becomes strictly negative.
He will be ruined before or at trial n iff he is ruined at one time k, k
≤ n.
The probability of this last event will be noted by
(,)un
Ψ
and the probability of
being ruined precisely at time n will be noted by
(,)un
υ
.
Clearly, we have:
0
(,) (, )
n
k
un uk
υ
=
Ψ=
∑
(17.7)
and
(,) (,) (, 1).un un un
υ
=
Ψ−Ψ− (17.8)
The probability of not being ruined on
[
]
0, n , that is to say after any trial on
[]
0, n , will be represented by ( , )un
γ
, and of course, we have:
(,) 1 (,)un un
γ
=
−Ψ . (17.9)
Probabilities ( , )un
γ
and
(,)unΨ
are called respectively the non-ruin probability
and the ruin probability on
[]
0, n starting at time 0 with an initial fortune - also
called reserve or equities for insurance companies - of amount u.
114 Chapter 3
Now we will see how to express these two probabilities with the aid of events as
functions of the variables X
n
, n=0,1,.. representing the "gain" (positive or
negative) of the considered player just after the nth trial.
Starting with x
0
=u, we can write:
(
)
( , ) 0, 1,..., 1, 0
kn
un P S k n S
υ
=>=−<. (17.10)
If we introduce now the discrete r.v. T defined as follows:
{
}
inf : 0
n
TnS
=
< , (17.11)
we get:
(
)
(,)un PT n
υ
=
= , (17.12)
(
)
(,)un PT n
Ψ
=≤, (17.13)
(
)
(,)un PT n
γ
=
> . (17.14)
One of the major problems in the so-called risk theory is that of giving explicit
results about these three probabilities. This part of risk theory is called the ruin
problem and it is equivalent to studying the distribution of the stopping time T.
It is recalled in Janssen and Manca (2006) that the main concepts in random walk
theory are those of ladder variables. To be self-contained, let us briefly give the
following basic
Definition 17.2.
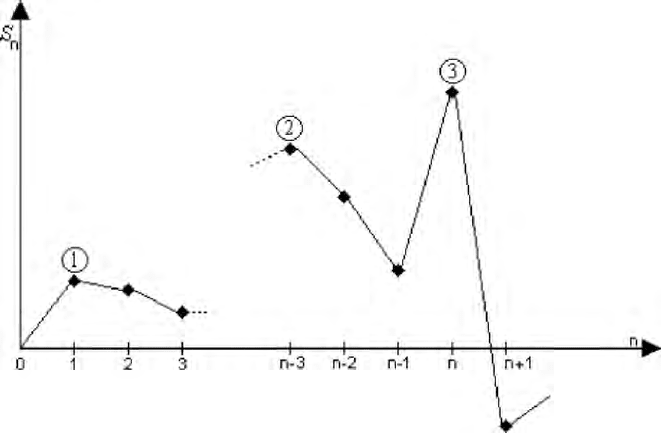
Graphically, ladder epochs and ladder heights are clearly seen on trajectories
given in a two-dimensional graph where points are designated by the coordinates
{
}
(, ), 0
n
nS n≥ .
Figure 17.1: ladder trajectory

Markov renewal processes
115
In the graph of Figure 17.1, we have joined the points of coordinates
1
(, ),( 1, )
kk
kS k S
+
+
in order to clearly show the evolution of the process.
For example, in the trajectory of
Figure 17.1, we have the strictly ascending
ladder points
(
)( )
(
)
13
1, , 3, , ,
nn
Sn S nS
−
− and the strictly descending ladder points
()()
11
1, , 1,
nn
nS nS
−+
−+.
The next definitions formalise these concepts of ladder variables. We follow the
presentation of Feller (1971) but without the assumption that x
0
=0.
Definition 17.2 The first (strict) ascending ladder point
(
)
11
, HΓ is the first term
of the sequence
()
()
,,0
n
nS n> for which S
n
is strictly superior to S
0
. That is:
{
}
{
}
110100
::,...,,
nn
nSSSSSS
ωω
−
Γ= = ≤ ≤ > . (17.15)
The r.v.
1
Γ is called the first strict ladder epoch and the r.v. defined by
1
111
,HS
ξ
ξ
=
=Γ (17.16)
is called the first strict ladder height.
The possibly defective bi-dimensional distribution of
(
)
11
, HΓ will be noted by
(
)
{
}
11
() , , 0,
n
Hx P nH xn x
+
=Γ= ≤ > ∈ +∞∪ . (17.17)
Consequently, we obtain:
(
)
1
()
n
PnH
Γ
== +∞, (17.18)
()
1
1
()( ())
n
n
PH x H x Mx
∞
=
≤= =
∑
, (17.19)
so that both r.v.
11
,
H
Γ have the same defect; that is:
()
(
)
11
1().PPH MΓ=∞= =∞= − ∞ (17.20)
17.3 Classification Of Random Walks
This section is devoted to a very important result known as the classification of
random walks. Briefly, this result states that only two possibilities exist for the
asymptotic behaviour of the random walk
(
)
,0
n
Sn≥ .
Either:
(
)
(
)
limsup liminf 1
nn
PSPS
=
∞= =−∞= (17.21)
or:
(
)
lim or lim 1
nn
PS S
=
∞=−∞=. (17.22)
In the first case, the random walk is called oscillating; in the
second, it is said to
drift to or -+∞ ∞ .
In this last possibility, we have a.s.

116 Chapter 3
lim
n
S
=
+∞ (17.23)
or
lim
n
S
=
−∞ . (17.24)
Proposition 17.1 There exist only two types of random walks:
(1) the oscillating type: both ascending and descending renewal processes of
ladder heights are persistent. In this case, the process
(
)
,0,1,
n
Sn= … oscillates
with probability 1 between
−∞ and
+
∞ , and:
(
)
(
)
11
D
EE
Γ
=Γ=∞; (17.25)
(2) drift toward
±∞ : in the case of
−
∞ , the ascending renewal process is
terminated and the descending renewal process is proper with probability 1. The
process
(
)
,0,1,
n
Sn= … drifts with probability 1 toward
−
∞
and reaches a finite
non-negative maximum. M; moreover:
()
1
111
() .
111()
D
E
M
ς
ζζ
Γ= ∞=
−
−−∞
(17.26)
And if M is the r.v. defined as
01
max( , ,..., ,...),
n
MSSS
=
(17.27)
then
()(1())()PM x M x
ς
≤
=− ∞ . (17.28)
The results are analogous in the case of a drift toward
+
∞ .
In fact, when the mean
μ
of the r.v. X
n
, n>1 exists, the strong law of large
number asserts that, a.s.:
lim ,
n
n
S
n
μ
→∞
=
(17.29)
so that we immediately get the following results:
0lim ,
0lim .
n
n
n
n
S
S
μ
μ
→∞
→∞
>⇒ =+∞
<
⇒=−∞
(17.30)
The next theorem gives the complete relation, including the case 0
μ
= which is
more difficult to treat.
Proposition17.2 If the mean
μ
of the r.v. X
n
, n>1 exists, then:
(i)
μ
=0 implies that the random walk is oscillating,
(ii)
μ
>0 implies that the random walk drifts toward +
∞
,
(iii)
μ
<0 implies that the random walk drifts toward -
∞
.
In fact, it can also be proved that the converse is true, and so we have:
