Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability
Подождите немного. Документ загружается.

Chapter 3
MARKOV RENEWAL PROCESSES, SEMI-
MARKOV PROCESSES AND MARKOV
RANDOM WALKS
In this chapter, the reader will find the main definitions and results on Markov
renewal processes, semi-Markov processes and Markov random walks useful for
understanding of the main applications in finance, insurance and reliability
developed in the next chapters. A full presentation including the proofs of the
theorems recalled here can be found in Janssen-Manca
(2006) (chapter 4 to
chapter 6).
1 POSITIVE (J-X) PROCESSES
Let us consider a physical or economic system called S with m possible states, m
being a finite natural number.
For simplicity, we will note by I the set of all possible states:
{
}
1,...,Im= (1.1)
as we already did in Chapter 2 partially devoted to Markov chains.
At time 0, the system S starts from an initial state represented by the r.v. J
0
, stays
a non-negative random length of time X
1
in this state, and then goes into another
state J
1
for a non-negative length of time X
2
before going into J
2
, and so on.
So we have a two-dimensional stochastic process in discrete time called a
positive (J-X) process:
()((,),0)
nn
JX JXn
−
=≥ (1.2)
supposing
0
0, . .
X
as
=
(1.3)
where the sequence ( , 0)
n
Jn≥ gives the successive states of S in time and the
sequence
(, 0)
n
Xn≥ gives the successive sojourn times.
More precisely, X
n
is the time spent by S in state J
n-1
(n>0).
Times at which transitions occur are given by the sequence
(, 0)
n
Tn≥ where:
011
1
0, ,...,
n
nr
r
TTXT X
=
== =
∑
(1.4)
and so
1
,1
nnn
X
TTn
−
=
−≥. (1.5)

78 Chapter 3
2 SEMI-MARKOV AND EXTENDED SEMI-MARKOV
CHAINS
On the complete probability space ( , , )P
Ω
ℑ , the stochastic dynamic evolution of
the considered (J-X) process will be determined by the following assumptions:
P(X
0
=0)=1, a.s.,
P(J
0
=i)=p
i
, i=1,…,m with
1
1
m
i
i
p
=
=
∑
, (2.1)
for all n>0, j=1,…,m, we have:
1
( , ( , ), 0,..., 1) ( ), . .
n
nnkk Jj
PJ jX x J X k n Q x as
−
=≤ = −= (2.2)
where any function Q
ij
(i,j=1,…,m) is a non-decreasing real function null on
+
such that if
lim ( ), ,
ij ij
x
p
Qx ij I
→+∞
=
∈ , (2.3)
then:
1
1,
m
ij
j
p
iI
=
=
∈
∑
. (2.4)
With matrix notation, we will write:
1
, ( ( )), ,..., )
ij ij m
Qp (pp
⎡⎤ ⎡⎤
===∞=
⎣⎦ ⎣⎦
QP Qp . (2.5)
This leads to the following definitions.
Definition 2.1 Every matrix mm
×
Q of non-decreasing functions null on
+
satisfying properties (2.3) and (2.4) is called a semi-Markov matrix or a semi-
Markov kernel.
Definition 2.2 Every couple (p,Q) where Q is a semi-Markov kernel and p a
vector of initial probabilities defines a positive (J,X) process
(J,X) =((J
n
,X
n
), 0≥n ) with I
+
×
as state space, also called a semi-Markov chain (
in short a SMC).
Sometimes, it is useful that the random variables
,0
n
Xn≥
take their values in
instead of
+
, in which case we need the next two definitions.
Definition 2.3 Every matrix mm
×
Q of non-decreasing functions satisfying
properties
(2.3) and (2.4) is called an extended semi-Markov matrix or an
extended semi-Markov kernel.
Definition 2.4 Every couple (p,Q) where Q is an extended semi-Markov kernel
and
p a vector of initial probabilities defines a (J,X) process (J,X) =((J
n
,X
n
),

Markov renewal processes
79
0n ≥ ) with
I
×
as state space, also called an extended semi-Markov chain (in
short an ESMC).
Let us come back to the main condition (2.2); its meaning is clear. For example
let us suppose that we observe for a certain fixed n that J
n-1
=i, then the basic
relation (2.2) gives us the value of the following conditional probability:
1
( , ( , ), 0,..., 1, ) ( ).
nnkk n ij
PJ jX x J X k n J i Q x
−
=≤ = −== (2.6)
That is, the knowledge of the value of J
n-1
suffices to give the conditional
probabilistic evolution of the future of the process whatever the values of the
other past variables might be.
According to Kingman (1972), the event
{
}
1
:()
n
J
i
ωω
−
=
is regenerative in the
sense that the observation of this event gives the complete evolution of the
process in the future as it could evolve from n=0 as i the initial state.
(J-X) processes will be fully developed in section 14.
Remark 2.1 The second member of the semi-Markov characterisation property
(2.2) does not depend explicitly on n; also we can be precise that we are now
studying homogeneous semi-Markov chains in comparison with the non-
homogeneous case where this dependence with respect to n is valid.
3 PRIMARY PROPERTIES
We will start by studying the marginal stochastic processes ( , 0),
n
Jn≥
(, 0)
n
Xn≥ called respectively the J-process and the X-process.
(i) The J-process
From the semi-Markov relation (2.2) and Lebesgue’s theorem (see Chapter 1,
Proposition 4.1)), we deduce that a.s.:
1
((,),0,...,1) ()
n
nkk Jj
PJ j J X k n Q
−
==−=+∞. (3.1)
Using the smoothing property (see Chapter 1,
Proposition 6.2) of conditional
expectation, we get
1
( ( ), 0,..., 1) ( ( ) ( ), 0,..., 1),
n
nk Jj k
PJ j J k n EQ J k n
−
=
=−= +∞ =− (3.2)
and as the r.v.
)(
1
+∞
−
jJ
n
Q is ( , 0,... 1)
k
Jk n
=
− ,k=0,…,n-1)-measurable, we
finally get from relation (2.3) that:
1
( ( ), 0,..., 1)
n
nk Jj
PJ j J k n p
−
==−=
. (3.3)
Since relation (2.4) implies that the matrix
P is a Markov matrix, we have thus
proved the following result.

80 Chapter 3
Proposition 3.1 The J-process is a homogeneous Markov chain with P as its
transition matrix.
That is the reason why this J-process is called the imbedded Markov chain of the
considered SMC in which the r.v. J
n
represents the state of the system S just after
the nth transition.
From results of Chapter 2,
Corollary 9.1, it follows that in the ergodic case there
exists one and only one stationary distribution of probability
1
( ,..., )
m
π
π
=π
satisfying:
1
1
, 1,..., ,
1
m
ijji
j
m
i
i
p
jm
ππ
π
=
=
==
=
∑
∑
(3.4)
such that
()
0
lim ( )( lim ) , , ,
n
nijj
nn
PJ jJ i p i j I
π
→∞ →∞
=== = ∈ (3.5)
where we know from Chapter 2, relation (9.17) that
()nn
ij
p
⎡⎤
=
⎣⎦
P . (3.6)
(ii) The X-process
Here, the situation is entirely different because the distribution of X
n
depends on
J
n-1
. Nevertheless, we have an interesting property of conditional independence,
but before giving this property we must introduce some definitions.
Definition 3.1 The two conditional probability distributions
1
1
1
1
() ( , ),
() ( )
nn
n
JJ n n n
Jnn
F
xPX xJ J
HxPXxJ
−
−
−
−
=≤
=≤
(3.7)
are respectively called the conditional and unconditional distributions of the
sojourn time X
n
.
From the general properties of conditioning recalled in Chapter 1, section 6.2, we
successively get
(
)
1
-1
-1
-1
-1
1
1
() ( ( , ), 1, ) ,
()
,
()
,
nn
nn
nn
nn
nn
J
Jnkknnn
JJ
nn
JJ
JJ
JJ
F
xEPX xJXkn JJJ
Qx
EJJ
p
Qx
p
−
−
−
=≤ ≤−
⎛⎞
=
⎜⎟
⎜⎟
⎝⎠
=
(3.8)
provided that
1nn
J
J
p
−
is strictly positive. If not, we can arbitrarily give to (3.8) for
example the value U
1
(x) defined as
Markov renewal processes
81
1
0, 0,
()
1, 0.
x
Ux
x
<
⎧
=
⎨
≥
⎩
(3.9)
Moreover, from the smoothing property, we also have:
11
11
11
1
()( ( )) ( () )
( ).
nnn
nn nn
JnnJJn
m
JJ JJ
j
HxPXxJ EF xJ
p
Fx
−−
−−
−−
=
=≤ =
=
∑
(3.10)
We have thus proved the following proposition.
Proposition 3.2 As a function of the semi-kernel Q, the expressions conditional
and unconditional distributions of the sojourn time X
n
are given by:
1
1
1
1
()
,0,
()( ( , ))
(), 0,
()( ( )) ().
ij
ij
ij
ij n n n
ij
m
inn ijij
j
Qx
p
p
Fx PX xJ iJ j
Uxp
Hx PX xJ i pFx
−
−
=
⎧
>
⎪
=≤===
⎨
⎪
=
⎩
=≤==
∑
(3.11)
Remark 3.1
(i) From the last relation (3.11), we can also express the kernel Q as a function of
the F
ij
, i,j=1,…,m:
() (),, ,
i j ij ij
Qx pFxijIx
+
=∈∈ . (3.12)
So, every SMC can also be characterised by the triple (
p,P,F) instead of the
couple (
p,Q) where the mm× matrix F is defined as
ij
F
⎡
⎤
=
⎣
⎦
F
and the functions
,, 1, ,
ij
F
ij m= … are distribution functions on support
+
.
(ii) We can also introduce the means related to these conditional and
unconditional distribution functions.
When they exist we will write
( ), , 1,..., ,
( ), 1,...,
ij i j
R
ii
R
x
dF x i j m
xdH x i m
β
η
==
==
∫
∫
(3.13)
and the last relation (3.11) leading to the relation:
1
m
iijij
j
p
η
β
=
=
∑
. (3.14)
The quantities
ij
β
, i,j=1,…,m and
i
η
,i=1,…,m are respectively called the
conditional and unconditional means of the sojourn times.

82 Chapter 3
We can now give the property of conditional independence.
Proposition 3.3 For each integer k, let n
1
,n
2
,…,n
k
be k positive integers such that
n
1
<n
2
< <n
k
and
1
,...,
k
nn
x
x are k real numbers. Then we have:
(
)
11 11
11 1
11
11
,..., , ,..., ,
()... (),
kk kk
nn nn k
kk
nn n nnn n n
JJ n JJ n
PX x X x J J J J
FxFx
−−
−−
≤≤
=
(3.15)
that is the k random variables
1
,...,
k
nn
X
X are conditionally independent given
11
11
, ,..., ,
kk
nn n n
J
JJJ
−−
.
(i) The T-process
By relation (1.4), the sequence ( , 0)
n
Tn≥ represents successive renewal epochs,
that is, times at which transitions occur.
By analogy with renewal theory, we have the following definition.
Definition 3.2 The two-dimensional process (( , ), 0)
nn
JT n≥ is called the Markov
renewal process of kernel
Q.
Before giving an expression for the marginal distribution of the random vector
(J
n
,T
n
) with values in I
+
× , given that J
0
=i, let us define the marginal
distributions of the (J,T) process ((J
n
,T
n
), n 0≥ ):
0
() ( , ),, , 0, 0
n
ij n n
Qt PJ jT tJ iij In t==≤=∈≥≥. (3.16)
With
ij
A
⎡⎤
=
⎣⎦
A and
ij
B
⎡⎤
=
⎣⎦
B , two mm
×
matrices of integrable functions, we
associate a new matrix •
AB whose general element (
•
AB)
ij
is the function of t
defined by:
1
()() ()().
m
ij kj ik
k
tAtydBy
=
•= −
∫
∑
AB
(3.17)
It can be easily seen that this type of product, called the convolution product for
matrices, is associative but not always commutative.
In the particular case of A=B, we set:
(
)
(2) ( ) ( )
(0) (1)
0
,..., ,
(), .
nn
ij
ij
A
U
δ
⎡
⎤
•= ••= =
⎣
⎦
==
AA A A A A
AAA
(3.18)
If all the functions , , , 1,..., ,
ij ij
ABij m
=
vanish at
∞
−
, we can also use an
integration by parts to express (3.17) as follows:
1
()() ()()
m
ij ik kj
k
tBtydAy
=
•= −
∫
∑
AB
(3.19)
and moreover if A=B, we get:
Markov renewal processes
83
1
()() ()()
m
ij ik kj
k
tAtydAy
=
•= −
∫
∑
AB
. (3.20)
Proposition 3.4 For all 0n ≥ , we have:
()nn
ij ij
QQ= . (3.21)
Moreover, we also have:
()
lim ( )
nn
t
Qt P
→∞
=
. (3.22)
Remark 3.2 It is clear that the above properties proved for SMC are also valid
for ESMC. The only difference is that the T-process can no longer be interpreted
as an extension of a classical renewal process but in fact as a random walk, as the
r.v. T
n
then take their values in and no longer in
+
(see section 14).
4 EXAMPLES
Semi-Markov theory is one of the most productive subjects of stochastic
processes to generate applications in real-life problems, particularly in the
following fields: Economics, Manpower models, Insurance, Finance (more
recently), Reliability, Simulation, Queuing, Branching processes, Medicine
(including survival data), Social Sciences, Language Modelling, Seismic Risk
Analysis, Biology, Computer Science, Chromatography and Fluid mechanics.
Important results in such fields may be found in Janssen (1986) and Janssen and
Limnios (1999).
Let us give three examples in the fields of insurance and reliability.
Example 4.1: The claim process in insurance
Let us consider an insurance company covering m types of risks or having m
different types of customers for the same risk forming the set I={1,…,m}.
For example, in automobile insurance, we can distinguish three types of drivers:
good, average and bad and so I is a space consisting of three states: 1 for good, 2
for average and 3 for bad.
Now, let ( , 1)
n
Xn≥ represent the sequence of successive observed claim
amounts,
(, 1)
n
Yn≥
the sequence of interarrivals between two successive claims
and ( , 1)
n
Jn≥ successive types of observed risks.
In the classical model of risk theory called the Cramer-Lundberg model (1909,
1955), it is supposed that there is only one type of risk and the claim arrival
process is a Poisson process of parameter
λ
; later, Andersen (1967) extends this
model to an arbitrary renewal process and moreover in these two classical
models, the process of claim amounts is a renewal process independent of the
claim arrival process.
84 Chapter 3
The consideration of an SMC for the two-dimensional processes
(( , ), 0)
nn
JX n≥
or/and (( , ), 0)
nn
JY n≥ gives the possibility to introduce a certain dependence
between the successive claim amounts. This model was first developed by
Janssen (1969b, 1970, 1977) along the lines of Miller’s work (1962) and since
then has lead to a lot of extensions, see for example Asmussen (2000).
Example 4.2: Occupational illness insurance
This problem is related to occupational illness insurance with the possibility of
developing partial or permanent disability. In this case the amount of the
incapacitation allowance depends on the degree of disability recognised for the
policyholder by the occupational health doctor, in general on a yearly basis,
because this degree is a function of a professional illness which can become
better or worse.
Considering as in the example Chapter 2, section 9.7, this invalidity degree as a
stochastic process ( , 0)
n
Jn≥ where J
n
represents the value of this degree when
the illness really takes its course, we must then introduce the r.v. X
n
representing
the time between two successive transitions from J
n-1
to J
n
.
In practice, these transitions can be observed with periodic medical inspections.
The assumption that the J-X process is an SMC extends the Markov model of
Chapter 2 and is fully treated in Janssen and Manca (2006).
Example 4.3: Reliability
There are many examples of semi-Markov models in reliability theory, see for
example Osaki (1985) and more recently in Limnios and Oprişan (2001), (2003).
Let us consider a so-called reliability system S that can be at any time t in one of
the m states of I={1,…,m}.
The stochastic process of the successive states of S is represented by
()
,0.
t
SSt=≥
The state space I is partitioned into two sets U and D so that
,,,.IU DU D U D==∅≠∅≠∅∪∩
(4.1)
The interpretation of these two sets is the following : the subset U contains all
“good” states, in which the system is working and the subset D of all “bad “
states in which the system is not working well or has failed.
The indicators used in reliability theory are the following ones:
(i) the reliability function R giving the probability that the system was always
working from time 0 to time t:
[
]
(
)
() , 0, ,
u
R
tPSUu t=∈∀∈ (4.2)
(ii) the pointwise availability function A giving the probability that the system
is working at time t whatever happens on (0,t]:
(
)
() ,
t
At P S U=∈ (4.3)
Markov renewal processes
85
(iii) the maintainability function M giving the probability that the system, being
in D on [0,t), will leave the set D at time t:
[
)
(
)
() , 0, , .
ut
M
tPSDu tSU=∈∈ ∈
(4.4)
5 MARKOV RENEWAL PROCESSES, SEMI-MARKOV
AND ASSOCIATED COUNTING PROCESSES
Let us consider an SMC of kernel Q; we then have the following definitions.
Definition 5.1 The two-dimensional process (J,T)=((J
n
,T
n
),n
0≥
) where T
n
is
given by relation (1.4) is called a Markov renewal sequence or Markov renewal
process.
Çinlar (1969) also gives the term Markov additive process. It is justified by the
fact that, using relation (1.5), we get:
11
11
( , ( , ), 0,..., )
( , ( , ), 0,..., ) Q ( ).
n
nn kk
nn nkk Jjn
PJ jT x J T k n
PJ jX xT JT k n xT
++
++
=≤ =
==≤− ==−
(5.1)
This last equality shows that the (J,T) process is a Markov process with I
+
×
as state space and having the “additive property”:
11nnn
TTX
+
+
=
+
. (5.2)
Let us say that according to the main definitions of Chapter 2,
Definition 2.1,
always in the case of positive (J,X) chains, the random variables ,( 0)
n
Tn≥ are
from now on called Markov renewal times or simply renewal times, the random
variables
,( 1)
n
Xn≥
interarrival or sojourn times and the random variables
,( 0)
n
Jn≥ the state variables.
We will now define the counting processes associated with any Markov renewal
process (in short MRP) as we already did in the special case of renewal theory.
For any fixed time t, the r.v. N(t) represents the total number of jumps or
transitions of the (J,X) process on (0,t], including possible transitions from any
state towards itself (virtual transitions), transitions supposed to be observable.
As in renewal theory, we have:
()
n
N
tt Tt>⇔ ≤. (5.3)
But here, we can be more precise and only count the total number of passages in
a fixed state I always in (0,t] represented by the r.v. N
i
(t).
Clearly, we can write:
1
() (), 0
m
i
i
N
tNtt
=
=
≥
∑
. (5.4)
86 Chapter 3
Definition 5.2 To each Markov renewal process, the following m+1 stochastic
processes are associated respectively with values in
:
(i) the N-process (N(t),t
≥ 0),
(ii) the N
i
-process (N
i
(t),t
0≥
), i=1,…,m,
respectively called the associated total counting process and the associated
partial counting processes with of course:
N(0)=0,N
i
(0)=0,i=1,…,m. (5.5)
It is now easy to introduce the notion of a semi-Markov process by considering at
time t, the state entered at the last transition before or at t, that is J
N(t)
.
Definition 5.3 With each Markov renewal process, we associate the following
stochastic Z-process with values in I:
Z=(Z(t),t
0≥ ), (5.6)
with:
Z(t)=J
N(t)
. (5.7)
This process will be called the associated semi-Markov process or simply the
semi-Markov process (in short SMP) of kernel
Q.
Remarks 5.1
1) As in renewal theory, we will often use counting variables including the
initial renewal, that is:
0
'
'( ) ( ) 1,
() () .
iiiJ
Nt Nt
Nt Nt
δ
=
+
=+
(5.8)
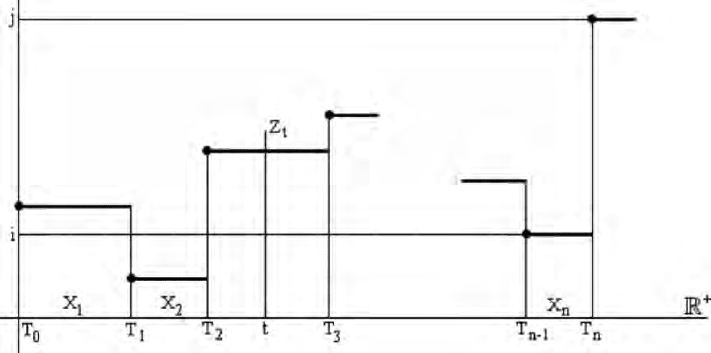
Figure 5.1: a trajectory of an SMP
2)
Figure 5.1 gives a typical trajectory of MRP and SMP.
