Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability
Подождите немного. Документ загружается.

Renewal theory and Markov chains
67
(i) If i is recurrent and if (),jCi
∈
then
1.
ij
f
=
(ii) If i is recurrent and if (),jCi
∉
then
0
ij
f
=
.
Proposition 9.4 Let T be the set of all transient states of I, and let C be a
recurrent class.
For all ,jk C
∈
,
.
ij ik
ff
=
(9.69)
Labeling this common value as
iC
f
, the probabilities
(
)
,
,
iC
f
iT
∈
satisfy the
linear system:
,,
,.
iC ik kC ik
kT kC
f
pf p i T
∈∈
=+ ∈
∑∑
(9.70)
Remark 9.3 Parzen (1962) proved that under the assumption of Proposition 9.4,
the linear system (9.70) has a unique solution. This shows, in particular, that if
there is only one irreducible class
C , then for all iT
∈
:
,
1
iC
f
=
. (9.71)
Definition 9.13 The probability
,iC
f
introduced in Proposition 9.4 is called
absorption probability in class C, starting from state i.
If class
C
is recurrent:
,
1if ,
0 if is recurrent, .
iC
iC
f
iiC
∈
⎧
=
⎨
∉
⎩
(9.72)
9.5 Asymptotic Behaviour
Consider an irreducible aperiodic Markov chain which is positive recurrent.
Suppose that the following limit exists:
lim ( ) ,
jj
n
pn j I
π
→∞
=
∈
(9.73)
starting with
0
J
i=
.
The relation
(1) ()
j
kkj
kI
p
npnp
∈
+=
∑
(9.74)
becomes:
()
(1)
,
n
n
ij kjik
kI
p
pp
+
∈
=
∑
(9.75)
because
()
() .
n
j
ij
p
np= (9.76)
Since the state space I is finite, we obtain from (9.73) and (9.75):
9.4 Computation Of Absorption Probabilities
Proposition 9.3

68 Chapter 2
j
kkj
kI
p
ππ
∈
=
∑
, (9.77)
and from (9.76):
1
i
iI
π
∈
=
∑
. (9.78)
The result:
()
lim
n
ij j
n
p
π
→∞
=
(9.79)
is called an ergodic result, since the value of the limit in (9.79) is independent of
the initial state i .
From result (9.79) and (9.19), we see that for any initial distribution
p:
()
lim ( ) lim ,
n
ijji
nn
j
p
npp
→∞ →∞
=
∑
(9.80)
j
i
j
p
π
=
∑
, (9.81)
so that:
lim ( )
ii
n
pn
π
→∞
=
. (9.82)
This shows that the asymptotic behaviour of a Markov chain is given by the
existence (or non-existence) of the limit of the matrix
n
P
.
A standard result concerning the asymptotic behaviour of
n
P
is given in the next
proposition. The proof can be found in Chung (1960), Parzen (1962) or Feller
(1957).
Proposition 9.5 For any aperiodic Markov chain of transition matrix P and
having a finite number of states, we have:
a) if state j is recurrent (necessarily positive), then
(i)
()
1
() lim ,
n
ij
n
j
j
iCj p
m
→∞
∈⇒ =
(9.83)
(ii) i recurrent and
()
() lim 0,
n
ij
n
Cj p
→∞
∉⇒ =
(9.84)
(iii) i transient
,()
()
lim .
iC j
n
ij
n
jj
f
p
m
→∞
= (9.85)
b) If j is transient, then for all
:iI
∈
()
lim 0.
n
ij
n
p
→∞
=
(9.86)
Remark 9.4
Result (ii) of part a) is trivial since in this case:
()
0
n
ij
p = for all positive n.
From
Proposition 9.5, the following corollaries can be deduced.

Renewal theory and Markov chains
69
Corollary 9.1 (Irreducible case) If the Markov chain of transition matrix P is
irreducible, then for all ,ij I∈ :
()
lim ,
n
ij j
n
p
π
→∞
=
(9.87)
with
1
j
j
j
m
π
=
. (9.88)
It follows that for all
j
:
0
j
π
>
. (9.89)
If we use
Remark 9.3 in the particular case where we have only one recurrent
class and where the states are transient (the so-called uni-reducible case), then we
have the following corollary:
Corollary 9.2 (Uni-reducible case) If the Markov chain of transition matrix P
has one essential class C (necessarily recurrent positive) and T as transient set,
then we have:
(i) for all , :ijC
∈
()
lim ,
n
ij j
n
p
π
→∞
=
(9.90)
with
{
}
,
j
jC
π
∈ being the unique solution of the system:
,
j
iij
iC
p
ππ
∈
=
∑
(9.91)
1
j
jC
π
∈
=
∑
. (9.92)
(ii) For all jT
∈
:
()
lim 0 for all
n
ij
n
p
iI
→∞
=
∈
. (9.93)
(iii) For all :jC
∈
()
lim for all .
n
ij j
n
p
iT
π
→∞
=
∈
(9.94)
Remark 9.5 Relations (9.91) and (9.92) are true because the set C of recurrent
states can be seen as a Markov sub-chain of the initial chain.
If the
transient states belong to the set
{
}
1, ,…
, using a permutation of the set
I , if necessary, then the matrix
P takes the following form:
70 Chapter 2
11 12
22
11
1
1
m
m
+
⎡⎤
⎢⎥
⎢⎥
=
⎢⎥
⎢⎥
+
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎣⎦
PP
P
OP
. (9.95)
This proves that the sub-matrix
22
P
is itself a Markov transition matrix.
Let us now consider a Markov chain of matrix
P. The general case is given by a
partition of I:
1
,
r
ITC C
=
∪∪∪
(9.96)
where T is the set of transient states and
1
,,
r
CC…
the r positive recurrent
classes.
By reorganizing the order of the elements of I , we can always suppose that
{
}
1, ,T
=
…
, (9.97)
{
}
11
1, ,C
ν
=
++…
, (9.98)
{
}
21 12
1, ,C
ν
νν
=++ ++…
, (9.99)
1
1
1, , ,
r
rj
j
Cm
ν
−
=
⎧
⎫
=+ +
⎨
⎬
⎩⎭
∑
… (9.100)
where
j
ν
is the number of elements in
(
)
,1,,
j
C
j
r
=
…
and
1
.
r
j
j
m
ν
=
+
=
∑
(9.101)
This results from the following block partition of matrix
P:
12
11
22
r
rr
νν ν
νν
νν
νν
×× × ×
×
×
×
⎡⎤
⎢⎥
⎢⎥
⎢⎥
=
⎢⎥
⎢⎥
⎢⎥
⎣⎦
PP P P
0P 0 0
00P 0
P
00 0 P
(9.102)
where, for 1, ,jr
=
… :
×
P
is the transition sub-matrix for T ,
j
ν
×
P
is the transition sub-matrix from T to
j
C
,
j
j
ν
ν
×
P is the transition sub-matrix for the class
j
C
.
From
Proposition 9.1, we have the following corollary:
Renewal theory and Markov chains
71
Corollary 9.3 For a general Markov chain of matrix P, given by (9.102), we
have:
(i) For all
iI
∈
and all j T∈ :
()
lim 0.
n
ij
n
p
→∞
=
(9.103)
(ii) For all
(
)
1, , :
j
Cr
ν
ν
∈
= …
()
'
,
if ,
lim 0 if ' ,
if .
j
n
ij
n
iC j
iC
piC
fiT
ν
ν
ν
ν
π
ν
ν
π
→∞
∈
⎧
⎪
=∈≠
⎨
⎪
∈
⎩
(9.104)
Moreover, for all 1, , r
ν
= … :
1.
j
jC
ν
ν
π
∈
=
∑
(9.105)
This last result allows us to calculate the limit values quite simply.
For
()
,,1,,
j
jC r
ν
ν
πν
∈=… , it suffices to solve the linear systems for each
fixed
ν
:
,,
1.
jkkj
kC
i
iC
p
jC
ν
ν
νν
ν
ν
ππ
π
∈
∈
=∈
⎧
⎪
⎨
=
⎪
⎩
∑
∑
(9.106)
Indeed, since each
C
ν
is itself a space set of an irreducible Markov chain of
matrix
ν
ν
×
P
, the above relations are none other than (9.77) and (9.78).
For the absorption probabilities
(
)
,
,,1,,
iC
f
iT r
ν
ν
∈=… , it suffices to solve
the following linear system for each fixed
ν
. Using Proposition 9.4, we have:
,,
,.
iC ik iC ik
kT kC
f
p
f
piT
νν
ν
∈∈
=+ ∈
∑
∑
(9.107)
An algorithm, given in De Dominicis, Manca (1984b) very useful for the
classification of the states of a Markov chain, is fully developed in Janssen and
Manca (2006), section 8.
9.6 Examples
Markov chains appear in many practical problems in such fields as operations
research, business, social sciences, etc.
To give an idea of this potential, we will present some simple examples followed
by a fully developed case study in the domain of social insurance.
(i) A transportation problem. (Anton & Kolman (1978)).
Let us consider a taxicab company of a city
V
, subdivided into three sectors
12
,VV
and
3
V
.
72 Chapter 2
A taxicab picks up a passenger in any sector and drops her or him off in any
sector.
We can view a taxicab as a physical system
S
which can be in one of three
states: the sectors
12
,VV
or
3
V
.
The observation of taxicabs leads to the construction of a Markov chain with
three states.
This Markov chain might have the following matrix
P, for example:
0.5 0.4 0.1
0.3 0.6 0.1 .
0.2 0.1 0.7
⎡
⎤
⎢
⎥
=
⎢
⎥
⎢
⎥
⎣
⎦
P
(9.108)
This matrix is regular, hence irreducible and aperiodic since all its elements are
strictly positive.
(ii) A management problem in an insurance company
A car insurance company classifies its customers in three groups:
0
G : Those having no accidents during the year,
1
G
: Those having one accident during the year,
2
G
: Those having more than one accident during the year.
The statistics department of the company observes that the annual transition
between the three groups can be represented by a Markov chain with state space
{
}
012
,,GGG
and transition matrix P:
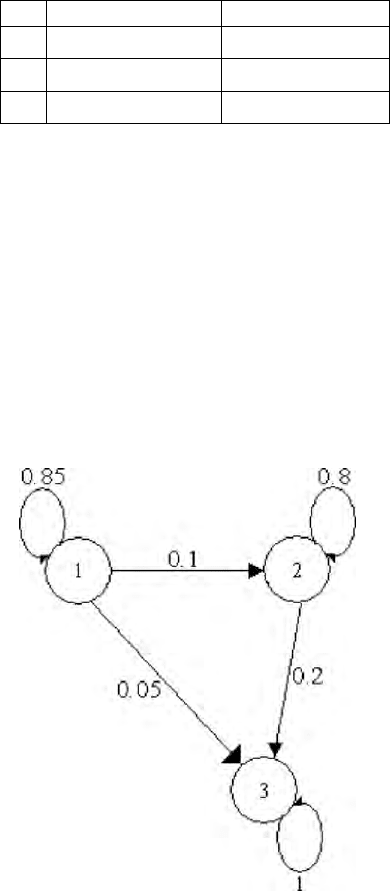
.85 .10 .05
0.80.20
001
⎡
⎤
⎢
⎥
=
⎢
⎥
⎢
⎥
⎣
⎦
P
. (9.109)
We suppose that the company produces 50,000 new contracts per year and wants
to know the distribution of these contracts for the next four years.
After one year, one has, on average:
in group
0
: 50,000 .85 42,500G ×=
,
in group
1
: 50,000 .10 5,000G ×=
,
in group
2
: 50,000 .05 2,500G ×=
.
These results are simply the elements of the first row of
P, multiplied by 50,000.
After two years, multiplying the elements of the first row of
)2(
P
by 50,000, we
get
in group
0
:36,125G
,
in group
1
: 8,250G
,
in group
2
:5,625G
.
A similar computation gives:
Renewal theory and Markov chains
73
After three years After four years
0
G
30,706 26,100
1
G
10,213 11,241
3
G
9,081 12,659
To find the type of the Markov chain with transition matrix (9.109), the simple
graph of possible transitions given in
Figure 9.3 shows that the class
{
}
1, 2
is
transient and class
{
}
3
is absorbing. Thus, using Corollary 9.2 we obtain the
limit matrix
001
001
001
⎡
⎤
⎢
⎥
=
⎢
⎥
⎢
⎥
⎣
⎦
A
. (9.110)
The limit matrix can be interpreted as showing that regardless of the initial
composition of the group; the customers will finish by having at least two
accidents.
Figure 9.3
Remark 9.6
If one wants to know the situation after one or two changes, one can
use relation (1.19) with
1, 2, 3n =
and with p given by:
(.26,.60,.14)
=
p . (9.111)
One obtains the following results:
74 Chapter 2
(1) (1) (1)
123
(2) (2) (2)
123
(3) (3) (3)
123
.257 .597 .146
.255 .594 .151
.254 .590 .156.
ppp
pp p
ppp
===
===
===
These results show that the convergence of
()n
p
to
π
is relatively fast.
9.7 A Case Study In Social Insurance (Janssen (1966))
To compute insurance or pension premiums for professional diseases such as
silicosis, we need to compute the average (mean) degree of disability at pre-
assigned time periods. Let us suppose we retain
m
degrees of disability:
1
,,
m
SS…
, the last being 100% and including the pension paid out at death.
Let us suppose, as Yntema (1962) did, that an insurance policy holder can go
from degree
i
S
to degree
j
S
with a probability
ij
p
. This strong assumption leads
to the construction of a Markov chain model in which the
mm
×
matrix:
[
]
ij
p
=P (9.112)
is the transition matrix related to the degree of disability.
For individuals starting at time 0 with
i
S
as the degree of disability, the mean
degree of disability after the nth transition is:
()
1
() .
m
n
iijj
j
Sn p S
=
=
∑
(9.113)
To study the financial equilibrium of the funds, we must compute the limiting
value of
()
i
Sn
:
lim ( )
ii
n
SSn
→∞
=
, (9.114)
or
()
1
lim .
m
n
iijj
n
j
SpS
→∞
=
=
∑
(9.115)
This value can be found by applying
Corollary 9.3 for 1, ,im
=
… .
Numerical example
Using real-life data for silicosis, Yntema (1962) began with the following
intermediate degrees of disability:

Renewal theory and Markov chains
75
1
2
3
4
5
10%
30%
50%
70%
100%
S
S
S
S
S
=
=
=
=
=
Using real observations recorded in the Netherlands, he considered the following
transition matrix
P:
.90.10000
0.95.050 0
00.90.05.05
000.90.10
0 0 .05 .05 .90
⎡
⎤
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
P
; (9.116)
the transition graph associated with the matrix (9.116) is given in
Figure 9.4:
This immediately shows that:
(i) all states are aperiodic,
(ii) the set
{
}
345
,,SSS
is an essential class (positive recurrent),
(iii) the singleton
{
}
1
and
{
}
2
are two inessential transient classes.
Hence a uni-reducible Markov chain can be associated with matrix
P. We can
thus apply
Corollary 9.2. It follows from relation (9.116) that:
5
3
lim
ijj
n
j
SS
π
→∞
=
=
∑
, (9.117)
where
(
)
345
,,
π
ππ
is the unique solution of the linear system:
33 4 5
534 5
4345
345
.9 0 .05 ,
.05 .9 .05 ,
.05 .05 .9 ,
1.
π
ππ π
π
ππ π
π
πππ
πππ
=⋅ +⋅ + ⋅
=⋅+⋅+⋅
=⋅+⋅+⋅
=++
(9.118)
The solution is:
345
234
,,
999
πππ
=
==
. (9.119)
Therefore:
234
50 70 100 %
999
i
S
⎛⎞
=++
⎜⎟
⎝⎠
(9.120)
or
79%
i
S =
(9.121)
which is the result obtained by Yntema.
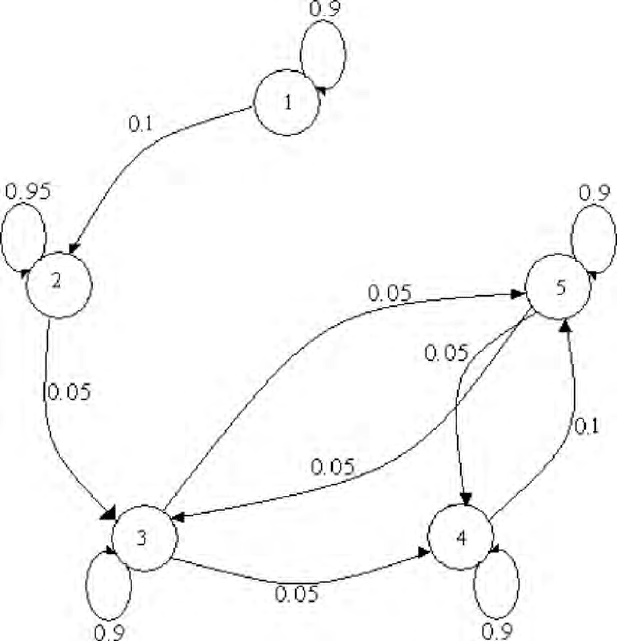
76 Chapter 2
Figure 9.4
The last result proves that the mean degree of disability is, at the limit,
independent of the initial state i.
