Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability
Подождите немного. Документ загружается.


36 Chapter 1
Definition 7.5 The stochastic process X is adapted to the filtration F if, for all t,
the r.v.
X
t
is
t
ℑ
-measurable. This means that, for all ,tT
∈
(
)
{
}
1
:() , .
ttt
XB X B B
ωω
−
=
∈∈ℑ∀∈ℵ
(7.6)
Definition 7.6 Two processes X and Y are indistinguishable if a.s., for all t T∈ ,
.
tt
X
Y
=
(7.7)
This means that
(
)
,1.
tt
XYtT
Ρ
=∀∈=
(7.8)
Definition 7.7 The process X (or Y) is a modification of the process Y (or X) if
a.s., for all t T
∈
,
tt
X
Y
=
a.s. (7.9)
This means that
(
)
., 1.
tt
XY tT
Ρ
=∀∈=
(7.10)
for all tT∈ .
Definition 7.8 For every stochastic process X, the function from T to E,
()
t
tX
ω
(7.11)
defined for each
ω
∈Ω
, is called a trajectory or sample path of the process.
It must be clearly understood that the so-called "modern" study of stochastic
processes is concerned with the study of the properties of these trajectories. For
example, we can affirm that if two processes X and Y are indistinguishable, then
there exists a set N belonging to
ℑ
of probability 0 such that:
:() (), .
tt
N
XYtT
ω
ωω
∀∉ = ∀∈
(7.12)
In other words, for each
ω
element of the set
,
N
Ω
−
the two functions
() and ()
tt
tX tY
ω
ω
are equal. As the basic probability space is complete,
the neglected set N belongs to
t
ℑ
, for all tT
∈
.
Definition 7.9 A real stochastic process X is càdlàg (continu à droite, limite à
gauche) if a.s. the trajectories of X are right continuous and have left limits at
every point t.
Definition 7.10 If X is a real stochastic process and a set
β
Λ
∈
, then the r.v.
defined b:
{
}
() inf 0: ()
t
TtX
ωω
=
>∈Λ
(7.13)
is called the hitting time of
Λ by the process X.
Probability tools 37
It is easily shown that the
properties of stopping and hitting times are (see
Protter (1990)):
(i) If X is càdlàg, adapted and
β
Λ
∈ , then the hitting time related to
Λ
is a
stopping time.
(ii) Let S and T be two stopping times, then the r.v.
{
}
(
)
{
}
(
)
min , , max , , , ( 1)ST ST ST ST ST S
αα
∧
=∨=+> (7.14)
are also stopping times.
Definition 7.11 If T is a stopping time, the
σ
-algebra
T
ℑ
defined by
{
}
{
}
::() ,0
Tt
Tt t
ωω
ℑ=Λ∈ℑΛ ≤ ∈ℑ∀≥∩ (7.15)
is called the stopping time
σ
-algebra.
In fact, the
σ
-algebra
T
ℑ
represents the information of all observable sets up to
the stopping time T. We can also say that
T
ℑ
is the smallest stopping time
containing all the events related to the r.v.
()
()
T
X
ω
ω
for all the adapted càdlàg
processes X or generated by these r.v. We also have for two stopping times S and
T,
(i)
a.s. ,
ST
ST≤⇒ℑ⊂ℑ
(7.16)
(ii) , .
ST ST∧
ℑℑ=ℑ∩ (7.17)
8 MARTINGALES
In this section, we shall briefly present some topics related to the most well-
known category of stochastic processes called martingales. Let X be a real
stochastic process defined on the filtered complete probability space
(
)
(
)
,,, ,
t
PtTΩℑ ℑ ∈ .
Definition 8.1 The process X is called a martingale if:
(i)
(
)
0, ,
t
tEX∀≥ ∃
(8.1)
(ii)
(
)
|,a.s.
ts s
st EXX X<⇒ =
(8.2)
The latter equality is called the martingale property or the martingale equality.
Definition 8.2 The process X is called a super-martingale (resp. sub-martingale)
if:
(i)
(
)
0, ,
t
tEX∀≥ ∃
(8.3)

38 Chapter 1
(ii)
(
)
|(),a.s.
ts s
st EX X<⇒ ℑ ≤≥
(8.4)
The martingale concept is interesting; indeed, as the best estimator at time s (s>t)
for the value of
t
X
, as given by the conditional expectation appearing in relation
(8.2), the martingale equality means that the best predicted value simply is the
observed value of the process at the time of predicting s. The use of martingales
in finance is frequently (see Janssen and Skiadas (1995)) to model the concept of
an efficient financial market.
Definition 8.3 The martingale X is closed if:
()
[
)
()
:
(i) ,
(ii) 0, : ,a.s.
tt
Y
Y
tYX
∃
Ε<∞
∀∈ ∞ Ε ℑ =
(8.5)
It is possible to prove the following result (see for example Protter (1990)).
Proposition 8.1 (i) If X is a supermartingale, then the function
(
)
t
tEX is
right continuous iff there exists a unique modification Y of X such that Y is
càdlàg.
(ii) If X is a martingale then, up to a modification, the function
(
)
t
tEX is
right continuous.
It follows that every martingale such that the function
(
)
t
tEX is right
continuous is càdlàg.
The two most important results about martingales are the martingale
convergence theorem and the optional sampling (or Doob's) theorem. Before
giving these results, we still need a final technical definition.
Definition 8.4
(Meyer (1966)) A family
(
)
,uA
u
ξ
∈ where A is an infinite index
set, is uniformly integrable if:
{}
:()
limsup () () 0
n
n
d
α
α
α
ωξ ω
ξω ω
→∞
≥
Ρ
=
∫
. (8.6)
Proposition 8.2 Let X be a supermartingale in such a way that the function
(
)
t
tEX is right continuous such that:
[
)
(
)
0,
sup
t
t
EX
∈∞
<
∞ ; (8.7)

Probability tools 39
then, there exists a r.v. Y such that
(
)
(i) ,
(ii) lim , a.s.
t
t
EY
YX
→∞
=
(8.8)
Moreover, if X is a martingale closed by the r.v. Z, then the r.v. Y also closes X
and
(
)
,YEZ
∞
=ℑ (8.9)
where
0
.
t
t
σ
∞
≤<∞
⎛⎞
ℑ
=ℑ
⎜⎟
⎝⎠
∪
(8.10)
With the aid of the concept of uniform integrability, we can obtain the following
corollary.
Corollary 8.1 (i) Let X be a right continuous martingale and uniformly
integrable; then the limit
lim
t
t
YX
→∞
=
(8.11)
exists a.s.; moreover
1
YL∈
and the r.v. Y closes the martingale X.
(ii) Let X be a right continuous martingale; then
(, 0)
t
XXt
=
≥
is uniformly
integrable if and only if
lim
t
t
YX
→∞
=
(8.12)
exists a.s.,
1
YL
∈
, and
[
]
()
,0,
t
Xt
∈
∞
is a martingale with, a.s.
.
X
Y
∞
=
(8.13)
Now, an interesting question is: what happens if we observe a martingale X at
two stopping times S,T (S<T, a.s.)? The reply is given by the so-called optional
sampling theorem also called Doob‘s theorem.
Proposition 8.3 (The optional sampling theorem or Doob‘s theorem) Let X be a
right continuous martingale closed by
X
∞
and let S and T be two stopping times
so that a.s. S < T; then the r.v.
1
,
ST
X
XL
∈
and
(
)
, a.s.
STS
XEX=ℑ
(8.14)
This important theorem means that if we restrict the random observation time set
to
S,T{}, then the restriction of the martingale to this set is still a martingale
provided that S and T are two stopping times with of course S<T, a.s. This result
is interesting for the concept of stopped process.

40 Chapter 1
Definition 8.5 Let X be a stochastic process and T a stopping time. The stopped
stochastic process
T
X
is defined by
[
]
(
)
,0,
TT
t
XXt
=
∈∞ (8.15)
where
{}
() (),
inf , .
T
ttT
XX
with t T t T
ωω
∧
=
∧=
(8.16)
From this definition, it follows that if the process X is adapted and càdlàg, then so
is the stopped process
T
X
. This is due to the fact that t
∧
T
is also a stopping
time and moreover,
{} {}
11.
T
tt T
tT tT
XX X
<≥
=+
(8.17)
This leads to the last result we want to mention.
Proposition 8.4 Let X be a right continuous uniformly integrable martingale;
then the stopped process
[
]
(
)
,0,
T
tT
XXt
∧
=
∈∞
has the same properties with
respect to the filtration
[
]
(
)
,0,.
t
tℑ∈ ∞
9 BROWNIAN MOTION
There are a lot of particular stochastic processes and some of them will be
extensively studied in the sequel, such as renewal processes, random walks,
Markov chains, semi-Markov and Markov processes and their main extensions.
However, to finish this introduction to probability theory, we want to introduce
briefly the concept of Brownian motion or Brownian process. We will work on a
basic complete filtered probability space satisfying the usual assumptions and
denoted
[
)
()
(
)
,,, , 0, .
t
PtΩℑ ℑ ∈ ∞
Definition 9.1 The real stochastic process
[
)
(
)
,0,
t
BBt
=
∈∞ will be called a
Brownian motion or Brownian or Wiener process with trend
μ
and variance
2
σ
provided that:
(i) B is adapted to the basic filtration,
(ii) B has independent increments,
i. e. that:
(
)
(
)
, (0 ) : ,
,
ts S ts
s
t st PBB A PBB A
Borel sets B
∀≤< −∈ℑ=−∈
∀
(9.1)
(iii) B has stationary increments, i.e.:
Probability tools 41
2
, (0 ): ((-), (-)),
ts
s
t s t B B has a normal distribution N t s t s
μσ
∀≤< − (9.2)
(iv)
(
)
0
1, ( ).PB x x== ∈ (9.3)
If moreover, we have
2
0, 1, 0,x
μσ
=
==
(9.4)
then the Brownian motion is called standard.
Let us now give the most important properties of the standard Brownian motion.
Property 9.1 If B is a Brownian motion, then there exists a modification of B, the
process B*, such that B* has, a.s., continuous trajectories.
Property 9.2 If B is a standard Brownian motion, then B is a martingale.
Property 9.3 If B is a standard Brownian motion, then the process Q where
[
)
(
)
2
,0,
t
QBtt
=
−∈∞
(9.5)
is a martingale.
Remark 9.1 It can also be proved that both Properties 9.2 and 9.3 characterise
a standard Brownian motion.
Property 9.4 If B is a standard Brownian motion, then for almost all
ω
, the
trajectory
()
t
B
ω
ω
is not of bounded variation on every closed interval
[]
,.ab
This explains why it is necessary for models in finance and in insurance to define
a new type of integral, called the Itô or stochastic integral, if we want to
intregrate with respect to B (see for example Protter (1990)). This will be done in
Chapter 5, section 4.2.
Chapter 2
RENEWAL THEORY AND MARKOV CHAINS
In this chapter, the reader will find a summary of the basic results on renewal
theory and Markov processes useful for understanding of the following chapters.
A more detailed version with proofs can be found in Janssen and Manca
(2006)
(Chapters 2 and 3)
1 PURPOSE OF RENEWAL THEORY
Let us consider the following reliability problem: at time 0, the given system
starts with a new component which fails at random time
1
T . At this time, a new
component immediately enters the system to replace the first one and fails at time
c. There is another immediate replacement by a new component inserted in the
system, still of the same type, and so on.
We will note
(
)
,0
n
Tn≥ the successive replacement times, setting, of course:
0
0T
=
. (1.1)
The
lifetimes of the successive components entering the system are given by
1
,1
nnn
XTT n
−
=
−≥
. (1.2)
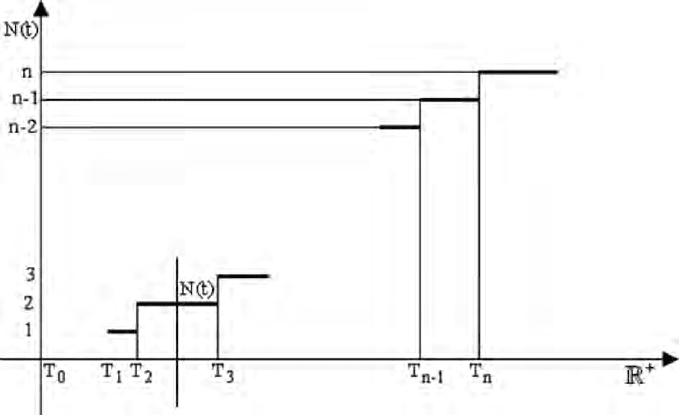
Figure 1.1:trajectory of ()
N
t
44 Chapter 2
From an operational point of view, an important characteristic of the considered
system at time t is the total number of replacements occurring on the
interval
[]
0,t . Let us remark that, for the moment, we do not take into account
the initial component. If ( )
N
t represents the random variable we have just
defined, we have, for
1n ≥ :
() 1
n
N
tn Tt>−⇔ ≤. (1.3)
It is possible to represent a realization of the stochastic process
(
)
(), 0Nt t≥
,
as shown in
Figure 1.1.
The first moment of ( )
N
t will give the mean number of replacements on (0, ]t .
In particular, if at time 0 the manager must be able to have an inventory large
enough to perform all replacements, the level of the inventory will be, on
average, the expectation
(
)
(
)
E
Nt . Of course, the manager must add buffer
stock to prevent random evolution. This problem will be solved in section 7. The
area of probability studying such processes is called Renewal Theory. It is, at
least for applied probability, one of the most important topics encountered in real
life problems.
2 MAIN DEFINITIONS
Let
(
)
,1
n
Xn≥ be a sequence of non-negative, independent and identically
distributed random variables defined on the probability space
(
)
,,P
Ω
ℑ .
Definition 2.1 The random sequence
(
)
,0
n
Tn≥ , where:
0
0T
=
a.s., (2.1)
1
,1,
nn
TX X n=++ ≥ (2.2)
is called a renewal sequence or renewal process.
The r.v. ,0
n
Tn≥ are called renewal times and the r.v. ,1
n
Xn≥ are called
interarrival times.
Example 2.1
1) In the first section, we give an example in reliability theory.
2) Another important example is queueing theory. Let us consider a queueing
system composed of a server, a process of customer arrivals, a process of service
times and a discipline rule of the type “first in, first out” (FIFO), which means
the first customer present in the system is the first served.
In many models of queueing theory, the arrival process is assumed to be a
renewal process.

Renewal theory and Markov chains
45
In this case, the r.v.
n
T is the arrival time of the nth customer, assuming that a
customer number 0 is immediately served at time 0, and the r.v.
n
X
represents
the interarrival time between the ( 1n
−
)th and the nth customer.
3) An arrival process is also considered in risk theory. Let us consider an
insurance company starting at time 0 with a capital amount u
(
)
0u ≥
called the
initial reserve. The customers pay premiums, and the insurance company has to
pay for the accidents claimed by the customers. In this case, the r.v.
n
T represents
the arrival of the nth claim, assuming that the company just starts at the arrival of
a claim called claim 0, and the r.v.
n
X
is the interarrival time between the
(1n − )th and the nth claims
(
)
1n ≥ .
4) In counter theory, we consider particles arriving at times , 0
n
Tn≥ with
0
0T =
so that here too, the r.v.
n
X
are interpreted in terms of interarrival time
between two successive particles.
Definition 2.2 With each renewal sequence, we can associate the following
stochastic process, continuous in time, with values in :
(
)
(), 0Nt t≥
, (2.3)
where
0
() 1 ,
n
Nt n T t n>−⇔ ≤ ∈ .
This process is called the associated counting process or the renewal counting
process.
()
N
t represents the total number of “renewals” on (0, ]t.
Definition 2.3 The renewal function is defined as
() ( ())Ht ENt
=
(2.4)
provided the expectation is finite.
3 CLASSIFICATION OF RENEWAL PROCESSES
Let us suppose that the random variables are defined on with distribution
function F such that, to avoid trivialities:
(0) 1F
<
. (3.1)
If
()1F
+
∞= , (3.2)
we have the usual case of real random variables.
From relation (2.2), we get
(
)
()
P() 1 (), 1
n
Nt n F t n>− = ≥
, (3.3)
()n
F
being the n-fold convolution product of F with itself.
Since, for 1n
≥ :
46 Chapter 2
(
)
(
)
(
)
() () 1 ()PNt n PNt n PNt n== >−− > , (3.4)
using relation (3.3), we obtain:
(
)
() ( 1)
() () (), 1
nn
PNt n F t F t n
+
== − ≥
. (3.5)
(0)
F
is defined as being the Heaviside distribution with a unit mass at the origin,
i.e.,
(0)
0
F
U= ; (3.6)
the relation (3.5) is still valid for 0
n
=
, since
(
)
P()01 ().
N
tFt
=
=− (3.7)
Using Stein’s lemma (1946), the following very important result can be proved:
Proposition 3.1 If (0) 1F < , then, for all ,()tNt has moments of any order.
In particular, this proposition implies that the renewal function is finite for all
finite
t. Consequently, we can write successively:
()
[]
() ( 1)
1
(2) (2) (3)
(2) (3)
() () ()
() () 2 () 2 ()
() () () ,
nn
n
ENt nF t F t
FtFt Ft Ft
Ft F t F t
∞
+
=
=−
=− + − +
=+ + +
∑
(3.8)
so that using relation (2.4):
()
1
() ().
n
n
H
tFt
∞
=
=
∑
(3.9)
In several cases, it is useful to consider the initial renewal and to define at time t
the random variable '( )
N
t as being the total number of renewals on
[]
0,t .
Clearly, we have, for all
0t ≥
:
'( ) ( ) 1,Nt Nt
=
+ (3.10)
and consequently:
(
)
'( ) ( ) 1ENt Ht
=
+ . (3.11)
Setting
(
)
() '()
R
tENt
=
, (3.12)
we get from relations (3.11), (3.9) and (3.6):
()
0
() ().
n
n
R
tFt
∞
=
=
∑
(3.13)
Of course, we have
0
() () ()
R
tUtHt
=
+ . (3.14)
The classification of a renewal process is based on three concepts: recurrence,
transience and periodicity.
