Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability

16 Chapter 1

0

(),0,...,.

jnj ini

n

PY ud S pq i n

i

−−

⎛⎞

== =

⎜⎟

⎝⎠

(5.9)

This distribution is currently used in the financial model of Cox, Ross and

Rubinstein (1979) developed in Chapter 5.

5.2 The Poisson Distribution

If X is a r.v. with values in  so that the probability distribution is given by

() ,0,1,...

!

i

PX i e i

i

λ

−

== = (5.10)

where

λ

is a strictly positive constant, X is called a Poisson variable of

parameter

λ

. This is one of the most important distributions for all applications.

For example if we consider an insurance company looking at the total number of

claims in one year, this variable often may be considered as a Poisson variable.

Basic parameters of this Poisson distribution are given here:

(1) (1)

() , var() ,

() , () .

it t

ee

XX

EX X

te gte

λλ

λ

ϕ

−−

=

==

(5.11)

A remarkable result is that the Poisson distribution is the limit of a binomial

distribution of parameters (

n,p) if n tends to

+

∞ and p to 0 so that np converges

to

λ

.

The Poisson distribution is often used for the occurrence of rare events. For

example if an insurance company wants to hedge the hurricane risk in the States

and if we know that the mean number of hurricanes per year is 3, the adjustment

of the r.v.

X defined as the number of hurricanes per year with a Poisson

distribution of parameter

3

λ

=

gives the following results:

P(X=0)=0.0498, P(X=1)=0.1494, P(X=2)=0.2240, P(X=3)=0.2240,

P

(X=4)=0.1680, P(X=5)=0.1008,P(X=6)=0.0504, P(X>6)=0.0336.

So the probability that the company has to hedge two or three hurricanes per year

is 0.4480.

5.3 The Normal (or Laplace-Gauss) Distribution

The real r.v. X has a normal (or Laplace-Gauss) distribution of parameters

22

(, ), , 0

μσ μ σ

∈> , if its density function is given by

2

()

2

1

() ,

2

x

X

fx e x

μ

σ

π

−

=

∈ . (5.12)

From now on, we will use the notation

2

(, )XN

μ

σ

≺ . The main parameters of

this distribution are

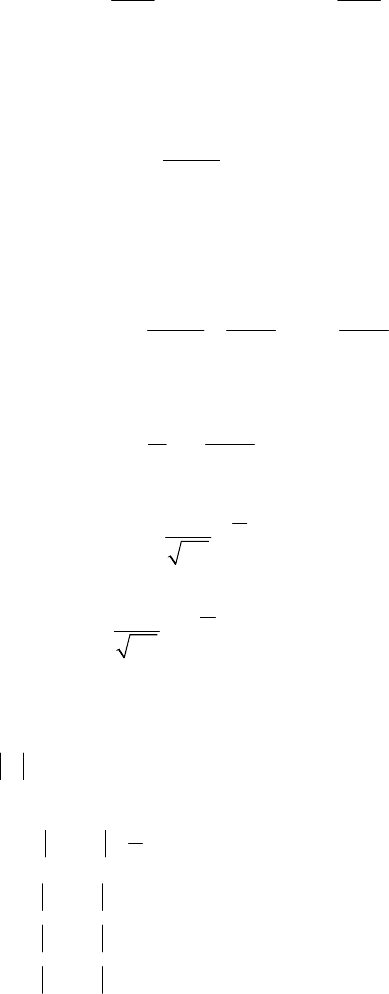
Probability tools 17

2

22 22

() , var() ,

() exp , () exp .

22

XX

EX X

tt

tit gt t

μσ

σσ

ϕμ μ

==

⎛⎞ ⎛⎞

=− =+

⎜⎟ ⎜⎟

⎝⎠ ⎝⎠

(5.13)

If

2

0, 1

μσ

==, the distribution of X is called a reduced or standard normal

distribution. In fact, if X has a normal distribution

22

(, ), , 0R

μσ μ σ

∈

> , then the

so-called reduced r.v. Y defined by

X

Y

μ

σ

−

= (5.14)

has a standard normal distribution, thus from (5.13) with mean 0 and variance 1.

Let Φ be the distribution function of the standard normal distribution; it is

possible to express the distribution function of any normal r.v. X of parameters

22

(, ), , 0

μσ μ σ

∈> as follows:

() ( )

X

Xx x

Fx PX x P

μ

μμ

σσ σ

−− −

⎛⎞⎛⎞

=≤= ≤ =Φ

⎜⎟⎜⎟

⎝⎠⎝⎠

. (5.15)

Also from the numerical point of view, it suffices to know numerical values for

the standard distribution. From relation (5.15), we also deduce that

1

() '

X

x

fx

μ

σσ

−

⎛⎞

=Φ

⎜⎟

⎝⎠

, (5.16)

where of course from (5.12)

2

1

'( )

2

x

e

π

−

Φ= . (5.17)

From the definition of Φ , we have

2

1

() ,

2

x

y

xedyx

π

−

−∞

Φ= ∈

∫

 (5.18)

and so

()1 (), 0xxx

Φ

−=−Φ >, (5.19)

and consequently, for X normally distributed with parameters (0,1), we get

(

)

() ( ) 2 () 1, 0PXxxxxx≤=Φ−Φ−=Φ− >. (5.20)

In particular, let us mention the following numerical results:

()

2

0.4972( 50%),

3

0.6826( 68%),

2 0.9544( 95%),

3 0.9974( 99%).

PX m

σ

⎛⎞

−≤ = ≈

⎜⎟

⎝⎠

−≤ = ≈

(5.21)

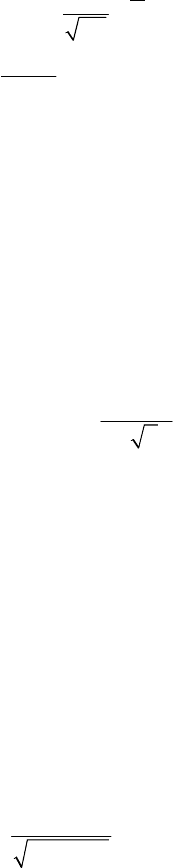
18 Chapter 1

Remark 5.1: Numerical computation of the d.f.

Φ

For applications in finance,

for example the Black Scholes (1973) model for option pricing (see Chapter 5),

we will need the following numerical approximation method for computing Φ

with seven exact decimals instead of the four given by the standard statistical

tables:

2

5

2

15

1

23

45

1) 0 :

1

() 1 ( ),

2

1

,

1

0,2316419, 0,319381530,

0,356563782, 1,781477937,

1,821255978, 1,330274429,

2) 0 :

() 1 ( ).

x

xebcbc

c

px

pb

bb

x

xx

π

−

>

Φ≈− ++

=

+

==

=− =

<

Φ=−Φ−



(5.22)

The normal distribution is one of the most often used distributions, by virtue of

the Central Limit Theorem which says that if

(, 1)

n

Xn≥

is a sequence of

independent identically distributed (in short i.i.d.) r.v. with mean m and variance

2

,

σ

then the sequence of r.v. defined by

n

Snm

n

σ

−

(5.23)

with

1

,0

nn

SX Xn

=

++ > (5.24)

converges in law to a standard normal distribution. This means that the sequence

of the distribution functions of the variables defined by (5.21) converges to Φ .

This theorem was used by the Nobel Prize winner H. Markowitz (1959) to justify

that the return of a diversified portfolio of assets has a normal distribution. As a

particular case of the Central Limit Theorem, let us mention de Moivre’s theorem

starting with

1, with prob. ,

0, with prob. 1 ,

n

p

X

p

⎧

=

⎨

−

⎩

(5.25)

so that, for each n, the r.v. defined by relation (5.22) has a binomial distribution

with parameters (n,p). By applying now the Central Limit Theorem, we get the

following result:

(0,1),

(1 )

law

n

Snp

N

np p

→+∞

−

⎯⎯⎯→

−

(5.26)

called de Moivre‘s result.

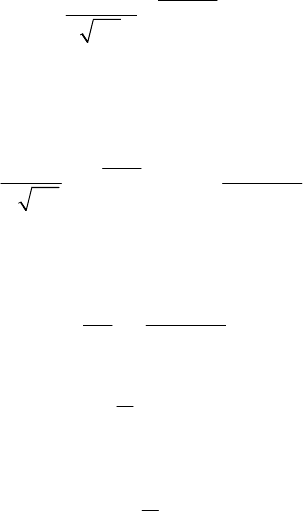
Probability tools 19

5.4 The Log-Normal Distribution

If the normal distribution is the most frequently used, it is nevertheless true that it

could not be used for example to model the time evolution of a financial asset

like a share or a bond, as the minimal value of these assets is 0 and so the support

of their d.f. is the real half-line

[

)

0,

+

∞ . One possible solution is to consider the

truncated normal distribution to be defined by setting all the probability mass of

the normal distribution on the negative real half-line on the positive side, but then

all the interesting properties of the normal distribution are lost.

Also, in order to have a better approach to some financial market data, we have

to introduce the log-normal distribution. The real non-negative random variable

X has a lognormal distribution of parameters ,

μ

σ

−

and we will write

(,)XLN

μ

σ

≺ − if the r.v. logX has a normal distribution with parameters

2

,

μ

σ

.

Consequently, the density function of X is given by

()

2

log

2

0, 0,

1

,0.

2

x

X

x

fx

ex

x

μ

σ

πσ

−

≤

⎧

⎪

=

⎨

≥

⎪

⎩

(5.27)

Indeed, we can write

(

)

(

)

log log ,PX x P X x≤= ≤ (5.28)

and so

()

2

log

2

1log

,

2

t

x

X

x

Fx e dt

μ

σ

μ

σ

σπ

−

−∞

⎛⎞

−

⎛⎞

==Φ

⎜⎟

⎝⎠

∫

(5.29)

and after the change of variable t=logx, we get the relation (5.27). Let us remark

that the relation (5.29) is the most useful one for the computation of the d.f. of X

with the help of the normal d.f. For the density function, we can also write

1log

()

X

x

fx

x

μ

σσ

−

⎛⎞

=Φ

⎜⎟

⎝⎠

. (5.30)

The basic parameters of this distribution are given by

()

2

22

2

() ,

var( ) 1 ,

.

r

EX e

Xe e

EX e

σ

μ

μσ σ

σ

μ

+

⎛⎞

+

⎜⎟

⎝⎠

=

−

=

(5.31)

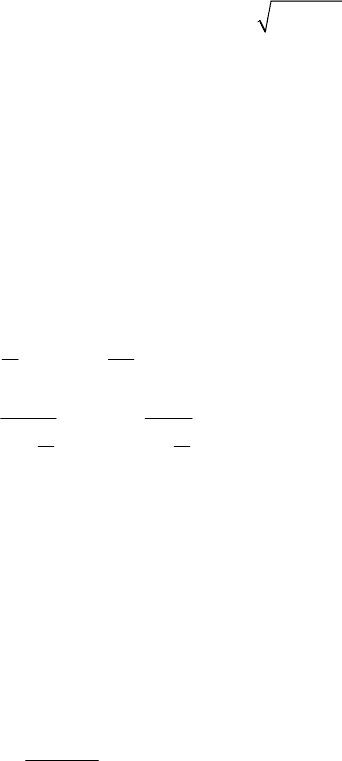
20 Chapter 1

Let us say that the log-normal distribution has no generating function and that the

characteristic function has no explicit form. When

0.3

σ

<

, some authors

recommend a normal approximation with parameters

2

(, )

μ

σ

.

The normal distribution is stable under the addition of independent random

variables; this property means that the sum of n independent normal r.v. is still

normal. That is no longer the case with the log-normal distribution which is

stable under multiplication, which means that for two independent log-normal

r.v. X

1

,X

2

, we have

(

)

22

12 121 2

(,), 1,2 ,

iii

XLN i XX LN

μ

σμμσσ

=⇒× + +≺≺. (5.32)

5.5 The Negative Exponential Distribution

The non-negative r.v. X has a negative exponential distribution (or simply

exponential distribution) of parameter

λ

if its density function is given by

() , 0

x

X

fx e x

λ

−

=

≥ , (5.33)

where

λ

is a strictly positive real number. By integration, we get the explicit

form of the exponential distribution function

() 1 , 0

x

X

Fx e x

λ

−

=

−≥. (5.34)

Of course, F

X

is null for negative values of x. The basic parameters are

2

11

() ,var ,

11

() , () , .

11

XX

EX X

tgtt

tt

i

λλ

ϕ

λ

λλ

==

=

=<

−−

(5.35)

In fact, this distribution is the first to be used in reliability theory.

5.6 The Multidimensional Normal Distribution

Let us consider an n-dimensional real r.v. X represented as a column vector of its

n components

1

( ,..., )'.

n

XX X= Its d.f. is given by

111

( ,..., ) ( ,..., )

X

nnn

F

xxPXxXx

=

≤≤

. (5.36)

If the density function of X exists, the relations between the d.f. and the density

function are

1

11

1

111

( ,..., ) ( ,..., ),

...

( ,..., ) ... ( ,..., ) ,..., .

n

X

Xn n

n

x

X

nXnn

F

fx x x x

xx

F

xx f d d

ξ

ξξ ξ

−∞ −∞

∂

=

∂∂

=

∫∫

(5.37)

Probability tools 21

For the principal parameters we will use the following notation:

22

( ) , 1,..., ,

(( )( )) , , 1,..., ,

(( )) , 1,..., ,

(( )( ))

, , 1,..., .

(( ) ) (( ) )

kk

kkll kl

kk k

kkll kl

kl

kk kk

EX k n

EX X kl n

EX k n

EX X

kl n

EX EX

μ

μμσ

μσ

μμ σ

ρ

σσ

μμ

==

−−==

−==

⎛⎞

−−

===

⎜⎟

−−

⎝⎠

(5.38)

The parameters

kl

σ

are called the covariances between the r.v. X

k

and X

l

and the

parameters

kl

ρ

, the correlation coefficients between the r.v. X

k

and X

l

. It is well

known that the correlation coefficient

kl

ρ

measures a certain linear dependence

between the two r.v. X

k

and X

l

. More precisely, if it is equal to 0, there is no such

dependence and the two variables are called uncorrelated; for the values +1 and

–1 this dependence is certain.

With matrix notation, the

nn× matrix

X

ij

σ

⎡

⎤

=

⎣

⎦

Σ (5.39)

is called the variance –covariance matrix of X. The characteristic function of X

is defined as:

(

)

(

)

(

)

11 1

(.. )

'

1

( ,..., )

nn

itX tX

iX

Xn

ttEe Ee

ϕ

++

==

t

. (5.40)

Let ,

μΣ be respectively an n-dimensional real vector and an

nn×

positive

definite matrix. The n-dimensional real r.v. X has a non-degenerated n-

dimensional normal distribution with parameters ,

μΣ if its density function is

given by

1

()'()

2

1

() , .

(2 ) det

n

X

n

fe

π

−

−− −

=∈

x μΣ x μ

xx

Σ

 (5.41)

Then, it can be shown by integration that parameters ,

μΣ are indeed respectively

the mean vector and the variance-covariance matrix of X. As usual, we will use

the notation: ( , )

n

XNμΣ≺ .

The characteristic function of X is given by

1

''

2

()

i

X

e

ϕ

−

=

μ ttΣt

t . (5.42)

The main fundamental properties of the n-dimensional normal distribution are:

-every subset of k r.v. of the set {X

1

,…,X

n

} has also a k-dimensional distribution

which is also normal;

-the multi-dimensional normal distribution is stable under linear transformations

of X;

22 Chapter 1

-the multi-dimensional normal distribution is stable for addition of random

variables, which means that if

( , ), 1,...,

knkk

X

Nkm

=

μΣ≺

and if these m random

vectors are independent, then

111

(, )

mn m m

XXN++ ++ ++μμΣΣ≺   . (5.43)

Particular case: the two-dimensional normal distribution

In this case, we have

2

112

12

2

12

21 2

2

112

12

2

12 2

(, )', , ,

1

,det 1 .

1

σσ

σ

μμ ρ

σσ

ρ

σςσ

σ

σρ

ρ

ςσ σ

−

⎡⎤

== =

⎢⎥

⎣⎦

⎡⎤

−

⎢⎥

==−

⎢⎥

−

⎢⎥

⎣⎦

μΣ

ΣΣ

(5.44)

From the first main fundamental properties of the

n-dimensional normal

distribution given above, we have

2

1

(, ), 1,2

kkk

XN k

μσ

=≺ . (5.45)

For the special degenerated case of

1

ρ

=

, it can be proved that

22 11

21

22 11

21

1 : ,

XX

μ

ρ

σσ

μ

ρ

σσ

−

==

−−

=− =−

(5.46)

relations meaning that in this case, all the probability mass in the plan lies on a

straight line so the two random variables X

1

,X

2

are perfectly dependent with

probability 1.

To finish this section, let us recall the well-known property saying that two

independent r.v. are uncorrelated but the converse is not true except for the

normal distribution.

6 CONDITIONING (FROM INDEPENDENCE TO

DEPENDENCE)

6.1 Conditioning: Introductory Case

Let us begin to recall briefly the concept of conditional probability. Let ( , , )PΩℑ

be a probability space and let A, B be elements of

ℑ

and look at the number of

occurrences of the event A whenever B has already been observed in a sequence

of n trials of our experiment. We shall call this number

(

)

nAB

.

In terms of frequency of events defined by relation (2.5), we have

Probability tools 23

()

nA B

nAB

nB

=

∩

, (6.1)

provided that n(B) is different from 0. Dividing by n the two members of relation

(6.1), we get

()

nA B

nAB

n

nB

n

=

∩

. (6.2)

In terms of frequencies, we get

()

f

AB

fAB

fB

=

∩

. (6.3)

From the experimental interpretation of the concept of probability of an event

seen in section 2, we can now define the conditional probability of A given B as

()

,() 0

()

PA B

PAB PB

PB

=

>

∩

. (6.4)

If the events A and B are independent, from relation (4.39), we get

(

)

()PAB PA= , (6.5)

a relation meaning that, in case of independence, the conditional probability of

set A does not depend on the given set B. As the independence of sets A and B is

equivalent to the independence of sets A and B

c

, we also have:

(

)

()

c

PAB PA=

. (6.6)

The notion of conditional probability is very useful for computing probabilities

of a product of dependent events A and B not satisfying relation (4.39). Indeed

from relations (6.4) and (6.6), we can write

(

)

(

)

( ) () ()PA B PAP AB PBP BA==∩ . (6.7)

More generally, for n events A

1

,…,A

n

, we get the so-called “theorem of

compound probability”:

()()

121 12 1

1

( ) ...

n

knn

k

PAPAPAAPAAA A

−

=

⎛⎞

=

⎜⎟

⎝⎠

∩∩

∩

, (6.8)

a relation expanding relation (6.7).

1

( )... ( )

n

kn

k

P A PA PA

=

⎛⎞

=

⎜⎟

⎝⎠

∩

(6.9)

is true in the case of independence of the n considered events. If the event B is

fixed and of strictly positive probability, relation (6.4) gives the way to define a

new probability measure on ( , )

Ω

ℑ denoted P

B

as follows:

()

() ,

()

B

PA B

PA A

PB

=

∀∈ℑ

∩

. (6.10)

24 Chapter 1

P

B

is in fact a probability measure as it is easy to verify that it satisfies conditions

(2.10) and (2.11) and so P

B

is called the conditional probability measure given B.

The integral with respect to this measure is called the conditional expectation E

B

relative to P

B

. From relation (6.10) and since P

B

(B)=1, we thus obtain for any

integrable r.v. Y:

1

() () ()

()

BB

E

YYdP YdP

PB

ωω

ΩΩ

==

∫∫

. (6.11)

For our next step, we shall now consider a countable event partition ( , 1

n

Bn≥ ) of

the sample space Ω . That is,

1

,, ,:

ni j

n

B

BB ijij

∞

=

Ω= =∅ ∀ ≠∩

∪

. (6.12)

Then, for every event A, we have

1

() ( )

n

PA PB A

≥

=

∑

∩

(6.13)

and by relation (6.10),

(

)

1

() ( )

nn

n

PA PB P AB

≥

=

∑

. (6.14)

Now, for any integrable r.v. Y, we can write

1

() ()

n

B

E

YYdP

ω

≥

=

∑

∫

(6.15)

and from relation (6.11),

1

() ( ) ()

n

nB

n

E

YPBEY

≥

=

∑

. (6.16)

As the partition , 1

n

Bn≥ generates a sub-

σ

-algebra of

ℑ

denoted

1

ℑ

obtained as

the minimal sub-

σ

-algebra containing all the events of the given partition, we

can now define

1

()

E

Y

ℑ

, called the conditional expectation of Y given

1

ℑ

, as

follows:

1

()() ()1()

nn

BB

n

EY EY

ω

ℑ

≥

=

∑

. (6.17)

It is very important to understand that this conditional expectation is a function of

ω

and so a new random variable. So, the random variable

1

()

E

Y

ℑ

assumes on

each set B the value of ( )

n

B

E

Y that is constant and defined by relation (6.11) with

B=B

n

.

Now, let us compute the expectation of this new random variable

1

()

E

Y

ℑ

; from

relation (6.17), we can deduce that

Probability tools 25

()

1

()() ()1()

( )1 ( )

( ) 1 ( )

( ) ( )

nn

n

BB

n

BB

n

BB

n

Bn

n

EE Y E E Y

EE Y

EYE

EYPB

ω

ℑ

≥

⎛⎞

=

⎜⎟

⎝⎠

=

∑

(6.18)

and finally from relation (6.16), we get

1

( ( )( )) ( ).

E

EY EY

ω

ℑ

=

(6.19)

Furthermore, since for any set B belonging to

1

ℑ

, B is the union of a certain

number of events B

n

, finite or at the most denumerable, we obtain by integrating

both members of relation (6.17):

1

()() ()1()

( ) 1 ( )

( ) ( ).

nn

n

BB

n

BB

n

B

Bn

n

E

YdP EY dP

E

YdP

E

YPB B

ωω

ω

ℑ

≥

=

∑

∫∫

∑

∫

∑

∩

(6.20)

Using now relation (6.11), we get:

1

()() () ( )

()

( )

( ) .

n

BBB

n

BB

B

E

YdP YdPPBB

PB B

YdP

ωω

ω

ℑ

≥

∩

≥

∩

⎛⎞

=

⎜⎟

⎝⎠

=

∑

∫∫

∑

∫

∩

(6.21)

In conclusion, we get

1

()() () , .

BB

EY dP Y dPB

ωω

ℑ

=

∈ℑ

∫∫

(6.22)

Of course, for

B

=Ω, this last relation is identical to (6.19).

We shall focus our attention on the meaning of result (6.22) which equates two

integrals on every set B belonging to

1

ℑ

but presenting an essential difference: in

the left member, the integrand

1

()

E

Y

ℑ

is

1

ℑ

-measurable but in the right member,

the integrand Y is ℑ-measurable and so not necessarily

1

ℑ

-measurable since

1

.ℑ⊂ℑ Furthermore, the function

1

()

E

Y

ℑ

is a.s. unique; indeed, let us suppose

Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability

Подождите немного. Документ загружается.