Jacques J., Raimondo M. Semi-markov risk models for finance, insurance and reliability

Подождите немного. Документ загружается.

Discrete time SMP and numerical solution 147

4.2.2 Non-Homogeneous Case

As above in the homogoneous case, we consider that a taxicab driver will work

for eight hours with time intervals of 15 minutes and so we will consider the

transient case within 32 time periods for which

(,)

represents the probability

that a driver being in state i at time s will be in state j at time t.

Though this example is one of the simplest that can be done, it will clearly

confirm that non-homogeneity, as already shown, gives some intrinsic

supplementary difficulties.

Also, we will try to show all the steps that are necessary to understand the

development of a DTNHSMP.

This time, the input is:

m = 3,

T = 32,

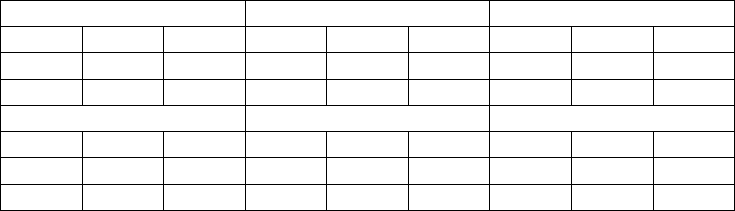
and the non-homogeneous Markov chain, reported in the following table.

P(0) P(5) P(10)

0.3 0.4 0.3 0.39 0.35 0.26 0.49 0.3 0.21

0.4 0.2 0.4 0.35 0.32 0.33 0.3 0.42 0.28

0.32 0.38 0.3 0.28 0.33 0.39 0.23 0.28 0.49

P(20) P(25) P(29)

0.54 0.35 0.11 0.5 0.4 0.1 0.5 0.4 0.1

0.3 0.62 0.08 0.3 0.6 0.1 0.3 0.6 0.1

0.23 0.18 0.59 0.24 0.13 0.63 0.2 0.1 0.7

Other input should be the matrix

[

]

(,)

st=F , the discrete time increasing

probability distribution of the waiting time in each state i, given that the arrival

time in the state i was at time s and that the next state to be successively occupied

is j.

From the data, we can construct these distribution functions, as in the

homogeneous cases.

To compute for each s, i and j the related d.f.,

(,), (, 1), (, 2), , (,32), 32,

ij ij ij ij

FssFss Fss Fs s

+≤… (4.11)

we first introduce the following quantities:

() ( (, 1), (, 2), , (,32), (,33))

ij ij ij ij ij

svss vss vs vs=+ +v … . (4.12)

(, 1)

vss+

gives the number of all the runs for which the taxi driver arrived at

time s in the state i and finished the new course in the state j in a time less than or

equal to 15 minutes (including the waiting time before beginning the new

course).

148 Chapter 4

Similarly ( , 2)

vss+ gives the number of all the runs for which the taxi driver

arrived at time s in the state i and finished the new run in the state j in a time

more than 15 minutes and less than or equal to 30 minutes and so on.

Finally, ( ,32)

vs gives the number of all the courses from i and j that began at

the arrival time s and finished after 7.45 hours but within the eight hours of the

turn and ( ,33)

vs the number of taxi drivers who arrived at time s in i and who

will finish the next course in j, but after the eight hours.

It is important to remark that in the semi-Markov environment the stopping time

of the taxidriver before the beginning of another run is included in the duration of

the course.

From the vector ( )

v we can construct the vector ( )

w :

(,) (, ) 1, ,33

ij ij

wst vss h t s

=+=+

∑

… . (4.13)

We finally obtain the elements of the matrix

F given by:

(,)

(,) 0, (,) , 1, ,32.

(,33)

ij ij

wst

Fss Fst t s

== =+

… (4.14)

In place of real data not available here, we construct the

F matrix by means of

pseudorandom generator numbers as for the homogoneous case given above.

We can then multiply matrices

F and P and obtain the matrix Q with the relation

(,) () (,)

tsst

⋅QPF. (4.15)

The next matrix to be computed is the matrix

B; from the result:

0if,

(,)

(,) (, 1) if ,

tst ts

≤

⎧

⎨

−

−>

⎩

(4.16)

we get:

Using the relation

0if ,

(,)

(,) if ,

Hst

Qst i j

≠

⎧

⎪

⎨

⎪

⎩

∑

(4.17)

we finally obtain the matrix

The elements of this matrix represent the probability of leaving the state i in the

time that goes from s to t. They have sense only on the main diagonal of each

submatrix.

The matrix

D representing the probabilites of remaining in the state from the time

s up to the time t is obtained in the following way:

(,) (,)

tst

−DIH. (4.18)

For the last step, we have to compute the matrix

Φ , the solution of the evolution

equation of the DTHSMP whose element ( , )

represents the probability that a

taxicab driver being at time s in the zone i will be at time t in state j.

Discrete time SMP and numerical solution 149

Here, it can be verified that any row of the submatrix ( , )

tΦ is indeed a

probability distribution.

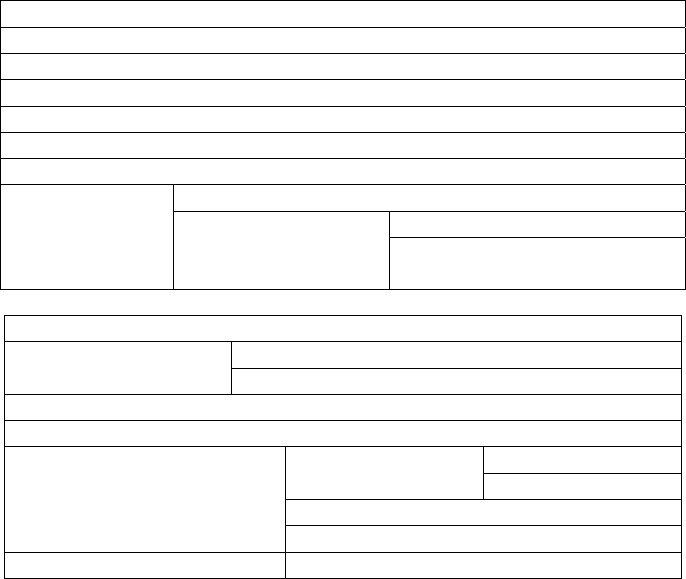
Matrix

(0,1)

Φ (0,10)Φ (0,20)Φ

0.9696 0.0255 0.0049 0.7936 0.1307 0.0757 0.6196 0.2089 0.1715

0.0123 0.9686 0.0191 0.1149 0.7845 0.1006 0.2473 0.5132 0.2395

0.0115 0.0046 0.9839 0.0862 0.1053 0.8085 0.2002 0.2142 0.5856

(5,6)Φ (5,15)Φ (5,25)Φ

0.9898 0.0084 0.0018 0.7812 0.1290 0.0898 0.5840 0.2421 0.1739

0.0213 0.9685 0.0102 0.1374 0.7324 0.1302 0.2551 0.5364 0.2085

0.0164 0.0157 0.9679 0.1153 0.1147 0.7700 0.2069 0.2375 0.5556

(10,11)Φ (10, 21)Φ (10, 31)Φ

0.9672 0.0242 0.0086 0.7275 0.1620 0.1105 0.5121 0.2971 0.1908

0.0201 0.9646 0.0153 0.1415 0.7095 0.1490 0.3241 0.4443 0.2316

0.0055 0.0057 0.9888 0.1254 0.1206 0.7540 0.2678 0.2726 0.4596

(20,21)Φ (20,26)Φ (20,31)Φ

0.9892 0.0034 0.0074 0.7926 0.1583 0.0491 0.5561 0.3145 0.1294

0.0186 0.9718 0.0096 0.1277 0.8174 0.0549 0.2883 0.6075 0.1042

0.0289 0.0095 0.9616 0.1287 0.0781 0.7932 0.2420 0.2192 0.5388

(25,26)Φ (25,28)Φ (25,32)Φ

0.9724 0.0096 0.0180 0.7794 0.1644 0.0562 0.4170 0.4360 0.1470

0.0715 0.9141 0.0144 0.1079 0.8313 0.0608 0.2924 0.5670 0.1406

0.0252 0.0009 0.9739 0.0552 0.0277 0.9171 0.2422 0.2194 0.5384

(29,30)Φ (29,31)Φ (29,32)Φ

0.8975 0.0661 0.0364 0.7097 0.2161 0.0742 0.4500 0.4351 0.1149

0.0246 0.9532 0.0222 0.1911 0.7463 0.0626 0.2827 0.5960 0.1213

0.1264 0.0287 0.8449 0.1378 0.0702 0.7920 0.1824 0.1675 0.6501

In the non-homogeneous case we report only the final results, the interested

reader can find them in the internet site given in the introduction.

5 CONTINUOUS AND DISCRETE TIME REWARD

PROCESSES

In this part we will present undiscounted and discounted semi-Markov reward

processes.

Reward processes can be seen as a class of stochastic processes. In the non-

homogeneous case it is possible to write more than 200 different evolution

equations of Semi-Markov ReWard Processes (SMRWP). We develop only three

150 Chapter 4

cases, the simplest and the most general. For a wider approach the reader can

refer to Janssen-Manca (2006).

5.1 Classification And Notation

5.1.1 Classification Of Reward Processes

In this book we will apply semi-Markov processes mainly in finance, insurance

and reliability problems. In all these fields, the association of a sum of money to

a state of the system and to a state transition assumes great relevance. In general,

this can be done by attaching a reward structure to the process.

This structure can be seen as a random variable associated with the state

occupancies and transitions (Howard (1971) vol. 2).

The rewards can be of different kinds, but in this book we will, because of our

kind of applications, consider only amounts of money. These amounts can be

positive, if for the system they can be seen as a benefit and negative if they can

be considered as a cost.

The reward processes can be seen as classes of stochastic processes that we can

classify in different cases. The following tables report the classification of the

SMRWP.

Process classification

Homogeneous

Non-Homogeneous

Continuous time

Discrete time

Non-discounted

Fixed interest rate

Homogeneous interest law

Discounted

Variable interest rate

Non-homogeneous interest

law

Reward classification

Time fixed rewards

Homogeneous rewards

Time variable rewards

Non-homogeneous rewards

Transition (impulse) rewards

Immediate

Discrete time

Due

Permanence (rate) rewards

Independent on next transition

Dependent on next transition

Discrete time SMP and numerical solution 151

We will not present permanence rewards that depend on the next transition

because in financial and insurance environments they do not have sense.

In general the distinction between homogeneous and non-homogeneous cases is

done for stochastic processes. Also an interest rate law can be defined as

homogeneous if the discount factor is a function only of the length of the

financial operation, non-homogeneous if the discount factor takes into account

also the initial time of operation, not only the duration.

In the same way, rewards can be fixed in time, can depend only on the duration

or can be non-homogeneous in time.

We will use the following notation:

,(),(,)

ii i

tst

ψψ

: represent rewards given for permanence in state i; the first is

time fixed, the second changes because of time and the third represents a time

non-homogeneous permanence reward.

,(),(,)

ij ij ij

tst

γγ

: represent the three different kinds of rewards given for the

transition from state i to state j (impulse reward).

In the discrete time case, the immediate case means that the reward is paid at the

end of each period; in the due case the reward is paid at the beginning of the

period. The impulse rewards

represent lump sums that are paid at the

transition instant.

5.1.2 Financial Parameters

To study the process with discounting, let us recall some basic results for

computing present values of amounts of money, annuities and also the related

notation.

For more details, refer to Volpe di Prignano (1985) or Kellison (1991).

Fixed time interest rate:

(1 )re

−−

=+ = : represents the one-period discount factor, where r is the

interest rate and

the corresponding intensity,

11 1

;,;

tt t

tr tr t

vr e

aada

rdr

−

−− −

====



represent the present value of

respectively a unitary annuity-immediate, an annuity-due and a continuous time

annuity,

11 1

aa a

∞∞ ∞

== =



represent the present value of infinite time unitary

annuities, also called perpetuities.

152 Chapter 4

Time variable interest rate:

Now we suppose that the interest rates are variable and depend on the time

period.:

()

() (1 ) , ()

krke

ττ

νν

−

∫

=+ =

∏

represent the k-period discount factor at

time 0 respectively in discrete and continuous time. They give, at time 0, the

discounted value of one monetary unit to be paid at the end of period k,

() (), () (), ()()

iii

kk kk d

ψνψψϑνϑϑ

−

∑∑

∫

represent the present value

respectively of an annuity-immediate, an annuity-due and a continuous annuity

with variable rewards in the time and variable interest rate on a time horizon t.

The infinite rates cases are given by the limit to

∞

of the three relations. They

converge depending on the values of and

()

(,) (1 ) , (,)

st r st e

ττ

νν

−

∫

=+ =

∏

represent the ts

−

period discount

factor at time s, with homogeneous interest rates giving, at time s, the discounted

value of one monetary unit to be paid at the end of period k, respectively in

discrete and continuous time,

(,) (,), (,) (,), (,)(,)

iii

ks ks

ksk sksk s sd

ψνψψϑνϑϑ

−

=+ =

∑∑

∫

represent the present

value at time s respectively of an annuity-immediate, an annuity-due and a

continuous annuity paid on the time interval

(

]

t with non-homogeneous

rewards and variable interest rate.

(,)

(,) (1 ) , (, )

st r s e

ττ

ννϑ

−

∫

=+ =

∏



represent the ts

−

period discount

factors at time s, with non-homogeneous interest rates,

(,) (,), (,) (,), (,)(,)

iii

ks ks

ksk sksk s sd

ψνψψϑνϑϑ

−

=+ =

∑∑

∫



represent the present

value at time s respectively of an annuity-immediate, an annuity-due and a

continuous time annuity paid on the time interval

(

]

t with non-homogeneous

rewards and non-homogeneous interest rate.

In the following sections, we will show that annuities are strongly related to the

semi-Markov reward processes; for the Markov case see Janssen-Manca (2006).

A reward structure can be considered as a very general structure that, given a

financial and economic meaning can be very useful in stochastic modelling.

For example, this behaviour is particularly efficient to construct models useful to

follow the dynamic evolution of insurance problems. In this case, the

Discrete time SMP and numerical solution 153

permanence in a state usually involves the payment of a premium or the receipt

of a claim. Furthermore often the transition from one state to another induces

some other cost or benefit.

5.2 Undiscounted SMRWP

For each given case we will present the immediate, the due and the continuous

cases, both in homogeneous and non-homogeneous environments. We will give

first the simplest case (only with permanence rewards and fixed rate of interest

and rewards) and after the general ones. The same cases will be given for

discounted processes.

5.2.1 Fixed Permanence Rewards

We assume that:

a) rewards are fixed in time,

b) rewards are given only for permanence in the state.

First we present the immediate case.

()

(

(,)

Vst

) represents the Mean Total Reward (MTR) paid or received in t

periods (from time s to time t), given that at time 0 (at time s) the system was in

state i.

At time 1 the evolution equation for the homogeneous immediate case is given

by the following relation:

()

110

(1) 1 (1) (1) ( ) (1 )

iiiikiikk

VH b bV

ψϑϑ

===

=− + + −

∑∑∑

. (5.1)

To have a good understanding of the evolution equation, let us first say that

relations (1.8) and (1.11) imply that

(1) (1)

ij ij

and so relation (5.1) can be

decomposed in the following way:

1110

(1) 1 (1) (1) ( ) (1 )

mmm

iikiikiikk

kkk

VQQQV

ψϑϑ

====

⎛⎞

=− + + −

⎜⎟

⎝⎠

∑∑∑∑

(5.2)

where (0) 0, and (0) 0 ,

kik

VkQik

∀=∀, and so:

(1) .

(5.3)

For the next step, we can write that:

11 11

(2) (1 ( )) 2 ( ) ( ) (2 ).

iiiikiikk

VHt b bV

ϑϑ

ϑψϑ ϑ ϑ

== ==

=− + + −

∑∑ ∑∑

(5.4)

This time, two rewards must be paid but in different ways. We divide the

evolution equation in three parts.

- the term (1 ( )) 2

−

represents the rewards obtained without state changes;

154 Chapter 4

- the expression

()

ik i

ψϑ

∑∑

gives the rewards obtained before the change of

state. As (0) 0 ,

bik=∀ , the sum on

begins from 1;

- the double sum

() (2 )

ik k

−

∑∑

gives the rewards paid or earned after the

transitions.

For time t, we get the following general result:

11 11

() (1 ()) ( ) ( ) ( ).

mt mt

iiiikiikk

Vt H t t b b V t

ϑϑ

ϑψϑ ϑ ϑ

== ==

=− + + −

∑∑ ∑∑

(5.5)

The general formula in the non-homogeneous case is:

(,) (1 (,))( ) (, )( )

(, ) ( ,).

iiiiki

ik k

Vst H st t s b s s

bs V t

ϑϑ ψ

ϑϑ

==+

=− − + −

∑∑

(5.6)

In this simple case the due and the immediate processes correspond. So we report

only the continuous cases.

()

() 1 () ( ) ( ) ( )

iiiiik ikk

Vt Ht t Q d Q V t d

ψϑϑϑ ϑϑϑ

=− + + −

∑∑

∫∫



, (5.7)

()

(,) 1 (,) ( ) (, ) ( )

(, ) ( ,) .

ii iiik

ik k

Vst H st t s Q s sd

Qs V td

ψϑϑϑ

ϑϑϑ

=− ⋅− + ⋅−

∑

∫

∑

∫



(5.8)

5.2.2 Variable Permanence And Transition Rewards

Here we assume that:

a) rewards are variable in time,

b) rewards are given for permanence in the state and at a given transition,

Under these hypotheses, we get respectively for homogeneous and non-

homogeneous environments, in the immediate cases the following results:

1111

11 11

()(1())() ()()

() () () ( ),

tmt

iiiiki

mt mt

ik ik ik k

Vt H t b

bbVt

τϑτ

ϑϑ

τϑψτ

ϑγ ϑ ϑ ϑ

====

== ==

=− +

++−

∑∑∑∑

∑∑ ∑∑

(5.9)

Discrete time SMP and numerical solution 155

1111

11 11

(,) (1 (,)) () (, ) ()

(, ) ( ) (, ) ( ,).

tmt

iiiiki

sks

mt mt

ik ik ik k

ks ks

Vst H st b s

bs bs V t

τϑτ

ϑϑ

τϑψτ

ϑγ ϑ ϑ ϑ

=+ = =+ =

==+ ==+

=− +

∑∑∑∑

∑∑ ∑∑

(5.10)

In the due case we obtain:

1111

11 11

() (1 ()) ( 1) ( ) ( 1)

() () () ( ),

tmt

iii iki

mt mt

ik ik ik k

Vt Ht b

bbVt

τϑτ

ϑϑ

ψτ ϑ ψτ

ϑγ ϑ ϑ ϑ

====

== ==

=− −+ −

++−

∑∑∑∑

∑∑ ∑∑



(5.11)

111

11 1 11

(,) (1 (,)) ( 1) (, ) ( )

(, ) ( 1) (, ) ( ,).

tmt

iii ikik

sks

mt mt

ik i ik k

ks ks

Vst H st b s

bs bs V t

τϑ

ϑτ ϑ

ψτ ϑγ ϑ

ϑψτ ϑ ϑ

=+ = =+

==+ = ==+

=− −+

+−+

∑∑∑

∑∑ ∑ ∑∑



(5.12)

The difference between immediate and due is given only by the time of payment

of the rewards.

The continuous cases are the following:

()

000

() 1 () ( ) ( ) ( )

() ( ) () ,

iii iki

ik k ik

Vt Ht d Q dd

QVt d

ττ ϑ ψττϑ

ϑϑγϑϑ

=− +

+−+

∑

∫∫∫

∑

∫



(5.13)

()

(,) 1 (,) () (, ) ()

(, ) ( ,) ( ) .

iii iki

sss

ik k ik

Vst H st d Q s dd

Qs V t d

ττ ϑ ψττϑ

ϑϑγϑϑ

=− +

∑

∫∫∫

∑

∫



(5.14)

The presence of the lump sums given or taken at the moment of transition times

is taken into consideration.

5.2.3 Non-Homogeneous Permanence And Transition Rewards

In the last immediate case model, the rewards are non-homogeneous and so we

have to consider only the non-homogeneous case.

Assumptions are thus:

a) rewards depend on the times s and t,

b) permanence and transition rewards are non-homogeneous.

Here, only the non-homogeneous case has sense and the evolution equations take

the form:

156 Chapter 4

1111

11 11

(,) (1 (,)) (,) (,) (,)

(, ) (, ) (, ) ( ,).

tmt

iii iki

skss

mt mt

ik ik ik k

ks ks

Vst H st s b s s

bs s bs V t

τϑτ

ϑϑ

τϑψτ

ϑγ ϑ ϑ ϑ

=+ = =+ =+

==+ ==+

=− +

∑∑∑∑

∑∑ ∑∑

(5.15)

1111

11 11

(,) (1 (,)) (, 1) (, ) (, 1)

(, ) (, ) (, ) ( ,).

tmt

iii iki

sks

mt mt

ik ik ik k

ks ks

Vst Hst s b s s

bs s bs V t

τϑτ

ϑϑ

ψτ ϑψτ

ϑγ ϑ ϑ ϑ

=+ = =+ =

==+ ==+

−−+ −

∑∑∑∑

∑∑ ∑∑



(5.16)

()

(,) 1 (,) (, ) (, ) (, )

(, ) ( ,) (, ) .

iii iki

sss

ik k ik

Vst H st s d Q s s dd

Qs V t s d

ττ ϑ ψ ττϑ

ϑϑγϑϑ

=− +

∑

∫∫∫

∑

∫



(5.17)

The other non-discounted cases can be treated in a similar way and are left to the

reader, who can refer also to Janssen-Manca (2006).

5.3 Discounted SMRWP

For the discounted case developed in this section, we assume that all the rewards

are discounted at time 0 in the homogeneous case and at time s in the non-

homogeneous case. Let us point out that these models, as we will see below, are

very important for insurance applications.

5.3.1. Fixed Permanence And Interest Rate Cases

In the first formulation of this case we suppose that:

a) rewards are fixed in time,

b) rewards are given only for permanence in the state,

c) interest rate r is fixed.

In this case

()

represents the Rewards Mean Present Value (RMPV) paid or

received in a time t, given that at time 0 the system is in state i.

Under these hypotheses, a similar reasoning as before leads to the following

result for the evolution equation, firstly for the homogeneous immediate case:

()

11 11

111

(1) 1 (1) (1) ( ) (1 ) ,

iiiikiikki

VH b bV

νψν ϑϑνψν

===

=− + + − =

∑∑∑

(5.18)

11 11

() (1 ()) ( ) ( ) ( ) .

mt mt

iiiikiikk

tr r

Vt H t a b a b V t

ϑϑ

ϑψ ϑ ϑν

== ==

=− + + −

∑∑ ∑∑

(5.19)

For the non-homogeneous case, this last result becomes: