Jackson S.D., Hargreaves J.S.J. Metal Oxide Catalysis
Подождите немного. Документ загружается.


8.4 Calculation of Surface Structure 355
It is normal to set the cell vector lengths based on the bulk optimized structure
at the level of theory to be used in the slab calculations. This choice gives lattice
parameters with zero strain in the bulk which is a likely constraint on the surface
repeat unit.
The surface energy is given by the equation:
E
EE
A
s
slab bulk
=
−
2
(8.26)
where E
slab
and E
bulk
are the energies for the slab model and that for an equivalent
amount of the bulk structure and A is the surface area of one side of the slab. Care
must be taken to obtain these energies at the same level of theory including basis
set quality and k - point sampling. A refi nement of Equation 8.26 to obtain surface
energies based only on slab calculations is also discussed below.
The whole point of the slab model is to reproduce an isolated surface so that
overlap of electron density between the slab and its periodic images must be
vanishingly small. This means that k - point sampling used to describe interactions
between unit cells in the direction perpendicular to the surface can be
achieved with a single k - point. In the directions parallel to the surface, however,
k - point sampling comparable to the reference bulk calculation must be
maintained.
8.4.1.1 Electrostatic Stability of Surfaces
Early on in the simulation of the surfaces of ionic materials Tasker [81] pointed
out that surface structure and stability depend not only on the Miller index of the
plane exposed but also the point at which the “ cut ” of the bulk is made [82] . This
can be illustrated by considering the examples shown in Figure 8.11 . Figure 8.11 a
shows the rock salt structure of MgO with the ion sizes set using the values from
Shannon ’ s tabulation [83] . The {001} planes are the faces of the cubic unit cell.
Looking at the stacking of ions perpendicular to any of these surfaces it is clear
that layers are stoichiometric and so charge neutral. Moving from the surface into
the bulk we pass through identical neutral layers which are simply offset from one
another by half a lattice vector in a direction parallel to the surface. In this case
any cut of the unit cell to create a surface will expose the same square two -
dimensional repeat unit, (Figure 8.11 b).
On electrostatic grounds, Tasker argued that surfaces made up of neutral layers
should be expected to be stable and referred to examples in which atomic layers
are neutral in this way as type I. Indeed the crystal habit of MgO is usually cubic
with {001} faces dominant.
In more complex structures, cuts at different points in a unit cell will lead to
very different surface terminations. For example, the corundum structure shown
in Figure 8.11 c and typifi ed by α - Al
2
O
3
, has a hexagonal unit cell. The atom layer-
ing perpendicular to the (0001) surface follows an Al - O - Al - Al - O - Al - Al . . . sequence.
In this case, cutting between two Al layers results in a stacking in which three

356 8 Theory: Periodic Electronic Structure Calculations
Figure 8.11 Examples of the effect of surface
cuts on the character of an oxide surface.
(a) The rock salt unit cell of MgO with ions
drawn in proportion to ionic radius (Mg
2+
0.72 Å , O
2−
1.40 Å ) From ref. [83] (b) Plan
view of the MgO(001) surface, generated by
taking the face of the cubic unit cell. (c) The
hexagonal unit cell of the corundum structure
typifi ed by α - Al
2
O
3
. A non - polar (001) surface
can only be generated by cutting between Al
3+
layers such as the cut indicated by the plane.
(d) Plan view of the surface termination for
the non - polar α - Al
2
O
3
(0001) surface, dotted
lines indicate the surface 2 - D unit cell which
shares the
a
and
b
lattice vectors (arrows)
with the bulk structure. (e) The two possible
(111) cuts for rock salt structures such as
MgO. Either one will lead to a polar surface.
(f) The O terminated (111) surface of MgO.
Magnesium, green; oxygen, red; aluminum,
pink.

8.4 Calculation of Surface Structure 357
layers (Al - O - Al) form a stoichiometric set of ions which is charge neutral and non -
dipolar with the surface structure shown in Figure 8.11 d. However, a different
choice of cut, say between Al and O layers to expose an oxygen only surface, would
result in a stacking sequence running (O - Al - Al - ) - (O - Al - Al - ) - (O - Al - Al - ), with brack-
ets indicating stoichiometric sets of layers. Clearly this choice of cut results in a
dipolar repeating unit into the bulk and so the electrostatic energy in a purely ionic
model will be divergent. This type of Miller plane, for which the choice of cut
determines stability, is referred to as a type II surface.
Finally, in cases such as the (111) surface of MgO, alternating layers of anions
and cations are obtained in the stacking sequence, Figure 8.11 e. Here there are
two choices of cut, one of which exposes a purely O
2 −
surface (Figure 8.11 f) and
one exposing purely Mg
2+
. Either will produce a dipolar slab. This is an example
of a type III surface which, on a purely electrostatic basis, is unstable and so should
not be observed experimentally unless stabilized by adsorbates or reconstruction.
Indeed LEED analysis has been used to show that the apparent occurrence of the
MgO(111) surface under vacuum conditions can be explained by microfacets of
{001} [84] .
8.4.1.2 The Effect of Slab Dimensions
It is important to test the validity of the slab model to reproduce the surface prop-
erties of isolated surfaces. The two main parameters are clearly the vacuum gap
introduced and the thickness of the slab employed. Both of these are system
dependent but Figure 8.12 shows the effect of the vacuum gap on the calculated
surface energy for the unrelaxed surface of α - Al
2
O
3
taken from localized basis set
GGA - DFT calculations using the DSOLID code. At small gap distances the surface
energy is underestimated, since in the limit of a zero vacuum gap Equation 8.26
would give E
s
= 0. The surface energy in this case is clearly converged above a
Figure 8.12 The variation of calculated surface energy for the
bulk termination of α - Al
2
O
3
(0001) with the vacuum gap used
in the slab geometry calculation. Adapted from ref. [30] .

358 8 Theory: Periodic Electronic Structure Calculations
vacuum gap distance of 10 Å . In plane - wave basis sets the vacuum gap is particu-
larly important as the number of plane - waves required for a given accuracy
increases with the simulation cell size and so a larger gap will require more com-
putational time.
The convergence of the surface energy with slab thickness for α - Al
2
O
3
has been
studied by Ruberto and coworkers [85] . They point out that early work on the use
of slabs to calculate the surface energy of simple metals showed that if a single
cell bulk reference energy is used in Equation 8.26 the surface energy diverges
with slab thickness [86] . The argument starts by considering a series of slab cal-
culations in which the number of stacking layers perpendicular to the surface is
increased systematically. Then we may expect the calculated surface energy to vary
according to number of layers, n , so that Equation 8.26 becomes
En
A
EnnE
sslabbulk
()
=
()
−
()
1
2
(8.27)
where the reference bulk calculation is for the equivalent amount of material used
for a single layer slab. At suffi ciently large values of n the surface energy should
converge so that:
En En
ss
()
=−
()
1
(8.28)
which implies,
EnnE En n E
slab bulk slab bulk
()
−
()
−−
()
−−
()
()
=11 0
(8.29)
so that an alternative way to estimate E
bulk
is to rearrange Equation 8.29 to
read
EEnEn
bulk slab slab
=
()
−−
()
1
(8.30)
Since this expression must be consistent with the slab calculations in terms of
basis set, number of k - points and so on it provides a more reliable value than does
a separate calculation of the bulk cell, which must have at least a different cell
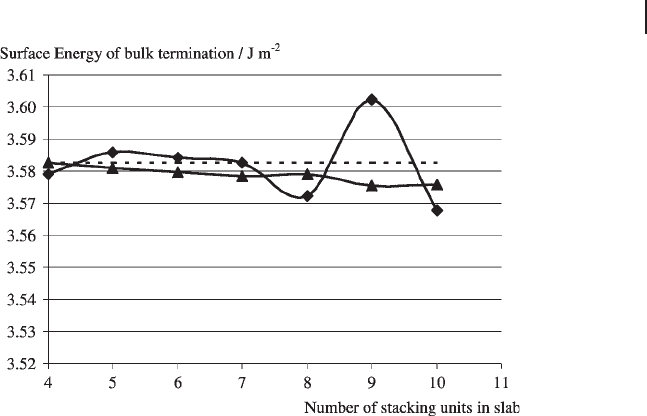
volume. The results obtained by Ruberto and coworkers [85] using the PW91
functional and a plane - wave basis set within the DACAPO code are plotted in
Figure 8.13 . For this type II surface the stacking layer is a single Al - O - Al unit, and
in this plot we compare the surface energy calculated using E
bulk
estimated from
Equation 8.30 and the result of taking E
slab
(10) − E
slab
(9) and using that value for
E
bulk
in Equation 8.26 for all slabs. In the latter case the result appears to have less
variation than the recipe outlined above. However, the trend is for this method to
diverge gradually away from the average, whereas the second method oscillates
around it. These oscillations are ascribed to quantum - size effects by Ruberto and
coworkers [85] .
8.4 Calculation of Surface Structure 359
8.4.2
Surface Calculations on MgO , Al
2
O
3
and TiO
2
There are few experimental estimates of surface energies and so most compari-
sons between simulation results and laboratory data are confi ned to surface struc-
ture. One exception is MgO{100}, which is formed from stoichiometric layers and
was used as an example of a type I surface (Figure 11 a and b). The MgO{100}
planes are fl at and charge neutral and so are easy cleavage planes for single crystal
samples. This allows estimates for the surface energy to be made from the mea-
sured work required to cleave a sample [87] . This data has the advantage that it is
free of errors arising from surface contamination. However, it does require large,
perfect crystals and so there is only data available for favorable cases, such as
MgO{100}. Estimates have also been made by comparing the heat capacities of
powder samples with those of large crystallites [88] . This approach depends on the
crystal habit of MgO, which is cubic, exposing only {100} surfaces.
Another possible reference is high - level correlated electronic structure methods
such as quantum Monte Carlo ( QMC ) simulations [89] . Alfe and Gillan have used
this approach to estimate the difference between DFT calculated surface energies
and QMC values for the slab energies of MgO(100) [90] . The QMC value obtained
for the surface energy lies in the range quoted from experimental cleavage values
(Table 8.5 ). They fi nd that LDA gives much closer agreement with this limiting
value than do GGA calculations. For example the PBE functional underestimates
Figure 8.13 The surface energy for the unrelaxed (0001)
surface of α - Al
2
O
3
using the method of Ruberto and
coworkers [85] (diamonds) and with a constant estimate of
E
bulk
( triangles). The average of the fi rst method is included as
a dotted line.

360 8 Theory: Periodic Electronic Structure Calculations
the surface energy by around 30%, which is consistent with the difference between
LDA and GGA found for TiO
2
and SnO
2
by the same group [91] . QMC is a highly
accurate method for obtaining the electronic structure of materials, but is also very
expensive in terms of computer time. For this reference calculation, relaxation of
the surface structure was carried out at the LDA level and the resulting co -
ordinates used in a one - off calculation of the system energy using QMC. Since the
relaxation of the MgO(100) surface is extremely small this leads to only small
errors for this case. For example, Table 8.5 gives the surface energy from Alfonso
and coworkers [92] and Skorodumova and coworkers [50] who report values calcu-
Table 8.5 Examples of type I, MgO(100), and type II, α - Al
2
O
3
(0001),
surface energies and relaxations.
Surface Method Layers
a)
E
s
( J m
− 2
) E
s
(J m
− 2
) ∆ Z
d)
(%)
Reference
unrel.
b)
rel.
c)
MgO (100) LDA 5 – 1.24 – [90]
PBE 5 – 0.87 – [90]
QMC 5 – 1.19 – [90]
LDA 3 1.39 1.38 2.2 [92]
LDA 7 1.16 1.14 2.27 [50]
PW91 7 0.92 0.90 2.27 [50]
Expt.
e)
1.04 – 1.20 [87]
Expt.
f)
1.09 – 1.36 [88]
α - Al
2
O
3
(0001)
LDA 3 3.77 1.76 [93]
LDA 6 – 1.95
− 77
[94]
LDA 1.98
− 85
[95]
LDA 10 3.97 1.94
− 86
[85]
PW91 10 3.58 1.60
− 86
[85]
PW91 6 – 1.98
− 84
[96]
PBE 6 – 1.72
− 92
This work
Expt.
g)
− 51
[79]
Expt.
h)
− 63
[97]
Expt.
i)
− 50
[98]
a Number of non - polar stacking units used in slab. For MgO(100) this is an atomic layer while for
α - Al
2
O
3
(0001) it is an Al
–
O
–
Al tri - layer. Many papers study the convergence with number of
layers; the largest value used is quoted here.
b Value for unrelaxed bulk termination at a non - polar cut.
c Value after geometry optimization.
d For MgO(100) the rumpling of the surface given by Equation 8.31 ; for α - Al
2
O
3
(0001) the
displacement perpendicular to the surface of the outermost Al ion with respect to the fi rst O layer
on relaxation of the bulk terminated structure.
e Estimated from work required to cleave crystal.
f Calorimetric measurements on powders extrapolated to 0 K.
g Grazing incidence X - ray diffraction.
h TOF - SARS.
i LEED - IV ( Low Energy Electron Diffraction, Intensity/Voltage analysis ).

8.4 Calculation of Surface Structure 361
lated from both unrelaxed and relaxed slab calculations with LDA and PW91
functionals. The effect on the energy of optimizing the surface structure is only
0.01 – 00.02 J m
− 2
, which is, at most, around 2%.
For the relaxed surface, the interlayer spacing is hardly changed from the {100}
bulk values. However, small surface rumpling does occur on slab optimization in
which, for MgO at least, O
2 −
ions move to positions further from the slab center
than the Mg
2+
ions. This can be quantifi ed by calculating the dimensionless
quantity:
∆
∆
Z
ZZ
Z
rum
OMg
L
=
−
(8.31)
in which Z
O
and Z
Mg
are the Z co - ordinates (assuming Z is perpendicular to the
surface) of the O
2 −
and Mg
2+
ions at the surface of the relaxed slab and ∆ Z
L
is
the interlayer spacing in the bulk structure. The values given in Table 8.5 are in
the range 2.2 – 2.3% and so the effect is quite small. Interestingly, CaO(100) shows
a negative ∆ Z
rum
, of around the same magnitude, indicating that the metal ions
move away from the bulk termination into the vacuum gap while the anions move
toward the bulk in this case. Skorodumova and coworkers suggest that this is due
to the greater repulsion between the semi - core electrons of the cation and the
O(2p) states for the larger cation [50] .
We saw from the bulk studies that α - Al
2
O
3
is the most crystalline form of
alumina and so many calculations have focused on this form for surface calcula-
tions. The most stable surface in the hexagonal setting is (0001) which was illus-
trated as a type II surface in Figure 8.11 . Manassidis and Gillan [93] have considered
this surface using the LDA, fi nding a surface energy of 1.76 J m
− 2
(Table 8.5 ). This
is lower than found in later calculations at the LDA level by Ruberto and coworkers
[85] , Finnis and coworkers [94] and Di Felice and Northrup [95] , who all fi nd
surface energies around 0.2 J m
− 2
higher. This may be due to the rather thin slab
that was used by Manassidis and Gillan, with only three non - polar stacking units
compared to 6 – 10 in the later calculations. Owing to the computational restrictions
of the computers available at the time, Manassidis and Gillan could only test con-
vergence for the unrelaxed slab with the ions at their bulk positions. In contrast
to the MgO(100) example, relaxation of the α - Al
2
O
3
(0001) slab geometry causes a
dramatic lowering of the surface energy by around 2 J m
− 2
, that is, over 50%. It is
clear that in this case the slab thickness will become important. Indeed in the
study by Ruberto and coworkers it was found that the center of the slab showed
negligible relaxations only for the thickest slabs used, which contained 9 or 10
tri - layers.
Marmier and Parker [96] using PW91 within the VASP program found a surface
energy which is close to the converged LDA results using a six tri - layer slab. This
would be unexpected from the observations made earlier suggesting that GGA
surface energies tend to be lower than LDA. Comparing values calculated by dif-
ferent research groups is always diffi cult; however, the consistent set of calculations
on thicker slabs by Ruberto and coworkers do give a GGA surface energy around
362 8 Theory: Periodic Electronic Structure Calculations
20% lower than their LDA result. Our own PBE calculation on a six tri - layer slab
also gives a lower surface energy than the LDA results reported in Table 8.5 .
Marmier and Parker also calculated the surface energy of six additional non - polar
surfaces, confi rming that the (0001) is the lowest energy. The other surfaces in
order of calculated surface energies were
0112
()
,
1123
()
,
1120
()
,
1010
()
,
1011
()
and
2243
()
with values of 2.04, 2.25, 2.34, 2.56, 2.57 and 2.77 J m
− 2
respectively.
Based on these relative energies it is possible to predict crystal morphology by
creating a Wulff plot in which low - energy surfaces are assumed to form the domi-
nant crystal facets. The predicted morphology from Marimier and Parker ’ s calcula-
tions is compared with that from optical microscopy [99] in Figure 8.14 . There is
agreement on the importance of the (0001) surface. However the calculations
appear to overestimate the surface energy of the
1011
()
surface as this is a major
facet in the experimental structure but is relatively minor according to the GGA
calculations. They suggest that this could be due to microfaceting, where the
crystallite surface of this energetically unfavorable facet is actually made up of
many tiny steps expressing lower energy Miller planes. The same group success-
fully showed this to be the correct explanation for experimental observations of
the MgO(111) “ polar ” surface.
As already mentioned, the relaxation of the α - Al
2
O
3
(0001) surface results in
much more dramatic atomic displacements than are seen for MgO(001). For the
non - polar bulk termination, the outermost Al ion has three O neighbors (Figure
8.15 a) compared to the six found for the bulk site. On relaxation this Al atom
moves downward, becoming almost co - planar with the fi rst oxygen layer as shown
in Figure 8.15 b. This example calculation was carried out using the SIESTA
code with the PBE functional. The calculated lattice parameters for the hexagonal
unit cell of the bulk are slightly longer than the experimental reference structure
( a = b = 4.801 Å , c = 13.078 Å compared to a = b = 4.759 Å , c = 12.991 Å ) [23] . The
difference in the Z - co - ordinates (direction perpendicular to the surface) between
the surface Al and O layers decreases by 92%, from 0.836 Å to 0.063 Å . This is
accompanied by an expansion of the equilateral triangle formed by the three
nearest neighbor oxygen atoms to the outermost Al atoms. As a result the Al
–
O
bond distances on the surface change to a lesser extent, with Al
–
O in the bulk
termination being only 0.17 Å longer than in the relaxed surface (1.70 Å versus
1.87 Å ). This type of relaxation has been observed in many earlier calculations,
Figure 8.14 Comparison of the (a) calculated (from ref. [96] )
and (b) observed (from ref. [97] ) crystal habit of α - Al
2
O
3
.
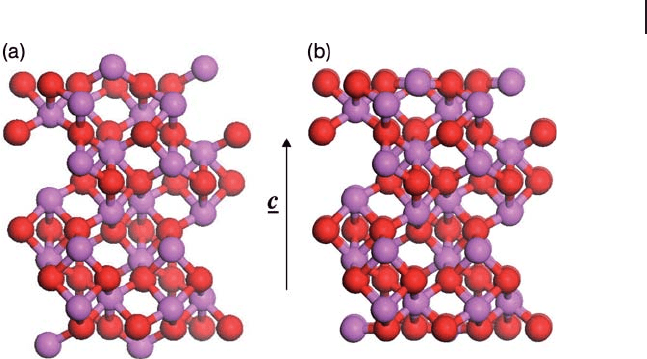
8.4 Calculation of Surface Structure 363
some of which are also listed in Table 8.5 . Our own calculation is on the high end
of the reported data, but for this illustrative example we used a relatively thin slab
and did not optimize the SIESTA basis set. Even so our value is in reasonable
agreement withthat of Ruberto and coworkers, who used the thickest slabs and
carefully considered the convergence of surface energy with simulation parame-
ters. HF and B3LYP methods have also been shown to give an inward relaxation
of around 80% in a systematic study of this surface by Gomes and coworkers using
the localized basis set code CRYSTAL with 15 layer two - dimensional periodic
simulations. They also show that using surface lattice vectors obtained from an
optimization of the structure at each level of theory is preferable to using the
experimental crystal structure parameters.
Experimentally, surface relaxation has been studied using time of fl ight scatter-
ing and recoil spectroscopy ( TOF - SARS ) [97] , glancing angle X - ray diffraction [79]
and LEED - IV [98] . All three techniques show the same inward relaxation, but the
percentage difference between the bulk termination and observed separation of
the outermost Al and O layers is only between 50 and 63%. This discrepancy may
be partly due to the diffi culty of eliminating H from the experimental surfaces.
The presence of H in hydroxyl groups changes the character of the outer layer by
increasing the effective co - ordination of the outermost Al atoms and reducing the
degree of relaxation considerably.
The electronic structure of the α - Al
2
O
3
(0001) surface also shows features that
differ from the bulk material [30] . Figure 8.16 compares the calculated DOS for
the dense phase with that of a slab calculation. In the DOS for the slab (Figure
8.16 b) a state just below the bottom of the conduction band can be seen which
Figure 8.15 A slab simulation of the Al
2
O
3
(0001) surface
consisting of six tri - layer units, viewed with surface running
into the page. A 10 Å vacuum gap in the c direction was used
to isolate periodic images. (a) Bulk non - polar termination.
(b) After relaxation of atom co - ordinates. Aluminum, pink;
oxygen, red.
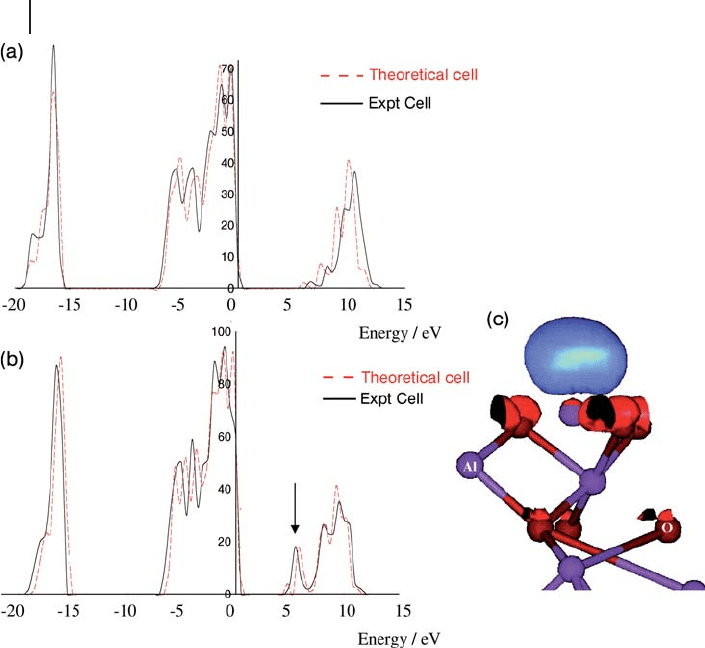
364 8 Theory: Periodic Electronic Structure Calculations
is not present in the bulk calculation (Figure 8.16 a). This is the lowest unoccu-
pied state in the system and the plot of the corresponding real space orbital in
Figure 8.16 c shows that it is localized at the surface and contains mainly Al s
and p orbitals combined to give a lobe perpendicular to the surface. This orbital
will be accessible to adsorbates and, since it is empty, will be involved in charge
transfer from surface species. This gives rise to Lewis acidity on the surface of
α - Al
2
O
3
.
One example that demonstrates the role of this type of Lewis acid site in surface
chemistry is a study of the mechanism of water dissociation over the clean α -
Al
2
O
3
(0001) surface by Hass and coworkers [100] . They used the BLYP functional
in the CPMD code to allow the free energy of dissociation to be estimated using
constrained dynamics [101] . The initial adsorption mode involves the coordination
Figure 8.16 Density of states calculated for (a) the bulk and
(b) the (0001) surface of α - Al
2
O
3
, using the localized basis
set code DSOLID with the PW91 functional, from ref. [30] . In
each case the solid line is calculated at the experimental
geometry while the dotted line is for the optimized cell.
(c) The lowest unoccupied state indicated by the arrow in (b).
