Jackson S.D., Hargreaves J.S.J. Metal Oxide Catalysis

Подождите немного. Документ загружается.

be solved by making an initial guess for the form of the molecular orbitals. These

are used to calculate F

, but are likely to alter when Equation 8.1 is solved so that

the contributions of J

and K

to F

will also be changed. A new estimate of the

Fock operator can then be made from the new solutions and used in turn to gener-

ate a new set of molecular orbitals. This process is repeated until the molecular

wavefunctions no longer alter from one cycle to the next, that is, a self - consistent

set of molecular orbitals is obtained.

In practical problems, the molecular orbitals themselves are constructed using

the idea of a linear combination of atomic orbitals or, more generally, a linear

combination of basis functions, χ

φχ

iijj

∑

(8.3)

where the coefﬁ cient, c

, sets how much of basis function, χ

, to include in the i

molecular orbital. It is these coefﬁ cients that are obtained via the self - consistent

solution of Equation 8.1 . Usually the number of atomic functions used in the basis

set of a calculation is more than the total number of occupied atomic orbitals in

the free atoms. The extra ﬂ exibility this introduces into the basis set allows features

such as polarized bonds and weak intermolecular interactions, such as hydrogen

bonding, to be better represented.

8.2.1.1 Exchange Energy

When discussing the electronic structure of molecules and solids, one - electron

descriptions, such as the molecular orbitals of Equation 8.1 , are quite intuitive. It

is common to talk about individual electrons occupying particular states. For

example, reactions often occur by the mixing of the highest occupied molecular

orbital ( HOMO ) of one species and the lowest unoccupied molecular orbital

( LUMO ) of another. In such a reaction the electrons in the HOMO state move

into the new mixed orbital, lowering their energy. The HOMO and LUMO states

are each pairs of one - electron molecular orbitals, since in the simplest case an

orbital giving the spatial distribution for a spin up electron has an identical partner

for spin down. Multi - electron wavefunctions that describe the whole electronic

structure in this picture are constructed from the one - electron states. So, for

example, in a four - electron system in which all the electronic states are doubly

occupied (spin up and spin down), based on Hartree – Fock theory we can write:

Ψ rrrrrrrr

14 122

4221

...

()

() () () ()

−

() ()

φφφφ φφφ

αα

ββ

αα

223

ββ

αα

ββ

φφφφ

rrrr

() ()

(

() () () ()

)

...

(8.4)

That is, the multi - electron wavefunction is formed from products of molecular

spin orbitals. Here, φ

()

means the j

electron with co - ordinate r

is in the i

molecular orbital with β spin. The spin should be thought of as an additional

8.2 Electronic Structure Methods 325

326 8 Theory: Periodic Electronic Structure Calculations

co - ordinate that takes on one of two values for each electron ( α spin up and β spin

down, say). Having the spin states explicitly separated in this way allows the energy

levels for α and β spins to differ and is referred to as unrestricted Hartree – Fock

( UHF ). In many cases the spatial part of the orbitals are the same for α and β spin

and so it is computationally cheaper to calculate only a single set of spatial func-

tions and assign pairs of spin up and spin down electrons. However, this is a

constraint on the orbital energies and so is referred to as restricted Hartree – Fock

( RHF ). The dotted line in Equation 8.4 means that additional terms are actually

included but not written here for clarity. The multiple terms must be included so

that the electrons remain indistinguishable from one another. In fact there will

be 24 terms in all, with every permutation of electrons in molecular spin orbitals

included, hence the normalization factor of

14! . The terms in Equation 8.4 are

generated following the rule that if any two electrons are swapped the sign of the

multi - electron wavefunction should change. These anti - symmetrized wavefunc-

tions are often written in the more compact form of Slater determinants [5] . To

calculate the electron – electron interaction energy in this system we form integrals

of the type:

Err

rrr r

141 4

()()

−∞

∞

∫

... ... ...ΨΨ*dd

(8.5)

where the superscript “ * ” is used to indicate the complex conjugate of the wave-

function and 1/ r

is the Coulomb operator for the interaction between electrons i

and j which are a distance r

apart. The integration is over all electron co - ordinates

and over all space and can be carried out by substituting from Equation 8.4 into

Equation 8.5 . At ﬁ rst sight, even for our four - electron example, this should give a

set of 576 integrals over the molecular spin orbital products to evaluate. This is

quickly reduced to 275 since electron i with j is duplicated by j with i and electron

self - interactions can be ignored. In addition only certain types of these integrals

are non - zero. Each integral contains all four electron co - ordinates, but the operator

in Equation 8.5 only affects electrons 1 and 2, so that the other electrons can be

treated separately. Through the normalization conditions required of molecular

orbitals, electrons 3 and 4 will simply give factors of 1 in integrals of products for

which they are in the same molecular spin orbital on either side of the operator.

When they are in different orbitals to left and right their orthogonality gives 0.

This leaves only 12 terms in which electrons 1 and 2 are in the same spin orbitals

on either side of the operator, such as:

Jrr

rrrr

12 1122

11 22 1 2

() () () ()

−∞

∞

∫

φφ φφ

αα αα

(8.6)

which is the Coulomb integral giving the electrostatic repulsion between the elec-

tron density of electron 1 in molecular orbital 1 with that of electron 2 in molecular

orbital 2. A factor of 2 occurs here because electrons 3 and 4 can be either way

round in orbitals 3 and 4. We say “ terms such as ” because the form of Ψ ( r

. . . r

)

means we will also obtain Coulomb integrals for electron 1 in orbital 2 and electron

2 in orbital 3 and so on. There are actually 12 terms in total and the role of the

normalizing factor in ensuring no over - counting takes place can now be seen.

Expressions such as Equation 8.6 are Coulomb integrals because each electron is

in the same molecular orbital to the left and to the right of the operator in J .

However, there is another type of term that arises from Equation 8.5 :

Krr

rrrr

12 1 2 2 1

11 22 1 2

=−

() () () ()

−∞

∞

∫

φφ φφ

αα αα

dd (8.7)

The exchange integral is a consequence of the condition that electrons are indis-

tinguishable, which leads to Equation 8.4 for the multi - electron wavefunction. It

has the opposite sign to the Coulomb integral because of the anti - symmetry prop-

erty of multi - electron wavefunctions; we still require electrons 3 and 4 to remain

in the same molecular orbitals to the left and right of the operator, that is, there

has only been one exchange.

For electrons of different spin the Coulomb integral will work in the same way,

but the exchange integral becomes:

−

() () () ()

−∞

∞

∫

212

φφ φφ

rrrrdd (8.8)

This result occurs because the electron spins have changed from left to right of

the operator and so integration over the spin degrees of freedom gives zero. This

important result means that the exchange energy is only relevant to electrons with

the same spin.

HF theory is built on the idea of one - electron states and makes the integrals

tractable by assuming that each electron experiences the average or mean ﬁ eld of

all the others in the system. Then it is possible to solve for the one - electron states

by taking the potential of each electron including a contribution from the Coulomb

and exchange integrals following Equation 8.2 . All other electrons in the system

are averaged out using their one - electron wavefunctions in the J and K integrals.

As mentioned earlier, altering the wavefunction of an electron in response to this

potential changes the energy of all the other one - electron states and so the elec-

tronic structure has to be solved iteratively until a self consistent condition is

reached.

8.2.1.2 Correlation

The HF approach gives an exact treatment of the exchange interaction between

electrons. However, because it uses the mean ﬁ eld approximation, it ignores the

effect of the Coulomb interaction on the relative positions of the electrons at

8.2 Electronic Structure Methods 327

328 8 Theory: Periodic Electronic Structure Calculations

any instant. Electron motion is correlated, as can easily be seen from the form

of the anti - symmetrized wavefunctions, Equation 8.4 . Imagine that electron 1

and electron 2 move to exactly the same co - ordinate in space, that is, r

= r

. If

this were to happen, all pairs of terms with electron 1 and electron 2 exchanged

in Ψ ( r

. . . r

) would cancel out and the wavefunction collapse to zero. This means

that the probability of two electrons occupying the same point is zero and the

electron motion must be correlated to ensure that no two electrons

with the same spin arrive at the same coordinate. This correlation leads to the

so - called Fermi hole. If we plot the wavefunction as a function of the electron –

electron separation it must go to zero at r

= 0. At larger distances the Coulomb

repulsion between the electrons will also affect their correlated motion. In HF

theory, this correlation caused by Coloumb repulsion is ignored through use of

the mean ﬁ eld approximation implicit in the J and K integrals. Correlation will

tend to result in electrons avoiding one another more than would be expected

from the mean ﬁ eld approximation and so HF over - emphasizes the electron –

electron repulsion.

Correlation can be re - introduced into wavefunction - based theories through

perturbation methods (such as M ø ller – Plesset [6] MP2 or MP4) or the mixing in

of excited - state multi - electron wavefunctions (the conﬁ guration interaction ( CI )

methods [7] ). However, currently the computational cost of these calculations in

periodic simulations is too great for their widespread use. In molecular simulation,

MP2 has been used for some time and its importance in describing the long - range

correlation required for van der Waals interactions of alkanes with zeolites has

recently been pointed out [8] .

8.2.2

Density Functional Theory ( DFT )

DFT is based on the notion that the electron density is uniquely deﬁ ned by the

external potential, which for a molecule or condensed solid is simply the interac-

tion potential with the constituent nuclei. This was put forward as the Hohen-

berg – Kohn theorem [9] which states that the ground - state electron density ρ

(r)

minimizes the energy functional, E [ ρ ( r )], which for a system of electrons interact-

ing with nuclei is given by:

Er Fr

ρρ

()

[]

()

[]

−

()

−

−∞

∞

∫

∑

(8.9)

where F [ ρ ( r )] is a universal functional that has to account for the kinetic energy

of the electron density and the electron – electron interaction. These terms are

“ functionals ” because the energies depend on the entire function ρ ( r ) rather

than its particular value at a particular point in space. In principle, the

ground - state energy and electron density may be found using a variational mini-

mization of the electron density ρ ( r ), a process which scales linearly with the

system size. This is much more attractive than HF theory because the number of

Coulomb and exchange integrals increases rapidly with the number of electrons

considered.

The form of F [ ρ ( r )] is crucial for any successful application of DFT. Kohn and

Sham postulated [10] that F [ ρ ( r )] can be written:

Fr Tr

rrE rρρ

ρρ

()

[]

()

[]

()

′

()

−

′

()

[]

−∞

∞

−∞

∞

∫∫

SXC

(8.10)

where the ﬁ rst term T

[ ρ ( r )] is the kinetic energy of a system of non - interacting

electrons with density ρ ( r ) and the second is the classical electron – electron

Coulomb interaction, playing the role of the J integrals discussed for HF theory.

However, instead of multiple integrals over electron co - ordinates, we now have a

simpler double integral over the electron density. The ﬁ nal term, E

[ ρ ( r )], is the

exchange - correlation energy, which has the simple deﬁ nition in DFT that it must

compensate for the use of non - interacting electron states in the kinetic energy and

include the exchange and correlation factors discussed above.

Progress is usually made by writing the electron density in terms of a set of

one - electron wavefunctions, ψ

, such that;

ρψψrr r rr

()

() ()

∑

(8.11)

The sum is over all occupied orbitals and d

r is an inﬁ nitesimal volume. As in the

HF case these spatial orbitals will have an associated spin component for each

electron. These one - electron wavefunctions are just a convenient way to represent

the density during the calculation and so we have used a new symbol to distinguish

them from the one - electron HF molecular orbitals. They are actually for a ﬁ ctitious

system of non - interacting electrons that is made to have the same density as the

interacting electron system we are interested in. This gives a straightforward

method to obtain the kinetic energy term and allows E [ ρ ( r )] to be minimized with

respect to ρ ( r ) using a basis set representation of the one - electron wavefunctions,

via the set of equations,

−∇ +

()

iiii

Vr r r

eff

ψεψ (8.12)

for each state i , where V

eff

is an “ effective potential ” ;

Vr Vr

rV r

eff ext XC

()

′

()

−

′

()

−∞

∞

∫

(8.13)

and V

( r ) is the exchange - correlation potential obtained from

∂

()

The only

constraint on this process is that the integral of ρ ( r ) over all space is constant since

this is ﬁ xed by the number of electrons in the system.

8.2 Electronic Structure Methods 329

330 8 Theory: Periodic Electronic Structure Calculations

These equations map the problem of a system of interacting electrons onto a

system of non - interacting electrons moving in an effective potential. The behavior

of the exchange - correlation potential as a function of the electron density is a

complex problem. The interactions it represents can be long - range in nature, so

even if the “ correct ” form of E

were known, its calculation would be as complex

as the post - HF methods mentioned at the end of the previous section. To make

DFT practical and efﬁ cient, approximations for E

are introduced.

The simplest approach, known as the Local Density Approximation ( LDA ),

deﬁ nes E

as:

Er r rr

XC XC

hom

dρρερ

()

[]

() ()

[]

−∞

∞

∫

(8.14)

where ερ

hom

()

[]

is the exchange - correlation energy per unit volume of a homo-

geneous electron gas of density ρ ( r ). The exchange contribution for ερ

hom

()

[]

can be calculated exactly but the correlation requires a reference calculation using

a high - level method. The use of the homogeneous electron gas (external potential

zero everywhere) allowed a very accurate calculation to be carried out by Ceperley

and Alder using quantum Monte Carlo techniques [11] . The resulting data has

been parameterized to analytical functions by Vosko, Wilk and Nusair [12] and

by Perdew and Wang [13] . Computer implementation of the LDA and its exten-

sion to a spin unrestricted form LSDA (in which the densities for spin up and

spin down electrons are allowed to differ) depend on these parameterized forms

of ερ

hom

()

[]

In the LSDA approach, the exchange and correlation are calculated purely based

on the density at each point in the system, assuming that these quantities will be

the same as in a uniform gas of electrons with the same density. This is only really

the case when the electron density is a slowly varying function of position, such

as in the valence states of the alkali metals [14] . Despite this, LSDA has been found

to give useful insights in a wide range of solid - state systems, including metal

oxides.

Ideally we would like to also include the longer range correlation effects, and a

ﬁ rst step toward this is using functionals that depend not only on the local density

but also on the gradient of the density. The gradient of the density is also a local

property but gives information on how the density is varying in the immediate

vicinity of a given point. Functionals of this type fall under the generalized

gradient approximation ( GGA ) and simply add terms depending on the gradient

of the electron density to the parameterization of E

. Although GGAs do not

offer a consistent improvement over LDA in all types of system, they have been

shown to improve on the LDA for calculations of molecular structures and bond

energies [15] . There are many different approaches to the form and parameteriza-

tion of a GGA and these are given acronyms based on the names of the people

who derived them. Among the most widely used are PBE ( Perdew, Burke

and Ernzerhof ) [16] , and its revision based on surface calculations revised PBE,

RPBE [17] , PW91 ( Perdew and Wang 1991 ) [18, 19] and BLYP ( the exchange func-

tional of Becke [20] with correlation functional from by Lee, Yang and Parr ) [21] .

In the remainder of the text we shall use these acronyms without further

referencing.

In the LSDA and GGA approaches, the Coulomb integrals are calculated on the

same footing as in HF theory, but using the Kohn – Sham orbitals. However, the

exchange contribution is taken from a functional of the density and so the interplay

of the Coulomb and exchange energies, which is clear under the HF approach, is

not so well balanced in DFT. In particular, using V

based on the density in

Equation 8.12 implies that each electron contributes to its own potential, the so

called self interaction problem.

To look into this, hybrids between DFT and HF have been introduced. In this

approach, the HF exchange expression is used with the Kohn – Sham orbitals,

mixing “ exact - exchange ” ,

exact

, with conventional GGAs, in the general form;

EEaEE aEaE

hybrid

LSDA

exact

LSDA

GGA

=+ −

()

∆∆ (8.15)

where E

LSDA

is the exchange and correlation energy according to the LSDA, the

bracketed term is a correction to the exchange energy from the difference between

exact and local density exchange and the ﬁ nal two terms are gradient corrections

along the lines of the GGA. The three parameters a

, a

and a

can be set against

experimental reference data for small molecules. In Becke ’ s original paper [22] ,

PW91 was used for the GGA correlation part of Equation 8.15 and a ﬁ t to 56

atomization energies, 42 ionization potentials, 8 proton afﬁ nities and 10 total

atomic energies gave parameter values of a

= 0.20, a

= 0.72 and a

= 0.81. One

of the most ubiquitous hybrid functions, also based on this approach, is named

B3LYP, with the “ 3 ” referring to the number of parameters. This replaces the GGA

correlation in Becke ’ s scheme with the functional of Lee, Yang and Parr men-

tioned above.

Hybrids give signiﬁ cant improvement over GGAs for many molecular proper-

ties and are widely used in studies of metal complexes and homogeneous catalysis

[23] . They have been more slowly adopted in solid - state chemistry than in the

molecular area because of the difﬁ culty of computing the exact - exchange part

within the plane - wave basis set approach discussed below. However, as we will

see, in the simulation of oxides they give an improvement in the relative energies

of ﬁ lled and empty states and have advantages in problems for which electron

localization has to be described.

It should be remembered that DFT is designed to reproduce the ground - state

density of the system under consideration. It is not concerned with excited states

and so the relative energy of ﬁ lled and empty orbitals is not as well deﬁ ned as in

the HF approach. We will see that, in solid - state calculations, this results in a poor

estimation of the band gap for insulators when using LSDA or GGA functionals.

To tackle excitations directly, the more computationally demanding time -

dependent DFT methodology has been developed and this does allow spectro-

scopic excitation energies to be calculated [24] .

8.2 Electronic Structure Methods 331

332 8 Theory: Periodic Electronic Structure Calculations

8.2.3

Periodic Quantum Chemistry

8.2.3.1 Band Theory

In a crystal, the wavefunctions and density are formally of inﬁ nite extent and so

to represent the wavefunctions using the linear combination of atomic orbitals

familiar from molecular quantum mechanics would require an inﬁ nite basis set.

Such an approach is clearly impractical; however, the periodicity of the system

suggests that only the unit cell of the lattice is really required. This, with some

provisos outlined below, is indeed the case. A very comprehensive discussion of

band theory and the implementation of periodic DFT has been published by Payne

and coworkers [25] , and more recently Hill and coworkers have produced a book

covering background theory and applications in materials science [26] . In this

section we give an overview of the methodology that takes the molecular orbitals

of isolated species into the band states of solids.

Firstly, note that it is the electron density that is observed experimentally in X -

ray diffraction ( XRD ) experiments and so is used to deﬁ ne the unit cells of cry-

stalline solids. In a periodic system, this means that the electron density has to

have the same repeat distance as the lattice in all directions. Bloch ’ s theorem

points out that the restriction this imposes on the underlying wavefunctions is

actually less rigorous since the relationship between electron density, ρ ( r ), at an

arbitrary point, r , and the one - electron wavefunctions obtained from calculations

(HF or DFT) is:

ρψψrr r rr

()

() ()

∑

(8.16)

for an N electron system. This is similar to Equation 8.11 except that we have

assumed that spin up and spin down states have the same spatial distribution and

are occupied pairwise. A correctly periodic density can be achieved by writing the

wavefunctions as the product of a function with the same periodicity as the lattice,

( r ), and a function which varies on a longer length scale:

ψχ

jk j

exp=

()

⋅

()

(8.17)

where i is the square root of − 1 and

deﬁ nes a reciprocal space vector:

ka b c=++

abc

***

(8.18)

is the number of cells in the sample along the a - direction with N

and N

the

number along b and c respectively, l, m and n are integers with ranges set by the

corresponding N value,

−≤<NlN

22 and so on. In Expression 8.18 reciprocal

space vectors are indicated by a superscript “ * ” . These are related to the real space

lattice vectors via:

abc

bca

cab

=×

(8.19)

The function χ

( r ) in Equation 8.17 can be thought of as the periodic extension

of the basis functions used in molecular orbital problems. For example, in an

oxide in which there is a single oxygen ion in the unit cell the set of O(2s) func-

tions repeated throughout the lattice would form a suitable χ

( r ). One possible

Bloch state is simply to set

= (0, 0, 0) which would give neighboring O(2s) orbi-

tals in phase with one another and so there would be a bonding interaction for

this orbital across the unit cell boundary. Another possible solution is that O(2s)

orbitals in adjacent cells have an anti - bonding interaction. This is obtained along

the a lattice vector direction for

= (

* /2, 0, 0), which for the O(2s) orbitals must

give a higher energy solution than

= (0, 0, 0). The N

, N

and N

values in (18)

tend to be large, tending to inﬁ nity, so that the variable

is virtually continuous.

This means that the energy of the Bloch states between these extremes, of

= (0,

0, 0) (all bonding along a ) and

= (

* /2, 0, 0) (all anti - bonding along a ), will vary

smoothly.

The plot of energy against

is the dispersion for the band and gives the variation

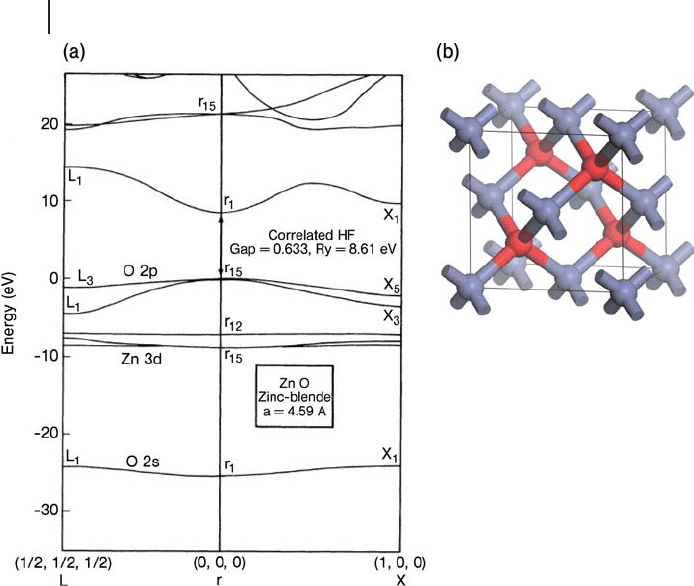
in energy for each local cell orbital. An example plot for ZnO in the zinc blende

structure is shown in Figure 8.1 a. This band structure was produced using a HF

calculation with correlation corrections introduced from separate cluster calcula-

tions [27] . Although ZnO occurs naturally in the hexagonal wurtzite structure, the

cubic cell of zinc blende (Figure 8.1 b) was used in this study of the effect of the

local environment of the Zn

cation on the band structure and provides a simple

illustration of the features of a dispersion plot. The three - dimensional nature of

reciprocal space means that the values of

that are plotted in band - structure dis-

persion plots can only give a representative variation of the band energies along

particular paths. These paths are usually chosen to include the maxima and

minima that occur at special points where the

vector has a simple relation to the

reciprocal space vectors. The special point

= (0, 0, 0) is always labeled Ã . In Figure

8.1 a, moving to the right of the Ã point ends at the special position

= (1, 0, 0),

labeled X. Along this path only h has been varied in Equation 8.18 . The zinc blende

structure is based on the cubic unit cell shown in Figure 8.1 b and so the reciprocal

space cell is also cubic and the three directions [1 0 0], [0 1 0] and [0 0 1] are

equivalent. Hence, there is no need to show the dispersion along paths directly to

Y or Z. To the left of the Ã point in Figure 8.1 a the plot ends at

= (1/2, 1/2, 1/2),

8.2 Electronic Structure Methods 333

334 8 Theory: Periodic Electronic Structure Calculations

labeled L , so the path taken involves increasing each of l, m and n in Equation 8.18

by the same amount.

Figure 8.1 also illustrates that the band width depends on the χ

( r ) function being

used in the Bloch states (17). The O(2s) orbital is the lowest energy atomic orbital

and forms a low - lying band with little dispersion, that is, the band width is small.

This orbital is relatively tightly bound to the atomic core and the overlap between

O(2s) orbitals in neighboring unit cells will be small. The O(2p) orbital on the

other hand is more diffuse and so the overlap between neighboring cells leads to

a calculated band width of around 5 eV.

The smooth variation of energy with

means that the whole band structure can

be interpolated from a ﬁ nite number of

- points. The total energy of the system

can then be estimated by integrating over the occupied portion of the band struc-

ture. To this end, computationally efﬁ cient methods for sampling

in three

dimensions taking advantage of lattice symmetry have been proposed and are

widely used [28] . The convergence of calculations with the number of

- points is

an important check that should be made at the start of a simulation project. As

an example, Table 8.1 shows the variation in the calculated total energy for MoO

as a function of the k - point sampling grid. Here the total energy per unit cell is

Figure 8.1 (a) The calculated dispersion curves for ZnO in the

zinc blende structure. From ref. [27] . (b) The zinc blende unit

cell. Zinc, blue; oxygen, red.