Jackson S.D., Hargreaves J.S.J. Metal Oxide Catalysis

Подождите немного. Документ загружается.

calculated using a gradient - corrected DFT technique so that the energy quoted

corresponds to the total energy of the valence electrons per unit cell. The bulk

MoO

lattice parameters are a = 3.963 Å , b = 13.855 Å and c = 3.696 Å [29] , so that

the

lattice vector is signiﬁ cantly longer than

. This means that orbital

overlap is expected to be weaker in the b direction than in a or c and correspond-

ingly the dispersion in the band moving along

* is less. Hence the number of

grid points required in the

* direction is fewer than in

* or

* . From Table 8.1

we can see that the energy of the bulk is converged to a precision of 10

− 3

eV (or

0.1 kJ mol

− 1

) for a

- point grid of 5 × 3 × 5 .

This idea that large unit cell dimensions in real space require fewer samples to

be taken in reciprocal space can also be useful when working with supercells. A

supercell calculation uses multiple crystallographic cells as the repeated simula-

tion unit. For example, in calculations on surfaces this allows reconstruction on a

length scale longer than is allowed by the minimal unit cell. The sampling of

reciprocal space in supercell calculations can be reduced because multiple

- points

of the normal unit cell can be represented in real space. This idea is illustrated in

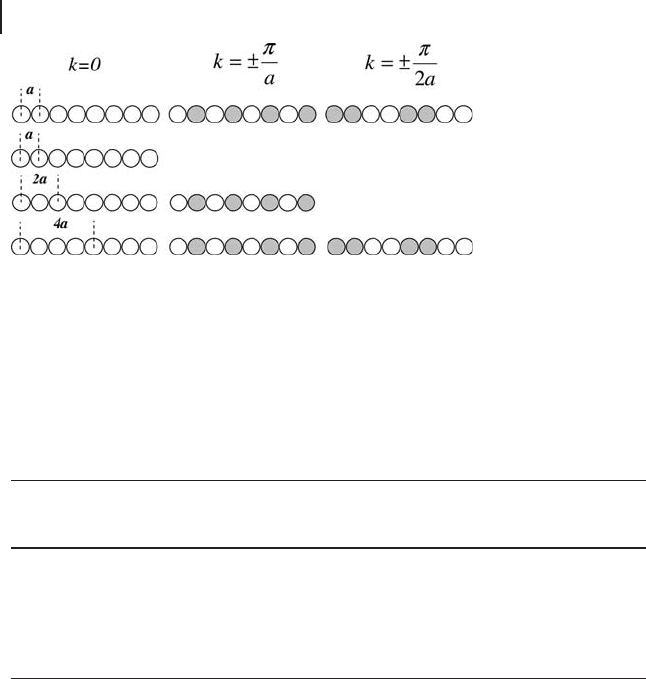
Figure 8.2 using a one - dimensional example with a single s - orbital per site. In the

minimal unit cell sampling at k = ± π / a corresponds to a wavefunction with phase

alternation between neighboring sites (in one dimension a * = 2 π / a ), which is at

the top of the band. If we use a supercell with a length of 2 a this wavefunction

can be represented with k = 0 because there are now two possible cell orbitals. The

total number of orbitals has not changed, but in the new cell one band would be

formed from the state with neighbors in the same phase and a different band

would be formed with neighboring states out of phase. The third state shown at

the top of the diagram would still require a reciprocal space point away from k =

0, as its repeat length is longer than 2 a. Doubling the cell once more allows all

three states to be represented in real space.

Table 8.1 Convergence of the bulk energy for MoO

, with respect

to the k - point grid using a planewave basis ( E

cut

= 520 eV) and

PBE functional within the VASP code.

k - point grid

MoO

bulk energy (eV)

∆E

(eV)

3 × 1 × 3 − 130.168 980

–

3 × 3 × 3 − 130.171 210

0.002 230

5 × 3 × 5 − 130.271 510

0.100 300

7 × 3 × 7 − 130.272 620

0.001 110

9 × 3 × 9 − 130.272 710

0.000 090

11 × 3 × 1 1 − 130.272 680

0.000 030

15 × 5 × 1 5 − 130.272 680

0.000 000

a Grid quoted as number of points sampled in the

* ×

reciprocal lattice directions.

b ∆ E is the difference in energy between two consecutive k - point

grids.

8.2 Electronic Structure Methods 335

336 8 Theory: Periodic Electronic Structure Calculations

Figure 8.2 One - dimensional example of using supercells

to reduce k - point sampling. With a minimal unit cell of

dimension a , the states shown on the top line require 3 k -

points to be sampled. Doubling the unit cell allows the ﬁ rst

two states to be generated at k = 0; with a unit cell dimension

of 4 a all three states are contained within the local cell

wavefunctions.

This effect can be seen in calculations on real materials; Table 8.2 shows the

convergence of the binding energy per unit volume of α - Al

with cell size cal-

culated using gradient - corrected DFT with a localized basis set in the DSOLID

package [30] . The binding energy is with respect to DFT calculations on the neutral

atomic species and so the values quoted are considerably smaller in magnitude

than for the earlier MoO

example.

8.2.3.2 Basis Sets

A basis set is required to describe the cell periodic part of the Bloch function in

Equation 8.17 . It is possible to use localized functions based around the atomic

Table 8.2 The affect of unit cell size on calculated binding energy for α - alumina.

Multipliers for

a, b ( Å )

Formula of

repeating unit

Cell volume relative

to Rhomb. cell

Binding energy

per

unit volume (eV Å

− 3

)

Rhomb.

A l

− 0.6951

1,1

A l

− 0.7175

2,1

A l

− 0.7151

3,1

A l

− 0.7173

4,1

A l

1 2

− 0.7173

a The rhombohedral unit cell is the primitive cell; all other calculations employ the more usual

hexagonal unit cell.

b These structures were based on the experimental hexagonal unit cell with a = b = 4.759 Å ,

c = 12.991 Å and γ = 120 ° .

c Binding energy is deﬁ ned as the difference between the total energy of the unit cell and the sum

of total energies for the same neutral atoms in isolation. This is quoted per unit volume to allow

comparison of the differently sized cells.

orbital like the basis sets found in molecular quantum chemistry. This is the

approach used in the CRYSTAL [31, 32] code which employs Gaussian functions

for the radial part of the atomic orbitals. The codes SIESTA [33] , DMOL

(and its

predecessor DSOLID) [34] also use localized basis sets but store the radial decay

of the basis functions on a numerical grid. For the localized basis set, work has

also to be undertaken to optimize the functions used for the solid state, as the

radial decay proﬁ les used in molecular problems are usually not appropriate [35] .

For example, the O

2 −

ion is more diffuse than an oxygen atom in a molecule and

so the basis sets used for molecular quantum chemistry will not perform well. An

alternative approach is to use the periodic nature of the system to build the elec-

tronic wavefunctions as sets of plane - waves. Codes that take this avenue include

VASP [36] , DACAPO [37] and CASTEP [38] . The Carr Parinello molecular dynam-

ics code ( CPMD ) [39] is also a plane - wave code with the added feature that the

electronic degrees of freedom are included in the evolution of the system based

on Newton ’ s laws. The plane - wave basis is speciﬁ c to the solid state and so some

background is given in the following text.

Any function used as the local part of the wavefunction description must

be periodic in the cell dimensions. In a plane - wave basis this is ensured by

choosing a linear combination of plane - waves with particular reciprocal space

vectors:

jjG

cirGr

()

=⋅

()

∑

exp

(8.20)

in which the coefﬁ cient c

is the amount of the plane - wave with reciprocal wave

vector

to include in local function j. Each

vector is described by the

equations

GT T a b c⋅= = + +2πmuvw

(8.21)

that is, the vector dot product between an acceptable

vector and any real space

vector,

, which is a combination of real space lattice vectors ( u,v,w are integers),

gives an integral number of 2 π radians. Under this condition any two points in

the lattice that are separated by a vector such as

must have the same value of

(

). Note that the

vectors have a repeat which is contained within the unit cell

while the

- vectors used in the Bloch states of Equation 8.17 have periods on a

larger scale.

The use of plane - waves as a basis in this way is just like taking the Fourier

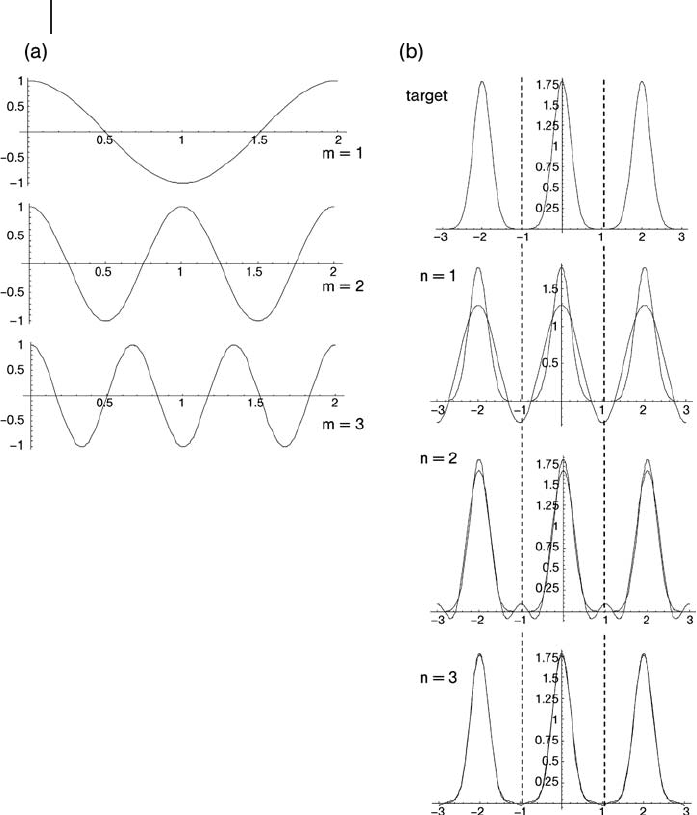
transform of a known function. A simple one - dimensional illustration of this is

shown in Figure 8.3 . Three waves which obey the periodic boundary condition

set by a unit cell of length 2 units ( m = 1 – 3 in Equation 8.21 ) are shown in Figure

8.3 a. The target function is a periodic set of Gaussians shown at the top of Figure

8.3 b. Since the target function is known, the coefﬁ cients, c

, can be calculated

analytically and the basis summed following Equation 8.20 . Figure 8.3 b shows

8.2 Electronic Structure Methods 337

338 8 Theory: Periodic Electronic Structure Calculations

Figure 8.3 (a) One - dimensional example of a plane wave

basis set for a unit cell of length 2 consisting of 3 functions.

(b) Application of the basis to generate a target function

which is a periodic set of Gaussians.

how the agreement between the target function and that constructed from the

plane - wave basis becomes better as the number of plane - waves used, n , is increased.

This Gaussian example is a particularly simple one because the function varies

quite smoothly with position, as do the plane - waves, and so after three basis func-

tions are included the match with the target is already very good. In a DFT calcula-

tion the target functions are not known and so the coefﬁ cients, c

, are solved for

as part of the self - consistent solution of the Kohn – Sham equations.

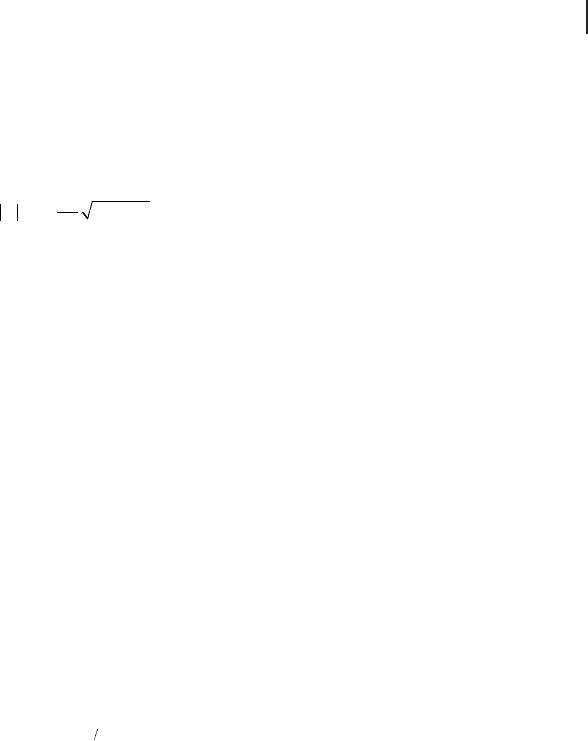
The plane - wave basis has the advantage that it can be systematically improved

by simply increasing the number of plane - waves used. The basis set is usually

truncated, based on an energy cut off, E

cut

, which deﬁ nes the kinetic energy limit

for the plane - waves. The corresponding maximum

vector is related to the energy

cut off via,

max

ecut

(8.22)

Here we have reverted to SI units so that m

(the electron mass) and h (the

Planck constant) appear in the formula. In most programs this |

max

value is used

along with Equation 8.21 to determine the number of plane - waves in the basis set

for the entire calculation by setting the maximum value of the integer, m. It has

been pointed out by Pulay that Equation 8.21 implies that the basis set is actually

dependent on the size of the unit cell, since

depends on the lattice vectors. This

can lead to additional stresses in calculations in which the cell volume is allowed

to vary. These appear because the quality of the basis set changes with cell dimen-

sions. In particular, when the volume of a unit cell is estimated using a plane - wave

basis, separate optimizations of the ions within a series of ﬁ xed volume cells is

more reliable than allowing the cell volume to be optimized during a single run.

The goal of periodic calculations is to generate a reliable estimate for the electron

density of the unit cell. However, many chemical concepts of bonding rely on ideas

that are not so easily deﬁ ned, such as atomic charges with which to quantify the

ionicity of the system. The expression for the electron density in terms of molecu-

lar orbitals Equation 8.16 does allow a partitioning of the charge density to be

undertaken to access such quantities. In terms of the basis set the density can be

re - written:

ρχχrr c r c rr

ji i

jk k

()

() ()

∑∑∑

(8.23)

where we have M functions in the basis set and c

is the coefﬁ cient for the expan-

sion of the i

basis function in the j

molecular orbital. Therefore the density is

actually built up from products of basis functions known as overlap functions. In

a localized basis set it is easy to assign basis functions to atoms, since each is based

on an atomic orbital belonging to a particular center. The basis functions belong-

ing to a particular atom, A , will appear in Equation 8.23 in some terms that involve

only functions centered on A and in some giving overlap with other centers. The

ﬁ rst set of terms are usually assigned as belonging wholly to A , but to assign a

particular portion of the density to atom A we must also take some component of

the overlap with other atoms. Mulliken [40] proposed that these overlaps between

different atomic centers be divided equally between the atoms involved, and this

estimate of the atomic charge is widely reported in the output of periodic electronic

structure codes. When a plane - wave basis set is used in the calculation the assign-

8.2 Electronic Structure Methods 339

340 8 Theory: Periodic Electronic Structure Calculations

ment of basis functions to particular atoms is not so straightforward. A way around

this is to use the plane - wave basis to do the calculation and then ﬁ t a local basis

representation to the resulting density and use the Mulliken analysis on that. The

ﬁ tting process is often referred to as the projection of the plane - wave calculated

density onto the localized basis set.

Mulliken analysis is a quick and relatively simple way to break down the charge

density into atomic contributions but it is dependent on the basis set used. In

particular, if the number of basis functions is unevenly distributed between atoms,

those with rich basis sets will tend to have too much charge assigned through the

Mulliken procedure. To attempt to rectify this, methods based on the charge

density alone have also been developed. For example, Bader analysis uses the

minima in the density to deﬁ ne a region around each atom over which the density

can be integrated numerically [41] .

8.2.3.3 Pseudopotentials

To describe the bonding between atoms, it is convenient to split the electrons for

each atom into valence and core states. In general, the core states are those not

directly involved in bonding interactions and the valence states are the outermost

atomic orbitals that can mix or otherwise interact strongly with neighboring atoms.

It is usual to replace the inﬂ uence of the core electrons of an atom on the valence

states by the use of pseudopotentials, that is, a function which represents the true

full electron potential in the valence region but varies more smoothly in the core

region of the atoms. In the valence region, the wave functions from calculations

using pseudopotentials and those with all electrons included should match closely.

In the core region, the smooth variation of the pseudopotential leads to a more

smoothly varying wavefunction. In essence, the radial nodes in the core region are

eliminated. To be resolved correctly, rapid spatial variation of core state nodes

would require a large number of plane - waves in the basis set; hence the use of

pseudopotentials reduces the number of plane - waves that have to be used in a

calculation while maintaining a good representation of the chemically important

valence states. An additional beneﬁ t for heavy elements is that relativistic effects

are more pronounced in the core region but their effect on the electrons in the

valence region can be reproduced by calibrating the pseudopotential against full

relativistic calculations on atoms. The valence electronic structure is then free to

use non - relativistic DFT.

Each pseudopotential is deﬁ ned within a cut - off radius from the atom center.

At the cut - off, the potential and wavefunctions of the core region must join

smoothly to the all - electron - like valence states. Early functional forms for pseudo-

potentials also enforced the norm - conserving condition so that the integral of the

charge density below the cut - off equals that of the all - electron calculation [42, 43] .

However, smoother, and so computationally cheaper, functions can be deﬁ ned if

this condition is relaxed. This idea leads to the so called soft and ultra - soft pseu-

dopotentials deﬁ ned by Vanderbilt [44] and others. The link between the pseudo

and real potentials was formalized more clearly by Bl ö chl [45] and the resulting

projector augmented - wave pseudopotentials have also been implemented in plane -

wave basis set codes [46] .

In oxides, the division between core and valence states should be carried out

with care. For example, in strongly ionic materials the cation may have lost all

valence electrons to the anion and so the cation/anion interaction involves orbitals

on the cation that are atomic “ core ” states. In this situation, explicit inclusion of

the outermost cation orbitals would be required for accurate results. Even so, the

replacement of the core region with a smoother potential can reduce the calcula-

tion time even for H atoms, and so pseudopotentials are available even in this

case.

For consistency, pseudopotentials should be based on the same functionals as

used for the valence states. This point has been illustrated by Gale and coworkers

in their study of aluminum trihydroxides [47] . Table 8.3 compares their results of

cell optimizations using various mixtures of psuedopotential and valence state

functionals with the experimental structure of gibbsite [48] . LDA pseudopotentials

in an LDA optimization of the cell gives underestimated cell parameters, consis-

tent with the usual expectation that LDA gives over - binding in chemical bonds.

This is partially corrected by switching just the valence states to the GGA func-

tional PBE, which is a fortuitous consequence of over - binding in LDA being

compensated for by under - binding in the GGA. If PBE is used for both pseudo-

potential and valence states, the

and

lattice vectors are over - estimated and the

best estimate for the

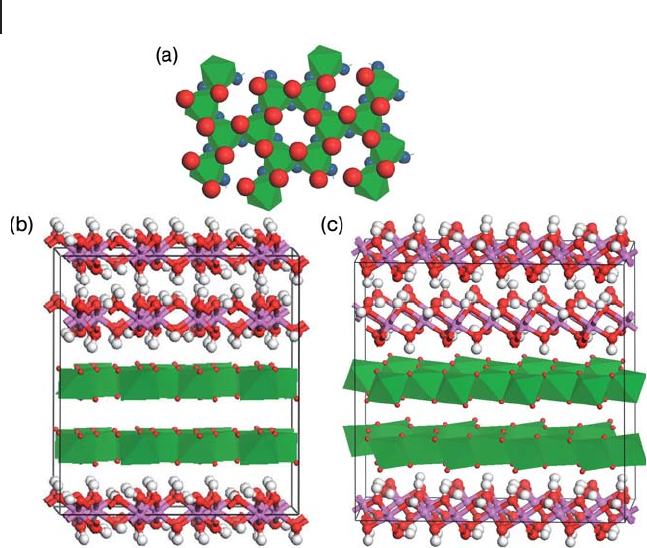
parameter is obtained. This structure is layered and held

together in the

direction by hydrogen bonding (see Figure 8.4 ). Using LDA/LDA

or LDA/PBE these hydrogen bonds are foreshortened, leading to underestimation

of the lattice vector. In the mixed case this means that a calculation using a GGA

in the valence states still performs like the LDA calculation because of the inﬂ u-

ence of the pseudopotential. The use of mixed functionals has also been found to

lead to large errors in the calculated binding energies of molecules to metal sur-

faces which are corrected by employing a pseudopotential consistent with the GGA

used for the valence states [49] .

Table 8.3 Optimized structural parameters for Al(OH)

(gibbsite)

using various functionals for the pseudopotential/valence states.

parameter LDA/LDA LDA/PBE PBE/PBE Expt.

a ( Å ) 8.504 8.623 8.798 8.684

b ( Å ) 4.867 5.017 5.110 5.078

c ( Å ) 9.224 9.598 9.674 9.736

β ( ° )

93.06 92.76 92.54 94.54

Cell vol. ( Å

) 381.2 414.7 434.4 428.0

Data taken from ref. [47] .

a Ref. [48] .

8.2 Electronic Structure Methods 341

342 8 Theory: Periodic Electronic Structure Calculations

8.2.3.4 Density of States

Within a band of states, the fact that

is virtually continuous means that the sepa-

ration between individual energy levels is vanishingly small. It makes no sense,

then, to try and draw a conventional energy level diagram of the type used in

molecular orbital calculations. The idea of a density of states ( DOS ) plot is to show

the number of states in a small energy interval as a function of state energy. The

number of states in a band per unit energy depends on the band width and the

number of cell - based functions that contribute to the band. The localized metal

cation d orbitals, for example, tend to give narrow bands with correspondingly

high density of states.

Figure 8.5 shows example calculated DOS plots for MgO and TiO

(rutile). In

both cases the zero of energy is taken as the highest occupied state which occurs

at the top of the upper valence band ( UVB ). The small tail on the UVB that indi-

cates some states with positive energy is an artefact of the smoothing process used

to construct the DOS plot from a calculation using ﬁ nite number of

- points. In

addition to the total density of states, a decomposition into states associated with

Figure 8.4 The structure of Al(OH)

aluminum hydroxides: (a) a layer of edge -

sharing octahedra taken from the bayerite

structure, oxygen atoms on top of this bi - layer

shown as large red spheres while those on

the underside are shown as small blue

spheres. (b) The structure of bayerite: two

bi - layers are shown in the polyhedra

representation of (a) with H atoms omitted

for clarity, the remainder of the structure is

shown with Al in pink, O in red and H in

white. (c) The structure of gibbsite using the

same representations as (b).

the oxygen and states associated with the metal atoms has been carried out. This

involves a projection of the density calculated using the plane - wave basis set onto

an atom localized basis of s, p and d functions. There is some arbitrariness in the

choice of this basis and so the absolute values of the partial density of states will

vary according to the choice made. In this case, we have relied on the PAW pseu-

dopotential functions used in the VASP code to deﬁ ne the localized basis set into

Figure 8.5 (a) The DOS for MgO and the

smearing function ( f ( E )) used for calculating

the state occupancy. (This has a maximum

value of 1.) (b) The DOS of TiO

(rutile). Both

calculations used the VASP code with PAW

pseudopotentials and the PW91 functional; a

Gaussian smearing of 0.2 eV has been used

for each calculated point in the DOS. Total

DOS shown as a solid line, partial DOS for O

dashed line and for the metal ions dotted

line, arbitrary units are used for the DOS

magnitude. LVB, lower valence band; UVB,

upper valence band; CB, conduction band.

8.2 Electronic Structure Methods 343

344 8 Theory: Periodic Electronic Structure Calculations

which the projection takes place. These technicalities aside the relative contribu-

tion of metal and oxygen orbitals in each band do give some qualitative informa-

tion on the character of bonding in the materials.

The plot for MgO (Figure 8.5 a) is typical of a main group metal oxide which ﬁ ts

with the classical ionic bonding model of oxide structures. The lower valence band

( LVB ) consists almost exclusively of O(2s) states and the UVB of O(2p) states. In

the conduction band ( CB ) both Mg and O basis functions contribute to the crystal

orbitals. The valence bands are completely ﬁ lled and, since they have mainly O

character, this corresponds to complete transfer of valence electrons from Mg to

O to give the ionic species Mg

and O

2 −

In the TiO

calculated DOS (Figure 8.5 b) the LVB is also mainly constructed

from of O(2s) orbitals but in the UVB the lowest energy states (between − 6 and

− 4 eV) are around 50 : 50 O and Ti in character with O(2p) orbitals being the major

constituent for higher energy states. In the conduction band the Ti orbitals make

up the larger part of the available states. The mixing of Ti and O states in the UVB

is consistent with a more covalent bonding model since electrons in these states

are shared between metal and oxygen atoms.

The width of the band formed is an indication of the degree of delocalization of

the band states and a comparison of Figure 8.5 a and b shows the biggest difference

in the UVB region. In the ionic model of MgO, the localization of electron density

on the O

2 −

ions leads to a relatively narrow UVB, while the covalent bonding in

TiO

gives rise to more delocalized states and so to a broader UVB.

This effect is also found for the bandwidth of the O(2p) bands for the alkaline

earth metal oxides which, at the LDA level of theory, decrease down the group

from a calculated value of 4.44 eV (MgO) to 1.83 eV (BaO). This is partly due to

the increase in lattice parameter, which spaces the O

2 −

ions more widely in BaO

than in MgO. However, in addition, it is found that the outermost valence elec-

trons for the metal ions interact more strongly with the O(2p) states in BaO than

in MgO, giving more localization of the electron density at O

2 −

and so a smaller

anion in BaO [50] .

Converging the self - consistent procedure in periodic calculations can be a difﬁ -

cult task, particularly if there are free states within any band. Movement of elec-

trons between almost identical states has little effect on the energy of the system

and so the search for the optimal distribution of electrons is hampered by many

trivial alterations to the occupation numbers. To make the process more efﬁ cient,

partial occupancies can be used for states near the highest ﬁ lled level by introduc-

ing a smoothing function which deﬁ nes the occupancy as a function of state

energy, E

. The smoothing function used in the MgO calculation was:

()

−

()

1exp

(8.24)

This expression is based on the statistical mechanics of electrons which have an

energy distribution given by Fermi – Dirac statistics [51] . The partial occupancy