Ирхин В.Ю., Ирхин Ю.П. Электронная структура, корреляционные эффекты и физические свойства d

Подождите немного. Документ загружается.

с ситуацией в 3d-периоде (структура оцк между Ti и Fe). Однако Sc и Ti (n

< 4)

имеют гпу (а не гцк) структуру, стабильность которой не описывается в терминах

- и e

-состояний.

Петтифор [253] вычислил энергии трех основных структур (гцк, оцк и гпу)

ряда 3d-металлов в рамках модельного псевдопотенциала с двумя параметра-

ми d-резонанса. Стабильность кристаллических структур как функция числа d-

электронов n

= n − 2 описывается следующей последовательностью

1-1.5 1.5-2 2-4.5 4.5-6.5 6.5-7.9

Structure гцк гпу оцк гпу гцк

Эти результаты соответствуют экспериментальной ситуации в 3d-ряде.

Скривер [245] оценил энергетические разности различных решеток в 3d, 4d и

5d-рядах и для редкоземельных элементов (Рис.3.12-3.16), а также для актинидов,

используя подход теоремы сил в методе ЛМТО. Результаты Петтифора были под-

тверждены, и общая последовательность гпу-оцк-гпу-гцк в других d-периодах была

также воспроизведена. Исследование стабильности кристаллических структур в ря-

де лантаноидов дало последовательность

гпу - типа Sm - двойная гпу - гцк - гцк

Тип решетки определяется числом 5d-электронов, которое изменяется от 2 (La) до

1.5 (Lu) (Рис. 3.14).

Одноэлектронные зонные вычисления [245] качественно согласуются с экспери-

ментальными данными и дают правильно кристаллическую структуру 35 металлов

из 42 исследованных (в частности, теория терпит неудачу для Au, Mn, Fe и Cо). Что

касается количественного согласия (значения параметров диаграммы состояния, на-

пример температур и давлений переходов), проблемы значительно более трудны,

так что удовлетворительные результаты были получены только для простых метал-

лов. Расчетные энергетические разности для d-металлов [245], оказываются в 3-5 раз

больше, чем разности энтальпии, полученные путем изучения бинарных диаграмм

состояния (Рис. 3.16).

Структура и энергия связи 5d-элементов были рассчитаны в [254] в рамках линей-

ного метода c орбиталями слэтеровского типа. Недавнее вычисление полных энергий

для 3d, 4d и 5d металлов [255] было выполнено скалярным (полурелятивистским)

РППВ-методом (в отличие от вычисления Скривера [245], приближение заморожен-

ного потенциала не использовалось). Выводы согласуются с результатами по ре-

шеточным параметрам и объемным модулям [24] и стабильности кристаллических

структур [245], так что релятивистские поправки оказываются не слишком важны-

ми. Экспериментальная структура Au также была получена в этом расчете.

Вычисления стабильности кристаллических структур, равновесного объема и

объемного модуля для легких актинидов Th, Pa и U в рамках метода полного по-

тенциала [256] дают хорошее согласие с экспериментальными данными.

3.3 Теплоемкость

В предыдущих разделах этой главы мы рассматривали энергетические характери-

стики кристалла, которые дают общее описание электронных и ионных систем. Здесь

мы рассмотрим удельную теплоемкость, которая позволяет получить более деталь-

ную информацию относительно электронного и решеточного спектра.

3.3.1 Решеточная теплоемкость

Исследование удельной теплоемкости играло важную роль в развитии квантовой

теории твердого состояния. Мы кратко напомним об основных результатах. Тепло-

емкость при постоянном объеме определяется на языке средней энергии

∂E

∂T

(3.19)

В классической картине каждая степень свободы частицы вносит вклад k

T/2 в теп-

ловую энергию. Тогда энергия трехмерного кристалла, который содержит N ионов

и n электронов, равна

E = 3Nk

T +

T (3.20)

(средняя энергия ионов, которые рассматриваются как осцилляторы, удваивается

из-за потенциальной энергии). Таким образом, решеточная удельная теплоемкость

одноатомного кристалла должна быть равна 3R (R = k

= 8.3 Дж/моль K -

газовая постоянная, N

- число Авогадро). Этот результат соответствует закону

Дюлонга и Пти, который был установлен для большого числа твердых тел. Одна-

ко экспериментально этот закон выполняется как правило в не слишком широкой

области около комнатной температуры. С уменьшением температуры c

уменьша-

ется, в согласии с общей теоремой Нернста, стремится к нулю при T → 0. С другой

стороны, c

значительно увеличивается при высоких T .

Квантовая теория решеточного вклада в удельную теплоемкость была развита

Эйнштейном (1906) и Дебаем (1910). Эйнштейн рассматривал кристалл как систему

независимых осцилляторов с постоянными частотами ω

. Тогда применение стати-

стики Бозе дает

E = 3N¯hω

(ω

) +

] (3.21)

где

(ω) = (exp

¯hω

− 1)

−1

Тогда

= 3R

¯hω

exp

−

¯hω

exp

−

¯hω

− 1

(3.22)

Таким образом, удельная теплоемкость равняется 3R при высоких температурах и

экспоненциально мала при низких T . Экспериментальные данные демонстрируют

более медленное уменьшение удельной теплоемкости. Это происходит из-за того,

что модель Эйнштейна хорошо подходит только для оптических ветвей решеточных

колебаний (фононов), частоты которых слабо зависят от волнового вектора. Вычис-

ление акустического вклада ветви с модельным дисперсионным законом

= sq (q < q

), ω

= sq

= k

/¯h (3.23)

было выполнено Дебаем. Результат имеет вид

= 3R

− 1)

(3.24)

При высоких T мы снова приходим к закону Дюлонга и Пти. При низких T ¿ θ

удельная теплоемкость удовлетворяет дебаевскому закону T

= 12

(3.25)

Более точное вычисление фононного вклада в удельную теплоемкость в широкой

температурной области требует использования более реалистического закона дис-

персии фононов, который может быть очень сложным. Например, эксперименталь-

ные данные для акустических ветвей для Nb и Mo показываются на Рис. 3.17. Можно

видеть, что зависимость ω(q) для Mo оказывается немонотонной. Аномалии в кри-

вых ω(q) связаны с сильным электрон-фононным взаимодействием в переходных

металлах.

Данные по удельной теплоемкости простых и переходных металлов в широкой

температурной области представлены в справочнике [239], где обсуждаются зако-

номерности в поведении c(T ) для различных столбцов периодической таблицы. За-

висимости c( T ) в пределах одного столбца оказывается подобными и отличаются

главным образом особенностями вследствие структурных и магнитных переходов.

Например, теплоемкость ванадия (в котором нет таких фазовых переходов) показа-

на на Рис. 3.18; здесь зависимость c(T ) имеет простую форму. Можно видеть, что

закон Дюлонга и Пти справедлив в не слишком широкой температурной области и

нарушается как при низких, так и при высоких T . Более сложное поведение имеет

место для Zr (Рис. 3.19), где присутствует структурное α − β превращение, и в тя-

желых редкоземельных элементах (Рис. 3.20), которые имеют сложную магнитную

диаграмму состояния.

Скачок удельной теплоемкости в точке плавления, ∆c

= c(T > T

) −c(T < T

)

является как правило положительным для переходных металлов, которые имеют

фазовые переходы (включая легкие редкоземельные элементы, Fe, Co, Ni) и отри-

цательным для металлов, у которых фазовые переходы не наблюдаются (например,

для Nb, Ta, хотя малый положительный ∆c

наблюдается для ванадия). Нужно от-

метить, что ситуация для простых металлов отличается: ∆c

> 0 для Zn, Cd, Al,

Ga, In, Pb, несмотря на отсутствие структурных фазовых переходов.

В жидкой фазе удельная теплоемкость d-металлов может достигать значений 4-

9R, что значительно больше, чем для простых металлов (см., например, обсуждение

в [258]).

Увеличение c по сравнению с 3R, наблюдаемое выше комнатной температуры в

большинстве веществ, обычно приписывается ангармоническим эффектам, которые

приводят к линейным по T членам в высокотемпературной решеточной теплоемко-

сти. Мы проиллюстрируем это явление в простой одномерной модели с потенциалом

(3.10)(более детальное обсуждение дается в [4]). Запишем статистическую сумму для

иона в виде

Z(T ) =

dpdu exp

[−

+ V (u)]/k

(3.26)

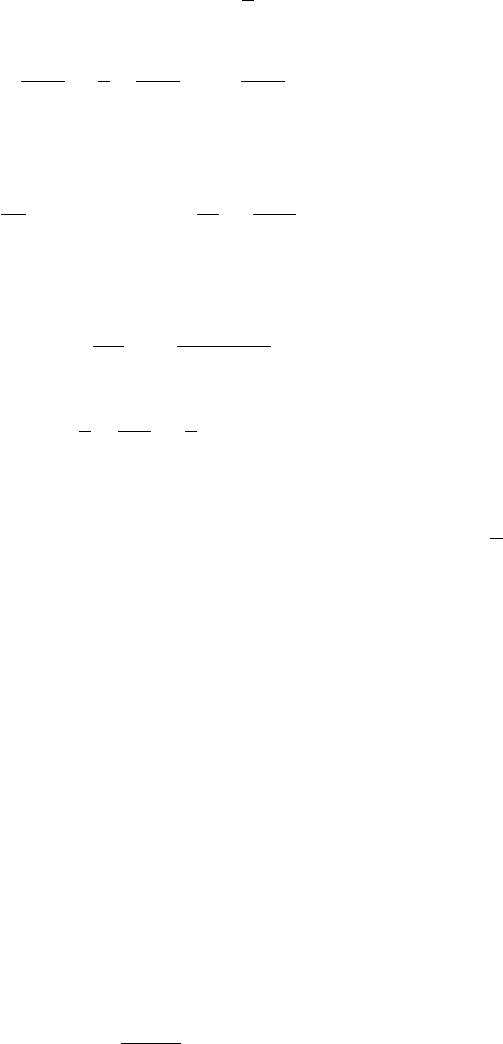
Интегрируя по импульсу p и разлагая по параметрам ангармонизма до b

и c, мы

получаем

Z(T ) = (2πk

T M)

1/2

du exp

−

1 +

(3.27)

Интегрирование по u дает

Z(T ) = 2π

1/2

1 −

−

15b

(3.28)

Тогда удельная теплоемкость определяется выражением

c(T ) = −3N

∂

∂T

∂ ln Z(T )

∂T

= 3R

1 +

−

(3.29)

Так как a/b ∼ b/c ∼ d и среднее смещение дается выражением (3.11), линейные по

T поправки, обусловленные ангармоническими членами третьего и четвертого по-

рядка, имеют одинаковый порядок величины и могут быть оценены как (u/d)3R.

Поэтому ангармонизм едва ли способен объяснить увеличение удельной теплоемко-

сти при высоких температурах в d-металлах, которое может быть порядка 100%, так

что эта проблема нуждается в дальнейших исследованиях.

3.3.2 Электронная удельная теплоемкость

Помимо нарушения закона Дюлонга и Пти при низких температурах, вторая труд-

ность классической теории удельной теплоемкости касается электронного вклада в

теплоемкость. Согласно (3.20), этот вклад должен быть равен 3R/2 для металла

с одним электроном на атом. Однако такие большие вклады никогда не были об-

наружены в эксперименте (в теплоемкости наблюдается только малый линейный

электронный член).

Это противоречие было разрешено только в двадцатых годах ХХ столетия после

формулировки статистики Ферми-Дирака для электронов. Соответствующая функ-

ция распределения имеет вид

f(E) = (exp

E − ζ

+ 1)

−1

(3.30)

где ζ = ζ(T ) - химический потенциал, ζ(0) равно максимальной энергии занятых со-

стояний - энергии Ферми E

. Последняя величина определяется, согласно принципу

Паули, числом электронов:

n =

∞

−∞

dEf(E)N(E) (3.31)

(в этом разделе плотность состояний N(E) определена для обеих проекций спина).

В металлах E

велико и составляет около 10

-10

K. Это качественно объясняет

малое значение электронной теплоемкости. Действительно, только электроны в уз-

ком слое с шириной около πk

T около уровня Ферми могут изменять свою энергию

и принимать участие в тепловых возбуждениях, а большинство электронов заморо-

жено. Число “тепловых"электронов оценивается как

∗

/n ∼ k

T N(E

) ∼ k

T/E

(3.32)

так что

δE

(T ) ∼

∗

T ∼ k

N(E

) (3.33)

∼ k

N(E

Более точное вычисление (см. ниже (3.40)) дает

= γT, γ =

N(E

) (3.34)

Таким образом, электронная удельная теплоемкость должна быть линейной в широ-

ком температурном интервале 0 < T < E/k

(фактически, до температур, которые

превышают температуру плавления). Электронный вклад может быть обнаружен

при низких T , где вклад решетки быстро уменьшается. С этой целью мы можем

записать

/T = γ + αT

(3.35)

и экстраполировать экспериментальную зависимость c

/T вместо T

при нулевой

температуре.

Согласно (3.34), значение γ определяется наиболее важной характеристикой элек-

тронной системы в металле - плотностью состояний на уровне Ферми. Так как пере-

ходные металлы характеризуются большими значениями N(E

), соответствующие

им величины γ (Таблица 3.5) значительно больше, чем для простых металлов. Осо-

бенно большие значения наблюдаются в d-соединениях с пиками N(E) на уровне

Ферми. Сюда относятся сверхпроводники со структурой A-15 (например, γ = 33

мДж/моль K

для V

Ga, см. также Рис. 6.1).

Экспериментальные значения γ можно сравнить с результатами расчетов зонной

структуры по формуле

γ (mJ/molK

) = 0.1734 · N(E

) (states/Ry)

Как можно видеть из Таблицы 3.5, имеет место явная корреляция между этими зна-

чениями. Так же как N(E

), γ

exp

как функция числа d-электронов демонстрирует

“зубчатое "поведение - большие значения для конфигураций d

с нечетным n и ма-

лые значения для четных n (отношение γ

exp

/γ

theor

не показывает такого поведения).

В середине d-ряда γ

exp

/γ

theor

несколько меньше, чем в начале или в конце.

Теоретические значения γ оказываются как правило меньше, чем эксперимен-

тальные. Эта разность является большой для переходных элементов. Так, для Sc,

Ti, V, Y, Zr, Nb, Hf, Ta имеем γ

exp

/γ

theor

∼ 2, а для соседних простых металлов

Ca, Ba, Cu, Ag, Au это отношение близко к единице. Таким образом, отклонение

может быть частично приписано эффектам корреляции, которые являются более

важными в переходных металлах. В этой связи мы упомянем вычисление зонной

структуры из первых принципов без использования метода функционала плотности

[259], где получено значительное изменение значения N(E

) и улучшение согласия

с экспериментальными данными для величины γ.

Кроме того, нужно иметь в виду погрешность в расчетах зонной структуры. Так

как плотность состояний в ПM имеет резкую энергетическую зависимость, малые

ошибки в положении уровня Ферми могут сильно повлиять на значение N(E

). Соот-

ношение γ

exp

< γ

theor

для хрома вероятно связано с влиянием антиферромагнитного

упорядочивания, которое не учитывается в расчетах зонной структуры, но может

значительно нарушить электронную структуру вблизи уровня Ферми (формирова-

ние антиферромагнитной щели).

Увеличение γ

exp

по сравнению с γ

theor

можно объяснять эффектами взаимодей-

ствия электронов проводимости с различными элементарными возбуждениями в

кристалле. Очень часто считают, что электрон-фононное взаимодействие приводит

к появлению множителя 1 + λ в электронной эффективной массе, и, следовательно,

. Теоретическое вычисление

- очень трудная задача, так как оно требует деталь-

ной информации относительно характеристик электронных и фононных подсистем.

В переходных металлах электрон-фононное взаимодействие велико из-за сильной за-

висимости полной энергии от параметра решетки. Большое значение λ ведет также

к сверхпроводимости с довольно высокой T

[257]. Следует отметить, что λ при этом

будет иметь заметную температурную зависимость. Вычисления этой зависимости

выполнено как в модели Эйнштейна, так и в модели Дебая в работах [260] и [261]

соответственно. Результаты [261] показаны на Рис. 3.21. Можно видеть, что λ(T )

быстро уменьшается при T > 0.2θ

Другой важный механизм усиления удельной теплоемкости - взаимодействие со

спиновыми флуктуациями. Этот механизм, который является особенно важным для

слабых магнетиков и почти магнитных переходных металлов и их соединений (на-

пример, γ = 56 мДж/моль K

для почти антиферромагнитной системы TiBe

[507]),

обсуждается в Разд. 4.4 и в Приложении G.

Интересный пример представляет металлический празеодим, где взаимодействие

с возбуждениями в кристаллическом электрическом поле, как предполагается, обес-

печивает усиление m

∗

/m ' 4 [263]. Подобные эффекты спиновых и зарядовых флук-

туаций в аномальных редких землях и системах с актинидами рассматриваются в

Разд. 6.3.

Температурная зависимость электронной удельной теплоемкости в переходных

металлах оказывается достаточно сильной. Соответствующие экспериментальные

результаты показаны на Рис. 3.22. Нужно отметить, что определение электронного

вклада на фоне решеточного было выполнено в [262] в рамках дебаевского прибли-

жения. Последнее не вполне удовлетворительно при высоких T , где c

составляет

приблизительно 10% от полной удельной теплоемкости.

Наиболее простая причина зависимости γ(T ) - размытие функции Ферми с тем-

пературой. Чтобы рассмотреть этот эффект, мы рассмотрим выражения для числа

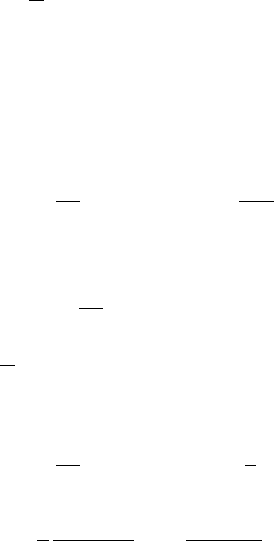
частиц (3.31) и средней энергии

∞

−∞

EdEf(E)N(E) (3.36)

Далее мы используем разложение интегралов Зоммерфельда

∞

−∞

dEf(E)F (E)

−∞

dEF (E) +

T )

(ζ) +

7π

360

T )

(ζ) + ... (3.37)

которое получается с использованием интегрирования по частям. Тогда мы имеем

ζ(T ) = E

−

T )

)/N(E

) + ... (3.38)

N(E

)

−∞

dEN(E) + γ(T )T (3.39)

где

γ(T ) =

N(E

)

1 +

(πk

T )

)

N(E

)

−

)

N(E

)

(3.40)

Температурные поправки, хотя и являются формально малыми, особенно важны

в случае сильной зависимости N(E), которая является типичной для переходных

металлов. Первый член в квадратных скобках означает, что удельная теплоемкость

при конечных T определяется плотностью состояний, усредненной по энергетическо-

му интервалу порядка πk

T вблизи E

. В частности, при N

) = 0, N

) > 0

(минимум функции N(E)) γ возрастает с T , а при N

(E) < 0 убывает с T . Этот

результат качественно согласуется с результатами вычислений зонной структуры и

экспериментальными данными относительно знака T -зависимости (Рис. 3.22): для

нечетных d

конфигураций (V, Ta, Nb, Pt, Pd) большие значения γ, которых соот-

ветствуют максимуму N(E),и убывают с T , а для четных конфигураций (Zr, Ti, Cr,

Mo, W) малые значения γ соответствуют минимуму N(E) и возрастают с T . Вто-

рой член в квадратных скобках (3.40) появляется из-за температурной зависимости

химического потенциала (3.38).

Шимицу [262] выполнил численные расчеты, чтобы сравнить эксперименталь-

ные зависимости γ(T ) со следующими из первопринципных (Рис. 3.23) и эмпири-

ческих (Рис. 3.24) плотностей состояний. Хотя имеет место качественное согласие,

теоретические зависимости оказываются более слабыми и сдвинутыми к высоким

температурам.

При условии, что функция N(E) обладает сингулярным поведением около E

(узкие пики), разложение (3.37) несправедливо и необходимо более сложное анали-

тическое вычисление. Расчет зависимости γ(T ) в присутствии пиков ПС выполнен

в [264]. Использовалась простая модель N(E) с треугольными пиками при E = E

δN(E) =

δN

(E) (3.41)

δN(E) =

(E − E

) , E < E

− E) , E > E

Относительное изменение с температурой равно

γ(T ) =

− I

) (3.42)

где

∞

−∞

−

∂f(E)

∂E

(E − E

)

N(E) (3.43)

В отличие от выражения (3.40), оно может быть большим. Используя положения

пиков E

и скачков N

(E) в этих точках как параметры, плотность состояний можно

восстановить по экспериментальной зависимости γ и сравнить ее с расчетной. Такой

анализ был выполнен в [264] для сверхпроводников со структурой A-15 Nb

Sn и V

Si.

Помимо одноэлектронного механизма, зависимость γ(T ) определяется обсужден-

ными выше температурными зависимостями электрон-фононного усиления и кор-

реляционных механизмов, которые, как ожидается, будут довольно сильными для

d-зон. Относительная роль этих эффектов для переходных металлов в деталях пока

не исследована.

3.3.3 Удельная теплоемкость магнитных металлов

В магнитоупорядоченных кристаллах появляются вклады в энтропию и теплоем-

кость, которые обусловлены разрушением магнитного порядка с увеличением тем-

пературы. Экспериментальное разделение магнитной энтропии может быть выпол-

нено с использованием магнитокалорического эффекта (изменение температуры при

адиабатическом намагничивании внешним магнитным полем) [265].

В модели локализованных спинов с величиной S полное изменение магнитной

энтропии имеет вид

mag

(T → ∞) =

∞

mag

(T ) = R ln(2S + 1) (3.44)

Магнитная теплоемкость c

mag

особенно важна в точках магнитных фазовых перехо-

дов T

= T

), где она имеет особенность. В простейшем приближении среднего

поля c

mag

экспоненциально мала при низких температурах, испытывает скачок при

пересечении T

и исчезает в парамагнитной области, так, что выражение (3.44)

справедливо для произвольной T > T

. Фактически, наличие ближнего порядка,

которым пренебрегают в теориях среднего поля, приводит к конечности c

mag

вы-

ше T

из-за взаимодействия со спиновыми флуктуациями. Кроме того, флуктуа-

ции приводят к слабой степенной расходимости c

mag

при T

. Экспериментальные

температурные зависимости удельной теплоемкости в ферромагнитных переходных

металлах показаны на Рис.3.25, 3.26.

При низких температурах (значительно ниже T

) существуют вклады от спи-

новых волн (магнонов) (Приложение E). Соответствующая средняя энергия имеет

вид

(T ) =

¯hω

(3.45)

где ω

- частота магнона. Так как в ферромагнетиках ω

∼ q

at q → 0, мы имеем

(T ) ∼ T

5/2

3/2

, c

∼ (T/T

)

3/2

(3.46)

В то же время, для антиферромагнетиков дисперсионный закон линеен, и мы полу-

чаем

(T ) ∼ T

, c

∼ (T/T

)

(3.47)

Вклады от спиновых волн присутствуют как в магнитных изоляторах, так и в метал-

лах. В металлах линейная электронная удельная теплоемкость доминирует при низ-

ких температурах, а спин-волновые поправки менее важны. Однако на электронный

вклад заметно влияет магнитный порядок. Так как усиление линейного γT -члена

происходит из-за взаимодействия со спиновыми флуктуациями (Разд. 4.4), строгое

разделение магнитного и электронного вкладов, вообще говоря, невозможно. Некото-

рые специфические члены в удельной теплоемкости ферромагнитных проводников,

которые появляются из-за некогерентных (неквазичастичных) вкладов, обсуждают-

ся в Приложении G.

Электронная плотность состояний в упорядоченной фазе ферромагнитных ме-

таллов (ниже точки Кюри T

) значительно отличается от плотности в парамагнит-

ной фазе из-за спинового расщепления. Как правило, полная N(E

) = N

↑

) +

↓

) меньше в ферромагнитном состоянии, так что упорядочение приводит к

сдвигу пика, который является ответственным за стонеровскую неустойчивость, с

уровня Ферми. В то же время, в никеле значение γ(T < T

) = 7.0 мДж/моль K

[266] больше, чем γ(T > T

) = 5.8 мДж/моль K

[267]. Это ведет к заключению

относительно важной роли эффектов корреляции.

Рассмотрим простейшую теорию магнитной теплоемкости. В приближении сред-

него поля магнитная (обменная) энергия записывается через намагниченность:

mag

= −IM

(3.48)

где I - обменный параметр. Тогда магнитная теплоемкость имеет вид

mag

= −IM

(3.49)

В металлах помимо обменной энергии нужно принять во внимание кинетическую

энергию электронов проводимости, которая зависит от намагниченности через об-

менное расщепление. Полная энергия в модели Стонера (см. Разд. 4.3) может быть

преобразована следующим образом

E =

kσ

+ In

↓

kσ

− In

↓

dEEf(E)N

(E) − I

− M

(3.50)

где

+ σM, E

kσ

= E

− σIM

(E) =

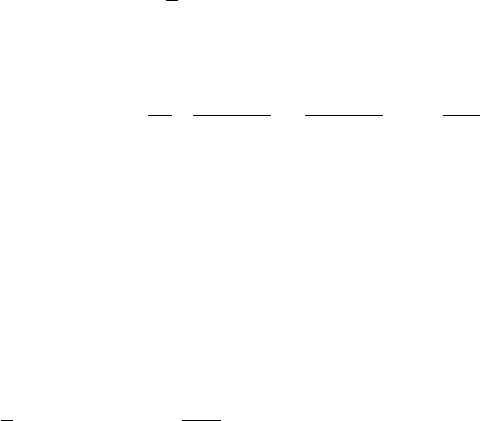
N(E + σIM) (3.51)

Дифференцируя по T , легко получить

c(T ) = c

↓

(T ) + c

↓

(T ) +

↑

)

↑

)

−

↓

)

↓

)

(3.52)

где c

(T ) - обычная электронная удельная теплоемкость, соответствующая плотно-

сти состояний N

(E). Можно видеть, что член типа (3.49) сокращается с соответ-

ствующим вкладом от кинетической энергии. Магнитная теплоемкость определяется

вторым членом в (3.52). Вклад в c

mag

вносят только электроны в энергетическом слое

порядка T вблизи уровня Ферми, так что она содержит малый множитель порядка

T/E

)

и сильно зависит от формы ПС. Скачок удельной теплоемкости в точке

Кюри имеет вид [26]

∆c =

(πT

)

{[N

)

∂ζ

∂M

+ I

)]}

T =T

(3.53)

Ситуация может несколько измениться в присутствии пиков плотности состояний.

Рассмотрение удельной теплоемкости Ni с учетом реалистической структуры ПС вы-

полнено в [268]. Так же как в гейзенберговских магнетиках, спиновые флуктуации

приводят к значительной модификации поведения c

mag

(T ) при высоких температу-

рах [26,268].

Ирхин В.Ю., Ирхин Ю.П. Электронная структура, корреляционные эффекты и физические свойства d - и f-переходных металлов и их соединений

Подождите немного. Документ загружается.