Ипатов В.П. Широкополосные сигналы

Подождите немного. Документ загружается.

рис. 2.5, а. Тогда угол между векторами

составит величину



, а

1cos



и, значит,

Ed 2),(

ss

, что преобразует соотношение (2.18) в следую-

щее















, (2.19)

обеспечивающее минимально достижимую вероятность ошибки при передаче двоичных

данных сигналами с фиксированной энергией

. Такие устройства, как коррелятор (cor-

relator) и согласованный фильтр (matched filter), которые часто упоминаются в дальней-

шем, используются для непосредственного вычисления корреляции

, а параметр

/2 NEq 

есть ничто иное, как отношение сигнал-шум (signal-to-noise (SNR)) на выхо-

де упомянутых устройств.

Таким образом, оптимальной сигнальной парой служат противоположные сигналы

вида

)()(

tsts 

. Бинарная фазовая манипуляция (binary phase shift keying (BPSK)) пред-

ставляет собой их практическую реализацию, широко используемую в цифровых систе-

мах передачи данных. При этом нулевой символ данных передается радиосигналом с на-

чальной фазой, равно нулю, а тот же самый сигнал, но с начальной фазой высокочастот-

ного заполнения, равной



, используется для передачи единицы.

Для определения критичности в выборе сигнальной пары сравним BPSK с другим

популярным методом передачи двоичных данных. Хотя BPSK является наилучшим из

возможных способов передачи двоичной информации, его применение основано на фазо-

вом различии двух сигналов, носителей информации, и, следовательно, требует точного

знания на приемной стороне текущего значения фазы несущей частоты. Практическая

реализация этого достигается путем применения специального устройства восстановления

несущей, что иногда рассматривается, как нежелательное усложнение приемной схемы.

Избежать подобного усложнения удается при использовании другого способа манипуля-

ции – частотной (frequency shift keying (FSK)), при которой сообщения 0 и 1 передаются

сигналами на различных частотах. Типичным является такой выбор несущих частот, при

котором сигналы оказываются ортогональными (orthogonal), т.е.

0cos



Ed 2),(

ss

(см. рис. 2.5, b). Подстановка этих значений в (2.18) дает















. (2.20)

Сравнение результатов (2.20) и (2.19) демонстрирует, что для ортогональной пары (FSK)

обеспечение вероятности ошибочного приема, аналогичной случаю использования проти-

= – s

Рис. 2.5. Варианты выбора пар двоичных сигналов.

воположных сигналов (BPSK), достигается только при двукратном увеличении энергии

сигналов. Иными словами, ортогональные сигналы проигрывают 3 дБ противоположным

в уровне необходимой энергии.

Существует еще один, достаточно старый, способ передачи двоичной информации,

до сих пор использующийся на практике: амплитудная модуляция (amplitude shift keying

(ASK)), при которой символ данных «1» передается сигналом

)()(

tsts 

с энергией

EE 

, а символ «0» – паузой, т.е.

0,0)(

 Ets

. В этом случае (см. рис. 2.5, с)

Ed ),(

, а вероятность ошибки (2.18) становится равной















ase

. (2.21)

Сравнивая последний результат с (2.19), можно сделать вывод о том, что ASK требует в 4

раза (6 дБ) большей энергии, чем в случае BPSK, для обеспечения одинаковой достовер-

ности приема. Последнее утверждение справедливо тогда, когда накладывается ограниче-

ние на пиковую энергию. На практике, как правило, ограничение накладывается на сред-

нюю энергию. А поскольку при ASK энергия не излучается при передаче нулевых симво-

лов, то при равновероятных сообщениях «0» и «1» средняя энергия определится, как

2/2/)(

EEE 

. Тогда при условии одинаковой вероятности ошибки ASK проигрывает

BPSK в средней энергии только в два раза. Значит, для ASK по отношению к BPSK харак-

терны такие же энергетические потери, как и в случае применения FSK, т.е. 3 дБ.

На основании предыдущих рассуждений можно сделать следующий вывод о задаче

выбора пары сигналов для передачи двоичной информации: отсутствуют малейшие на-

меки на получение каких-либо преимуществ при использовании сигналов с распределенным

спектром, поскольку расширение полосы сигнала сверх ее минимума

T/1

не приведет к

уменьшению вероятности ошибки. Действительно, для обеспечения желаемой достовер-

ности приема достаточно только применить пару сигналов, максимально удаленных друг

от друга, что автоматически предполагает использование противоположных сигналов без

дополнительных требований к их форме и модуляции. Если по каким-либо причинам ис-

пользование пары противоположных сигналов отвергается, то альтернативный вариант

выбора сигналов – ортогональная, иначе частотно–модулированная, или амплитудно–

модулированная пара сигналов также не предполагает применение технологии распреде-

ленного спектра.

2.3. Передача М–ичных данных (детерминированные сигналы).

При возможном числе сигналов

2M

вероятность

перепутывания действи-

тельно принятого

)(

с одним из

1M

ошибочных сигналов

Mjts

,,3,2),( 

, опре-

деляется, согласно решающим правилам (2.3) и (2.8), как

))()

(max

(1))(),(min),((

zPtsddPp

 ysys

Определение точной оценки этой вероятности состоит в интегрировании условной обоб-

щенной плотности вероятности всех

корреляций при условии истинности принятия

сигнала

)(

по всей области выполнения неравенства





Mi ,,2,1 

Этот

– кратный интеграл в общем случае, т.е. в отсутствии предположений о свойствах

множества сигналов, никаким образом не может быть упрощен. Однако очень продуктив-

ная и точная верхняя граница для вероятности

может быть получена на основании

аддитивной (union) границы. Пусть событие

состоит в том, что наблюдение

)(ty

ока-

зывается наиболее близким не к

)(

, а к некоторому другому сигналу

Mjts

,,3,2),( 

. Тогда событие, заключающееся в перепутывании сигнала

)(

с не-

которым другим сигналом, войдет в объединение всех

. Согласно аддитивной границы

вероятность объединения событий никогда не может быть больше суммы их вероятно-

стей, т.е.







jMe

APAAAPp

32,1

)()( 

С другой стороны, вероятность

)(

, как следует из определения события

, в

точности совпадает с вероятностью перепутывания только между двумя сигналами

)(

)(ts

. Значение этой вероятности определяется соотношением (2.17) после соответст-

вующей замены номеров сигналов:















),(

)(

QpAP

Подстановка последнего соотношения в ранее приведенное неравенство приводит к же-

лаемой оценке



















),( ss

Аналогичный результат (с необходимой подстановкой новых числовых индексов)

будет получен и в предположении, что вместо

)(

фактически принятым считается сиг-

нал

)(ts

, так что, с учетом а приори равной вероятности

сигналов, окончательная ад-

дитивная верхняя граница для полной (безусловной) вероятности ошибки примет вид

  

 























eie

1 1

),(

. (2.22)

Первым заслуживающим внимание фактом, который непосредственно следует из

(2.22), является то, что при

2M

данное неравенство превращается в равенство. Другое

замечание связано с поведением (2.22) в асимптотике при росте отношения сигнал-шум. В

самом деле, дополнительная функция ошибки

)(xQ

уменьшается как

)2/exp(

x

при

достаточно большом

и даже незначительное его увеличение может уменьшить

)(xQ

до

пренебрежимо малого уровня по сравнению с начальным значением. Вследствие этого

при достаточно большом отношении сигнал-шум только близко расположенные сигналь-

ные пары могут вносить заметный вклад в значение суммы в (2.22), и если

min

есть ми-

нимальное расстояние на множестве всех возможных пар, встречающееся

min

раз, то

оценка (2.22) в асимптотическом случае трансформируется к виду

min

minmin

















. (2.23)

Приближение (2.23) указывает, прежде всего, на асимптотическую сходимость ад-

дитивной границы с истинным значением вероятности ошибки при увеличении отноше-

ния сигнал-шум. Для физического объяснения данного факта обратимся вновь к рис. 2.3 и

отметим, что при малом уровне шума только те сигнальные вектора, которые расположе-

ны вблизи от истинного, могут быть ошибочно приняты за искомый. Это означает, что

асимптотически только сигнальные пары с расстоянием

min

определяют истинное зна-

чение вероятности ошибки

(а не только ее верхней границы), что влечет за собой бли-

зость величины

и ее аддитивной границы.

Соотношение (2.23) содержит одну из возможных и наиболее важных формулиро-

вок задачи конструирования сигналов: максимизацию минимума расстояния между

сигналами. Как уже упоминалось в 2.1, подобная задача в геометрической интерпретации

эквивалентна упаковке

векторов таким образом, чтобы ближайшая их пара находилась

на максимально достижимом расстоянии, т.е.

max

min

d

. На созвездие сигналов (векто-

ров) могут быть наложены различные ограничения. Прежде всего, следует предусмотреть

определенные энергетические ограничения, учитывая практические мощностно–

энергетические ресурсы. Если фиксировать только среднюю энергию сигналов

constMEE





1

, то сигнальные вектора могут иметь различную длину и процедуру

выбора сигналов можно назвать объемной упаковкой (volume packing). Тем не менее, часто

при решении задачи отображения сообщений в сигналы выдвигается требование исклю-

чения влияния энергетического параметра, т.е. требование одинаковой

constEE



Mi ,,2,1 

энергии всех сигналов. В этом случае все сигнальные вектора имеют одина-

ковую длину, и значит, лежат на сферической поверхности, откуда и следует название за-

дачи – сферическая упаковка (spherical packing).

Другим типичным ограничением при синтезе сигналов является размерность

сигнального пространства, внутри которого и осуществляется их упаковка. Физическая

сущность этого ограничения снова обусловлена практическим ресурсом, но теперь шири-

ной частотной полосы. Для объяснения существующей связи рассмотрим первоначально

видеосигналы и предположим, что общий (двумерный) частотно–временной ресурс, в ко-

тором могут располагаться все

сигналов, ограничен параметрами

соответст-

венно. Первое из этих ограничений учитывает экономию полосы, тогда как второе отра-

жает желание передавать данные с приемлемой скоростью

TMR /log

. Тогда, согласно

теореме отсчетов, имеется около

независимых отсчетов, которые могут быть исполь-

зованы при синтезе

сигналов, причем каждый из сигналов трактуется как вектор в

пространстве размерности

tts

TWn 

. Определенная осторожность в оценке числа незави-

симых отсчетов объясняется невозможностью концентрации энергии любого сигнала в

пределах конечного и во времени и по частоте интервала. Однако в первом приближении

этим фактом можно пренебречь.

Для того чтобы охватить и случай полосных (радио) сигналов обратимся к общей

модели подобного сигнала

)](2cos[)()(

ttftSts 

, (2.24)

где

)(tS

– вещественная огибающая сигнала, отражающая закон модуляции амплитуды,

)(t

описывает закон фазовой модуляции, а

– несущая частота. Используя тригоно-

метрическое преобразование для косинуса суммы углов, (2.24) можно представить в виде

tfStftSts

QI 00

2sin2cos)()( 

, (2.25)

где

)(cos)()( ttStS



, а

)(sin)()( ttStS



– квадратурные компоненты (quadrature

components) сигнала. Поскольку и

)(tS

, и

)(t

являются видеосигналами, то данное ут-

верждение справедливо и в отношении

)(),( tStS

. Последнее означает, что при перено-

се на несущую частоту любой радиосигнал исчерпывающе описывается двумя независи-

мыми низкочастотными квадратурными компонентами. Следовательно, при синтезе по-

лосных сигналов могут использоваться в два раза больше независимых координат (отсче-

тов), чем в случае видеосигналов при одинаковых значениях частотно-временного произ-

ведения и, значит,

tts

TWn 2

Теперь в общем виде задача выбора множества сигналов может быть сформулиро-

вана следующим образом: найти в пространстве заданной размерности

созвездие из

точек или векторов, удовлетворяющее энергетическим ограничениям и обладающее мак-

симально возможным минимумом расстояния между точками

max

min

d

. Данная задача

может быть переформулирована в дуальную: найти в пространстве заданной размерности

созвездие из

точек или векторов с гарантированным минимальным расстоянием

min

, которое обеспечивает минимизацию энергетических затрат, либо в терминах сред-

ней энергии

minE

(объемная упаковка), или просто

minE

(сферическая упаковка).

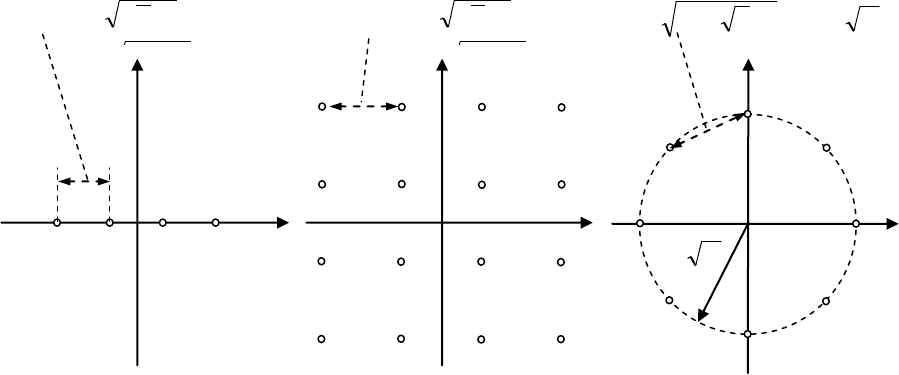
Простейшая версия этой задачи (

1

) отвечает случаю амплитудной (ASK) мо-

дуляции (простейший вариант которой с

2M

– бинарная модуляция – был упомянут в

2.2). Альтернативным наименованием ASK служит импульсно–кодовая модуляция (pulse

amplitude modulation (PAM)). В этом случае все сигнальные точки располагаются на одной

прямой линии, и при

2M

речь может идти только о задаче «объемной» упаковки. Не

составляет труда убедиться, что при заданном

min

оптимальное созвездие, минимизи-

рующее среднюю энергию, образуется в результате равномерного и симметричного рас-

положения сигнальных точек с пространственным разнесением соседних на величину, в

точности равной

min

(см. рис. 2.6, а).

При

2

задача нахождения оптимального созвездия с объемной упаковкой ста-

новится более трудной и может даже привести к ассиметричным моделям, тогда как сфе-

рическая упаковка осуществляется тривиальным образом и реализуется равномерным

размещением

точек по окружности радиуса

. Широко используемая в современной

цифровой связи

–ичная квадратурная амплитудная модуляция (quadrature amplitude

modulation (QAM)) служит примером двумерного, симметричного объемно-упакованного

созвездия, которое, не являясь оптимальным теоретически, практично с точки зрения ап-

паратной реализации (Рис. 2.6, b). С другой стороны, обычные

–ичные фазоманипули-

рованные (phase shift keying (PSK)) созвездия образованы равномерно расположенными на

окружностями точками и оптимальны с точки зрения сферической упаковки (Рис. 2.6, c).

Задача оптимального расположения точек в пространстве большей размерности

)2( 

является чрезвычайно сложной и не имеет до сих пор общего математического

решения. Много полезных, но частных результатов содержится в целом ряде книг и статей

(см., например, библиографию в [11] и веб-сайт [12]).

Попытаемся теперь определить верхний предел минимума расстояния в отсутствии

предварительного ограничения на размерность сигнального пространства

, а также ми-

нимальное значение

, которое позволит обеспечить найденный предел. Ограничиваясь

только случаем сферической упаковки

),,2,1,( MiEE



, вычислим сумму всех

возможных квадратов расстояний, включая и тривиальные (т.е. расстояния для любых

сигналов с самим собой). Тогда на основании теоремы косинусов (2.16) получаем







EEMd

22),( ss

, (2.26)

где



– коэффициент корреляции между

–м и

– сигналами. Для оценки суммы всех

коэффициентов корреляции воспользуемся определением (2.14) для



, поменяем поря-

док интегрирования и суммирования и отметим, что двойное суммирование под знаком

интеграла осуществляется по раздельным индексам

, а значит, его можно заменить

произведением двух идентичных сумм:

 

































T T

dttsdttstsE

0 0

11,1,

)()()(

Поскольку интеграл от квадрата подынтегрального выражения никогда не будет отрица-

тельным, из (2.26) вытекает, что







EMd

2),( ss

В то же время приведенная выше сумма не меньше, чем

min

)1( dMM 

. Учитывая оба

указанных неравенства, можно получить следующую верхнюю границу для минимума

расстояния

5/4

min

Ed 

5/4

min

Ed 

5/2

min

Ed 

5/4

min

Ed 

EEd 77.0)22(

min



5/4

min

Ed 

Рис. 2.6. Одно- и двумерные созвездия: 4-ASK (a), 16-QAM (b), и 8-PSK (c).

min





. (2.27)

Если существуют

сигналов, достигающие этой верхней границы, то совершенно

справедливо будет назвать их оптимальными по критерию минимума расстояния. Для до-

казательства существования подобного множества сигналов рассмотрим

векторов

,,2,1, u

, имеющих попарно нулевое скалярное произведение и единичную длину:

Mji

ijji

,,2,1,,),( uu

, где

jiji

ijij

 ,1;,0

– дельта-функция Кронекера.

Такие вектора, называемые ортонормированными (orthonormal), существуют в любом

векторном пространстве, размерность которого не меньше, чем

. Сформируем теперь

новых векторов

,,2,1, v

, каждый из которых образован в виде разности век-

торов

и их суммы





, взвешенной коэффициентом

M/1

, т.е.

/uuv 

Учитывая свойство линейности, скалярное произведение векторов

определится

как

ijjijiji

),(

),(),(

 uuuuuuuuvv

, (2.28)

где при вычислении принята во внимание ортогональность векторов

. Изменим теперь

длину векторов

путем умножения их на

)1/( MME

и используем полученные векто-

ра в качестве сигнальных:

,,2,1,





 vs

. (2.29)

Тогда, согласно теореме косинусов (2.16) и соотношению (2.29), квадрат расстояния меж-

ду двумя сигналами будет

jijijiji



























 ,

),(2

),(

vvvvvvss

, (2.30)

что совпадает с правой частью соотношения (2.27). Следовательно, сигналы, удовлетво-

ряющие границе (2.27) действительно существуют. Более того, расстояние между любой

их парой также определяется этой величиной, поэтому приведенные сигналы попадают в

категорию эквидистантных (equidistant). Данный класс сигналов широко известен под

специальным наименованием симплексных (simplex) сигналов. Непосредственно из их оп-

ределения вытекает, что

0)()1/()1/(







uuvs MMEMME

означающее, что в отличие от исходных ортогональных векторов

симплексные сигна-

лы линейно зависимы. Легко убедиться, что размерность пространства

1 Mn

, т.е. на

единицу меньше числа сигналов, необходима и достаточна для построения

симплекс-

ных сигналов.

Свойство эквидистантности симплексных сигналов влечет за собой равенство ко-

эффициентов корреляции



любой их пары. Оценка величины



с помощью (2.14),

(2.29) и (2.28) приводит к следующему результату

Mjiji

,,2,1,,,

),(







демонстрирующему, что угол между любыми двумя симплексными сигналами один и тот

же и больше, чем

2/

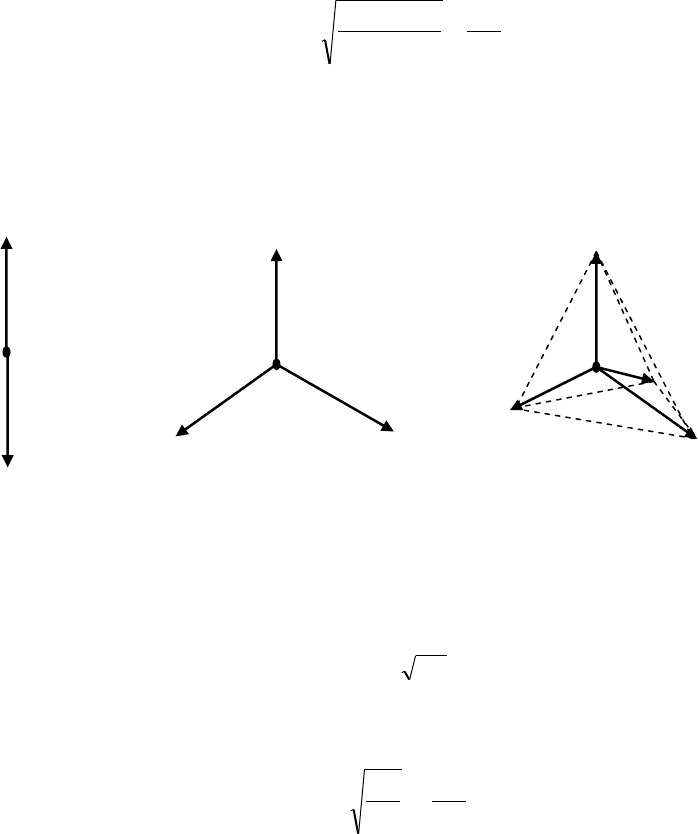
. Для простейших множеств из

4,3,2M

симплексных сигналов,

представленных на рис. 2.7, величина коэффициента корреляции принимает значения,

равные –1 (противоположные сигналы), –1/2 и –1/3 соответственно, что в свою очередь

отвечает углам в 180, 120 и примерно 110. При

4M

симплексные вектора образуют

простейший правильный многогранник (тетраэдр), что объясняет наименование сигналов:

«симплекс» на латинском означает «простой».

В любом множестве эквидистантных сигналов

min

),( dd

ss

для любой пары

различных векторов, так что в (2.23)

)1(

min

 MMn

, что также совпадает с числом сла-

гаемых в (2.22). Подстановка последнего совместно с (2.30) в соотношение (2.23) дает

асимптотическую оценку вероятности ошибки, достижимую при использовании сим-

плексных сигналов, которая в то же время, согласно (2.22), служит верхней границей ве-

роятности ошибки

)1(

min



















QMP

. (2.31)

Поскольку симплексные сигналы оптимальны по критерию минимума расстояния, то пра-

вая часть последнего выражения одновременно служит асимптотической оценкой мини-

мально возможной вероятности ошибки для случая

сигналов с фиксированными и

равными

энергиями.

Ортогональные сигналы, являющиеся еще одним примером эквидистантных, прак-

тически столь же эффективны, как и симплексные, при достаточно большом значении

Действительно, коэффициент корреляции для ортогональных сигналов равен нулю, а рас-

стояние между любой их парой

Edd

2),(

min

ss

. Используя этот факт в (2.23), по-

лучим асимптотическую оценку вероятности ошибки для

ортогональных сигналов, ко-

торая ограничивает сверху точное значение вероятности ошибки:

,)1(

















QMP

orte

. (2.32)

Сравнение (2.32) с (2.31) демонстрирует, что для выравнивания в обоих случаях

вероятностей ошибок необходимо увеличить энергию ортогональных сигналов в

)1/( MM

раз по сравнению с симплексными, т.е. энергетические потери



первых отно-

сительно вторых определяются как

)1/(  MM

. При

1M

эти потери пренебрежимо

малы и ортогональные сигналы могут рассматриваться как оптимальные. Например, при

64M

потери

63/64

, что соответствует увеличению энергии ортогональных сигна-

лов по сравнению с симплексными меньше, чем на 0.07 дБ (или 2%). Данное различие,

M=2

M=3

M=4

Рис. 2.7. Примеры симплексных сигналов.

конечно, не имеет практического значения и, если

достаточно велико, ортогональные

и симплексные сигналы могут рассматриваться взаимозаменяемыми в случае учета реали-

зационных или других причин.

Говоря об

-ичной ортогональной сигнализации (в литературе используются так-

же термины ортогональная модуляция или ортогональное кодирование) вспомним, что

максимальное число ортогональных сигналов в точности совпадает с размерностью сиг-

нального пространства, т.е.

nM 

. Поэтому в пределах общей полосы

и длительно-

сти

могут быть расположены

видео или

TW2

полосных ортогональных сигна-

лов. Дополнительное физическое обоснование удвоения числа полосных ортогональных

сигналов в сравнении с видеосигналами непосредственно следует из соотношений (2.24) и

(2.25). Построение

ортогональных сигналов вида (2.24) предполагает добавление к ним

еще

сигналов, получаемых за счет сдвига фазы несущей частоты на угол

2/

. Эта

возможность осуществима на практике только в случае, когда все сигналы детерминиро-

ваны или когерентны, что означает управление фазами несущей и возможность их ис-

пользование для идентификации сообщений. В действительности, однако, подобное не

осуществимо, поскольку либо сам передатчик, либо канал может нарушить когерентность

сигналов, в результате чего их фазы становятся случайными и поэтому не могут использо-

ваться для различения сообщений. Более подробно этот случай будет рассмотрен в 2.5.

2.4. Комплексная огибающая полосного сигнала.

Перед тем, как перевести обсуждение в область более сложных задач при передаче

–ичных сигналов, рационально несколько отклониться в сторону от основной линии с

тем, чтобы несколько больше познакомиться с описанием полосных сигналов.

Начнем с замечания о том, что вещественная огибающая

)(tS

в соотношении (2.24)

является воображаемой, т.е. служит подходящим искусственным инструментом, тогда как

только собственно сигнал

)(ts

является наблюдаемой физической реальностью. Более то-

го, выражение (2.24) не позволяет единственным образом определить огибающую сигнала

)(ts

. Действительно, как следует из (2.24), в качестве закона «фазовой модуляции» воз-

можно выбрать

)(t

, а в качестве «огибающей» –

))(2cos(/)()(

ttftstS 

, что позволит

задать данный сигнал

)(ts

. Следовательно, необходимо установить некоторые соглашения

о том, как определять понятие огибающей или амплитудной модуляции

)(tS

Общепринятой основой для определения понятия огибающей служит преобразова-

ние Гильберта. Под физическим содержанием преобразования Гильберта понимается про-

сто операция фильтрации, при которой фазы всех гармонических компонентов независи-

мо от частоты сдвигаются на один и тот же угол

2/

, а амплитуды гармоник не претер-

певают никаких изменений. В частотной области подобное преобразование означает про-

сто умножение спектра сигнала на

2/ j

для положительных и на

2/j

для отрицатель-

ных частот и, следовательно, передаточная функция фильтра Гильберта имеет вид

fjfh

sign

)(





, где

0,1sign  xx

0,1sign  xx

Непосредственное вычисление обратного преобразования Фурье приводит к импульсной

характеристики фильтра

tth

 /1)(

. Откуда во временной области преобразование

Гильберта

)(ts



сигнала

)(ts

может быть представлено в виде интеграла свертки

















)(1

)( d

. (2.33)

Используя определение преобразования Гильберта и теорему Парсеваля, не состав-

ляет труда убедиться в справедливости следующих соотношений

















)ртааниеГильбепреобразовобратное(

)(

)( d

),(),(),,(),( vuvuvuvu





. (2.34)

Первое из выражений (2.34) демонстрирует, что преобразование Гильберта не изменяет

скалярного произведения сигналов

)(),( tvtu

, тогда как второе устанавливает соотношение

между скалярными произведениями одного из сигналов и преобразования Гильберта дру-

гого.

Возвращаясь теперь к определению огибающей сигнала, положим

)()()(

tststS





. (2.35)

На первый взгляд данное определение огибающей выглядит как нечто искусствен-

ное, однако более глубокое проникновение открывает его естественность. Действительно,

как можно было бы вычислить неизвестную постоянную амплитуду

немодулированно-

го непрерывного колебания наблюдаемого сигнала

)2cos()(

 tfAtu

? Одним из воз-

можных вариантов является использование самого сигнала и его копии, сдвинутой на угол

2/

, а затем применение к ним теоремы Пифагора:

)()(

tvtuA 

. Однако сразу же

становится очевидным, что для немодулированного сигнала

)(tu

его сдвинутая по фазе

копия

)(tv

является ничем иным, как трансформантой Гильберта:

)()( tutv





. Таким об-

разом, получаем результат абсолютно совпадающий с (2.35). Возьмем теперь модулиро-

ванный сигнал

)(ts

. Его огибающая

)(tS

в момент времени

представляет собой мгно-

венное значение амплитуды. В случае полосного сигнала

)(tS

изменяется достаточно

медленно по сравнению с несущей частотой непрерывного колебания

2cos 

. Значит в

пределах достаточно малого интервала времени, примыкающего к моменту

)(ts

может

трактоваться как немодулированное гармоническое колебание с амплитудой

)(tS

. Тогда

каким способом может быть найдено значение этой амплитуды

)(tS

? Точно таким же, как

это было сделано в случае немодулированного сигнала, т.е. с помощью фазового сдвига на

угол

2/

(или преобразованием Гильберта) и применения теоремы Пифагора (2.35), ил-

люстрацией чему служит рис. 2.8. Таким образом, проблема неоднозначного понимания

огибающей полосного сигнала разрешена и определение (2.35) может использоваться

универсально.

Анализ полосных сигналов становится значительно проще при введении в рас-

смотрение еще одного удобного инструмента – комплексной огибающей (complex

envelope)

)(tS



, которая представляет собой комплекснозначную функцию времени, непо-

средственно вытекающую из соотношений (2.24) или (2.25), после установления опреде-

)(tS

)(ts



)(ts

Рис. 2.8. Определение огибающей.