Идельчик В.И. Электрические системы и сети
Подождите немного. Документ загружается.

100
Расчет
режимов линий электропередачи Гл. 3
пряжений последовательно от конца линии к началу. Для
определения токов и напряжений применяются первый за-
кон Кирхгофа и закон Ома.
Будем использовать фазные напряжения U$ и токи /.
Емкостный ток в конце линии 12, соединяющей узлы / и
~2,
У-1
и .
±7
№
Hi
Hz
?
а)
Iz
u
lciz
1
h
J-
J
b
1Z
ilci2
1
U£^
/TllZJ
x
12
h
hz^\y
ktl"
Uz
9
+
^
SiC72
1 hz
r
iz
Iz
s)
§3.2
Расчет
режима линии электропередачи
101
,
UU
k*l
\V3lizhz
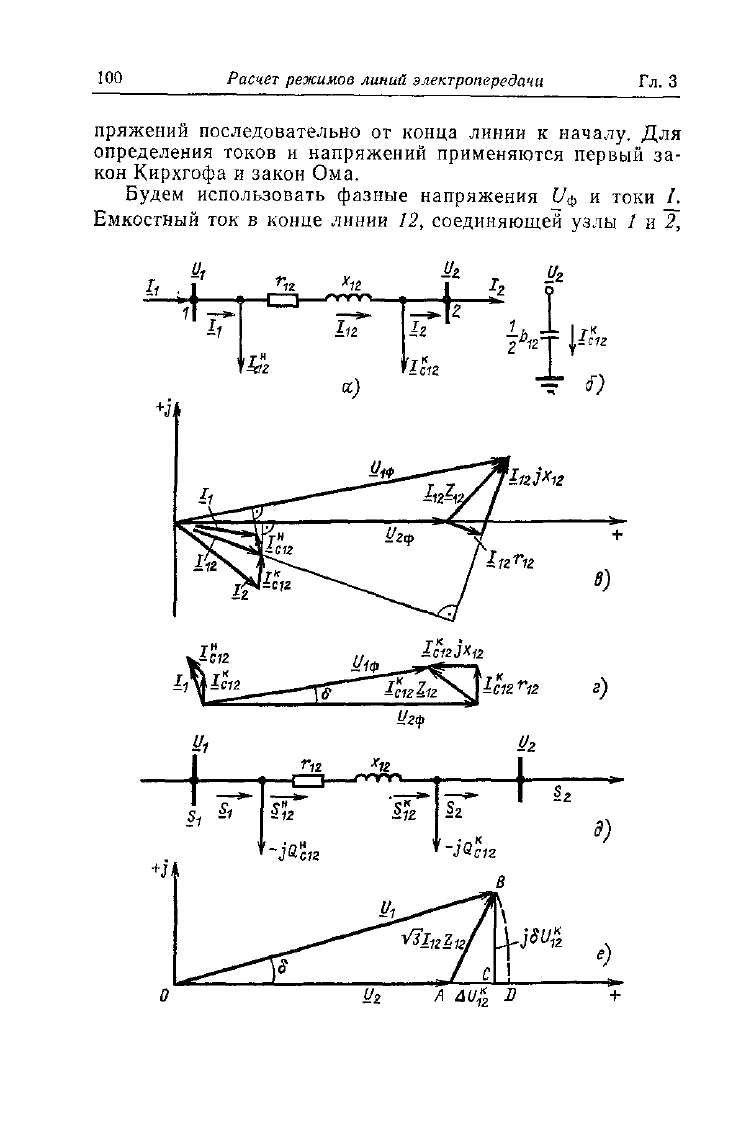
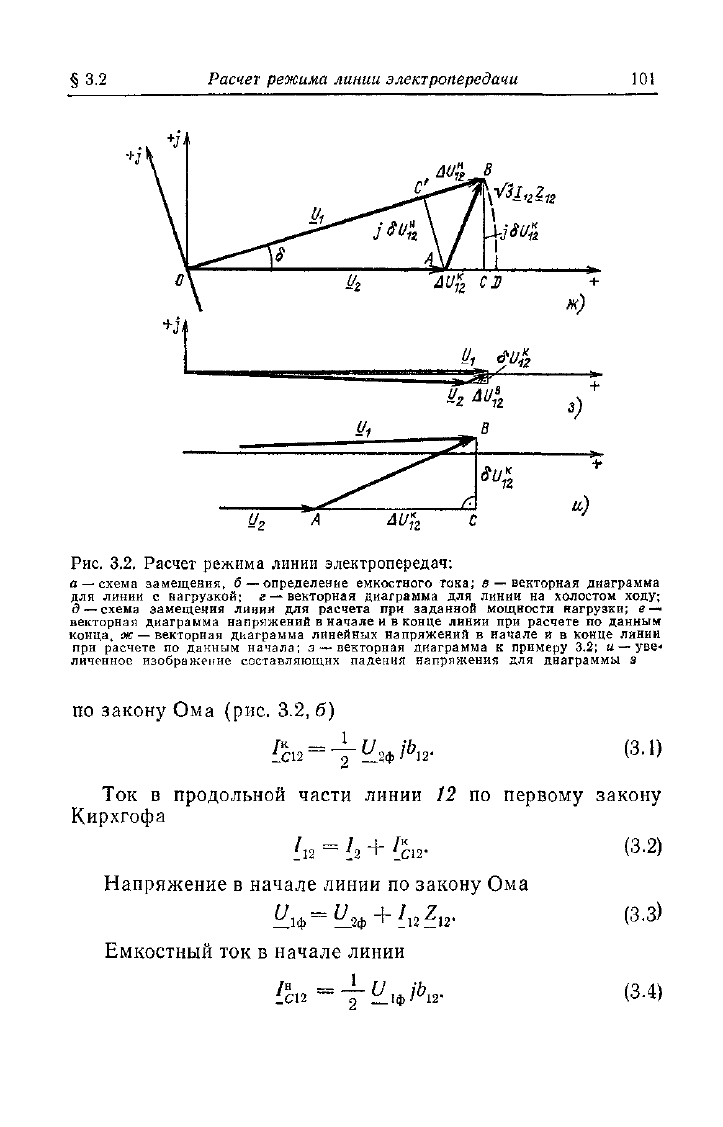
Рис.
3.2. Расчет режима линии электропередач:
а — схема замещения, б — определение емкостного тока; в — векторная диаграмма
для линии с нагрузкой; г — векторная диаграмма для линии на холостом ходу;
д — схема замещения линии для расчета при заданной мощности нагрузки; е —
векторная диаграмма напряжений в начале и в конце линии при расчете по данным
конца, ж — векторная диаграмма линейных напряжений в начале и в конце линии
при расчете по данным начала; з — векторная диаграмма к примеру 3.2; и — уве«
личенное изображение составляющих падения напряжения для диаграммы з
по закону Ома (рис. 3.2, б)
^12 = 4-^2*/Ь,
2
.
1С12 2ф /"12*
(3.1)
Ток в продольной части линии 12 по первому закону
Кирхгофа
112 12 ^ _С12-
Напряжение в начале линии по закону Ома
Емкостный ток в начале линии
/н «- _L и jh
-СП g _1ф' 12"
(3-2)
(3.3)
(3.4)

102
Расчет
режимов линий электропередачи Гл. 3
Ток в начале линии по первому закону Кирхгофа
[i-Li2 +
[
H
cu*
(3-5)
Потери мощности в линии (в трех фазах)
AS
n
=
3g
2
Z
12
.
(3.6)
Векторная диаграмма токов и напряжений (рис. 3.2, е)
строится в соответствии с выражениями (3.1)
—
(3.5).
Вна-
чале строим на диаграмме известные £/
2
ф и /
2
. Полагаем,
что и
2
ф = и
2
ф, т. е. напряжение £/
2
ф направлено по дейст-
вительной оси. Емкостный ток /£
12
опережает
1
на 90°
напряжение и
2
ф = и
2
ф. Ток Л
2
соединяет начало первого
и конец второго суммируемых векторов в правой части
(3.2).
Затем строим отдельно два слагаемых в правой час-
ти (3.3):
112 _12
=
_12
Г
\2 ~г" £
12
1
Х
\2" (3.7)
Вектор /12Г12 параллелен
1\%
Вектор I\
2
jx\
2
опережает на
90° ток /i2. Напряжение 1]щ соединяет начало и конец сум-
мируемых векторов и
2
ф, /i2^i2» /12/^12. Ток 1^
х2
опережает
Ц_\$
на 90°,/j соответствует (3.5).
В линии с нагрузкой напряжение в конце по модулю
меньше, чем в начале, £/
2
Ф<£ЛФ (рис. 3.2, в).
В линии на холостом ходу, т. е. при токе нагрузке /_2=0,
течет только емкостный ток, так как в соответствии с (3.2)
_/
12
= /*
1Я
. (3.8)
В этом случае напряжение в конце линии повышается:
^2Ф>£ЛФ-
Векторная диаграмма токов и напряжений для
такой линии приведена на рис. 3.2, г.
Задано напряжение в начале линии U
x
= const. Извест-
ны /
2
, U\, Z
12
, b
l2
. Надо определить IJ
2
, /12, AS,
2
, h. В дан-
ном случае невозможно, как ранее последовательно от кон-
ца линии к началу определить неизвестные токи и напря-
жения, используя первый закон Кирхгофа и закон Ома.
Рассчитать режим очень легко, если использовать из-
1
Термин «опережает» предполагает опережение при вращении про-
тив часовой стрелки. Например, мнимая ось опережает действительную
на 90°.

§ 3.3
Расчет режима
линии
электропередачи
103
вестное уравнение узловых напряжений (узловых потен-
циалов) для узла 2:
где У
12
— взаимная (или общая) проводимость узлов / и 2,
равная сумме проводимостей ветвей, соединяющих эти уз-
лы и взятых с обратным знаком; У
2
2 — собственная прово-
димость узла 2, равная сумме проводимостей ветвей, со-
единенных с узлом 2. Для линии на рис. 3.2, а и б
y
i2
=-Z-i; K
22
= Z-i + /V (3.10)
Из уравнения узловых напряжений (3.9) легко опреде-
лить напряжение:
U»*1&(l*-Za<Li*)< <
ЗЛ1)
а затем по закону Ома из (3.3) найти ток в линии Ij
2
, а из
(3.5),
(3.4)— ток /,.
Уравнение узловых напряжений (3.9) следует из перво-
го закона Кирхгофа.
Последовательное от конца линии к началу определение
токов и напряжений по первому закону Кирхгофа и закону
Ома можно применять только при расчетах разомкнутых
сетей. Определение напряжений из уравнений узловых на-
пряжений и затем токов в линиях по закону Ома можно
использовать для любых сетей — как для замкнутых, так
и для разомкнутых.
3.3.
РАСЧЕТ РЕЖИМА ЛИНИИ ЭЛЕКТРОПЕРЕДАЧИ
ПРИ ЗАДАННОЙ МОЩНОСТИ НАГРУЗКИ
Задано напряжение в конце линии £/
2
=
const.
Известны
(рис.
3.2,(5) мощность нагрузки 5
2
, напряжение U
2
, сопро-
тивление И ПрОВОДИМОСТЬ ЛИНИИ
Zi
2
=
ri2+/^12,
&12- НаДО
определить напряжение U
u
мощности в конце и в начале
продольной части линии S*
2
, S=
2>
потери мощности A5i
2
,
мощность в начале линии S
t
. Для проверки ограничений
по нагреву иногда определяют ток в линии /i
2
.
Расчет аналогичен расчету, приведенному в § 3.2, и со-
стоит в последовательном определении от конца линии к на-
чалу неизвестных мощностей и напряжений при использо-

104
Расчет режимов
линий
электропередачи
Гл.
3
вании первого закона Кирхгофа
и
закона
Ома.
Будем
ис-
пользовать мощности трех
фаз
и
линейные напряжения.
Зарядная (емкостная) мощность трех
фаз
в
конце линии
[см.
(В.4), (3.1)]
-
/<&2
=
Чей
^2ф
=-
у
Щ
]Ь
™
(3 12)
Мощность
в
конце продольной части линии по первому
закону Кирхгофа
Sf
2
-S
2
-/Q£
12
. (3.13)
Потери мощности
в
линии
в
соответствии
с
(В 9)
ок2
AS
12
=
3/?
2
Z
12
=
-^-Z
12
.
(3.14)
Ток
в
начале
и в
конце продольной ветви линии одина-
ков.
Мощность
в
начале продольной ветви линии больше,
чем мощность
в
конце,
на
величину потерь мощности
в
ли-
нии,
т. е.
S?
2
=
S?
2
+AS
l2
. (3.15)
Линейное напряжение
в
начале линии
по
закону
Ома
с учетом
(В.7)
равно
«/,
=
£/,
+
Уз/
12
z
l2
= и
2
+ Ц-
z
12
.
(з.
16)
Емкостная мощность в начале линии
~/Qci2=-y£/i/bi2. (3.17)
Мощность в начале линии
Si~$2-iQ*cii'
<
3
-
18
)
Задано напряжение
в
начале линии
^/
1
= const. Извест-
ны
(рис.
3.2,(5)
S
2
,
Uu_Z\2=r\z-\~jX\2,
b
l2
.
Надо определить
U
2>
S*
2
,S?
2
,AS
12
,
S,.
В данном случае невозможно последовательно
от
конца
линии
к
началу определить неизвестные токи
и
напряжения
по первому закону Кирхгофа
и
закону
Ома, так как
U
2
не-
известно. Нелинейное уравнение узловых напряжений
для
узла
2
имеет следующий
вид:

§33 Расчет режима линии электропередачи
105
Г
22
^2
+ ад = ^) =
^|--
(319)
Это уравнение можно решить
и
найти неизвестное
на-
пряжение
U
2
,
а
затем найти
все
мощности
по
выражениям
(3
12) — (3
15), (3 17), (3 18)
Способы решения нелинейных
уравнений узловых напряжений будут рассмотрены
в
гл
9
Однако можно осуществить приближенный расчет
в
два
этапа
1-й
этап
Предположим,
что
^
2
=
^ом> (3 20)
и определим потоки
и
потери мощности аналогично выра-
жениям
(3
12) — (3
15),
используя
(3 20):
~]Qcu=--~
U
^}bi2;
(3 21)
§А2
=
$2 —
/^С12
*
(3 22)
<^к2
А5
12
= -f-
?
12
; (3 2
)
—
и
2
ном
&
=
$2
+
А
!?
12
.
(3 24)
2-й этап Определим напряжение
U
2
по
закону
Ома, ис-
пользуя поток мощности
S^
2
(рис 3
2,(5), найденный
в
1-м
этапе
Для
этого используем закон
Ома
в
виде
(3 16), но
выразим
ток /i2
через
S"
n
и U\\
4>-4i-
1^з/
12
г„ = и,- &-z
l2
.
о25)
_1
Потоки мощности
на 1-м
этапе определены приближен-
но,
поскольку
в
(3 21)
и
(3 22)
вместо
U
2
использовали
£Люм Соответственно напряжение
U
2
на
2-м
этапе также
определено приближенно,
так
как
в
(3 25)
используется
приближенное значение
S"
2
,
определенное
на 1-м
этапе
Возможно итерационное повторение расчета,
т е
повто-
рение
1-го
и
2-го
этапов
для
получения более точных зна-
чений мощностей
и
напряжений
Как
правило,
при
прове-
дении расчетов вручную,
а
не на ЭВМ,
такое уточнение
не
требуется

106
Расчет
режимов линий электропередачи Гл. 3
Пример 3.1. Нагрузка 5
2
=15+/10 MB-А питается от шин электро-
станции по одноцепной линии ПО кВ длиной 80 км. Схема замещения
линии показана на рис. 3.2, д, ее параметры /-12=24,48 Ом, x
!2
=34,72 Ом,
b
l2
=208,8-Ю
-6
См. Напряжение иа шинах электростанции t/
L
= 116 кВ.
Определим мощность Si, вырабатываемую электростанцией, и на-
пряжение в конце линии U
2
. Расчет проведем в два этапа.
1-й этап. Емкостную мощность линии, потери и потоки мощности
в ней найдем по номинальному напряжению, т. е. по выражениям
(3.21) — (3.24). При этом
Q£
12
= -— 110
2
-203,8-10-
6
= 1,26 Мвар.
Мощность в койце линии
5j[2=-S
2
—/Q£
12
=
15
+ /10 —/1,26=
15
+/8,74 MBA.
Потери мощности в линии
15
2
+ 8,74*
ДР
12
= -H-i 24,48 = 0,61 МВт;
12
ПО
2
15
2
+ 8,74
2
AQ
12
= -!_-_: 34,72 = 0,86 Мвар.
Мощность в начале линии
5?2 = ^
2
+ AP
12
+ /AQ
12
=15 + /8,74 + 0,61+/0,86 =
= 15,61+/9,6 МВ-А.
Мощность с шин электростанции
§.i=§i2 — iQ
H
ci2= 15,61+/9,6 — /1,26= 15,61 +/8,34 МВ-А.
2-й этап. Напряжение в конце линии определим из уравнения
(3.25):
U п
6
_
15
'
61
~^'
9
'
6
(24,48 + /34,72) = 109,8-/2,65 кВ.
116
Модуль напряжения
U
2
= ]Ло9,8
2
+ 2,65
2
= 109,8 кВ.
3.4.
ПАДЕНИЕ И ПОТЕРЯ НАПРЯЖЕНИЯ В ЛИНИИ
На рис. 3.2, е приведена векторная диаграмма для ли-
нейных напряжений в начале и в конце линии 1)\ и
1]%
Эта
диаграмма аналогична диаграмме на рис. 3.2, в.
\

§3.4
Падение и потеря напряжения в линии
107
Падение напряжения — геометрическая (векторная)
разность между комплексами напряжений начала и конца
линии. На рис. 3.2, е падение напряжения — это вектор
AS,
т. е.
АВ = U
t
— U
2
= Уз /
12
Z
12
. (3.26)
Продольной составляющей падения напряжения Д£/*2
называют проекцию падения напряжения на действитель-
ную ось или на напряжение U
2
, &Uf
2
=AC на рис. 3.2, е.
Индекс «к» означает, что A£/i2 — проекция на напряжение
конца линии U
2
. Обычно Д£/*
2
выражается через данные
в конце линии: U
2
, Р12, Qn-
Поперечная составляющая падения напряжения dll^ —
это проекция падения напряжения на мнимую ось, 6Un —
= СВ на рис. 3.2, е. Таким образом,
Ц_
г
— U
2
=
]/а/
12
Z
i2
-
Д£/'<
2
+
jbU
K
u
.
(3 27)
Часто используют понятие потеря напряжения — это ал-
гебраическая разность между модулями напряжений на-
чала и конца линии. На рис. 3.2, е
U\—U
2
=AD.
Если попе-
речная составляющая 8U*2 мала (например, в сетях
^ном^ПОкВ), то можно приближенно считать, что потеря
напряжения равна продольной составляющей падения на-
пряжения.
Расчет режимов электрических сетей ведется в мощно-
стях, поэтому выразим падение напряжения и его состав-
ляющие через потоки мощности в линии.
Известны мощность и напряжение в конце линии (рас-
чет напряжения в начале линии по данным конца). Выра-
зим ток в линии 1\2 в (3.27) через мощность в конце про-
дольной части линии 5^
2
и напряжение^:
*»-т%-
(328)
В результате получим

108
Расчет
режимов линий электропередачи Г л 3
'
Q
'
2
(r» + ixj=
J?
»
,
» +
qf
'*» +
+ ; Т'*»-<&'•» - Д£/Ь + /Ы/&. (3 29)
Приравняв в (3 29) действительные и мнимые части, по-
лучим выражения продольной и поперечной составляющих
падения напряжения по данным конца
АЕ/?
2
= ^'" + <&*" . (3 30)
6t/?
^12^:0^12
(331)
и*
Напряжение в начале линии
U, - Uj + AU-
2
+
/6£/f
2
,
(3 32)
где
U_2
известно;
АЩ
2>
6U^
2
определяем из (3 30) и (3 31).
Соответственно модуль и фаза напряжения в начале ли-
нии (см рис 3 2, е)
U
x
= V(U
2
+ AU$
2
y+(M}
2
y; (3 33)
tg6 = —•. (3 34)
U
2
+ AU«
2
Определение напряжения в начале линии по данным
конца по выражениям (3 32), а также (3 30), (3 31) экви-
валентно использованию закона Ома
Пример 3.2. Определим падение и потерю напряжения в линии, рас-
смотренной в примере 3 1, по известным мощности нагрузки
S
2
=15
+
+/ 10 MB А и напряжению в конце линии U
2
= 109,8—/ 2 65 кВ
Используя параметры линии, а также мощность в конце линии
S*
2
, приведенные в примере 3 1, по (3 30), (3 31) найдем продольную
и поперечную составляющие падения напряжения по данным конца
А к
15 24,48 + 8,74 34,72 „ ,
(
„
Д(/
к ;—j^ : = 6,11 кВ,
12
109,8
15 34,72 — 8,74 24,48
109,8
Щ
2
=
1
—7ZT7, -
J
—* =
2
>
8 кВ
-

§ 3.4 Падение и потеря напряжения в линии 109
Напряжения Ui и £/
2
приведены на рис. 3.2, з. В большем мас-
штабе продольная и поперечная составляющие падения напряжения
изображены на рис 3 2, и
Напряжение в начале линии по (3.32) равно
и
г
*=
109,8 —/2,65 + 6,11 +/2,8» 115,9 + /0,15 кВ.
Модуль напряжения в начале линии
U
t
=]Л15,9
2
+ 0,15?= 115,9 кВ.
Потеря напряжения
^ — £/2=115,9—109,8 = 6,1 кВ.
Известны мощность и напряжение в начале линии (рас-
чет напряжения в конце линии по данным начала). Напра-
вим U\ по действительной оси, т. е. примем, что
U\
—
U
(рис.
3.2, ж). На рис. 3.2,
ж
изменилось положение осей
в сравнении с рис. 3.2, е. Продольная составляющая паде-
ния напряжения Д(7?
2
=ВС — это проекция падения на-
пряжения на действительную ось или на 1)\. Поперечная
составляющая падения напряжения б(7?2 =АС — это про-
екция падения напряжения на мнимую ось. Один и тот же
—>
вектор падения напряжения АВ проектируется на различ-
ные оси. Поэтому
Д<У?
2
4=Д<7?
2
,
6U
H
12
=hW
2
.
Если выразить ток в линии 1
12
аналогично (3.28) через
известные в данном случае мощность в начале продольной
ветви линии 5"
2
и U\
t
то получим выражения, аналогичные
(3.30),
(3.31):
А£7?
2
~
^'" + <&*" .
(
з.з5)
ШЪ =
PW
~
Q
"
2ri2
. (3.36)
Напряжение в конце линии
4.2
=
У_1
~
Л
^
2
— 1Щ
2
>
(З-
37
)
где Uj известно; Д£/"
2
, Ы)\
2
определяются из (3.35), (3.36).
Модуль и фаза U
2
равны
