Идельчик В.И. Электрические системы и сети

Подождите немного. Документ загружается.

130

Расчет

режимов линий электропередачи Гл. 3;

где 5'/

— мощность в начале линии; S*

— мощность в кон-

це линии.

Мощность на головном участке (рис. 3.9, ж) определя-

ется следующим выражением:

где k — порядковый номер нагрузки; п—1 — количество

нагрузок;

5) пренебрегаем поперечной составляющей падения на-

пряжения bV. Это значит, что не учитывается сдвиг напря-

жения по фазе между отдельными узлами сети. Векторная

диаграмма напряжений приведена на рис. 3.9, з. При рас-

чете учитывают лишь продольную составляющую падения

напряжения Д(У, которая равна потере напряжения:

6) расчет потери напряжения ведется по

HCm

а не по

действительному напряжению сети:

^ном

где Р\2 — активная мощность в линии; Q

—реактивная

мощность в линии; г

— активное сопротивление линии;

#12

— реактивное сопротивление линии.

3.11.

ОПРЕДЕЛЕНИЕ НАИБОЛЬШЕЙ ПОТЕРИ НАПРЯЖЕНИЯ

Рассмотрим схему замещения распределительной сети,

приведенную на рис. ЗЛО. При электрическом расчете из-

вестны мощности в узлах Sk, напряжение в начале линии

Uи сопротивление участков линии Z*/, где k — номер узла

начала участка линии (£=1,2); / — номер узла конца

"sjT \ Тгз s* • 0,6¥км FT

0,5

КМ

•

\ Р=1930кЪт

а) Р

=1880кВт б)

Рис.

3.10. Распределительная сеть:

—

схема замещения; б —кабельные линии

§3.11 Определение наибольшей

потери

напряжения 131

участка линии (/ =

3). Надо определить напряжения в уз-

лах и мощности на участках линии Sk,.

Мощности

S_ki

определяются по первому закону Кирх-

гофа:

= S

; 5

^2 • _v (3.57)

При этом активные и реактивные мощности на участках

линии равны

= Р» Ри = Рг + Р» (3-58)

3 = Q

; Qi» =

Q»

Q».

(3.59)

При расчете напряжений необходимо проверить, чтобы

самое низкое из напряжений в узлах было не меньше до-

пустимого. Вместо определения самого низкого из напря-

жений в узлах обычно определяют наибольшую потерю

напряжения. Разница между напряжениями источника пи-

тания и узла с самым низким напряжением называется наи-

большей

потерей

напряжения. Для сети на рис. 3.10

Д£/

=и

—и

Наибольшая потеря напряжения в общем случае

где

ts.Uk!

— потери напряжения на участке линии; m —

число участков линии, и может быть вычислена так:

Здесь

гщ

— активное сопротивление участка линии; x

j —

реактивное сопротивление на участке линии; P

Qkj

—

активная и реактивная мощности на участке линии.

Если выразить потоки мощности в линии через мощно-

сти нагрузки, то выражение (3.61) можно записать проще.

Для этого запишем (3.61) для схемы рис. 3.10, а так:

12 r

~Ь Qia

\л |

°23

Угз *23

/о cm

^ном ^ном

Придадим этой формуле другой вид, учтя (3.57)

—

(3.59)

и обозначив

= г

; (3.63)

= г

1г

+ г

, (3.64)

132 Расчет режимов линий электропередачи Гл.^3

Х%

— -^12» (З.Ьо)

*з = Хц + х

2в

. (3.66)

Для этого подставим выражения (3.58) — (3.59) в (3.62)

и используем (3.63) — (3.66). Тогда

/ли

нб

= 1-

^ном

I ^з (

—

г)

Фз

(

— *а)

/о cj\

"ном

или

Т 1

Р%

2 4~ Q2 *2 I °3

3 ~t~ У3*3 __

нб .. |

(РкГЦ

QhXh)

« ^ (3.68)

<^ном

где РЙ, Qk — мощность нагрузки k-то узла;

ГЙ,

-*:&— сопро-

тивление от. узла / до узла k; n — количество узлов.

Формула (3.68) справедлива для любого количества

узлов.

Если сечения проводов Fkj на всех участках линии оди-

наковы, то

п п

*°

"iw

(

Го

К + х

° ^

69)

fe=2 й=2

где

/Й

— расстояние от узла 1 до узла k.

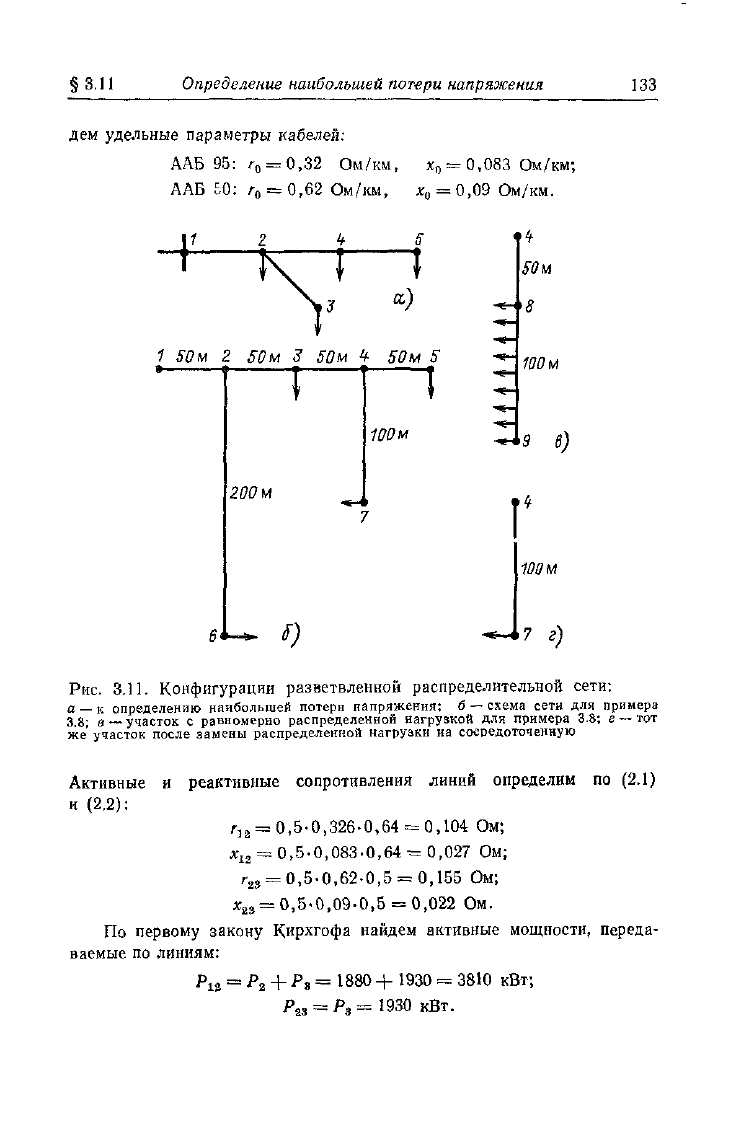
Рассмотрим, как определяется наибольшая потеря на-

пряжения в разветвленной сети (рис. 3.11, а). Для этого

определим потери напряжения Д£Лз, kU\b'-

Д£/

1з

= MJ

+ Д*/

да

дс/

1а

+ дг/

д£/

Если Д£/

4-ЬЛ^45>Д£Л>з, то At/

>Af/i3 и Ai/is — наи-

большая потеря напряжения.

Пример 3.7. Электрическая сеть 10 кВ выполнена кабельными ли-

ниями (рис. 3.10,6). Коэффициенты мощности нагрузок cosq>=0,96.

Найдем наибольшую потерю напряжения в сети. По табл. П.2 най-

§3.11

Определение наибольшей

потери

напряжения

133

дем удельные параметры кабелей:

ААБ

95: л

= 0,32

Ом/км,

0,083 Ом/км;

ААБ

£0: г

= 0,62

Ом/км,

0,09 Ом/км.

1 50м Z 50м 3 50м 4 50м 5

»-—

• J

100 м

ff<

ZOOM

•*-i

5"0м

100 м

•*±9

в)

•4

100 М

7 г)

Рис.

3.11.

Конфигурации разветвленной распределительной сети:

—

к определению наибольшей потери напряжения; б

—

схема сети для примера

3.8;

—

участок с равномерно распределенной нагрузкой для примера 3.8; е

—

тот

же'

участок после замены распределенной нагрузки иа сосредоточенную

Активные

реактивные сопротивления линий определим

по (2.1)

и (2.2):

1а

0,5-0,326-0,64

0,Ю4

Ом;

0,5-0,083-0,64 -=0,027

Ом;

0,5-0,62-0,5

0,155

Ом;

0,5-0,09-0,5

0,022

Ом.

По первому закону Кирхгофа найдем активные мощности, переда-

ваемые

по

линиям:

= р

+ р

1880

1930

3810

кВт;

9Ч

= Р, =

1930

кВт.

Расчет режимов линий электропередачи Г л 3

По активным мощностям и коэффициенту мощности находим реак-

тивные мощности в линиях

= P

tgcp = 3810-0,292= 1113 квар;

= p

tg ф = 1930-0,292 = 564 квар.

Потери напряжения в линиях 23 и 12

1930-0,155 + 564.0,022

= ' ^ = Л ,2 В;

(1880 + 1930) 0,104 + (1113 + 564) 0,027

= — = 44,2 В,

Наибольшая потеря напряжения в сети

Д1/

б =

^12 + Д^23^31,2 + 44,2 = 75,4 В;

0,0754

ДУнб%

-[f-

° = °'

•

Пример 3.8. Определим наибольшую потерю напряжения в сети

рис 3 11,6 и сопоставим ее с допустимой (Л£/

ДО

п=7 %) Сеть имеет на-

пряжение 380 В, выполнена алюминиевыми проводами Линии сооруже-

ны на деревянных одностоечных опорах, провода крепятся на штыревых

изоляторах и располагаются в вершинах равностороннего треугольника

со стороной 600 мм Длины участков приведены на схеме. Нагрузки

и их коэффициенты мощности имеют следующие значения

Номер узла 3 5 6 7

На1рузка, кВт 25 25 15 15

ccsq) . 1 0,8 0,8 1

Магистраль 15 выполнена проводом одного сечения А 50 (r

—

0,63

Ом/км, х

=0,325 Ом/км). Ответвление 26 — проводом А 16 (г

= 1,96 Ом/км, лг

=0,358 Ом/км), ответвление 47 — проводом А 25

(г

= 1,27 Ом/км, Ха*=0,345 Ом/км).

Определим активные и реактивные составляющие нагрузок:

= 25+/25 0,75 = 25+ /18,75 кВ А;

= 15 + / 15 0,75= 15 + /11,25 кВ А

Нагрузки 3 и 7 имеют только активные составляющие. Найдем по-

терю напряжения в магистрали 15 по выражению (3 61)

(80 + 65+40 + 25)50 0,63+ (30+ 18,75 +

AC/m =

380

+ 18,75+18,75)50-0,325 =21,1 В.

§3.12

Расчет

линии с разномерно распределенной нагрузкой 135

Потери напряжения от центра питания / до узлов 6 и 8 по (3.61)

равны

15-200-1,96+ 80-50-0,63+ 11,25-200-0,358 + 30-50-0,325

Л(Л« =

At/

380

= 25,51 В;

(80 + 65 + 40) 50-0,63 + 15-100-1,27 + (30 + 18,75 +

380 ~*

+ 18,75)50-0,325

п я

-*—

;

— • =23,2 В.

Наибольшая потеря напряжения в сети составляет ЛС/

б=Д(/

)В

25,5

В или Д(/

Нв

= (25,5/380) -100=6,71 %, что не превосходит до-

пустимого значения.

3.12.

РАСЧЕТ ЛИНИИ С РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ

НАГРУЗКОЙ

Рассмотрим случай, когда по всей длине линии на рав-

ных расстояниях подключены равные нагрузки (например,

городское уличное освещение). При определенных усло-

виях такую линию можно рассматривать как линию с рав-

номерно распределенной нагрузкой.

Определение потерь мощности. Рассмотрим линию на

рис.

3.12, а, где i — удельная нагрузка, т. е. токовая на-

грузка единицы длины линии, А/м; dl— элемент длины;

L — длина всей линии, м. Для элемента длины dl токовая

Ф .

TTTTjfJfJ

f) h

1/2

Рис.

3.12. Расчет режима линии с равномерно распределенной на-

грузкой:

—

схема линии с распределенной нагруакой; 6

—

схема той же линии с сосредо-

точенной нагрузкой; в —схема для расчета потерь мощности; г —схема для рас-

чета потерь напряжения

136 Расчет режимов линий электропередачи Гл. 3

нагрузка равна idl. Для всей линии суммарный ток нагруз-

ки равен

idl

—

iL = I.

Через первый от начала линии элемент длины течет

весь суммарный ток нагрузки /. Чем дальше от начала ли-

нии, тем меньше протекающий в линии ток. В последнем

элементе длины течет ток i. В элементе длины dl на рас-

стоянии / от начала линии протекает ток i (L—/). Сопро-

тивление элемента длины равно

dl,

где г

— удельное ак-

тивное сопротивление провода. Потери мощности в трех

фазах рассматриваемого элемента длины равны

3[i(L — t)]

dl.

Проинтегрировав это выражение от 0 до L, получим по-

тери мощности в линии:

АР = \ 3 li

(L —

/)Рr

dl-=— 3r

(L - If

Потери мощности в линии с сосредоточенной нагрузкой

на рис. 3.12, б определяются следующим выражением:

AP = 3/

Таким образом, в линии с равномерно распределенной

суммарной нагрузкой / потери в 3 раза меньше, чем в ли-

нии такой же длины с сосредоточенной нагрузкой /, при-

ложенной в конце линии. Поэтому при расчетах потерь

мощности линию с равномерно распределенной нагрузкой

заменяют линией с сосредоточенной суммарной нагрузкой,

приложенной в середине линии (рис. 3.12, в).

Определение потери напряжения. В линии с равномер-

но распределенной нагрузкой обозначим через р удельную

активную мощность нагрузки на единицу длины линии,

Вт/м. Суммарная активная мощность нагрузки всей линии

равна

j pdl = pL = P.

§3.12

Расчет

линии с равномерно распределенной нагрузкой 137

Будем считать, что в сети реактивная мощность не про-

текает. Через элемент длины dl на расстоянии / от начала

(рис.

3.12, а) протекает активная мощность p(L—/). Поте-

ря напряжения в этом элементе длины равна

(L —

dl/U

H0M

Проинтегрировав это выражение, получим потерю напря-

жения в линии с равномерно распределенной нагрузкой:

p(L

—

t)r

_ pr

(L-/)

L ^pr

L* __ Pr

^ном

^ном ^

Потеря напряжения в линии длиной L с сосредоточен-

ной нагрузкой Р равна

L/U

H0M

Таким образом, потери напряжения в линии с равномер-

но распределенной суммарной нагрузкой р равны потерям

напряжения в линии с сосредоточенной нагрузкой Р, при-

ложенной в середине линии (рис. 3.12,г).

Продолжение примера 3.8. Определим наибольшую потерю напря-

жения в сети на рис. 3.11,6 при условии, что к узлу 4 присоединено не

ответвление 47, а ответвление 489 с равномерно распределенной нагруз-

кой на рис. 3.11,6. Удельная нагрузка на линии 89 равна 0,15 кВт/м,

casq>=l. Длины участков ответвления приведены на рис. 3.11, е.

При определении потери напряжения заменим равномерно распре-

деленную нагрузку на участке 89 сосредоточенной нагрузкой S

прило-

женной в середине линии 89: ~

=0,15-100-4-/0 = 15+/0 кВ-А.

Полученная в результате замены линия 47 с сосредоточенной на-

грузкой изображена на рис.

3.11,

г. Дальнейший расчет наибольшей по-

тери напряжения совпадает с примером 3.8.

3.13. РАСПРЕДЕЛЕНИЕ ПОТОКОВ МОЩНОСТИ И НАПРЯЖЕНИЙ

В ПРОСТЫХ ЗАМКНУТЫХ СЕТЯХ

Ранее рассматривались разомкнутые сети. Ниже будут

рассматриваться замкнутые сети. Напомним, что в разомк-

нутых сетях все узлы получают питание только по одной

ветви, что видно из примеров неразветвленной разомкну-

той сети (рис. 3.13,о) и разветвленной разомкнутой сети

(рис.

3.13,6).

В простых замкнутых сетях есть узлы, питающиеся по

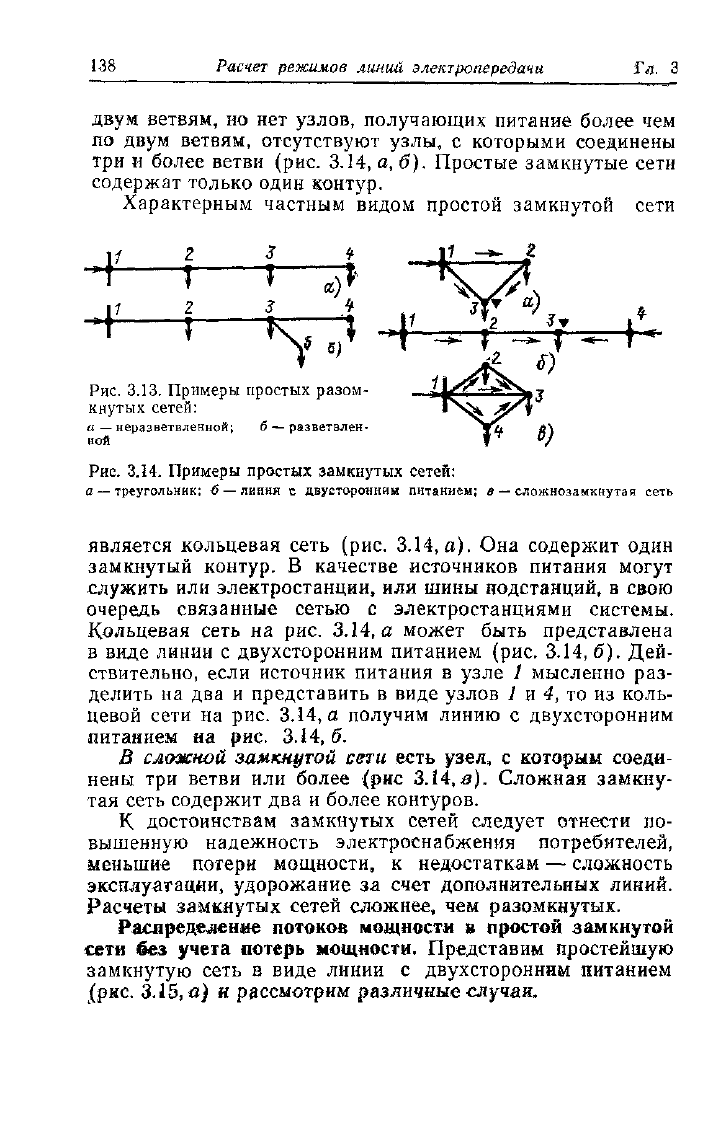
138 Расчет режимов линий электропередачи Гл. 3

двум ветвям, но нет узлов, получающих питание более чем

по двум ветвям, отсутствуют узлы, с которыми соединены

три и более ветви (рис. 3.14, а, б). Простые замкнутые сети

содержат только один контур.

Характерным частным видом простой замкнутой сети

V г з » if -*• /

—*—*-"**

Рис.

3.13. Примеры простых разом-

»|^^--^S.j

к нуты х сетей: *

^ ^т

—

неразветвленной; б

—

разветвлен- jfu 6\

ной ?

«у

Рис.

3.14. Примеры простых замкнутых сетей:

а — треугольник; б

—

линия с двусторонним питанием; в

—

сложнозамкнутая сеть

является кольцевая сеть (рис. 3.14,а). Она содержит один

замкнутый контур. В качестве источников питания могут

служить или электростанции, или шины подстанций, в свою

очередь связанные сетью с электростанциями системы.

Кольцевая сеть на рис. 3.14, а может быть представлена

в виде линии с двухсторонним питанием (рис. 3.14, б). Дей-

ствительно, если источник питания в узле / мысленно раз-

делить на два и представить в виде узлов / и 4, то из коль-

цевой сети на рис. 3.14, а получим линию с двухсторонним

питанием на рис. 3.14, б.

В сложной замкнутой сети есть узел, с которым соеди-

нены три ветви или более (рнс 3.14,в). Сложная замкну-

тая сеть содержит два и более контуров.

К достоинствам замкнутых сетей следует отнести по-

вышенную надежность электроснабжения потребителей,

меньшие потери мощности, к недостаткам — сложность

эксплуатации, удорожание за счет дополнительных линий.

Расчеты замкнутых сетей сложнее, чем разомкнутых.

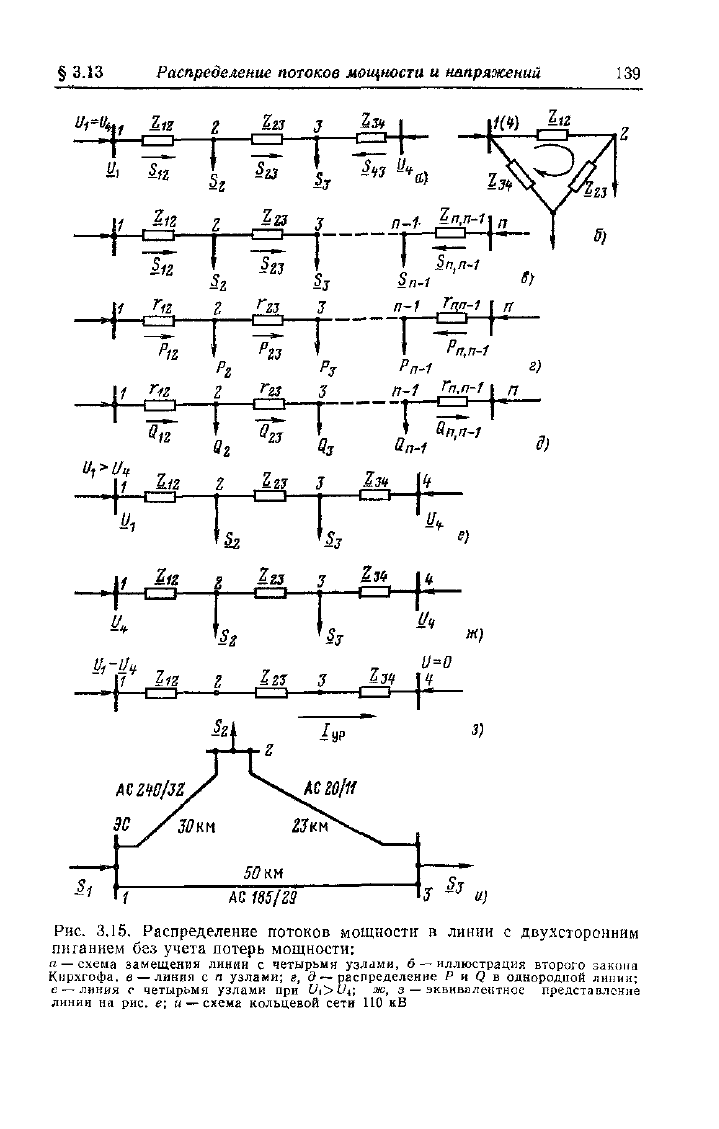
Распределение потоков мощности в простой замкнутой

сети без учета потерь мощности. Представим простейшую

замкнутую сеть в виде линии с двухсторонним питанием

(рис.

3.15, а) и рассмотрим различные случаи.

§3.13 Распределение потоков

мощности

и напряжений 139

АС 185/29

Рис.

3.15. Распределение потоков мощности в линии с двухсторонним

питанием без учета потерь мощности;

а — схема замещения линии с четырьмя узлами, 6 — иллюстрация второго закона

Кирхгофа, в — линия с п узлами; г, д — распределение Р и Q в однородной линии;

е — линия с четырьмя узлами при Ui>Ut; ж, з — эквивалентное представление

линии на рис. е; и — схема кольцевой сети 110 кВ