Houze Robert A., Jr. Cloud Dynamics

Подождите немного. Документ загружается.

(12.36)

12.2 Wave Clouds Produced by Long Ridges 519

fluid

"If containing a hydraulic jump, as idealized in Fig. 12.12. The volume "If is

bounded by

and X2 and y and y +

Lly

in a coordinate system that moves with the

discontinuity in fluid height. The flow is assumed to be homogeneous (i.e., of

constant density) and steady state in this moving coordinate system.

We first consider the mass continuity in the fluid containing thejump by averag-

ing (12.28) to obtain

Q ;:

iiH

= constant

(12.35)

Next,

we consider the conservation of momentum in the mass of fluid contained

"If. The equation of motion governing the mean fluid motion is obtained by

applying the averaging procedure described in Sec. 2.6 to (2.1), ignoring Coriolis

and molecular frictional forces and recalling that the density of an incompressible

fluid is constant. The result is

Dv P -

- =

-V--gk+~

Dr p

Integrating the x-component of (12.36) over the mass of fluid in "If in the moving

coordinate system, with substitution from (12.35), and recalling that the pressure

at a given level is the weight of the fluid above leads to

(12.37)

(12.38)

where

Lly(Z:~2H2)

III

?Jt

"If

and

is the x-component of

'#.

The quantity Q} in (12.37) can be seen to arise

from the drag of turbulence or other small-scale motion. The first term in (12.37)

arises from the combination of the horizontal pressure gradient acceleration and

the horizontal advection of u,

Now we may examine the energy of the mean flow in the volume

"If containing

the hydraulic jump. Under the assumed steady-state, two-dimensional conditions,

with uniformity in the y-direction, the kinetic energy equation obtained by taking

v·(12.36) is

(12.39)

where

(12.40)

A negative value of

q!J

indicates that energy is being dissipated locally. Integration

of (12.39) over the mass of fluid in the volume

"If bounded by

and X2 and y and

520 12 Orographic Clouds

y + Ay leads to

Iff

PVn[~Z

+ :Z

+gz+

'V S

(12.41)

(12.42)

where

is the outward relative velocity component normal to the surface S

surrounding the volume Y.

the term on the right is negative, there is a net

convergence of energy into the fluid volume, and this convergence must be

matched by net dissipation in the volume in order to maintain the steady state.

Carrying out the integration on the right-hand side of (12.41), with substitution

from (12.35) and (12.37) and again letting the pressure be given by the weight of

the fluid above, leads to

Iff

- 3 pAyQQF

)

d"lf = pAyQg(H

- Hz) _

2H1H1

In the case represented in Fig. 12.12, Q> 0 and

- Hz <

The right-hand side

of (12.42) is therefore negative, indicating a net loss of energy in the volume

containing the jump. Moreover, (12.42) is still obtained even if the volume

"If is

made arbitrarily small by moving

and Xz as close as we like to the jump in fluid

height. Thus, it is clear that all the energy loss occurs

at the jump. This result

implies that dissipative forces must be active in the vicinity of the jump in order to

conserve energy. Thus, (12.42) is a clear indication that some energy dissipation

must occur in the vicinity of the jump. The loss of energy at the jump is effected by

turbulence and/or downstream-propagating waves, which are allowed if the flow

to the right of the jump is subcritical.

is for this reason that rotor clouds located

at a hydraulic jump can be quite turbulent and are known by pilots to be a sign of

dangerous zones for light aircraft. Examples of spectacular rotor clouds were

shown in Figs. 1.23 and 1.24.

The primary dynamical characteristics of rotor clouds that can be explained by

the foregoing theory are the strong upward air motion that occurs at the hydraulic

jump and the strong turbulence or gravity wave motion required to accomplish the

dissipation of energy at the jump. There is some belief, especially from sail plane

pilots, that the air in the rotor clouds overturns around a horizontal axis normal to

the mean flow direction.

is from this aspect that the name rotor cloud is derived.

However, neither careful observation of rotor clouds nor model simulations have

yet confirmed whether or not such rotation is a predominant feature of the in-

cloud air motions.

12.3 Clouds Associated with Flow over Isolated Peaks

We have seen that small-amplitude wind perturbations produced by flow over a

long ridge take the form of vertically propagating and trapped lee waves. Some-

what similar responses occur in flow over an isolated mountain peak. However,

12.3 Clouds Associated with Flow over Isolated Peaks

521

parcel and wave motions are not restricted to only the x- and z-directions. Compo-

nents of motion in the y-direction can appear as the air flows around as well as

over the three-dimensional peak.

To illustrate this fact, we again consider the vorticity about the y-axis generated

as a basic unidirectional horizontal flow encounters and passes over the mountain.

We neglect Coriolis effects and use the steady-state form of the three-dimensional

Boussinesq y-vorticity equation (2.58)

(12.43)

which states that the advection of g is balanced by baroclinic generation

(-B

stretching gv

and tilting

(~vz

7JVx)'

We will concern ourselves first with small-

amplitude motions by linearizing this equation about a purely horizontal, unidirec-

tional mean wind

u(z) and mean lapse rate e; To illustrate the essential physics

retained under linear conditions, we first linearize the right-hand side of (12.43).

The result is

(12.44)

This relation differs from the two-dimensional form (12.3) in that the stretching of

vorticity contained in the basic-state shear by perturbations lateral to the basic-

state current

(uzv

)

now appears on the right-hand side, along with the baroclinic

generation of

g associated with air moving up and down adiabatically and the

advection of

gby the y-component of motion (vg

on the left-hand side. If we now

linearize the left-hand side of the equation and substitute from the perturbation

form of the three-dimensional Boussinesq continuity equation (2.55), we obtain,

after some rearrangement,

(12.45)

The only differences between this result and the two-dimensional case [cf. Eq.

(12.4)] are the first and last terms, which involve the perturbation of the flow

lateral to the basic current.

Since the variable

v is now involved, a further physical relationship is required

to close the system of equations.

For

this, we turn to the vertical vorticity equa-

tion (2.59), which under the present steady-state linearized conditions with no

Coriolis effects reduces to

(12.46)

which says that the horizontal advection of vertical vorticity by the basic-state

flow is

just

offset by the tilting of the base-state shear by y-variability of w. This

relation may be rewritten as

(12.47)

522 12 Orographic Clouds

Taking the horizontal Laplacian

V'iJ

+ a

2 of (12.45), making use

ofthe

mass continuity equation (2.55), and substituting from (12.47) leads to

(12.48)

where

is the three-dimensional Laplacian. As in the two-dimensional case

(12.4), this vorticity equation has solutions of the forms of evanescent, vertically

propagating and trapped waves. However, the presence of the perturbation mo-

tions lateral to the basic current leads to the waves being distorted into interesting

configurations, which can affect the forms of clouds that develop in the waves.

The vertically propagating modes can be obtained by further simplifying the

problem such that

it does not vary with height. In this case, the Scorer parameter

given by (12.5) reduces to

(12.49)

and (12.48) becomes

which has solutions of the form

w =

w/(kx+

jy+mz)

with the following relation among k,

and m:

2 k

m = 2

£-k

(12.50)

(12.51)

(12.52)

which is similar to (12.7), except for the factor

+ j2)/k

•

Thus, m

depends

onj

as well as k.

From (12.52) it is apparent that, as in the two-dimensional case, vertically

propagating or evanescent waves occur depending on whether

> k

or e

< k

respectively. As in the two-dimensional case, we can proceed by assuming some

specific form for the surface topography and disallowing downward energy propa-

gation at the top boundary. Figure 12.13 shows an example of the vertical motion

pattern associated with steady, constant

and constant it flow over a wide (e >

k) mountain. Alternating boomerang-shaped regions of upward and downward

motion occur downwind of the peak. This pattern of vertical motion occurs even if

the mountain is wide enough that the flow response is hydrostatic. That is, in the

three-dimensional hydrostatic case, the wave disturbance is not confined to the

region directly over the mountain. In this vertical motion pattern, a boomerang- or

horseshoe-shaped cloud can be observed in the lee of the mountain. The example

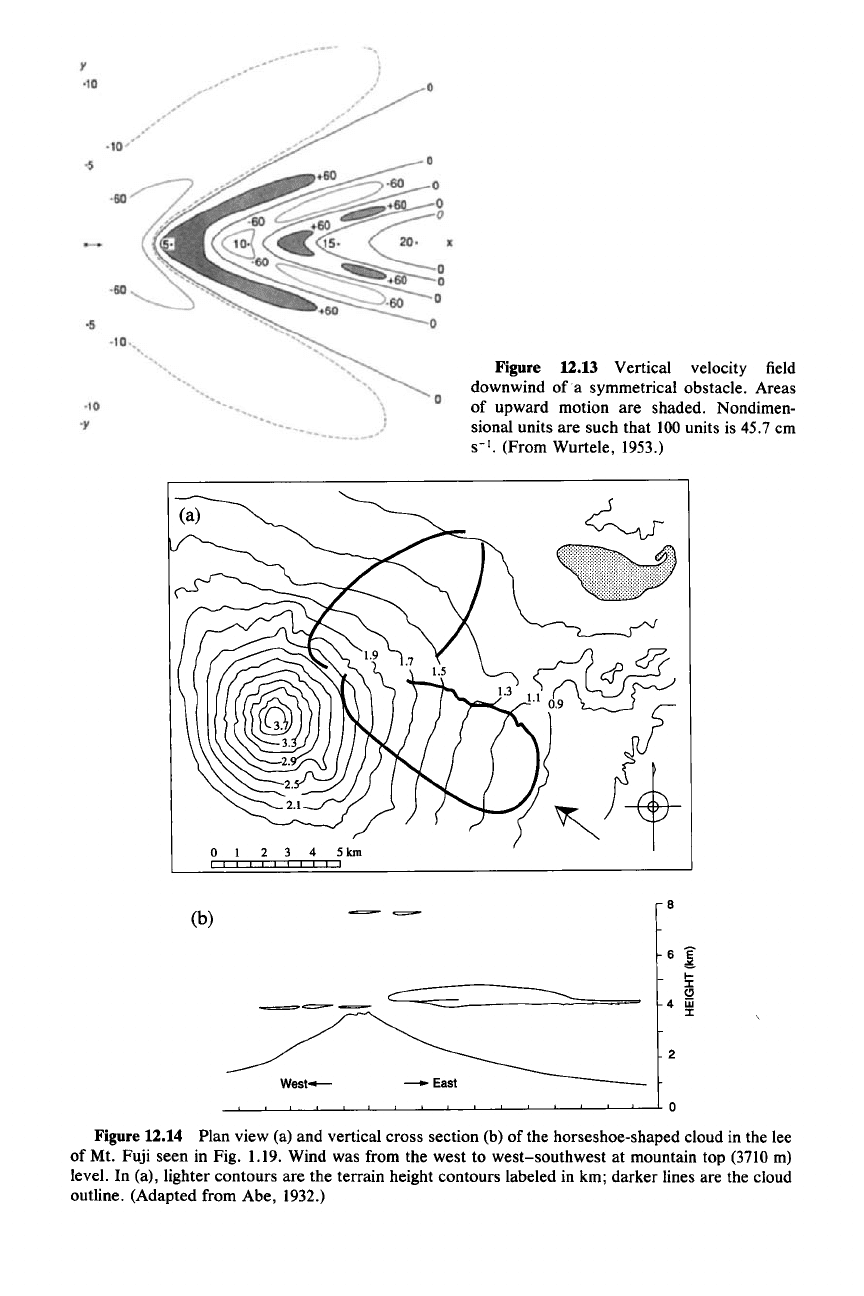
(a)

, I

(b)

2 3 4

5km

I I ! I I I I

Figure 12.13 Vertical velocity field

downwind

ofa

symmetrical obstacle. Areas

of upward motion are shaded. Nondimen-

sional units are such that 100units is 45.7 em

S-I.

(From Wurtele, 1953.)

West-

-East

Figure 12.14 Plan view (a) and vertical cross section (b) of the horseshoe-shaped cloud in the lee

of Mt. Fuji seen in Fig. 1.19. Wind was from the west to west-southwest at mountain top (3710 m)

level. In (a), lighter contours are the terrain height contours labeled in km; darker lines are the cloud

outline. (Adapted from Abe, 1932.)

524 12 Orographic Clouds

Figure 12.15

150

125100

-0

..-----0-

o 25 50 75

x (km)

O~O

0 0 4

~~()UU

Figure 12.16

Figure 12.17

12.3 Clouds Associated with Flow over Isolated Peaks 525

shown photographically in Fig. 1.19 was studied

and

mapped photogrammetri-

cally as

shown

in Fig. 12.14.

327

The

vertical motion field in Fig. 12.13 is

not

the only form

that

mountain waves,

and

hence

wave

clouds,

can

take

downstream

an isolated peak. So far we have

only

considered

the

simplified

case

constant

and

and hence

constant

£2.

The

wave

trapping

that

occurs

when

ii varies with height while

constant

has

been

studied-"

by examining

the

case

where

ii varies exponentially with height,

such

that

Ii =U e

(12.53)

where

the

mean

wind at

the

ground

and

t: is the wind scale height.

is found

that

even

a slight wind

shear

is associated with a considerable amount of trap-

ping.F?

The

trapped

waves

that

develop in

the

flow

past

a mountain peak are

analogous to

waves

produced

by a ship.

These

ship waves

appear

as distinct

modes

ofthe

solution to (12.48),

when

the

full expression (12.5) is used for

£2,

and

iizz

determined

from

(12.53).

These

modes

are

two distinct types, as illus-

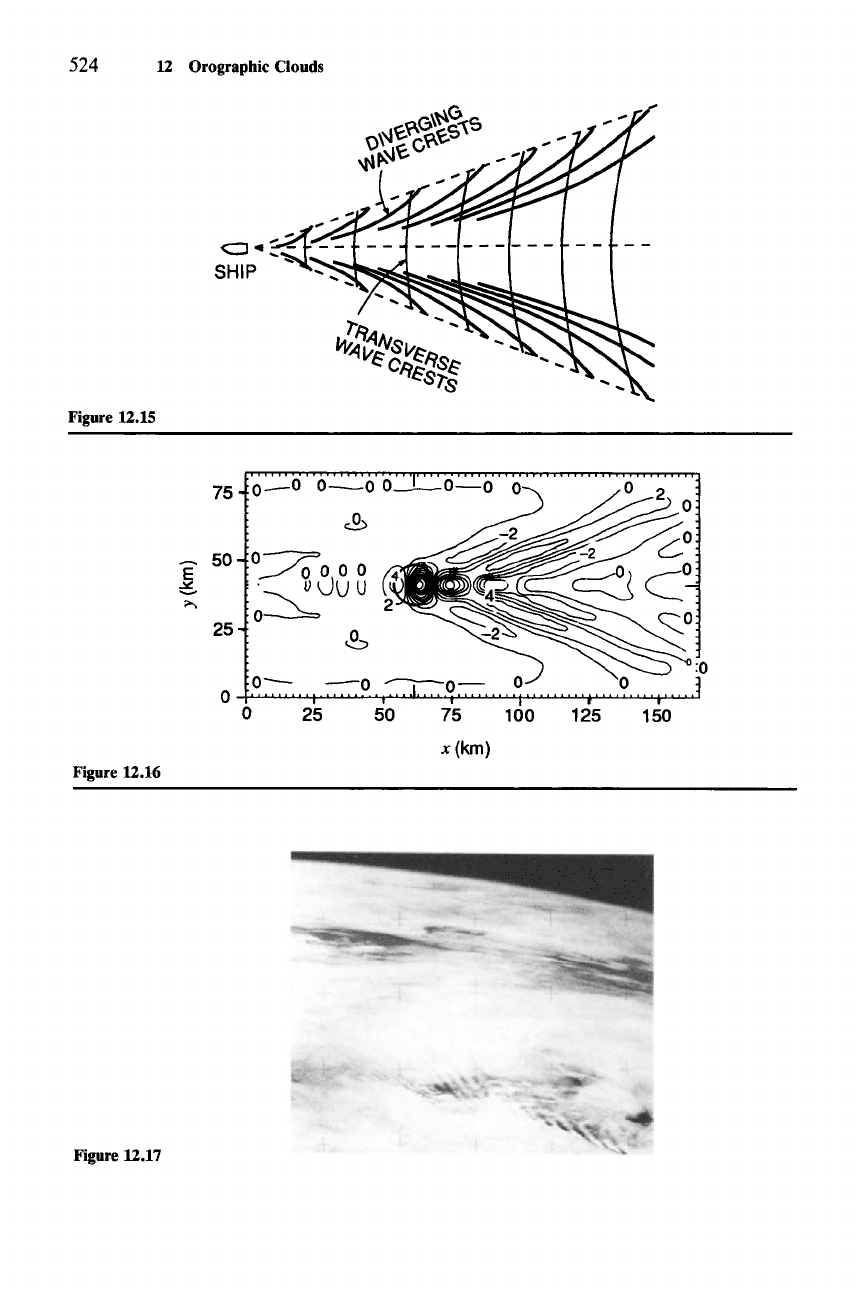
trated in Fig. 12.15.

Inside

a wedge-shaped

zone

downwind

the peak, there are

transverse

waves,

which

lie

less perpendicular to the basic-state flow, and

diverging

waves,

with

crests

that

meet

the

incoming flow at a small angle. Outside

the wedge, only diverging modes exist.

330

The

transverse

waves

are

analogous to the

trapped

lee waves that

occur

in two-

dimensional flow.

They

consist

superpositions

waves that have attempted to

327 The detailed photogrammetric study by Abe

(1932)

of a horseshoe-shaped cloud in the lee of Mt.

Fuji in Japan helped motivate Wurtele's (1957) study of the three-dimensional linear dynamics of the

flow over isolated three-dimensional mountain peaks. Wurtele's solution of (12.50), shown in Fig.

12.12, was meant to explain Abe's photographs.

328 By Sharman and Wurtele (1983).

329 This exponential representation of the wind actually has the property that £2

- L

-2

as z

00,

so that every wavelength is ultimately trapped.

330 For further discussion of these wave types, see Smith

(1979)

and Sharman and Wurtele

(1983).

Figure 12.15 Horizontal configuration of transverse and diverging phase lines for deep-water

"ship waves." (From Sharman and Wurtele, 1983. Research sponsored by NASA Dryden FRF,

L. J.

Ehernberger, monitor. Reprinted with permission from the American Meteorological Society.)

Figure 12.16 Numerical-model simulation of highly sheared flow over a 300-500-m-high obstacle.

Vertical velocity at the 5-km level is shown (in 2 cm

S-I

contour intervals) after the flow has reached a

steady state. Each tick mark on the frame enclosing the pattern indicates the location of a horizontal

grid point (2.5 km). The obstacle is centered at the long tick marks. The contour representing the

obstacle shape is shown as the heavy circle; the contour shown is the one for which the obstacle height

is 0.1 the maximum height. (From Sharman and Wurtele, 1983.Research sponsored by NASA Dryden

FRF,

J. Ehernberger, monitor. Reprinted with permission from the American Meteorological

Society.)

Figure 12.17 Example of clouds associated with diverging wave modes in the lee of Bouvet

Island. The photo was taken by

Skylab astronauts (photo reference number: SL4-137-3632). The exact

scale of the picture is not known. Numerical simulations of this type of wave structure suggest that the

crests are

-10-40

km apart.

526 12 Orographic Clouds

propagate upstream but have been advected to the lee. The diverging waves have

not attempted to propagate upstream but instead have propagated laterally away

from the mountain while being advected to the lee by the basic current. Numerical

model experiments for flow over a 300-500-m-high obstacle have been performed

with the full set of time-dependent equations for a range of wind shear, indicated

by the ratio

R =

Nil

U«, where N is given by (2.98). Since N is constant, the range

Ris determined entirely by the shear, as measured by the wind scale height L.

We will examine results, after the flow reaches a steady state, for three values

Results at low R (high shear) are shown in Fig. 12.16. Here only diverging

modes exist. Strong motions are organized in bands forming a pattern similar to

that of the idealized diverging wave crests in Fig. 12.15. The strong vertical

motions are concentrated on the edges of the wedge, with relatively little distur-

bance directly downstream of the mountain in the center of the wedge. Figure

12.17 shows an example of clouds associated with diverging wave modes.

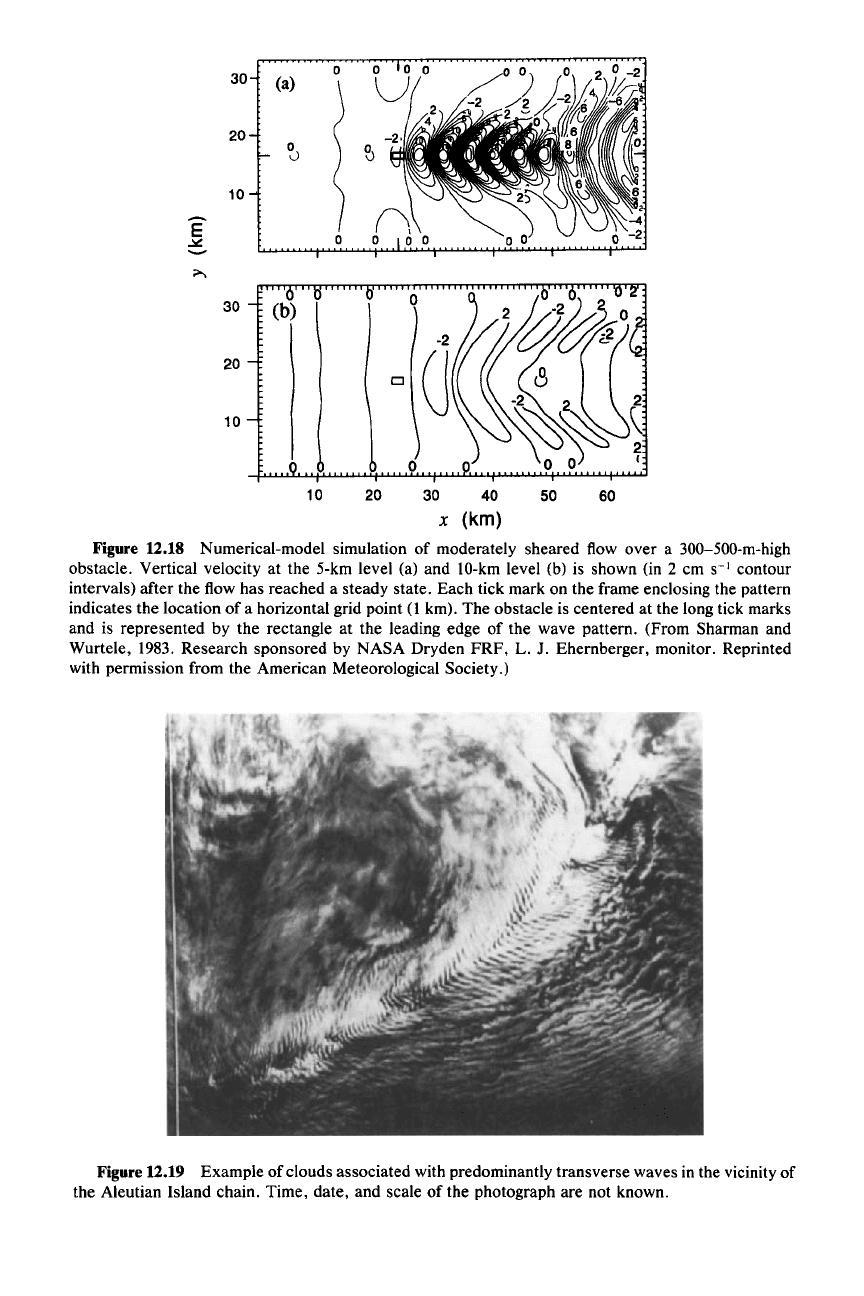
Figure 12.18 shows results at moderate

R. In this case, both types of waves

occur in the wedge-shaped region downwind of the mountain. Only diverging

waves exist outside the wedge. Response at this particular

R includes a strong

transverse pattern across the wedge. These waves turn into diverging structure

outside the wedge. The effect of trapping in the case of the transverse waves is

evident by the series of waves downstream, which resemble lee waves downwind

of a two-dimensional ridge, and by the fact that the wave amplitude rapidly dies

out with increasing altitude (cf. Fig. 12.18a and b). Figure 12.19 shows an example

of clouds associated with predominantly transverse waves.

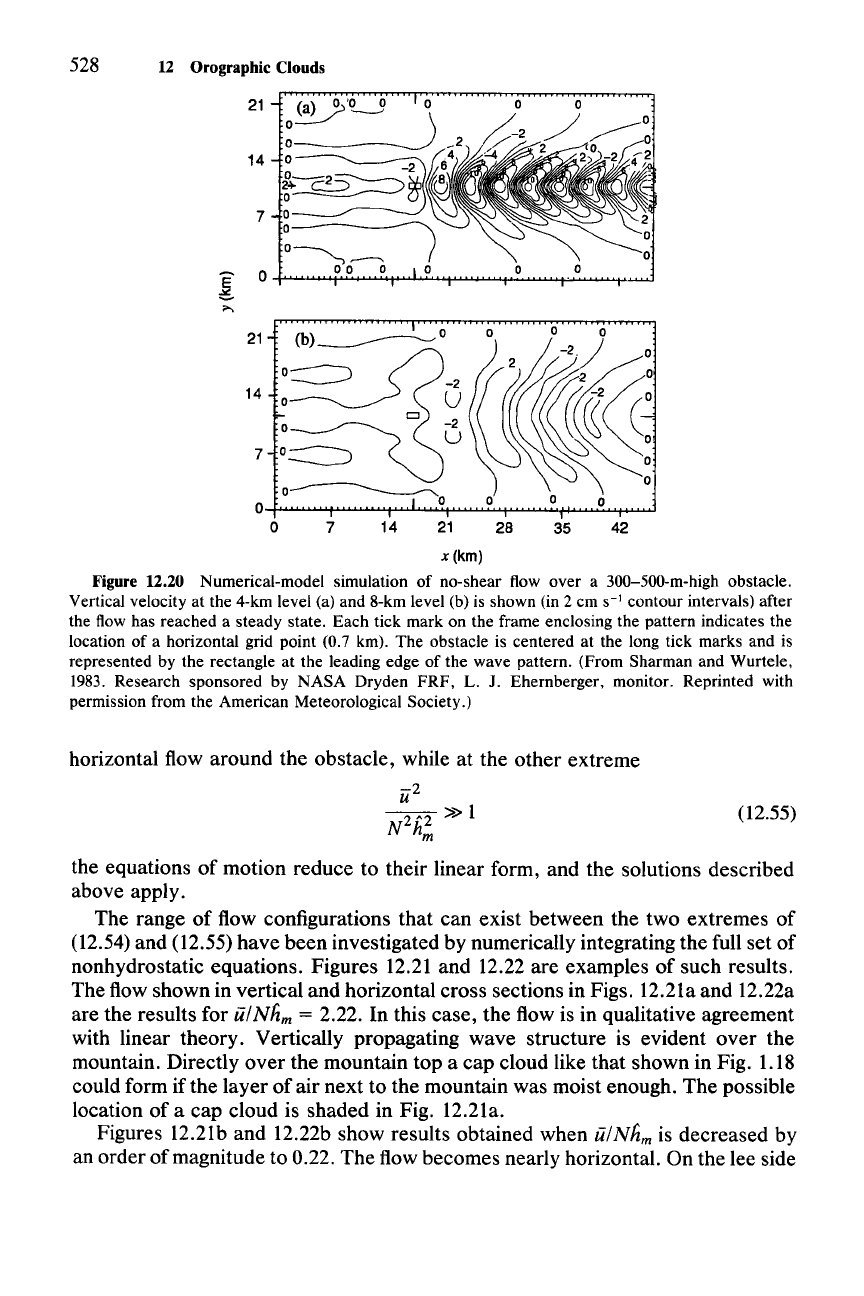
The case of infinite

R reduces to the no-shear

(if

= constant) case examined

previously. Figure 12.20illustrates this case, in which there is no trapping, and the

horseshoe-shaped vertical velocity pattern is again seen downwind. This pattern

is not readily distinguishable from that of moderate

R (cf. Fig. 12.18).

horse-

shoe-shaped clouds are observed to the lee of a mountain peak, they are probably

associated with trapped waves, since the calculations show that even small shear

produces significant trapping.

So far, we have considered only small-amplitude (linear) perturbations pro-

duced in flow over a three-dimensional mountain peak. In the two-dimensional

case, we saw that in the case of shallow-water flow over an obstacle of finite

height, the flow is blocked whenever

[defined by (12.29)] is sufficiently small.

A similar tendency is found in continuously stratified fluid if

A2 « 1 (12.54)

N h

where h

is the maximum height of the mountain. The condition (12.54) is met if

the fluid is either moving slowly, extremely buoyantly stable, or both. If the

obstacle is a three-dimensional peak, rather than a two-dimensional ridge, then

instead of being blocked, the flow turns laterally and finds a way around the

mountain.

can be shown''" that in the case of (12.54)the flow reduces to a purely

331 See Durran (1990) for further discussion and references.

(a)

;>-,

6050

2010 30 40

x (km)

Figure

U.18

Numerical-model simulation of moderately sheared flow over a 300-500-m-high

obstacle. Vertical velocity at the 5-km level (a) and 10-km level (b) is shown (in 2 em

S-I

contour

intervals) after the flow has reached a steady state. Each tick mark on the frame enclosing the pattern

indicates the location of a horizontal grid point

km). The obstacle is centered at the long tick marks

and is represented by the rectangle at the leading edge of the wave pattern. (From Sharman and

Wurtele, 1983. Research sponsored by NASA Dryden FRF,

L. J. Ehernberger, monitor. Reprinted

with permission from the American Meteorological Society.)

Figure

U.19

Example of clouds associated with predominantly transverse waves in the vicinity of

the Aleutian Island chain. Time, date, and scale of the photograph are not known.

528

Orographic Clouds

..,

O-f'-'~""""'t~~'t"'-'-'.L..u4""~.u:.....t'""'"'-~"T'-'''''''''';'4..............J

o 7 14 21 28 35 42

x (km)

Figure 12.20 Numerical-model simulation of no-shear flow over a 300-500-m-high obstacle.

Vertical velocity at the 4-km level (a) and 8-km level (b) is shown (in 2 em

S-l

contour intervals) after

the flow has reached a steady state. Each tick mark on the frame enclosing the pattern indicates the

location of a horizontal grid point (0.7 km). The obstacle is centered at the long tick marks and is

represented by the rectangle at the leading edge of the wave pattern. (From Sharman and Wurtele,

1983. Research sponsored by NASA Dryden

FRF,

L. J. Ehernberger, monitor. Reprinted with

permission from the American Meteorological Society.)

(12.55)

horizontal flow around the obstacle, while at the other extreme

2'T»

N h

the equations of motion reduce to their linear form, and the solutions described

above apply.

The range of flow configurations that can exist between the two extremes of

(12.54) and (12.55)have been investigated by numerically integrating the full set of

nonhydrostatic equations. Figures 12.21 and 12.22 are examples of such results.

The flow shown in vertical and horizontal cross sections in Figs. 12.21aand 12.22a

are the results for

iii

ss:

= 2.22. In this case, the flow is in qualitative agreement

with linear theory. Vertically propagating wave structure is evident over the

mountain. Directly over the mountain top a cap cloud like that shown in Fig. 1.18

could form if the layer of air next to the mountain was moist enough. The possible

location of a cap cloud is shaded in Fig. 12.21a.

Figures 12.21b and 12.22b show results obtained when

iilNh.

is decreased by

an order of magnitude to 0.22. The flow becomes nearly horizontal. On the lee side