Houze Robert A., Jr. Cloud Dynamics

Подождите немного. Документ загружается.

(7.96)

7.5 Modeling of Convective Clouds

259

-r

......

--t---h....,..--rz

= 0

r=R

r=O

r=R

Figure 7.26 Representation of thermal-like air motions near cloud top in a one-dimensional cloud

model of radius R. The thermal circulation is assumed to be a sphere located within the dashed outline.

The level tangent to the top of the sphere

(Z,) is cloud top. The base of the thermal is at level ZL.

Triangular curves show the assumed radial distributions of vertical velocity as a function of height z.

Note that the triangularity of the updraft profiles increases with height only in the thermal cap region.

(From Ferrier and Houze, 1989. Reproduced with permission from the American Meteorological

Society.)

To obtain this particular form, we have taken the base-state density and pressure

to be

Pe and

respectively. We have further made use of the assumptions that

u, = 0 and that p, does not vary in the horizontal to write U = u, = u* and ap*/ar =

ape/ar. Integrating (7.95) from r = R to an arbitrary radius r

in the cloud, we

obtain

r' D u*

(r') =

(R) - P

dr'

R Dt

Ifthe

environmental pressure Pe is subtracted from both sides, an average is taken

over the area of the cloud, and circular symmetry

(a/a® = 0) is assumed, the

above becomes

= 2

[f~

Du*(r)

]

(p*)

= P* - P

R Dt dr

(7.97)

The value of u*(r) is obtained by substituting the triangular vertical velocity profile

w,(r) into the continuity equation and integrating from the center of the cloud to r.

Thus, the model prediction of vertical velocity implies a prediction of u* that must

be consistent in terms of mass continuity. This prediction of u* in turn implies the

mean in-cloud pressure perturbation according to (7.97).

Results obtained with a one-dimensional time-dependent model of the type

described above are shown in Fig. 7.27 for an environment characteristic of a

convective region over a tropical ocean. The cloud was initiated by maintaining a

6050

(d)<B>

16r-------------------,

16 (f)

«p

40 50 60

3020

(e)<qL>

16,-------------------,

(a)<W>

(b)<

....

.02

(g) 1

d<P>

10 20

.05

30 40

TIME

(minutes)

:I:

ill

:I:

.01

TIME

(minutes)

7.5 Modeling of Convective Clouds

261

vertical velocity forcing of w = 2 m

S-1

at the

O.4-km

level for 20 min. The

categories of water included in (7.94) were vapor, cloud liquid water, and rainwa-

ter [as defined in (3.48)]. The sources and sinks were formulated according to the

warm-cloud bulk water-continuity scheme described in Sec. 3.6.1.

194

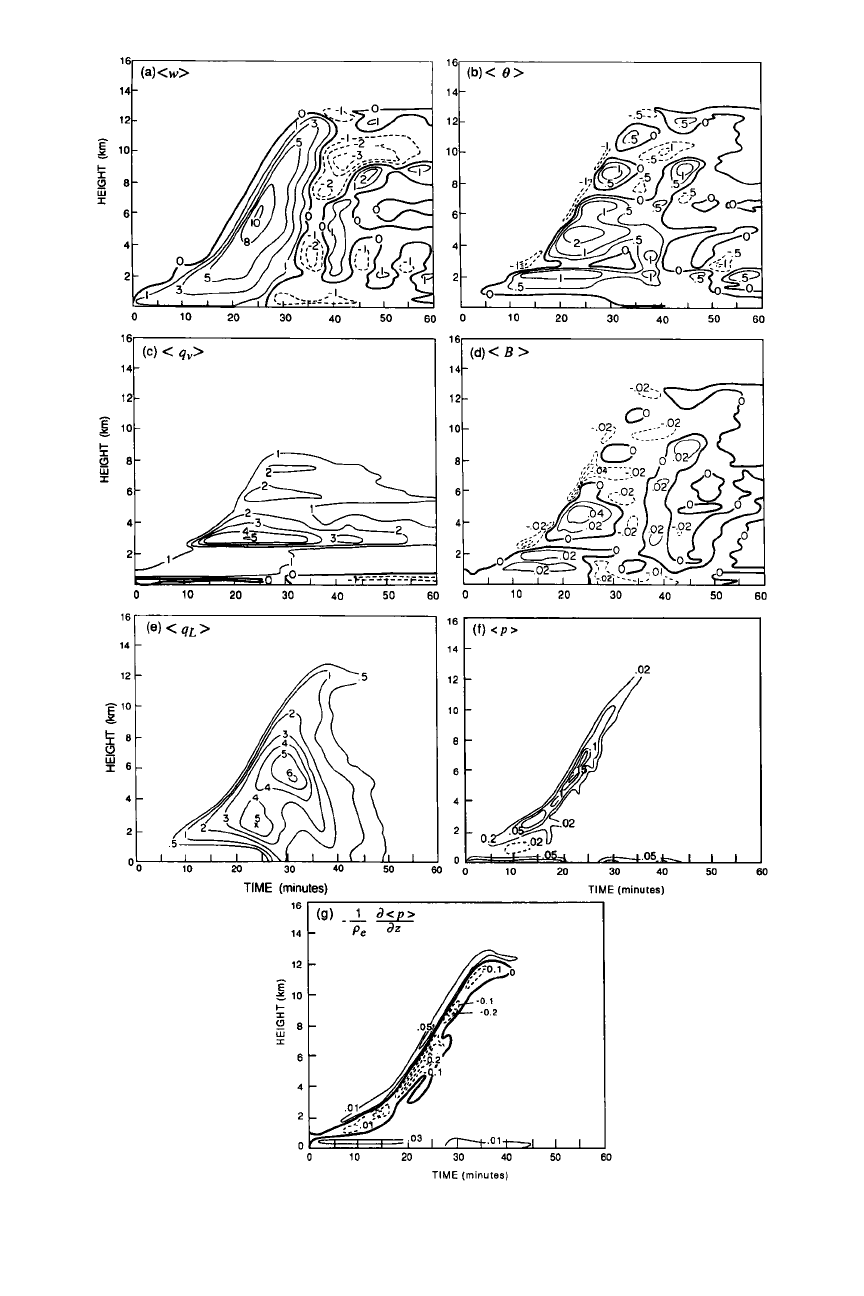
From all the panels of Fig. 7.27, it can be seen that the model cloud grew

steadily for 30-35 min, reaching a maximum altitude of 13

krn. During most of this

growth period, the cloud consisted of updraft at all levels, with the strongest

upward motion in the middle levels of the cloud (Fig. 7.27a). In the growing

updraft, the perturbations of potential temperature and water-vapor mixing ratio

were generally positive (Fig. 7.27b and c), contributing to positive buoyancy (Fig.

7.27d). As the liquid water content increased (Fig. 7.27e), the buoyancy was

weakened as a result of the weight of the hydrometeors [recall term

qH in (2.50)].

This negative buoyancy reversed the vertical velocity. Downdraft first formed at

low levels, where the liquid water content first became large (7.27a). Eventually it

was felt at higher and higher levels, following the zone of maximum liquid water

content, which also was found at progressively higher levels. After 40 min, weak

updraft returned after the water had mostly fallen out as precipitation. After 35-40

min, the model cloud structure is probably not very realistic.

The pressure perturbation in the model cloud is most noticeable at the earth's

surface and at cloud top (Fig. 7.270.

For

the first 20 min, the positive pressure

perturbation at the surface was required to support the imposed updraft forcing at

cloud base. The positive perturbation at low levels after 25 min was associated

with the downdraft, which had to decelerate as it approached the ground. The

positive pressure perturbation at cloud top is associated with the rising buoyant

overturning thermal located there. The pressure-gradient acceleration associated

with the thermal (Fig. 7.27g) is consistent with the idealized case illustrated in Fig.

7.1. As in the idealized case, the buoyancy gradient across the top of the cloud

requires upward force above the parcel to push the environmental air out of the

way of the cloud top. Model experiments verify that without this upward force

above the cloud (a condition that can be produced by setting the pressure pertur-

bation to zero), the cloud is unable to reach realistic heights. The downward

pressure-gradient acceleration

just

below cloud top is the resistance felt by the

parcel as buoyancy forces it upward. This resistance has the effect of smoothing

the vertical profile of vertical velocity, since it slows the rising air down more

gently in the upper reaches of the cloud than would be the case in the absence of

pressure perturbation.

194

For

further details about how the calculation was set up, see Ferrier and Houze

(1989).

Figure 7.27 Results of a one-dimensional time-dependent model for an environment characteristic

of conditions over a tropical ocean. (a) Vertical velocity in m

S-I.

(b) Potential temperature

perturbation in "C. (c) Water-vapor mixing ratio perturbation in g kg-I. (d) Buoyancy acceleration in m

S-2.

(e) Liquid water mixing ratio in g kg-I.

(f)

Pressure perturbation in mb. (g) Vertical acceleration

owing to the vertical gradient of pressure perturbation (m

S-2).

(From Ferrier and Houze, 1989.

Reproduced with permission from the American Meteorological Society.)

262 7 Cumulus Dynamics

7.5.3 Two- and Three-Dimensional Models

We have seen that one-dimensional Lagrangian and one-dimensional, time-depen-

dent cumulus models illustrate some of the basic features of buoyancy, entrain-

ment, and pressure perturbation. They also provide some interesting qualitative

results and constitute rather quick and easy methods for estimating the convective

response in a given thermodynamic environment.J" On the other hand, they are

highly parameterized, such that they obscure all the horizontal motions in clouds,

and they reveal nothing about the effects of the wind in the environment on the

convection. In view

our discussion of the development of vertical vorticity in

convective clouds (Sec. 7.4), the shear of the wind in the environment of a con-

vective cloud would seem to be quite important to the development of the cloud.

Not only do vortical motions develop in response to the wind, but these vortical

motions effect important feedbacks. The vorticity induces entrainment, which

alters the thermal and moisture structure of the cloud and, hence, the buoyancy

and vertical motion. The stronger vortices also produce dynamically induced

pressure perturbations [through term

FD in (7.4)], the gradients of which strongly

affect certain convective storms. To include these additional effects, it is neces-

sary to construct two- and three-dimensional convective cloud models, which can

predict accurately the horizontal as well as the vertical air motions in clouds.

In two- and three-dimensional cumulus models there are no

a priori specified

cloud boundaries, as there are in the one-dimensional models. Instead, a wind

field is calculated in some larger spatial domain from initial fields of wind and

thermodynamic variables. Within this model domain, clouds form whenever and

wherever the predicted motions dictate.

Two- and three-dimensional cumulus models require no arbitrary assumptions

about entrainment since the horizontal and vertical air motions outside and inside

the cloud are resolved down to the scale of the finite-difference grid of the model.

Entrainment and detrainment are automatically accounted for as air flows in and

out of clouds according to the overall predicted motion field. Standard turbulence

parameterizations are used to account for mixing on scales smaller than the model

grid. In the terminology of the previous subsection, dynamic entrainment

(~I)

specifically resolved, while entrainment produced by lateral eddy mixing

(~2)

and

vertical eddy fluxes

(~3)

are accounted for by the parameterization of subgrid-

scale turbulence.

Models are said to be two-dimensional if variations in one horizontal direction

are assumed to be zero. If, in a rectangular Cartesian framework, variations in the

y-direction are set to zero and motions are computed in the

x-z

plane, the model is

referred to as

slab-symmetric. This type of geometry is sometimes useful for

representing convective clouds at a front or along a squall line. If, in a cylindrical

coordinate system centered on a vertical axis, variations in the azimuthal direc-

tion are set to zero and motions are computed in a radial plane, the model is called

195 Note that only a temperature and humidity sounding of the environment is required as input to

the one-dimensional models.

7.5 Modeling of Convective Clouds

263

axially

symmetric.

This type of geometry can be useful for representing the

flow

a circular vortex, such as a hurricane.

Two-dimensional models are based on the combination of the vertical equation

of motion with one of the horizontal component equations of motion, for example,

the x-component. To solve the x-component equation for the perturbation of

velocity from a basic-state environment, the initial value of the wind in the

direction must be provided throughout the model domain. Often this is the large-

scale environment motion

u; measured by standard soundings. The initial thermo-

dynamic state of the environment must be similarly provided. Evidently, since

only one component of the environmental wind is an input parameter, the only

situations that can be well represented by a two-dimensional model are those in

which the shear of the wind is unidirectional. This limitation of two-dimensional

models is severe, and consequently the three-dimensional model is the more

important tool. Nonetheless, there are a few cloud systems for which a two-

dimensional model can be useful.

Two-dimensional slab-symmetric motions in a vertical plane have the interest-

ing characteristic that they are governed entirely by the very simple vorticity

equation (2.61), in which the only forcing for the two-dimensional motions is the

horizontal gradient of buoyancy

•

The vorticity equation can be solved for g

simultaneously with the thermodynamic and water-continuity equations, for the

motions that follow from an initial perturbation of the buoyancy and/or wind field

somewhere within the model domain. As shown in Sec. 5.3.4, the vorticity

g can

in turn be related through mass continuity to the velocity components

U and w via

a stream function. A two-dimensional vorticity equation in stream function form

can also be derived for an axially symmetric model. This strategy of obtaining the

two-dimensional velocity field avoids having to calculate the pressure perturba-

tion field. However, sometimes it is desirable to know the pressure perturbation

field and this technique does not provide it. Also, the stream function method is

not readily extended to three-dimensional calculations. Another strategy for two-

dimensional modeling is to simplify a three-dimensional model by setting horizon-

tal derivatives in one direction to zero. If a three-dimensional model is available,

this is the easier strategy to employ and has the advantage of providing the

pressure perturbation field associated with the air motions.

Three-dimensional models are formed by combining all three components of

the equation of motion (2.47) with the thermodynamic and water-continuity equa-

tions. Advection terms in

x, y, and z are all included in

Dt.

Initial values of both

components of the horizontal wind are specified everywhere within the model

domain. If atmospheric sounding data are used as input, both components of the

environmental horizontal wind are used along with the measurements of the ther-

modynamic state

ofthe

environment. Thus, all of the information contained in the

sounding data is utilized, and the model air motions can form and evolve in

response to an environment characterized by wind that varies in both direction

and speed with altitude. Such a model is necessary to represent complex convec-

tive phenomena such as tornadic thunderstorms, which form in highly sheared

environments (Chapter 8).

264 7 Cumulus Dynamics

One type of three-dimensional convective model is based on the anelastic

equations. The first three-dimensional models were of this type.

196 In this type of

cloud model, the mean variable versions of the vector equation of motion (2.83),

thermodynamic equation (2.78), water-continuity equations (2.81), equation of

state (2.73), and continuity equation (2.75) are solved simultaneously for a pre-

scribed initial disturbance placed somewhere in the model domain. The pressure

perturbation is calculated from a diagnostic equation similar to (7.4). This equa-

tion is obtained by taking

. Po (2.83) and making use of the mean-variable anelas-

tic continuity equation (2.75). The result is

p* =

+ P

(7.98)

where FBand FD are similar to their counterparts in (7.4), except that here they are

computed from the mean-variable values of buoyancy and wind, and

FM is the

density-weighted divergence

(V'

. Po) of the turbulent eddy-mixing terms that ap-

pear in (2.83).

Results obtained from this type of model are illustrated in Fig. 7.28 and are

from one of the first articles reporting results of three-dimensional modeling. The

categories of water included in (2.81) were vapor, cloud liquid water, and rainwa-

ter. The warm-cloud bulk parameterization scheme described in Sec. 3.6.1 was

used to relate these categories of water to one another. The model domain was

38.4 km in the

x- and y-directions and 15 km in the vertical. The environment was

represented by a sounding that was conditionally unstable (Sec. 2.9.1) below 5 km

altitude. The relative humidity was between 80 and 100% up to 1.2 km, then

decreased to 30% at 10.2 km and remained at this value up to 15 km. The environ-

mental wind profile was assumed to be unidirectional, varying linearly from

-6

6 m

S-1

between 0.3 and 8.1 km and constant above and below these levels. An

initial thermal perturbation was imposed on this environment.

consisted of a

region 7.4 km in horizontal diameter and 1.2 km deep centered at an altitude of 1.5

km. The magnitude of the temperature perturbation at the center was assumed to

be 0.3°C.

The structure of the model cumulonimbus cloud that evolved from this pertur-

bation is shown in its mature stage in Fig. 7.28. Panel (a) is a vertical cross section

along the

y = 19.2 km line in the horizontal plane shown in panels (b)-(d). This

vertical cross section shows an updraft and downdraft coexisting. The updraft

slopes up and over the denser downdraft, which is located in the region of precipi-

tation reaching the surface. The downdraft air can be seen flowing in from the rear

at middle levels and running under the updraft. The spreading out of the down-

draft air at low levels can be seen in plan view in Fig. 7.28b. At middle levels (Fig.

7.28c), the counter-rotating vortices formed by tilting of the environmental hori-

zontal vorticity are seen straddling the updraft, as expected from the discussion of

Fig. 7.23 in Sec. 7.4.3. This vortex pair entrains air into the downdraft on the

downwind side of the storm, and middle-level environmental air splits and flows

around the vortex pair. A distinctly diffluent and divergent outflow is seen near

196 See, for example, Wilhelmson (1974), Schlesinger (1975), and Clark (1979).

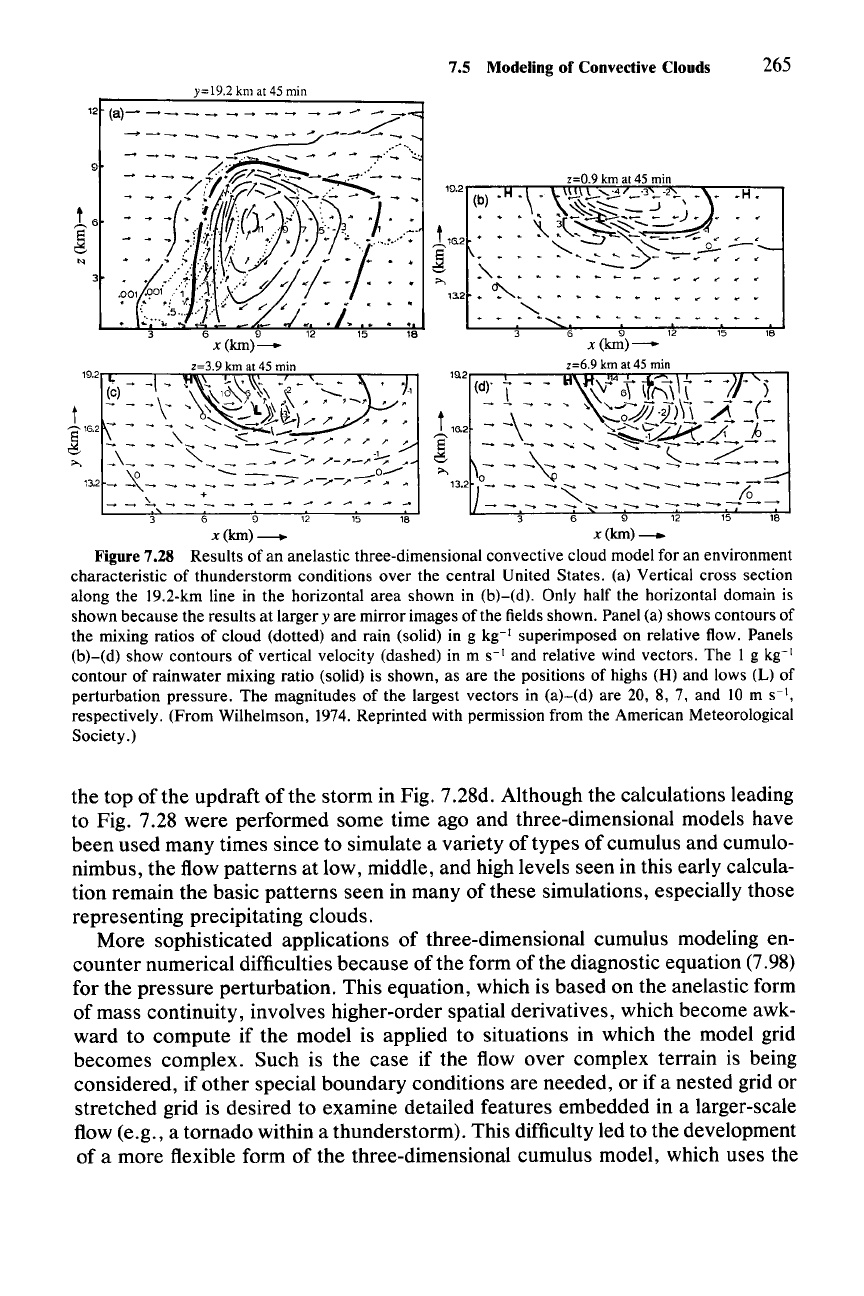
7.5 Modeling of Convective Clouds 265

1512

z=0.9km at 45 min

(b) • •

~3:/_,.

.H.

;r,---~

:.--)

'''~'-2r-''',,=--

..::-'

.. .. .. .. ..

'_"'"-::,:)-

-;::-.;;

.. of

.....

- - - -

,..,

13.2

t 16.2

y=19.2 km at 45 min

t 6

the top of the updraft

ofthe

storm in Fig. 7.28d. Although the calculations leading

to Fig. 7.28 were performed some time ago and three-dimensional models have

been used many times since to simulate a variety of types of cumulus and cumulo-

nimbus, the flow patterns at low, middle, and high levels seen in this early calcula-

tion remain the basic patterns seen in many of these simulations, especially those

representing precipitating clouds.

More sophisticated applications of three-dimensional cumulus modeling en-

counter numerical difficulties because of the form of the diagnostic equation (7.98)

for the pressure perturbation. This equation, which is based on the anelastic form

of mass continuity, involves higher-order spatial derivatives, which become awk-

ward to compute if the model is applied to situations in which the model grid

becomes complex. Such is the case if the flow over complex terrain is being

considered, if other special boundary conditions are needed, or if a nested grid or

stretched grid is desired to examine detailed features embedded in a larger-scale

flow (e.g., a tornado within a thunderstorm). This difficulty led to the development

of a more flexible form of the three-dimensional cumulus model, which uses the

Figure

7.28

Results of an anelastic three-dimensional convective cloud model for an environment

characteristic of thunderstorm conditions over the central United States. (a) Vertical cross section

along the 19.2-km line in the horizontal area shown

(b)-(d). Only half the horizontal domain is

shown because the results at larger

are mirror images

the fields shown. Panel (a) shows contours

the mixing ratios of cloud (dotted) and rain (solid) in

kg-'

superimposed on relative flow. Panels

(b)-(d) show contours of vertical velocity (dashed) in m

s-'

and relative wind vectors. The

kg-'

contour of rainwater mixing ratio (solid) is shown, as are the positions

highs

(H)

and lows

(L)

perturbation pressure. The magnitudes

the largest vectors in (a)-(d) are

20,

7, and

s-I,

respectively. (From Wilhelmson, 1974. Reprinted with permission from the American Meteorological

Society.)

266 7 Cumulus Dynamics

fully compressible mass continuity equation (2.20) rather than the anelastic form

(2.54).

The difficulties with the model based on the anelastic form are purely numeri-

cal. The anelastic equations remain an excellent approximation of the governing

dynamics of cumulus convection. The only consequence of using the continuity

equation in anelastic form is that sound waves are filtered out of solutions to the

model equations. These waves are of no interest in convective cloud dynamics. If

uncontrolled numerically, they can obscure the solutions of interest. Therefore,

the anelastic equations would seem desirable. Unfortunately, the awkward form

of (7.98) severely limits their utility in numerical modeling. In the fully compress-

ible equations [i.e., when a prognostic equation for the pressure perturbation

based on (2.20) is used in place

ofthis

diagnostic relation (7.98)], all of the wind,

thermodynamic, and water-continuity variables are obtained from prognostic

equations of a similar form, and the numerical difficulties associated with (7.98)

are removed from the model. The sound waves are retained in the equations but

are controlled by a numerical technique called "splitting," in which the sound

wave modes are solved for separately, using a shorter time step than used else-

where in the model."? Thus, three-dimensional convective cloud models have

been developed in which the fully compressible rather than the anelastic equations

are integrated numerically. This type of model has been extremely successful in

simulating and yielding insight into the dynamics of severe thunderstorms, espe-

cially tornadic storms and squall line thunderstorms. The dynamics of thunder-

storms described in Chapter 8 have been largely learned from studies of numerical

simulations of storms carried out with fully compressible three-dimensional nu-

merical models. The same type of model has been used with great success to

simulate the convection in the eyewalls of hurricanes (Chapter 10), clouds along

cold fronts (Chapter 11), and mountain waves (Chapter 12).

A further degree of sophistication employed in some three-dimensional convec-

tive cloud models is in the parameterization of the subgrid-scale turbulence. The

mixing coefficients for all of the variables are considered to be functions of the

subgrid-scale eddy kinetic energy

'J[, The eddy kinetic energy equation (2.86) is

introduced as an additional prognostic equation, which is solved simultaneously

with the three component equations of motion, the prognostic pressure perturba-

tion equation, the thermodynamic equation, and the water-continuity equations.

In this way, the subgrid-scale turbulence is computed in a way that is internally

consistent with all of the other variables that are predicted.

198 To solve the kinetic

energy equation along with the other prognostic equations, expressions for the

terms on the right-hand side of (2.86) must be found. One way these terms have

been expressed is as follows: (i) The pressure-velocity correlation term

ignored. (ii) The eddy fluxes contained in the definitions of

Cf6

and

[(2.88) and

197 See Klemp and Wilhelmson (l978b) for details.

198 The type of model in which pressure perturbation and eddy kinetic energy are included as

prognostic variables was introduced by Klemp and Wilhelmson (l978a) and is often referred to as the

Klemp-

Wilhelmson model.

7.5 Modeling of Convective Clouds

267

(2.89)] are parameterized in terms of K-theory with mixing coefficients K

as in

(2.185). According to this parameterization, the mixing coefficients are related to

'J( according to the "inertial subrange" turbulence parameterization.!" in which

oc £G'j{1/2 (7.99)

where

is the cube root of the grid volume and serves as a length scale. (iii) The

dissipation

'2lJ

is also expressed according to this parameterization, as

'2lJ

£G-1'j{3/2 (7.100)

Since the mixing terms in all the prognostic equations are parameterized as func-

tions of mixing coefficients, which are functions of

'j{, and since 'j{ is predicted in a

way that is internally consistent with the other predicted variables, the vertical

and lateral eddy mixing components of entrainment are able to evolve in a way

that is consistent with all the model variables.

199 See Klemp and Wilhelmson (l978a), Deardorff (1972), and Schemm and Lipps (1976).

Chapter

8 Thunderstorms

...

in the mad thunder-cloud, as when

Fierce legions clash

...

" 200

The previous chapter considered certain dynamical aspects that are basic to all

convective clouds. Buoyancy, pressure perturbation, entrainment, and cloud vor-

ticity were introduced and examined, and we noted how these dynamics are

incorporated into cloud models. In this chapter, we focus specifically on one type

of convective

cloud-the

cumulonimbus, or thunderstorm cloud. As noted in

Chapter 1, cumulonimbus can occur either in isolation (Sec. 1.2.2.1) or as part of

large mesoscale convective systems (Sec. 1.3.1). The next chapter of this book is

devoted entirely to the structure and dynamics of mesoscale convective systems.

Here we will concentrate on the properties of isolated thunderstorms and lines of

thunderstorms. An understanding of individual storms and lines is crucial because

they are important weather-producing phenomena in their own right and because

they are building blocks of the larger mesoscale systems.

The isolated cumulonimbus is one of the most visually striking and photogenic

of all cloud phenomena. The visual appearance of these clouds was illustrated by

Figs. 1.4 and 1.5. In this chapter, however, we are not concerned so much with

the exterior appearance of these clouds as with their internal structure and dy-

namics. We will begin by examining small, isolated cumulonimbus (Sec. 8.1).

Then we will consider larger isolated thunderstorms, which are divided into two

categories referred to as multicell and supercell thunderstorms (Sees.

8.2-8.6). In

Sees,

8.8-8.10, we will examine three important circulation features of large

thunderstorms: tornadoes,

gustfronts,

and downbursts. Finally, in Sec. 8.11, we

will consider the conditions that favor the grouping of individual thunderstorms

into lines

storms.

8.1 Small Cumulonimbus Clouds

is possible for a warm cumulus cloud (i.e., one with no ice in it) to precipitate

and hence to be classified as cumulonimbus. Such small precipitating cumuliform

clouds are common in the tropics. However, most cumulonimbus clouds contain

200 Goethe's reference to a thunderstorm.

268