Houze Robert A., Jr. Cloud Dynamics

Подождите немного. Документ загружается.

7.4 Vorticity 249

clouds become tilted out of the horizontal, some of the rotation is about a vertical

axis. This vertical component of vorticity can become quite concentrated and is

manifested most strongly in funnel clouds, waterspouts, and tornadoes.

While it is, of course, possible to view the fluid motions in convective clouds in

terms of pressure gradients and buoyancy in the context of the equation of motion

(7.2), the presence of vortical motions in clouds makes it enticing to examine the

air motions via the vorticity equations (2.58) and (2.59), which eliminate the

pressure-gradient terms and address the rotation directly in terms of the buoyancy

source. In this section, we will examine briefly the development of vorticity in

convective clouds in terms of the horizontal and vertical vorticity equations. Here

we will introduce some basic concepts, which will be applied further and elabo-

rated on in later chapters concerned with thunderstorms and mesoscale convec-

tive systems.

7.4.2 Horizontal Vorticity

The generation of horizontal vorticity

in a two-dimensional Boussinesq fluid is

governed by (2.61), which says that the only way that vorticity about a horizontal

axis can develop within a two-dimensional parcel

air is through a horizontal

gradient

buoyancy Ex (i.e., by baroclinic generation). In the case of convective

clouds, the primary situations in which

is generated baroclinically are illustrated

in Fig. 7.22. The case

ofthe

positively buoyant rising element that overturns like a

Hill's vortex (Sec. 7.3.2) is represented in Fig. 7.22a. In this case, a maximum of

positive buoyancy is centered in the element, so that

Ex is of equal magnitude and

Figure 7.18 Paluch diagram showing aircraft measurements (small crosses) and environmental

sounding data (heavy solid line) for a real cumulus cloud in which air from cloud base (heavy cross)

mixes in various fractions with air entrained from near flight level (about

570 mb). (From Austin et al.,

1985. Reprinted with permission from the American Meteorological Society.)

Figure 7.19 Paluch diagram of the total water mixing ratio

qr(

= q, + qc) and "equivalent potential

temperature"

(6,) for an idealized aircraft flight in a cumulus cloud in which the parcels of air

encountered at flight level are mixtures of cloud-base air and environmental air entrained at a

multiplicity of altitudes and balloon ascent in the environment. Cloud top is determined by the rise of

the few

"lucky"

undiluted parcels.

Figure 7.20 Paluch diagram showing aircraft measurements (small crosses) and environmental

sounding data (heavy solid line) for a real cumulus cloud in which the parcels of air encountered at

flight level are mixtures of air from cloud base (heavy cross) and environmental air entrained at a

multiplicity of altitudes. (From Taylor,

1987.)

Figure 7.21 Cumulus cloud conceptualized as consisting of a collection of parcels that each

undergo mixing with entrained air at one and only one level. Equal parcels are considered to be

released from cloud base to each of several discrete levels above cloud base

(i,j,

etc.). Upon reaching a

designated level, each parcel is split into several subparcels, each mixing with a different fraction of

environmental air. Cloud top is determined by the rise of the few

"lucky"

undiluted parcels. (Based on

Raymond and Blyth,

1986.)

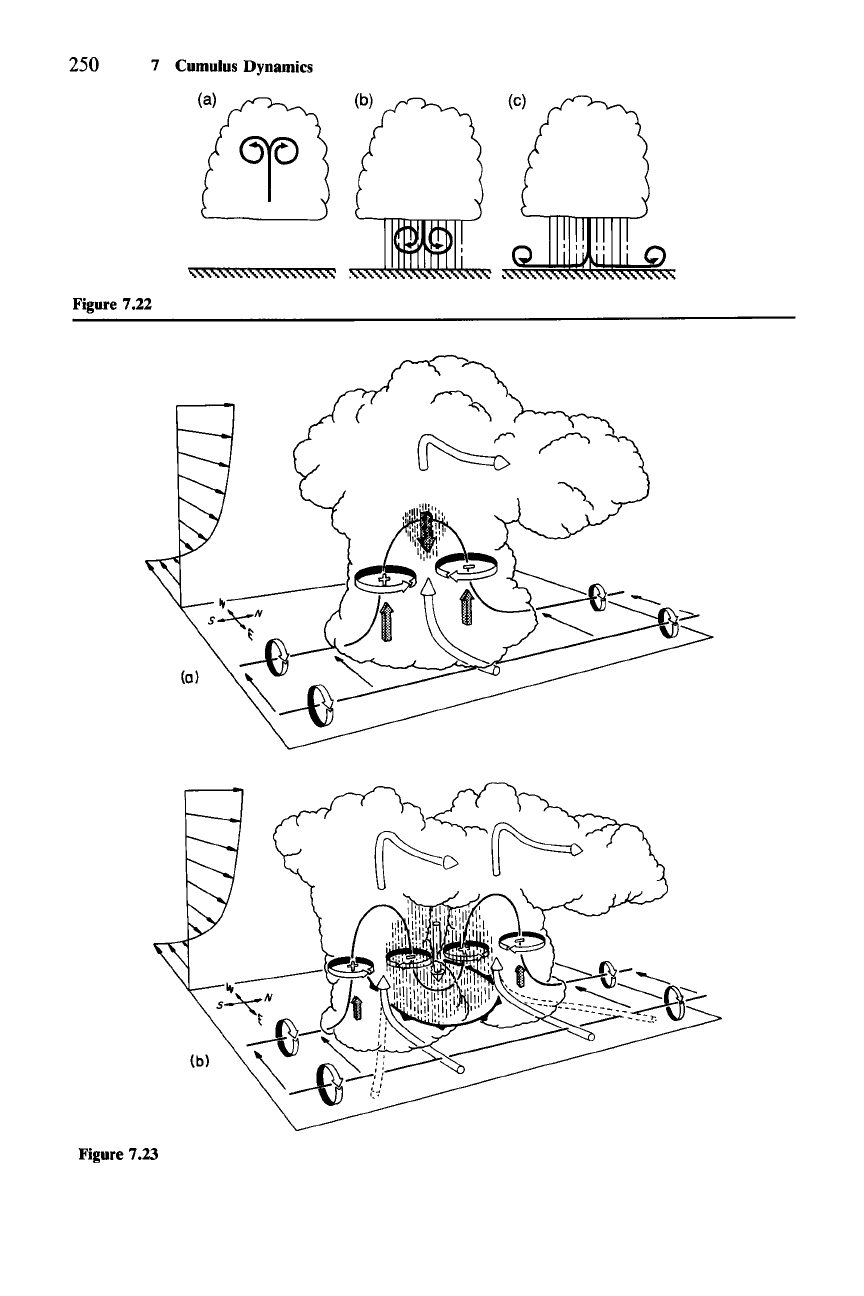
250 7 Cumulus Dynamics

Figure 7.22

(b)

Figure 7.23

7.4 Vorticity

251

opposite sign on either side of the center line of the element. Counter-rotating

vortices are thus produced on either side of the cloud. These vortices are entirely

consistent with the buoyancy pressure gradient force field associated with the

motions (Fig. 7.1). The case of a negatively buoyant downdraft associated with

evaporative cooling and precipitation drag in the rain shower of a convective

cloud is illustrated in Fig. 7.22b.

is the upside-down version of the overturning

updraft. A maximum of negative buoyancy is centered in the element, so that

B, is

again of equal magnitude and opposite sign on either side of the element, and

counter-rotating vortices are again produced. As a downdraft of dense air spreads

out along the ground, a strong buoyancy gradient and vortex is maintained at the

leading edge of the outflow (Fig. 7.22c).

7.4.3 Vertical Vorticity

On the basis of numerical modeling and observations by Doppler radar of severe

thunderstorms, it is now generally agreed that intense vorticity about a vertical

axis

(0 in convective clouds has its origin as horizontal vorticity. One way that

the vertical vorticity in cloud arises is by converting horizontal vorticity of the

environment to vertical vorticity in cloud. This process of conversion is easily

envisaged by considering a large-scale environment in which the mean flow

ii is

unidirectional in the x-direction and increasing with height. Then the environment

has horizontal vorticity whose value is the shear

aii/az. This vorticity is illustrated

schematically by the north-south-aligned vortex tubes outside the cloud in Fig.

7.23a. When the updraft of the convective cloud is superimposed on the vortex

tube, the tube is deformed upward such that there then exists vorticity around

vertical axes in the form of counter-rotating vortices on either side of the updraft

core.

This intuitive picture is formalized by ignoring the Coriolis force, which is

negligible on the cumulus scale, and linearizing the vertical vorticity equation

Figure 7.22 Generation of horizontal vorticity by horizontal buoyancy gradients. (a) Positively

buoyant updraft. (b) Negatively buoyant downdraft in rain. (c) Spreading of negatively buoyant

downdraft along the earth's surface.

Figure 7.23 Conversion of horizontal vorticity of the environment to vertical vorticity in cloud.

Mean environmental flow

ii (shown by thin arrows) is unidirectional in the x-direction and increasing

with height. Horizontal vorticity of the environment is indicated by the north-south-aligned vortex

tubes outside the cloud. Shaded arrows represent the forcings that promote new updraft and downdraft

growth. Rain is shown by vertical hatching. Cylindrical arrows show the direction of cloud-relative

airflow. Heavy solid lines represent vortex lines with the sense of rotation indicated by circular

arrows. (a) Linear tilting of the environmental horizontal vorticity by cloud vertical air motion leads to

the indicated vertical vorticity couplet. (b) Splitting of the storm as a result of nonlinear effects.

Frontal symbol at the surface marks the boundary of the cold air spreading out beneath the storm.

Dashed cylindrical arrows indicate shifted location of the storm inflow when updrafts become

established on the storm flanks. (From Klemp, 1987. Reproduced with permission from Annual

Reviews, Inc.)

252 7 Cumulus Dynamics

(2.59) about the mean flow v = (u,0,0).187 In this case we obtain the perturbation

form of the equation

(7.68)

we consider a level where uapproximates the velocity of the cloud relative to

the ground, (7.68) becomes

(7.69)

in a system moving with the cloud. Thus, tilting of the vortex tubes of the mean-

flow shear is the only important source of perturbation vorticity

In the case

shown in Fig. 7.23a, this process leads to positive " on the south side of the

updraft and negative

r on the north side of the updraft.

Numerical models and Doppler radar data confirm that linear tilting of the

environmental horizontal vorticity is an important mechanism for the formation of

vertical vorticity in convective clouds that form in environments of substantial

shear (large

z).188

The r couplet shown in Fig. 7.23a is indeed a characteristic of

the early stage of convection that develops in shear. The counter-rotating "

couplet, among other things, constitutes a mechanism of entrainment. In the case

shown in Fig. 7.23a, the vortices would draw environmental air into the east side

of the storm at midlevels. Our previous discussion of entrainment (Sec. 7.3)

considered only those entrainment processes that would occur in an environment

without shear.

is evident from the present discussion that entrainment in con-

vective clouds in strongly sheared environments will be enhanced as a result of

the vortex couplet straddling the updraft.

As clouds develop beyond the stage illustrated in Fig. 7.23a, nonlinear effects

become important. These effects have also been inferred from numerical-model-

ing results.

189

has been found that the perturbation vorticity equation becomes

(7.70)

The difference from (7.68) is that now stretching

(rw

)

is important in addition to

tilting. The regions oflarge

IWzl

at the tops and bottoms of the convective updrafts

and downdrafts are especially conducive to strong vortex stretching.

Processes that occur during the later phases of cumulonimbus development will

be discussed in Chapter 8.

For

reasons to be discussed there, we will see that a

severe thunderstorm in an environment of strong unidirectional shear, like that

depicted in Fig. 7.23a, splits in half, with the two halves moving in opposite

directions along the y-axis, as indicated in Fig. 7.23b. The cloud motion relative to

the ground at this stage of storm development may then be represented by

(7.71)

\87 The mathematical arguments and deductions from numerical-model results presented in this

subsection are from Rotunno (1981) and the review article of Klemp (1987).

\88 See the review of Klemp (1987).

189 Ibid.

7.5 Modeling of Convective Clouds

253

At the level of nondivergence, uis found to be approximately equal to

u.,

Model

results show that the only significant terms in the linearized perturbation form of

the vorticity equation (2.59) at the level of nondivergence in a coordinate system

moving with the cloud, with Coriolis effect neglected, are

(7.72)

(7.73)

Under steady-state conditions,

-~w

Thus, the maximum of " coincides with the maximum w, and the southward-

moving storm produced by the split has positive vorticity whenever

ii,

In this

way, a rotating updraft can develop in midlevels in severe thunderstorms. Such a

rotating updraft is called a

mesocyclone and is the main part of the storm in which

intense tornadoes form. Tornadic thunderstorms will be considered in more detail

in Chapter 8.

The above discussion indicates how vertical vorticity can arise in convective

clouds by conversion of horizontal vorticity of the environment to in-cloud verti-

cal vorticity. In Sec. 7.4.2 we noted how concentrated horizontal vorticity is

generated by the cloud itself, especially at the edges of downdraft outflows (Fig.

7.22c). This cloud-generated horizontal vorticity can also sometimes be tilted into

the vertical. Conversion of the cloud-generated horizontal vorticity can indeed be

extremely important. We will see in Chapter 8 that the main tornado in a supercell

thunderstorm forms

at the

gust

front, Because the convergence at the gust front is

so strong, the fully nonlinear form of the vertical vorticity equation (2.59) applies.

The Coriolis force remains unimportant, but both tilting and stretching are impor-

tant along the gust front. The horizontal vorticity generated by the strong buoy-

ancy gradient across the gust front is advected horizontally into the center of the

storm and tilted by the convective updraft and, at the same time, concentrated

into an intense local vortex by the strong convergence at the base of the updraft.

This strong vortex is a favorable environment in which a funnel cloud or tornado

can form. These processes will be examined further in Chapter 8.

7.5 Modeling of Convective Clouds

7.5.1 General Considerations

In Sec. 7.3.2, we saw that by following a single entraining parcel of in-cloud air

upward, we could estimate the properties of the rising parcel along its path by

means of the closed set of equations constituting the one-dimensional Lagrangian

cumulus model. In the special case of a steady-state cloud, where a series of

identical parcels rise one after the other, that type of calculation also describes the

properties of the cloud as a function of height. The Lagrangian model, however, is

inadequate for a full description of the properties of a convective cloud in space

254 7 Cumulus Dynamics

and time. The need for a more complete description is acute. Radar, aircraft,

satellite, and other special observational platforms can be employed to observe

the detailed structure and evolution

certain fields in developing clouds (such as

the wind and radar reflectivity). These observational technologies can be ex-

tended by methods such as the retrieval technique described in Sec. 4.4.7 to

diagnose variables beyond those which can be observed directly. However, it is

impossible with any foreseeable technology to observe or diagnose all of the

thermodynamic, kinematic, and water fields simultaneously in a developing cumu-

lus or cumulonimbus cloud with the spatial and the temporal resolution required

to understand the cloud physics and dynamics. As a substitute for a complete set

of observations, the science of convective cloud modeling is employed to calcu-

late the relevant fields simultaneously in a physically consistent way from first

principles. By seeking agreement of the model results with the few fields that are

observed, one can then use the model output to extend the understanding of the

clouds. In the following subsections, we summarize how the basic equations are

organized to formulate the basic types of convective cloud models that are in use.

The goal is to familiarize the reader with the physical basis of the models. We

make no attempt to review problems related to numerical solutions, as this topic

would fill a book by itself.

7.5.2 One-Dimensional Time-Dependent Model

The first type of model we will examine is the one-dimensional time-dependent

model.

190

is simplified in that it predicts only the horizontally averaged proper-

ties in cloud. However, these properties are computed as functions of time, thus

providing an indication

the cloud's evolution. The computed variables are

considered to be deviations from environmental values. If

slc represents the in-

cloud value of any quantity

sl,

then

slc =sle+

* (7.74)

The model is formulated in cylindrical coordinates

(r,8,Z),

and the cloud region is

specified a priori to have a radius

R(z).

A horizontal average over the cloud is

given by

\sl)

f2/r

cAr

while the average along the outer boundary of the cloud is

12/r

cA= -

cA(R,e)de

(7.75)

(7.76)

190 This type of model has appeared in the literature in several forms. The version described here

was proposed by Asai and Kasahara (1967).

was further developed by Ogura and Takahashi (1971)

and Scott and Hobbs (1977), who combined the dynamical equations of Asai and Kasahara with water-

continuity schemes that included ice-phase microphysical processes. Ferrier and Houze (1989) added

several modifications to the dynamical formulation, including new ways of representing entrainment

and pressure perturbation. The discussion in this section is based mostly on their version.

7.5 Modeling of Convective Clouds 255

The deviation from the

area

average of

.stl

* will, for simplicity, be written as

.stl':

.stl*

(.stl*

) (7.77)

Strictly, it should be written as

(.stl*)'.

The deviation from the boundary average is

.stl":

.stl*(R,

-.stl * (7.78)

(7.79)

(7.80)

The area-averaged continuity equation is obtained by applying (7.75) to the an-

elastic continuity equation (2.54) written in cylindrical coordinates with the den-

sity weighting factor taken to be the environmental density

Pe. The result is

(-=

dR) 1 d ( 2 (

*))

- u - w - +

---

PeR

w = 0

PeR2

where u

and

ware

the velocity components in the radial and vertical directions,

respectively.

The

first term is the horizontal inflow required to balance the vertical

gradient of mass flux contained in the second term. The second term in the first

parentheses is the component of inflow

that

arises if the volume containing the

cloud has nonvertical sides.

For

example, the radius at low levels might be speci-

fied to contract with height (Fig. 7.24b), or at high levels the cloud volume might

be assumed to

expand

in radius with height.

The

total derivative of an in-cloud variable in cylindrical coordinates can be

written with

the

aid

(2.54) as

D.stl

d.stl

dId

* 1 d ( * )

c =

c +

--(ru*.stl

) +

--;-(.stl

v ) + --=:;-

Pew

.stl

Dt at r dr r

where v is the velocity component in the azimuthal direction. The environment

has

been

assumed to be motionless

(u,

= v, =

= 0). If (7.80) is multiplied by

and (7.75) is applied to it, we obtain the horizontally averaged equation

where

[

dR)](( *)

-*)

<&1

= R u - W

a;-

.stl

2(-

-aR)

<&2

= - R u"

.stl"

w".stl"

a;-

(7.82)

(7.83)

(7.84)

1 d

---(p.

w'.stl'))

In obtaining (7.81)-(7.84), we made use of the continuity equation (7.79) and the

identity,

(W*.stl*)

(W*)(.stl*)

+ (w'.stl')

(7.85)

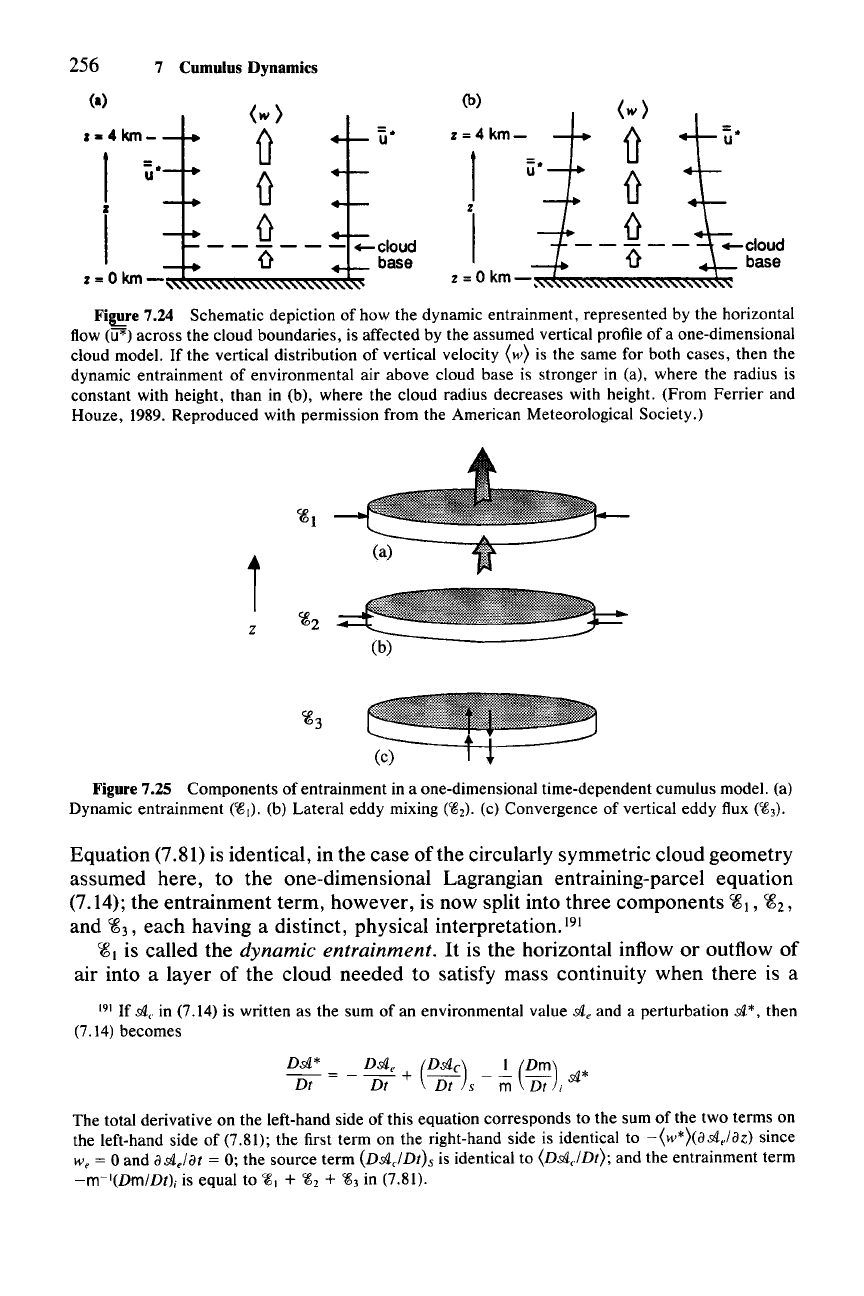
256

Cumulus Dynamics

(a)

(w>

(b)

(w)

,.4km-

u·

z=4km-

u·

{)

_cloud

{)

--0---

base

--0--

km-

Fi~re

7.24 Schematic depiction of how the dynamic entrainment, represented by the horizontal

flow

(ifI') across the cloud boundaries, is affected by the assumed vertical profile of a one-dimensional

cloud model.

Ifthe

vertical distribution of vertical velocity (w) is the same for both cases, then the

dynamic entrainment of environmental air above cloud base is stronger in (a), where the radius is

constant with height, than in (b), where the cloud radius decreases with height. (From Ferrier and

Houze, 1989. Reproduced with permission from the American Meteorological Society.)

";gl

Figure 7.25 Components of entrainment in a one-dimensional time-dependent cumulus model. (a)

Dynamic entrainment

(~I)'

(b) Lateral eddy mixing

(~2)'

(~3)'

Equation (7.81) is identical, in the case

ofthe

circularly symmetric cloud geometry

assumed here, to the one-dimensional Lagrangian entraining-parcel equation

(7.14); the entrainment term, however, is now split into three components

~l,

~2,

and

~3,

each having a distinct, physical interpretation. 191

is called the dynamic entrainment.

is the horizontal inflow or outflow of

air into a layer of the cloud needed to satisfy mass continuity when there is a

191 If

.sI1.

in (7.14) is written as the sum of an environmental value

.sI1.

and a perturbation

.sI1.*,

then

(7.14) becomes

D.sI1.*

= _

D.sI1.

(D.sI1.

-.!-

(Dm)

.sI1.*

Dt Dt Dt s m Dt i

The total derivative on the left-hand side of this equation corresponds to the sum of the two terms on

the left-hand side of (7.81); the first term on the right-hand side is identical to

-(w*)(a.sl1.,Iaz) since

We = 0 and

a.sl1.

efat

= 0; the source term

(D.sI1.c1Dt)s

is identical to

(D.sI1.,JDt);

and the entrainment term

-m-I(DmlDtli

is equal to

in (7.81).

7.5 Modeling of Convective Clouds

257

vertical gradient of vertical mass flux across the layer (Fig. 7.25a). It is assumed

that

.cA*

is zero when there is inflow and is equal to the in-cloud average

(.cA*)

when

there is outflow.

Thus,

'i8

dilutes the cloud when entrainment is occurring, but is

zero when detrainment occurs. Dynamic entrainment is a strong effect in this type

of model and is not independent of the assumed model geometry. Figure 7.24

shows how the same vertical distribution of vertical velocity

(w*) has less inflow

and hence less dilution of in-cloud properties when the model domain is wider at

low levels.

is indeed a weakness of this type of model that the shape of the

domain can determine whether or not the cloud will form and what its internal

properties will be. One must be careful to specify a realistic shape for the domain

if this type of model is to be useful.

'i8

is the lateral eddy mixing, which is the turbulent mixing of air across the

boundary without a net exchange of mass across the cell boundaries (Fig. 7.25b).

There is observational evidence that the lateral mixing is smaller than vertical

mixing.

192 In addition, dimensional arguments have often been invoked to indicate

that

(7.86)

(7.89)

where ai is a positive constant with a magnitude of about 0.1.

193

This value proves

to be considerably smaller than the dynamic entrainment or vertical mixing. Thus,

'i8

appears to be the least important of the three components of entrainment and

perhaps entirely negligible.

'i8

is the convergence

the vertical eddy flux across the top and bottom of an

infinitesimal layer of cloud (Fig. 7.25c). For this term, it is necessary to express

(w'.cA')

in meaningful physical terms. In early modeling this term was at times

ignored, assumed to be implicitly accounted for by numerical smoothing or repre-

sented by simple diffusive mixing. None of these approaches turn out to be satis-

factory. Somewhat better results are obtained with the following scheme, inspired

by the observation that the top of a growing cumulus cloud has the form of an

overturning vortex ring (Sec. 7.3.2, Figs. 7.8-7.10) and that cumulus updrafts and

downdrafts tend to have triangular profiles of variables, with a peak in the center

of the draft and dropping off to a minimum on the edge of the draft. These

observations can be represented by letting

.cA

# (7.87)

where

.cAr(r)

is the basic triangular radial distribution of sl"; and

.cA#

represents a

smaller-scale, turbulent fluctuation about the basic triangular profile. If the

smaller-scale fluctuations are random, then we also have

(w*.cA*)

= (Wr(r).silr(r)) + (w#.sil#) (7.88)

with the assumed triangular profiles

= (w*)j(r),

.sil

= (.cA*)g(r)

192 See discussion and references in Ferrier and Houze (1989).

193 See Asai and Kasahara (1967)or Ogura and Takahashi (1971)for a discussion of the dimensional

argument.

258 7 Cumulus Dynamics

Thus

(w*dl*)

XA(w*)(dl*)+(w#dl#)

where

is a constant. Combining this expression with (7.85), we obtain

(7.90)

(7.91)

Thus, the vertical eddy flux has been decomposed into a part associated with the

basic triangular variation of

dl* across the cloud (first term on the right) and a part

arising from the smaller-scale turbulence (second term on the right). The latter is

of secondary importance in the convergence of vertical eddy flux on the right-

hand side of (7.84). Its effect can be estimated by a K-theory parameterization.

The first term on the right of (7.91) becomes very important in (7.84) near cloud

top, where it can be designed to simulate the behavior of an overturning thermal.

This technique is illustrated in Fig. 7.26, where it can be seen that the triangular

profile of

w* across the cloud is arranged and prescribed in such a way that there is

a thermal cap region (enclosed by the circle)

just

below cloud top. From the height

of the center of the thermal cap upward into the region

just

above cloud top z., the

value of

w* at cloud edge is negative, while it remains positive in the center of the

draft.

The vertical profile of horizontally averaged variables in cloud is computed

from prognostic equations of the form (7.81) for vertical velocity, potential tem-

perature, and a set of water-substance mixing ratios. The forcing functions

(Vdlcl

Vt)

for these variables are obtained by applying (7.75) to the right-hand sides of

(7.1), (2.9), and (2.21) over the area of the cloud. The results are, respectively,

(

)

1 a/

- =

---\p

+ (B)

Dt P

(0;;

(oJe)

(7.92)

(7.93)

and

(7.94)

(7.95)

The base-state density

has been taken to be the large-scale environment value

Pe,

'if

is the net heating resulting from phase changes associated with the micro-

physical processes incorporated in the

S, terms, and n is the number of categories

of water substance represented by the in-cloud mixing ratios

qic'

The horizontally averaged pressure perturbation (p*) in (7.92) can be obtained

diagnostically from other equations. From Sec. 7.2, we recall that the pressure

perturbation is implied by mass continuity together with the horizontal and verti-

cal equations of motion. In the present context, the horizontal component of the

equation of motion (2.47) may be written as

Du*

aPe

=---