Houze Robert A., Jr. Cloud Dynamics

Подождите немного. Документ загружается.

6.4 Radiation and Turbulent Mixing in Nimbostratus

219

modynamic equation (2.78) in this case may be written as

Dt =

'1Jf

'1Jf/

'1Jf

(6.2)

where the terms on the right represent latent heating

(~d

associated with phase

changes (condensation, evaporation, deposition, sublimation, melting, freezing),

infrared heating

(~I)'

solar heating

(~s),

and the redistribution of heating by

turbulent mixing

('leT

_p;;lV·

Pov'fJ'). The turbulent mixing was determined as

an adjustment of the temperature lapse rate in the cloud, which was assumed to be

saturated. Wherever the lapse rate becomes potentially unstable

(afJel

az < 0) in a

model time step, the temperature distribution with respect to height was im-

mediately restored to neutrality

(afJelaz

= 0).

'leT

is effectively the heating or

cooling implied by the restoration process. The eddy flux convergence was in-

cluded in the water-continuity equations with a K-theory formulation (Sec. 2.10.1)

in which the value of

K was chosen to be that which would produce an amount of

mixing consistent with the convective adjustment

~T'

Two-dimensional (no

y-variation) versions of the thermodynamic and water-continuity equations were

integrated in time until steady-state fields were obtained within the nimbostratus

region of a mesoscale convective system similar to that depicted in Fig. 6.12. Air

motions in the nimbostratus were given by observations and held constant at their

observed values during the integration.

The horizontally averaged steady-state values of the terms in (6.2) obtained in

the integration are shown in Fig. 6.17. The cloud base was at the 4-km level, which

was also the

O°C

level, while the cloud top was at about 13 km. Under both

nighttime (Fig. 6.17a) and daytime (Fig. 6.17b) conditions, the primary diabatic-

heating effect through most of the cloud layer is the latent heating associated with

vapor deposition on ice. Below cloud base, melting and evaporation produce

cooling, which destabilizes a shallow subcloud layer. The convective overturning

that restores the lapse rate produces a shallow stratus layer, which accounts for

the net warming between 2 and 3 km.

During nighttime (Fig. 6.17a), infrared radiation cools the top

2.5 km of the

deep nimbostratus layer. This cooling destabilizes this upper layer, and turbulent

convective overturning acts to restore the lapse rate by warming the top 1 km of

the cloud above 12-km altitude and cooling a I.S-km-deep layer immediately

Figure 6.14 The steady-state distributions of mixing ratios of (a) snow q" (b) graupel qg, and (c)

rainwater

qr in a numerical simulation of a stratiform region associated with deep convection located

immediately to the right of the domain of the calculations. Units are g kg-I. (From Rutledge and

Houze, 1987. Reprinted with permission from the American Meteorological Society.)

Figure 6.15 As in Fig. 6.14 except for (a) rain rate (mm h-

and (b) radar reflectivity (dBZ). (From

Rutledge and Houze, 1987. Reprinted with permission from the American Meteorological Society.)

Figure 6.16 As in Fig. 6.14 except for (a) depositional growth rate of less dense snow, (b)

depositional growth rate of more dense snow, (c) melting rate, and (d) rate of evaporation of rain. Units

are 10-

g kg-I

S-I.

(Courtesy of S. A. Rutledge.)

220 6 Nimbostratus

Day

......

Night

12 (a)

0 0 0 -

Turbulent

In!rared

./'

.. " f."

0 0 8 0

mixing

°o~

.".

E 8

I-

a 6

(b) . )

.......

12 In!rared

_.:::

. 0

- Solar

.........

0'"

Turbulent

I \ /

mixing \I!\

!f <,

......

I \

:r I

Latent heal

./·:0

Turbulent

(

00% mixing

~"O'eo~r·o

OOOO~J>'::>

o 0

~-:'-:-:-::'-:-7-:--:-::'=-'.\~:

'-:-'=-----:"-:---='":----!"_=__'

-1.0 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1.0 -1.0 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1.0

Walls

I kg Walls I kg

Figure 6.17 Horizontally averaged steady-state diabatic heating terms in a model of nimbostratus

associated with deep convection. (a) Nightime, (b) daytime. (From Churchill and Houze,

1991.

Reprinted with permission from the American Meteorological Society.)

below 12 km. Thus, the top layer of the deep nimbostratus becomes a radiatively

driven mixed layer. However, it is at such a high and cold altitude that it does not

produce a significant amount of snow with which to seed the lower regions of the

cloud. The primary source of snow remains in the deep convection in the region

adjacent to the nimbostratus (Fig. 6.12).

is possible that in nimbostratus clouds

with lower tops, the radiative destabilization might have a more significant effect

on precipitation.

During the day (Fig. 6.17b), with a solar zenith angle of 30°, the diabatic heating

processes and profiles in the nimbostratus are similar to those during the night,

except for the effect of the solar radiation, which is felt in the upper portion of the

cloud. Although the short-wavelength absorption is strongest at upper levels, it

extends downward much farther than the infrared cooling. The solar heating is a

significant heat source throughout the upper

4-5

km of the nimbostratus layer.

Despite the solar heating, the infrared cooling remains strong enough to destabi-

lize the very top layer of cloud, and some convective overturning is present at

cloud top even under these daytime conditions.

Chapter

Cumulus

Dynamics

...

soaring, as if some celestial call

lmpell'd it to yon heaven's sublimest

hall:"!"

Clouds that occur when air becomes highly buoyant and accelerates upward in a

localized region

(~O.l-l

0 km horizontal extent) are referred to as convective or

cumuliform clouds. Included in this group are both cumulus and cumulonimbus,

which differ sharply from the stratiform clouds considered in Chapters 5 and 6,

not only in their visual appearance (Chapter

1) but also in their dynamics and

microphysics. Their vertical air motions are much stronger, and they condense

and precipitate water more intensely. They all have the appearance of rapidly

bubbling or

"soaring"

upward as they develop.

Cumuliform clouds exhibit a spectrum of forms, which include

• Fair weather cumulus, which are

I km in both horizontal and vertical

scale (e.g., the cumulus humilis in Fig. 1.3a).

• Cumulus congestus (towering cumulus), which attain widths and depths of

several kilometers as aggregates of discrete smaller buoyant bubbles within

the cloud rise one after the other, reaching successively greater heights (Fig.

1.3b, Fig. l.4a).

• Individual cumulonimbus (thunderstorms), which precipitate heavily, ex-

hibit lightning and thunder, produce strong outflow winds and tornadoes,

have widths of the order of tens of kilometers, and extend vertically to the

tropopause, where their tops spread out and form the characteristic anvil, or

thunderhead (Fig. l.4d, Fig. 1.5, Fig. 1.6).

• Mesoscale convective systems (complexes of thunderstorms), which have

cloud tops that extend over regions of the order of hundreds of kilometers in

scale, produce large amounts of rain, contain stratiform precipitation that

forms in connection with the cumulonimbus, and develop mesoscale circu-

lation patterns in addition to the convective-scale air motions (Fig. 1.27).

This spectrum of convective cloud phenomena may be thought of as represent-

ing the relative vigor and extent

ofthe

air motions associated with the clouds. The

underlying cloud dynamics are the dynamics of buoyant air; the air motions in all

convective clouds originate in the form of vertical accelerations that occur when

moist air becomes locally less dense than air in the surrounding larger-scale envi-

166 Goethe's words to describe a cumulus cloud.

221

222 7 Cumulus Dynamics

ronment. The accelerations associated with this buoyancy lead to vertical air

speeds

-1-10

S-I

and to several important dynamical and physical phenomena

that are associated with rapid local ascent and descent of air. First

all, as

parcels of air accelerate, the mass field in and around the cloud must adjust, and a

distinctive pressure field is required to accomplish this adjustment. Other phe-

nomena accompanying the buoyancy-driven vertical motions include the evolu-

tion of large liquid water content, produced by the rapid lifting, and consequent

growth of hydrometeors by accretion of liquid water (recall Sec. 6.1.1 and discus-

sion of Fig. 6.1b). In the extreme, this accretional growth leads to the formation of

hailstones. Associated with the large hydrometeor concentration resulting from

the strong upward air motions are feedbacks on the dynamics. The precipitation

particles can initiate downward acceleration by dragging air downward. Evapora-

tion and melting of the particles cool the air and thus also contribute to downdraft

formation and maintenance. Another characteristic of the rapidly moving convec-

tive updrafts and downdrafts in convective clouds is their turbulent nature, which

leads to entrainment of surrounding environmental air. Entrainment in turn modi-

fies the cloud dynamics and microphysics and is thus another important feedback

mechanism. Yet another important process associated with the convective drafts

is the development of in-cloud rotation, which in extreme cases is manifested in

the form of tornadoes. Rotation feeds back to the cloud dynamics by producing a

dynamical pressure field, which modifies the buoyancy-produced pressure field,

and by providing an additional mechanism (besides turbulence) for entrainment of

environmental air.

In this chapter, we will examine these basic dynamical characteristics, which

are fundamental to all convective clouds. Buoyancy and its related pressure per-

turbation field, turbulent entrainment, and the dynamics of rotation will be dis-

cussed in Sees. 7.1-7.4. In Sec. 7.5, we will describe how numerical models are

formulated to simulate convective clouds in such a way that these important

dynamical processes are taken into account, simultaneously connecting the cloud

dynamics with the microphysics, so that the microphysics are calculated in a

proper dynamical context and are able to interact with the dynamics. These topics

are applicable to all the forms of cumulus and cumulonimbus listed above. They

are introduced in this chapter at a basic level that will provide background for

general study of convective clouds. In subsequent chapters some of these topics

will be pursued further as we explore in more detail the dynamics of individual

cumulonimbus (Chapter 8) and complexes

thunderstorms (Chapter 9).

7.1 Buoyancy

Since all convective clouds owe their existence to the fact that air becomes buoy-

ant on a local scale (less than about 10km), we begin by briefly recalling the nature

of the buoyancy

B, which appears as a contribution to vertical acceleration in the

anelastic form of the equation of motion (2.47). In the absence of friction, the

(7.2)

7.2 Pressure Perturbation

223

vertical component of the momentum equation is

Dw 1 dp*

- =

----+B

(7.1)

where, as in Chapter 2, w is the vertical velocity,

the reference-state density,

and

p* the deviation of the pressure from its reference-state value. The buoyancy

B, according to (2.48), is proportional to the deviation of the density from the

reference state. According to (2.50), the buoyancy may be decomposed into con-

tributions from temperature, water vapor, pressure perturbations, and the weight

of hydro meteors suspended in or falling through the air. In convective clouds all

four terms in (2.50) are of the same order of magnitude. A temperature perturba-

tion of absolute value 1 K is equivalent to a perturbation of 0.005 in water-vapor

mixing ratio, 3 hPa in pressure, or 0.003 in hydrometeor mixing ratio.

7.2 Pressure Perturbation

can be anticipated intuitively that buoyancy cannot exist without a simulta-

neous disruption of the pressure field. If a parcel of air of finite width and depth is

less dense than the air in a surrounding horizontally uniform, otherwise undis-

turbed atmosphere, then at the height of the base of the parcel, the pressure is

lower in the parcel than in the environment. This horizontal gradient of pressure

accelerates environmental air toward the base of the buoyant parcel. This inward

acceleration, moreover, is consistent with the need to replace the buoyant air at

this level when it moves upward. A complete, internally consistent picture of

mass, pressure, and momentum fields required to exist in association with a region

of buoyant air is, of course, implied by the basic equations. We can obtain this

picture by combining the horizontal and vertical equations of motion with the

continuity equation. Iffriction and Coriolis forces are ignored, the anelastic equa-

tion of motion (2.47) can be written in Eulerian form as

dV 1 *

- =

--Vp

+Bk-v·Vv

If we take the three-dimensional divergence of this equation after first multiplying

it by

Po, we obtain

~(V'

v) = _V

p* +

~(p.

B)-

V·

(p,

v- Vv)

dt 0

0 0

(7.3)

Recalling from (2.54) that the three-dimensional mass divergence in the anelastic

system is zero, we see that the left-hand side of (7.3) is zero, and a diagnostic

equation for the pressure perturbation is obtained:

2p*

= F

+ F

(7.4)

224 7 Cumulus Dynamics

where

(7.5)

and

(7.6)

Thus, the Laplacian of the pressure perturbation field in an anelastic fluid must be

consistent with the vertical gradient of buoyancy

and the three-dimensional

divergence of the advection field

•

is called the buoyancy source and F

the

dynamic source. The pressure perturbation may be thought of as the sum of two

partial pressures

p; and

such that

* * *

P = PB + PD

(7.7)

V2p~

= F

(7.8)

V2p~

= F

(7.9)

In Chapter 8 we will see that sometimes the dynamic source, and hence

Pb,

becomes dominant, especially when strong eddies form within a tornadic thunder-

storm, or in a density current outflow from a thunderstorm. We will defer further

discussion of the dynamic source until Chapter 8. Here we will investigate the part

P* produced by the buoyancy source.

may be helpful in this regard to note

that (7.8) is analogous to Poisson's equation in electrostatics, where -

plays the

role of a charge density,

is like the electrostatic potential, and -

Vp;

is equiva-

lent to the electric field.

For

simple spatial arrangements of buoyancy, we can thus

use known mathematical solutions of Poisson's equations to find the vector field

_p;;IVp;.

We will call this field, which is analogous to an electric field produced

by a particular spatial arrangement of charge density, the

buoyancy pressure-

gradient acceleration (BPGA) field.

This solution is illustrated qualitatively in Fig. 7.1 for a uniformly buoyant

parcel of finite dimensions. The plus and minus signs in the figure indicate the sign

-F

along the top and bottom of the parcel. Where

-F

> 0, the BPGA field

(i.e.,

_p;;IVp;)

diverges according to (7.8), and where

-F

< 0 the BPGA field

converges. Everywhere except the top and bottom of the parcel,

The lines

of the BPGA field are shown as streamlines, like lines of electric field for finite

horizontal parallel plates of opposite charge density. Within the parcel, the lines of

the BPGA field are downward. There is a divergence of the BPGA field at the top

of the parcel and convergence at the bottom. Outside the parcel, lines

offorce

are

up above the parcel, downward in the regions to the sides of the parcel, and

upward

just

below the parcel. These lines indicate the directions of forces acting

to produce the compensating motions in the environment that are required to

satisfy mass continuity when the buoyant parcel moves upward.

The downward lines of force shown inside the parcel in Fig. 7.1 imply that the

Figure 7.1

7.2 Pressure Perturbation

225

Figure 7.2

Figure 7.1 Vector field of buoyancy pressure-gradient force for a uniformly buoyant parcel of

finite dimensions in the

x-z

plane. The plus and minus signs indicate the sign of the buoyancy forcing

function

-a(p,j3)/az

along the top and bottom of the parcel.

Figure 7.2 Vector field of buoyancy pressure-gradient force for a uniformly buoyant parcel of

infinite horizontal dimensions. The plus and minus signs indicate the sign of the buoyancy forcing

function - a(p,,B)/az along the top and bottom of the parcel.

upward acceleration

buoyancy is counteracted to some degree by a downward

BPGA. This counteraction must

occur

because some of the buoyancy of the

parcel has to be used to move environmental air out of the way in order to

preserve mass continuity while the parcel rises. The only way that downward

BPGA could be absent would be to have the parcel's width shrink to

zero-a

nonsensical case, but nonetheless illustrative of the fact that a given amount

buoyancy produces a larger upward acceleration the narrower the parcel. In

cumulus and cumulonimbus clouds, the distribution of

B is such that BPGA is

often the same

order

of magnitude as B. The BPGA can be especially important

near the tops of growing clouds, where rising towers are actively pushing environ-

mental air

out

of the way.

The maximum magnitude is achieved by the BPGA when it exactly balances

If we let

= 0, then

dP*

B =

---

= -BPGA (7.10)

which is the case of hydrostatic balance (Sec. 2.2.4). In the strict mathematical

sense, this case occurs at the limit where the horizontal dimension of a buoyant

element as in Fig. 7.1 becomes infinite in horizontal extent. This fact can be seen

by multiplying (7.10) by

Po, taking

a/az

of both sides of the equation, and rearrang-

ing to obtain

(7.11)

226 7 Cumulus Dynamics

Then (7.4), (7.5), and (7.11) imply that

(7.12)

where V

H is the horizontal gradient operator. Thus, if the horizontal gradient of p*

is flat in at least one place, there is no horizontal variation of p*. The counterpart

of Fig. 7.1 for the hydrostatic case is shown in Fig. 7.2, which shows the lines of

force for a uniformly buoyant parcel of infinite horizontal extent.

7.3 Entrainment

7.3.1 General Considerations

Another important property common to all forms of cumulus and cumulonimbus

clouds is that environmental air crosses the cloud boundaries and dilutes the in-

cloud air. The net buoyancy and other properties of the cloudy air are thus

moderated, and the cloud is made less vigorous. In evaluating the average proper-

ties of the in-cloud air, the rate at which air is exchanged with the environment

must be taken into account.

Air may be drawn laterally into cumuliform clouds to satisfy mass continuity if

the mean mass flux in the cloud is increasing with respect to height. In addition,

mixing across the cloud boundaries occurs as a result of the highly turbulent air

motions characterizing all forms of cumulus and cumulonimbus clouds. Within

convective clouds both strong shear and strong buoyancy exist. Hence, both the

conversion from shear

<{6

and the buoyancy generation ~ in (2.86) are important

sources of turbulent kinetic energy. The intensity of the turbulence in the cloud is

much greater than in the surrounding environment. Some of the internal cloud

motions take the form of organized overturning and rotation on the scale of the

cloud itself, while some of the turbulence is of a smaller scale and more random.

Mixing occurs across all the edges of the cloud, as a result of both the random and

the organized motions. As a result of these motions and the general necessity to

satisfy mass continuity, the cloud becomes diluted by a certain proportion of

environmental air. The incorporation of environmental air into the cloud is called

entrainment. In Chapter 5, we saw how entrainment across the tops and bottoms

of mixed-layer stratiform clouds led to their dilution. In the convective clouds

considered in the present chapter, the internal motions producing the entrainment

are more vigorous, and mixing occurs across the sides as well as the tops and

bottoms of cloud elements.

In this section, we investigate the mechanism of entrainment in convective

clouds, and we shall proceed in an historical vein. First, we examine some early

ideas, which present a simple, sometimes useful, but basically flawed approxima-

tion to the process of entrainment. We call this traditional view

continuous,

homogeneous entrainment,

since it treats the process as continuous in time and

uniform in space. We will then examine the modern view, which we will call

7.3 Entrainment 227

discontinuous, inhomogeneous entrainment, in which entrainment is considered

to be a discrete process in time and space.

7.3.2 Continuous, Homogeneous Entrainment

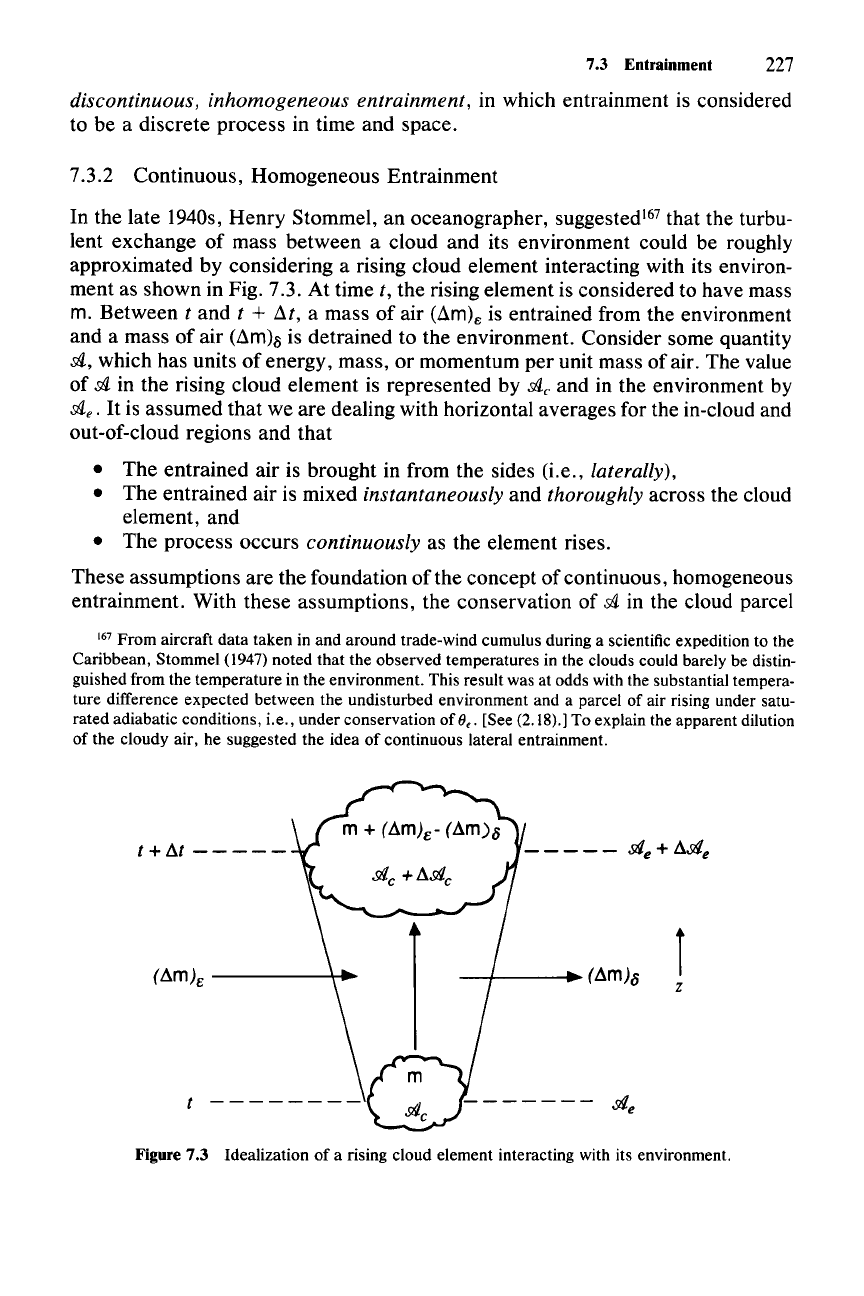
In the late 1940s,

Henry

Stornmel, an oceanographer, suggested's? that the turbu-

lent exchange

mass between a cloud and its environment could be roughly

approximated by considering a rising cloud element interacting with its environ-

ment as shown in Fig. 7.3. At time

t, the rising element is considered to have mass

m. Between t

and

t +

at,

a mass of air (am)e is entrained from the environment

and a mass of air

(am),') is detrained to the environment. Consider some quantity

sl; which has units

energy, mass, or momentum

per

unit mass of air. The value

d in the rising cloud element is represented by

and in the environment by

de'

is assumed

that

we are dealing with horizontal averages for the in-cloud and

out-of-cloud regions and that

•

The

entrained air is brought in from the sides (i.e., laterally),

•

The

entrained air is mixed instantaneously and thoroughly across the cloud

element,

and

•

The

process

occurs

continuously as the element rises.

These assumptions are the foundation of the concept of continuous, homogeneous

entrainment. With these assumptions, the conservation of

d in the cloud parcel

167 From aircraft data taken in and around trade-wind cumulus during a scientific expedition to the

Caribbean, Stommel (1947) noted that the observed temperatures in the clouds could barely be distin-

guished from the temperature in the environment. This result was at odds with the substantial tempera-

ture difference expected between the undisturbed environment and a parcel of air rising under satu-

rated adiabatic conditions, i.e., under conservation of

0,. [See (2.18).] To explain the apparent dilution

of the cloudy air, he suggested the idea of continuous lateral entrainment.

t+Llt

-----

--------

-+---.

(Llm)o

Figure 7.3 Idealization of a rising cloud element interacting with its environment.

(7.13)

228

7 Cumulus Dynamics

can be written as

[m+(l1m)e-

(I1m)s](31

e+I131

)

m31

e+31

(I1m)e

-31

(I1m)s

+ (l131

) ml1t

M s

where

(l131

ell1th

is the rate of change of

that would be present even if the

parcel was not exchanging mass with the environment. Rearrangement of terms in

(7.13) and taking the limit as

I1t

0 leads to

D31

= (D31

~(Dm)

(31

) (7.14)

Dt Dt m Dt e c

S e

where the notation DIDt, as usual [see (2.2)], indicates a derivative following a

parcel of fluid. The detrainment terms in (7.13) cancel and do not appear in (7.14)

since

detrainment

mass

in no way affects the mass-averaged values

vari-

ables in the cloud.

is only entrainment that affects the in-cloud averages, since it

dilutes the parcel with environmental fluid.

As we will see in Sec. 7.3.2, modern observations show that the entrainment

process in cumulus clouds is

not

continuous, instantaneous, thorough, or entirely

lateral; thus, an accurate representation of the process must take these facts into

account. Nonetheless, the above continuous view has some value in providing a

simple and tractable first approximation to cumulus dynamics.

The role of entrainment in the First Law of Thermodynamics may be seen by

applying (7.14) to the

moist static energy

,f"

cpT + Lq; + gz (7.15)

In the absence of entrainment and diabatic processes other than release of latent

heat in condensation or evaporation (ignoring ice-phase processes), the First Law

is given by (2.12).

the pressure change following a parcel is to a first approxima-

tion hydrostatic, then taking

D(7.15)/Dt, with substitution from (2.12) and (2.38),

yields

(

,f"

C) = 0

Dt s

In this case, (7.14) becomes

D,f"c

=~(Dm)

(,f" -,f,,)

Dt m Dt e e c

(7.16)

(7.17)

when s is substituted for

31.

Using the definition (7.15), we may rewrite (7.17) as

(7.18)