Hjorth-Jensen M. Computational Physics
Подождите немного. Документ загружается.


10.3. MICROSCOPIC DERIVATION OF THE DIFFUSION EQUATION 179
ofstream o f i l e ( ) ;
ofstream p rob f i l e ( ) ;
for ( int i = 1 ; i <= number_walks ; i ++){
double xaverage = walk_cumulative [ i ] / ( ( double ) m ax_trials ) ;
double x2average = walk2_cumulative [ i ] / ( ( double ) max_trials ) ;
double variance = x2average xaverage xaverage ;
o f i l e < < s e t i o s f l a g s ( ios : : showpoint | ios : : uppercase ) ;
o f i l e < < setw (6) < < i ;
o f i l e < < setw (15) < < se t p r e c i s ion (8) < < xaverage ;
o f i l e < < setw (15) < < se t p r e c i s ion (8) < < variance < < endl ;
}
o f i l e . close ( ) ;
/ / find norm of p rob a bil i ty
double norm = 0 . ;
for ( int i = number_walks ; i <= number_walks ; i ++){
norm += ( double ) p r o b a bili t y [ i +number_walks ] ;
}
/ / write p r o ba b i li t y
for ( int i = number_walks ; i <= number_walks ; i ++){
double histogram = p r o b abi l i t y [ i+number_walks ] / norm ;
pro b f ile < < s e t i o s f l a g s ( ios : : showpoint | ios : : uppercase ) ;
pro b f ile < < setw (6) < < i ;
pro b f ile < < setw (15) < < setp r e c i s i o n (8) < < histogram < < endl ;
}
pro b f ile . close ( ) ;
} / / end of fun ctio n output
The sampling part is still done in the same function, but contains now the setup of a histogram
containing the number of times the walker visited a given position .
void mc_sampling ( int max_trials , int number_walks ,
double move_probability , int walk_cumulative ,
int walk2_cumulative , int p r o b a bili t y )
{
long idum ;
idum = 1; / / i n i t i a l i s e random number generator
for ( int t r i a l = 1; t r i a l <= max_trials ; t r i a l ++){
int p osi tion = 0;
for ( int walks = 1 ; walks <= number_walks ; walks ++){
i f ( ran0(&idum ) <= move_probability ) {
pos iti on + = 1;
}
else {
pos iti on = 1;
}
walk_cumulative [ walks ] += p osi tio n ;
180 CHAPTER 10. RANDOM WALKS AND THE METROPOLIS ALGORITHM
walk2_cumulative [ walks ] += p ositi on po s it i on ;
prob abi l i t y [ po sitio n +number_walks ] + = 1;
} / / end of loop over walks
} / / end of loop over t r i a l s
} / / end mc_sampling function
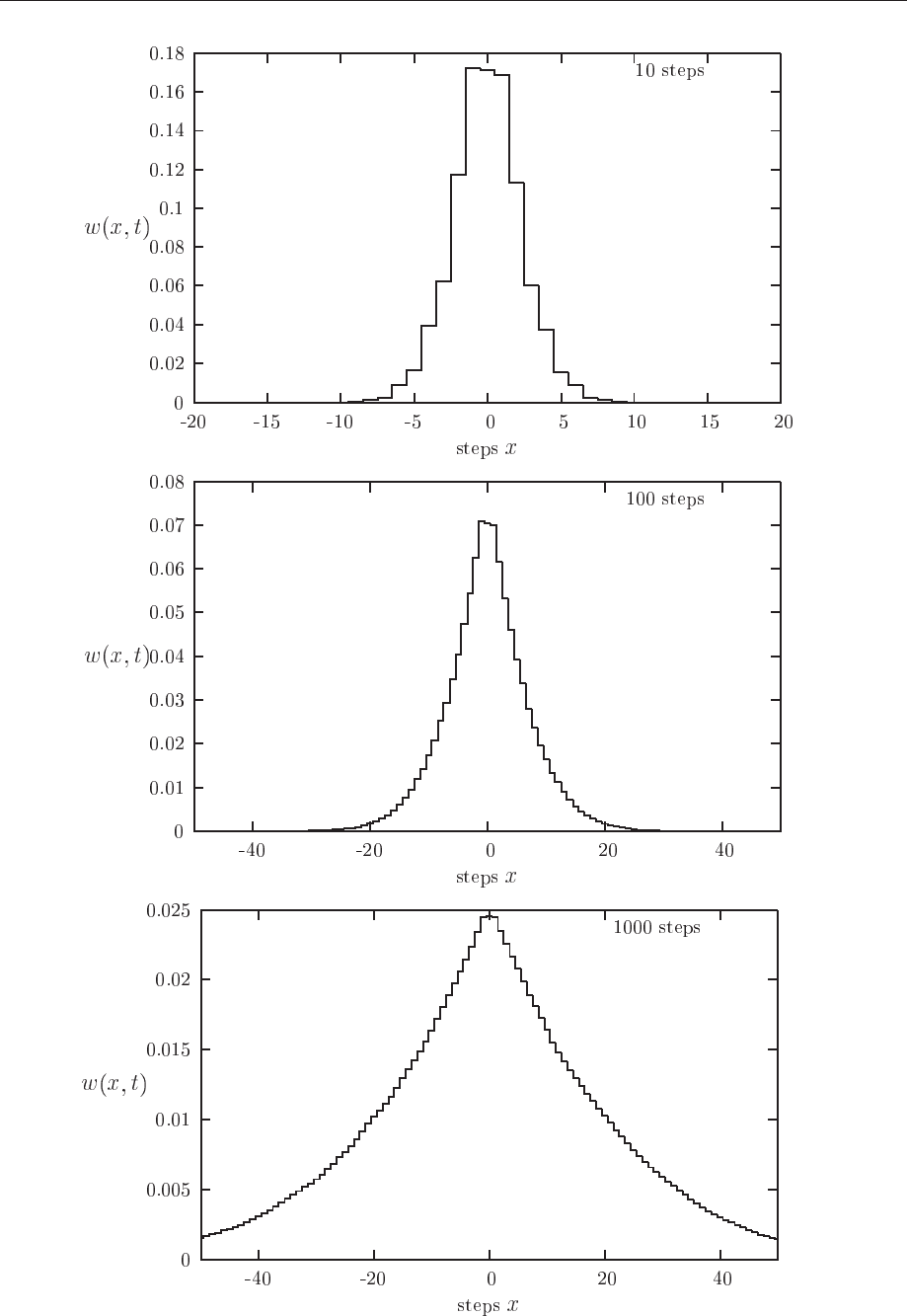
Fig. 10.5 shows the resulting probability distribution after steps We see from Fig. 10.5 that the
probability distribution function resembles a normal distribution.
Exercise 10.2
Use the above program and try to fit the computed probability distribution with a
normal distribution using your calculated values of and .
10.4 The Metropolis algorithm and detailed balance
An important condition we require that our Markov chain should satisfy is that of detailed bal-
ance. In statistical physics this condition ensures that it is e.g., the Boltzmann distribution which
is generated when equilibrium is reached. The definition for being in equilibrium is that the rates
at which a system makes a transition to or from a given state have to be equal, that is
(10.66)
Another way of stating that a Markow process has reached equilibrium is
(10.67)
However, the condition that the rates should equal each other is in general not sufficient to guar-
antee that we, after many simulations, generate the correct distribution. We therefore introduce
an additional condition, namely that of detailed balance
(10.68)
Satisfies the detailed balance condition. At equilibrium detailed balance gives thus
(10.69)
We introduce the Boltzmann distribution
(10.70)
which states that probability of finding the system in a state
with energy at an inverse
temperature is . The denominator is a normalization constant
10.4. THE METROPOLIS ALGORITHM AND DETAILED BALANCE 181
Figure 10.5: Probability distribution for one walker after 10, 100 and 1000 steps.
182 CHAPTER 10. RANDOM WALKS AND THE METROPOLIS ALGORITHM
which ensures that the sum of all probabilities is normalized to one. It is defined as the sum of
probabilities over all microstates
of the system
(10.71)
From the partition function we can in principle generate all interesting quantities for a given
system in equilibrium with its surroundings at a temperature . This is demonstrated in the next
chapter.
With the probability distribution given by the Boltzmann distribution we are now in the posi-
tion where we can generate expectation values for a given variable
through the definition
(10.72)
In general, most systems have an infinity of microstates making thereby the computation of
practically impossible and a brute force Monte Carlo calculation over a given number of ran-
domly selected microstates may therefore not yield those microstates which are important at
equilibrium. To select the most important contributions we need to use the condition for detailed
balance. Since this is just given by the ratios of probabilities, we never need to evaluate the
partition function
. For the Boltzmann distribution, detailed balance results in
(10.73)
Let us now specialize to a system whose energy is defined by the orientation of single spins.
Consider the state
, with given energy represented by the following spins
We are interested in the transition with one single spinflip to a new state with energy
This change from one microstate (or spin configuration) to another microstate is the con-
figuration space analogue to a random walk on a lattice. Instead of jumping from one place to
another in space, we ’jump’ from one microstate to another.
However, the selection of states has to generate a final distribution which is the Boltzmann
distribution. This is again the same we saw for a random walker, for the discrete case we had al-
ways a binomial distribution, whereas for the continuous case we had a normal distribution. The
way we sample configurations should result in, when equilibrium is established, in the Boltz-
mann distribution. Else, our algorithm for selecting microstates has to be wrong.
Since we do not know the analytic form of the transition rate, we are free to model it as
(10.74)
10.4. THE METROPOLIS ALGORITHM AND DETAILED BALANCE 183
where is a selection probability while is the probability for accepting a move. It is also called
the acceptance ratio. The selection probability should be same for all possible spin orientations,
namely
(10.75)
With detailed balance this gives
(10.76)
but since the selection ratio is the same for both transitions, we have
(10.77)
In general, we are looking for those spin orientations which correspond to the average energy at
equilibrium.
We are in this case interested in a new state whose energy is lower than , viz.,
. A simple test would then be to accept only those microstates which lower the
energy. Suppose we have ten microstates with energy . Our
desired energy is . At a given temperature we start our simulation by randomly choosing
state
. Flipping spins we may then find a path from . This
would however lead to biased statistical averages since it would violate the ergodic hypothesis
which states that it should be possible for any Markov process to reach every possible state of
the system from any starting point if the simulations is carried out for a long enough time.
Any state in a Boltzmann distribution has a probability different from zero and if such a state
cannot be reached from a given starting point, then the system is not ergodic. This means that
another possible path to
could be and so forth. Even
though such a path could have a negligible probability it is still a possibility, and if we simulate
long enough it should be included in our computation of an expectation value.
Thus, we require that our algorithm should satisfy the principle of detailed balance and be
ergodic. One possible way is the Metropolis algorithm, which reads
(10.78)
This algorithm satisfies the condition for detailed balance and ergodicity. It is implemented as
follows:
Establish an initial energy
Do a random change of this initial state by e.g., flipping an individual spin. This new state
has energy . Compute then
If accept the new configuration.

184 CHAPTER 10. RANDOM WALKS AND THE METROPOLIS ALGORITHM
If , compute .
Compare with a random number . If accept, else keep the old configuration.
Compute the terms in the sums .
Repeat the above steps in order to have a large enough number of microstates
For a given number of MC cycles, compute then expectation values.
The application of this algorithm will be discussed in detail in the next two chapters.
10.5 Physics project: simulation of the Boltzmann distribu-
tion
In this project the aim is to show that the Metropolis algorithm generates the Boltzmann distri-
bution
(10.79)
with
being the inverse temperature, is the energy of the system and is the partition
function. The only functions you will need are those to generate random numbers.
We are going to study one single particle in equilibrium with its surroundings, the latter
modeled via a large heat bath with temperature
.
The model used to describe this particle is that of an ideal gas in one dimension and with
velocity
or . We are interested in finding , which expresses the probability for
finding the system with a given velocity
. The energy for this one-dimensional
system is
(10.80)
with mass . In order to simulate the Boltzmann distribution, your program should contain
the following ingredients:
Reads in the temperature , the number of Monte Carlo cycles, and the initial velocity.
You should also read in the change in velocity used in every Monte Carlo step. Let the
temperature have dimension energy.
Thereafter you choose a maximum velocity given by e.g., . Then you con-
struct a velocity interval defined by
and divided it in small intervals through ,
with . For each of these intervals your task is to find out how many times
a given velocity during the Monte Carlo sampling appears in each specific interval.
The number of times a given velocity appears in a specific interval is used to construct a
histogram representing . To achieve this you should construct a vector which
contains the number of times a given velocity appears in the subinterval .
10.5. PHYSICS PROJECT: SIMULATION OF THE BOLTZMANN DISTRIBUTION185
In order to find the number of velocities appearing in each interval we will employ the
Metropolis algorithm. A pseudocode for this is
for ( montecarlo_cycles =1; Max_cycles ; montecarlo_cycles ++) {
. . .
/ / change speed as fu nc tion of d el ta v
v_change = ( 2 ran1 (&idum ) 1 ) delta_v ;
v_new = v_old+v_change ;
/ / energy change
delta_E = 0 .5 ( v_new v_new v_old v_old ) ;
. . . . . .
/ / Metropolis algorithm begins here
i f ( ran1 (&idum ) <= exp( beta delta_E ) ) {
acc ept_step = accept _step + 1 ;
v_old = v_new ;
. . . . .
}
/ / t h ereaf t er we must f i l l in P[N] as a f unct ion of
/ / the new speed
P [ ? ] = . . .
/ / upgrade mean v eloc it y , energy and variance
. . .
}
a) Make your own algorithm which sets up the histogram , find mean velocity, energy,
energy variance and the number of accepted steps for a given temperature. Study the
change of the number of accepted moves as a function of
. Compare the final energy
with the analytic result for one dimension. Use and set the intial velocity
to zero, i.e.,
. Try different values of . A possible start value is . Check the
final result for the energy as a function of the number of Monte Carlo cycles.
b) Make thereafter a plot of
as function of and see if you get a straight line.
Comment the result.

Chapter 11
Monte Carlo methods in statistical physics
The aim of this chapter is to present examples from the physical sciences where Monte Carlo
methods are widely applied. Here we focus on examples from statistical physics. and discuss
one of the most studied systems, the Ising model for the interaction among classical spins. This
model exhibits both first and second order phase transitionsand is perhaps one of the most studied
cases in statistical physics and discussions of simulations of phase transitions.
11.1 Phase transitions in magnetic systems
11.1.1 Theoretical background
The model we will employ in our studies of phase transitions at finite temperature for magnetic
systems is the so-called Ising model. In its simplest form the energy is expressed as
(11.1)
with
, is the total number of spins, is a coupling constant expressing the strength
of the interaction between neighboring spins and is an external magnetic field interacting with
the magnetic moment set up by the spins. The symbol
indicates that we sum over nearest
neighbors only. Notice that for it is energetically favorable for neighboring spins to be
aligned. This feature leads to, at low enough temperatures, to a cooperative phenomenon called
spontaneous magnetization. That is, through interactions between nearest neighbors, a given
magnetic moment can influence the alignment of spins that are separated from the given spin
by a macroscopic distance. These long range correlations between spins are associated with a
long-range order in which the lattice has a net magnetization in the absence of a magnetic field.
In our further studies of the Ising model, we will limit the attention to cases with
only.
In order to calculate expectation values such as the mean energy
or magnetization
in statistical physics at a given temperature, we need a probability distribution
(11.2)
187
188 CHAPTER 11. MONTE CARLO METHODS IN STATISTICAL PHYSICS
with being the inverse temperature, the Boltzmann constant, is the energy of a
state
while is the partition function for the canonical ensemble defined as
(11.3)
where the sum extends over all states
. expresses the probability of finding the system in a
given configuration .
The energy for a specific configuration is given by
(11.4)
To better understand what is meant with a configuration, consider first the case of the one-
dimensional Ising model with
. In general, a given configuration of spins in one
dimension may look like
In order to illustrate these features let us further specialize to just two spins.
With two spins, since each spin takes two values only, it means that in total we have
possible arrangements of the two spins. These four possibilities are
What is the energy of each of these configurations?
For small systems, the way we treat the ends matters. Two cases are often used
1. In the first case we employ what is called free ends. For the one-dimensional case, the
energy is then written as a sum over a single index
(11.5)
If we label the first spin as
and the second as we obtain the following expression for
the energy
(11.6)
The calculation of the energy for the one-dimensional lattice with free ends for one specific
spin-configuration can easily be implemented in the following lines
for ( j =1; j < N; j ++) {
energy += spin [ j ] spin [ j +1];
}
