Hjorth-Jensen M. Computational Physics
Подождите немного. Документ загружается.

Chapter 17
Modelling phase transitions
17.1 Methods to classify phase transition
17.1.1 The histogram method
17.1.2 Multi-histogram method
17.2 Renormalization group approach
319
Chapter 18
Hydrodynamic models
321
Chapter 19
Diffusion Monte Carlo methods
We discuss implementations and the underlying theory for diffusion Monte Carlo methods.
19.1 Diffusion Monte Carlo
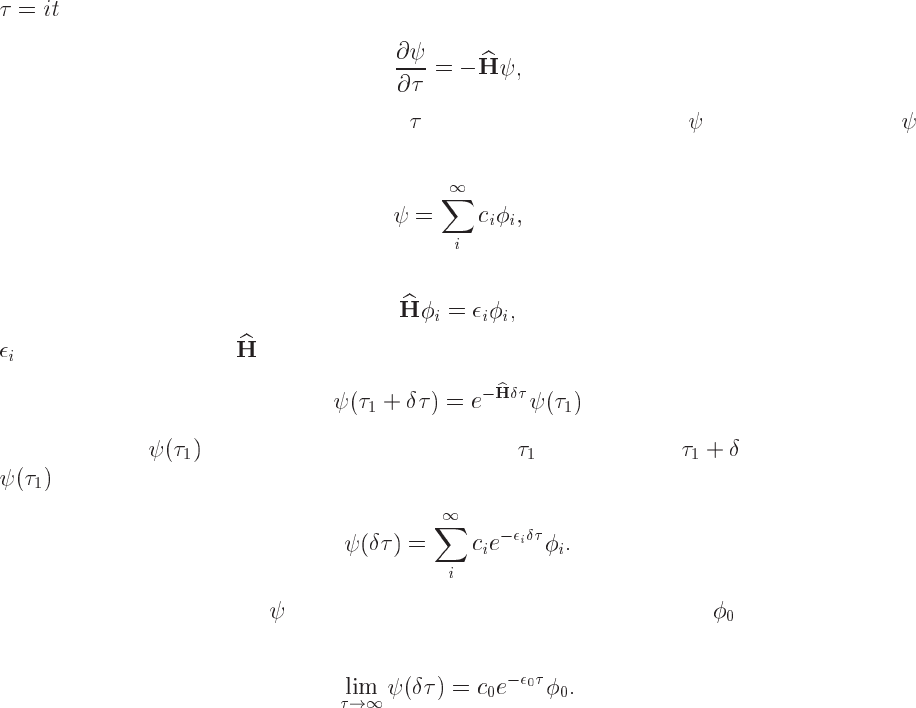
The DMC method is based on rewriting the Schrödinger equation in imaginary time, by defining
. The imaginary time Schrödinger equation is then
(19.1)
where we have omitted the dependence on
and the spatial variables in . The wave function
is again expanded in eigenstates of the Hamiltonian
(19.2)
where
(19.3)
being an eigenstate of . A formal solution of the imaginary time Schrödinger equation is
(19.4)
where the state
evolves from an imaginary time to a later time . If the initial state
is expanded in energy ordered eigenstates, following Eq. (19.2), then we obtain
(19.5)
Hence any initial state, , that is not orthogonal to the ground state will evolve to the
ground state in the long time limit, that is
(19.6)
323

324 CHAPTER 19. DIFFUSION MONTE CARLO METHODS
This derivation shares many formal similarities with that given for the variational principle dis-
cussed in the previous sections. However in the DMC method the imaginary time evolution
results in excited states decaying exponentially fast, whereas in the VMC method any excited
state contributions remain and contribute to the VMC energy.
The DMC method is a realisation of the above derivation in position space. Including the
spatial variables as well, the above equation reads
(19.7)
By introducing a constant offset to the energy,
, the long-time limit of Eq. (19.7)
can be kept finite. If the Hamiltonian is separated into the kinetic energy and potential terms, the
imaginary time Schrödinger equation, takes on a form similar to a diffusion equation, namely
(19.8)
This equation is a diffusion equation where the wave function
may be interpreted as the density
of diffusingparticles (or “walkers”), and the term isa rate term describing a potential-
dependent increase or decrease in the particle density. The above equation may be transformed
into a form suitable for Monte Carlo methods, but this leads to a very inefficient algorithm.
The potential
is unbounded in coulombic systems and hence the rate term
can diverge. Large fluctuations in the particle density then result and give impractically large
statistical errors.
These fluctuations may be substantially reduced by the incorporation of importance sampling
in the algorithm. Importance sampling is essential for DMC methods, if the simulation is to
be efficient. A trial or guiding wave function
, which closely approximates the ground
state wave function is introduced. This is where typically the VMC result would enter, see also
discussion below A new distribution is defined as
(19.9)
which is also a solution of the Schrödinger equation when
is a solution. Eq. (19.8)
consequently modified to
(19.10)
In this equation we have introduced the so-called force-term
, given by
(19.11)
and is commonly referred to as the “quantum force”. The local energy
is defined as previously
(19.12)

19.2. OTHER QUANTUM MONTE CARLO TECHNIQUES AND SYSTEMS 325
and is computed, as in the VMC method, with respect to the trial wave function.
We can give the following interpretation to Eq. (19.10). The right hand side of the impor-
tance sampled DMC equation consists, from left to right, of diffusion, drift and rate terms. The
problematic potential dependent rate term of the non-importance sampled method is replaced by
a term dependent on the difference between the local energy of the guiding wave function and the
trial energy. The trial energy is initially chosen to be the VMC energy of the trial wave function,
and is updated as the simulation progresses. Use of an optimised trial function minimises the
difference between the local and trial energies, and hence minimises fluctuations in the distribu-
tion
. A wave function optimised using VMC is ideal for this purpose, and in practice VMC
provides the best method for obtaining wave functions that accurately approximate ground state
wave functions locally. The trial wave function may be also constructed to minimise the number
of divergences in , unlike the non-importance sampled method where divergences in the coulomb
interactions are always present.
To be of use however, the importance sampled DMC method of Eq. (19.10) must be trans-
formed into a form suitable for Monte Carlo integration. The transformation is more complex
than for VMC, which simply required the insertion of the factor
into the conventional formulas for quantum mechanical expectation values.
A Green’s function
that is a solution of Eq. (19.10) is desired, i.e., a spatial
representation of the imaginary time propagator,
. One can show that the Green’s
function of the diffusion equation, by factorising the propagator into branching and diffusion
parts, can be written as
(19.13)
19.2 Other Quantum Monte Carlo techniques and systems
In our discussion, the emphasis has been on variational methods, since they are rather intuitive
and one can simulate physical systems with rather simple trial wave functions. We have also not
dealt with problems arising in many-fermion systems, where both the sign of the wave function
in the diffusion Monte Carlo is crucial and the evaluation of the Slater determinant is computa-
tionally involved. Furthermore, techniques to improve the variance have also not been discussed.
We defer these topics, together with a discussion of other Monte Carlo methods such as Green’s
function Monte Carlo, path integral Monte Carlo and Lattice methods to a more advanced course
on computational Physics.
Chapter 20
Finite element method
327
