Hjorth-Jensen M. Computational Physics

Подождите немного. Документ загружается.

14.7. PHYSICS PROJECT: THE PENDULUM 279

out [1 ] = ( phi ) ’ ’

el se

out [1]= sin ( in [ 0 ]) +A_roof cos ( omega_roof t ) ; / / out [ 1] = ( phi ) ’ ’

}

void pendelum : : i n i t i a l i s e ()

{

double m, l , omega ,A, vi scosi ty , phi_0 , v_0 , t_end ;

cout << ;

cout <<

;

cout << ;

cin >>m;

cout << ;

cin >> l ;

cout << ;

cin >>omega ;

cout << ;

cin >>A;

cout << ;

cin >> v i sco s i t y ;

cout << ;

cin >>y [ 0 ] ;

cout << ;

cin >>y [ 1 ] ;

cout << ;

cin >>n ;

cout << ;

cin >>t_end ;

t_end = acos ( 1.) ;

g =9.81;

/ / We need the fol low ing values :

omega_0= sqr t ( g / ( ( double ) l ) ) ; / / omega of the pendulum

i f ( vi s c o s i ty ) Q= m g / ( ( double ) omega_0 visc o s i t y ) ;

el se Q=0; / / ca lcu la t in g Q

A_roof=A/ ( ( double )m g) ;

omega_roof=omega / ( ( double ) omega_0 ) ;

del t a_t _ ro o f =omega_0 t_end / ( ( double )n) ; / / de lta_ t without

dimension

delt a _ t =t_end / ( ( double ) n) ;

}

280 CHAPTER 14. DIFFERENTIAL EQUATIONS

void pendelum : : eu ler ( )

{ / / using simple euler method

int i ;

double yout [2] , y_h [ 2 ] ;

double t_h ;

y_h [0]= y [ 0 ] ;

y_h [1]= y [ 1 ] ;

t_h =0;

ofstream fout ( ) ;

fout . s e tf ( ios : : s c i e n t i f i c ) ;

fout . preci si o n (20) ;

for ( i =1; i <=n ; i ++){

deri v a t i v es ( t_h , y_h , yout ) ;

yout [1]= y_h [1]+ yout [1] del ta_ t _r o of ;

yout [0]= y_h [0]+ yout [0] del ta_ t _r o of ;

/ / Calculation with dimensionless values

fout << i delta _t << <<yout [0] << <<yout [1] < < ;

t_h+= d el t a_t _ro o f ;

y_h [1]= yout [ 1 ] ;

y_h [0]= yout [ 0 ] ;

}

fout . close ;

}

void pendelum : : euler_cromer ()

{

int i ;

double t_h ;

double yout [2] , y_h [ 2 ] ;

t_h =0;

y_h [0]= y [ 0 ] ; / / phi

y_h [1]= y [ 1 ] ; / / v

ofstream fout ( ) ;

fout . s e tf ( ios : : s c i e n t i f i c ) ;

fout . preci si o n (20) ;

for ( i =1; i <=n ; i ++){

deri v a t i v es ( t_h , y_h , yout ) ;

yout [1]= y_h [1]+ yout [1] del ta_ t _r o of ;

yout [0]= y_h [0]+ yout [1] del ta_ t _r o of ;

/ / The new calcula ted value of v i s used for c al c ul a ti ng phi

fout << i delta _t << <<yout [0] << <<yout [1] < < ;

t_h+= d el t a_t _ro o f ;

y_h [0]= yout [ 0 ] ;

14.7. PHYSICS PROJECT: THE PENDULUM 281

y_h [1]= yout [ 1 ] ;

}

fout . close ;

}

void pendelum : : midpoint ( )

{

int i ;

double t_h ;

double yout [2] , y_h [ 2 ] ;

t_h =0;

y_h [0]= y [ 0 ] ; / / phi

y_h [1]= y [ 1 ] ; / / v

ofstream fout ( ) ;

fout . s e tf ( ios : : s c i e n t i f i c ) ;

fout . preci si o n (20) ;

for ( i =1; i <=n ; i ++){

deri v a t i v es ( t_h , y_h , yout ) ;

yout [1]= y_h [1]+ yout [1] del ta_ t _r o of ;

yout [0]= y_h [0]+0.5 ( yout [1]+ y_h [ 1 ]) d el t a_t _ro o f ;

fout << i delta _t << <<yout [0] << <<yout [1] < < ;

t_h+= d el t a_t _ro o f ;

y_h [0]= yout [ 0 ] ;

y_h [1]= yout [ 1 ] ;

}

fout . close ;

}

void pendelum : : eu ler_ ri ch ar ds on ()

{

int i ;

double t_h , t_m ;

double yout [2] , y_h [2 ] , y_m [ 2 ] ;

t_h =0;

y_h [0]= y [ 0 ] ; / / phi

y_h [1]= y [ 1 ] ; / / v

ofstream fout ( ) ;

fout . s e tf ( ios : : s c i e n t i f i c ) ;

fout . preci si o n (20) ;

for ( i =1; i <=n ; i ++){

deri v a t i v es ( t_h , y_h , yout ) ;

y_m[1]= y_h [1]+0.5 yout [1] del t a_ t _ro of ;

282 CHAPTER 14. DIFFERENTIAL EQUATIONS

y_m[0]= y_h [0]+0.5 y_h [1] del ta_t _r o of ;

t_m=t_h +0.5 d e lt a _t_r oo f ;

deri v a t i v es ( t_m , y_m , yout ) ;

yout [1]= y_h [1]+ yout [1] del ta_ t _r o of ;

yout [0]= y_h [0]+ y_m[1] del ta_ t _ro of ;

fout << i delta _t << <<yout [0] << <<yout [1] < < ;

t_h+= d el t a_t _ro o f ;

y_h [0]= yout [ 0 ] ;

y_h [1]= yout [ 1 ] ;

}

fout . close ;

}

void pendelum : : hal f_ s te p ( )

{

/ We are using the hal f_s t ep_a lgor i th .

The algorithm i s not self st ar ti ng , so we ca lc u la te

v_1 / 2 by using the Euler algorithm . /

int i ;

double t_h ;

double yout [2] , y_h [ 2 ] ;

t_h =0;

y_h [0]= y [ 0 ] ; / / phi

y_h [1]= y [ 1 ] ; / / v

ofstream fout ( ) ;

fout . s e tf ( ios : : s c i e n t i f i c ) ;

fout . preci si o n (20) ;

/ At f i r s t we have to cal cu l at e v_1 /2

For t h i s we use Euler ’ s method :

v_ ‘ 1/2 = v_0 + 1/2 a_0 de lta _t _ro of

For c a lc ula ti n g a_0 we have to s t a r t der i vat i v e s

deri v a t i v es ( t_h , y_h , yout ) ;

yout [1]= y_h [1]+0.5 yout [1] d e lta _t_ r oo f ;

yout [0]= y_h [0]+ yout [1] de l ta_ t_r o of ;

fout << delta_t << <<yout [0] << <<yout [1] << ;

y_h [0]= yout [ 0 ] ;

y_h [1]= yout [ 1 ] ;

for ( i =2; i <=n ; i ++){

deri v a t i v es ( t_h , y_h , yout ) ;

yout [1]= y_h [1]+ yout [1] del ta_ t _r o of ;

yout [0]= y_h [0]+ yout [1] del ta_ t _r o of ;

fout << i delta _t << <<yout [0] << <<yout [1] < < ;

14.7. PHYSICS PROJECT: THE PENDULUM 283

t_h+= d el t a_t _ro o f ;

y_h [0]= yout [ 0 ] ;

y_h [1]= yout [ 1 ] ;

}

fout . close ;

}

void pendelum : : rk2 ( )

{

/ We are using the second order Runge Kutta algorithm

We have to ca lcu late the parameters k1 and k2 for v and phi ,

so we use to arrays k1 [ 2] and k2 [ 2] for t h i s

k1 [ 0 ] , k2 [ 0] are the parameters for phi ,

k1 [ 1 ] , k2 [ 1] are the parameters for v

int i ;

double t_h ;

double yout [2] , y_h [2 ] , k1 [2] , k2 [2] , y_k [ 2 ] ;

t_h =0;

y_h [0]= y [ 0 ] ; / / phi

y_h [1]= y [ 1 ] ; / / v

ofstream fout ( ) ;

fout . s e tf ( ios : : s c i e n t i f i c ) ;

fout . preci si o n (20) ;

for ( i =1; i <=n ; i ++){

/ Calculation of k1 /

deri v a t i v es ( t_h , y_h , yout ) ;

k1 [1]= yout [1] del ta_ t _r oof ;

k1 [0]= yout [0] del ta_ t _r oof ;

y_k [0]= y_h [0]+ k1 [ 0 ] 0 . 5 ;

y_k [1]= y_h [1]+ k2 [ 1 ] 0 . 5 ;

/ Calculation of k2 /

deri v a t i v es ( t_h+ d e lta _t_ r oo f 0.5 , y_k , yout ) ;

k2 [1]= yout [1] del ta_ t _r oof ;

k2 [0]= yout [0] del ta_ t _r oof ;

yout [1]= y_h [1]+ k2 [ 1] ;

yout [0]= y_h [0]+ k2 [ 0] ;

fout << i delta _t << <<yout [0] << <<yout [1] < < ;

t_h+= d el t a_t _ro o f ;

y_h [0]= yout [ 0 ] ;

y_h [1]= yout [ 1 ] ;

}

fout . close ;

284 CHAPTER 14. DIFFERENTIAL EQUATIONS

}

void pendelum : : rk4_step ( double t , double yin , double yout , double

delt a _ t )

{

The fun ction c a lcu lat es one step of fourth order runge kutta

method

We w ill need i t for the normal fourth order Runge Kutta method and

for RK method with adaptive s t e p s i ze cont rol

The fun ction c a lcu lat es the value of y ( t + delt a_t ) using fourth

order RK method

Input : time t and the s tepsi z e delta_t , yin ( values of phi and v

at time t )

Output : yout ( values of phi and v at time t+delta_t )

double k1 [2] , k2 [2] , k3 [2] , k4 [2] , y_k [ 2 ] ;

/ / Calculation of k1

deri v a t i v es ( t , yin , yout ) ;

k1 [1]= yout [1] d elta _ t ;

k1 [0]= yout [0] d elta _ t ;

y_k [0]= yin [0]+ k1 [ 0] 0 . 5;

y_k [1]= yin [1]+ k1 [ 1] 0 . 5;

/ Calculation of k2 /

deri v a t i v es ( t+ d e lta_ t 0.5 , y_k , yout ) ;

k2 [1]= yout [1] d elta _ t ;

k2 [0]= yout [0] d elta _ t ;

y_k [0]= yin [0]+ k2 [ 0] 0 . 5;

y_k [1]= yin [1]+ k2 [ 1] 0 . 5;

/ Calculation of k3 /

deri v a t i v es ( t+ d e lta_ t 0.5 , y_k , yout ) ;

k3 [1]= yout [1] d elta _ t ;

k3 [0]= yout [0] d elta _ t ;

y_k [0]= yin [0]+ k3 [ 0 ] ;

y_k [1]= yin [1]+ k3 [ 1 ] ;

/ Calculation of k4 /

deri v a t i v es ( t+delta_t , y_k , yout ) ;

k4 [1]= yout [1] d elta _ t ;

k4 [0]= yout [0] d elta _ t ;

/ Calculation of new values of phi and v /

yout [0]= yin [ 0]+ 1.0 /6 .0 ( k1 [0]+2 k2 [0]+2 k3 [0]+ k4 [ 0 ] ) ;

yout [1]= yin [ 1]+ 1.0 /6 .0 ( k1 [1]+2 k2 [1]+2 k3 [1]+ k4 [ 1 ] ) ;

}

14.7. PHYSICS PROJECT: THE PENDULUM 285

void pendelum : : rk4 ( )

{

/ We are using the fourth order Runge Kutta algorithm

We have to ca lcu late the parameters k1 , k2 , k3 , k4 for v and phi ,

so we use to arrays k1 [ 2] and k2 [ 2] for t h i s

k1 [ 0 ] , k2 [ 0] are the parameters for phi ,

k1 [ 1 ] , k2 [ 1] are the parameters for v

int i ;

double t_h ;

double yout [2] , y_h [ 2 ] ; / / k1 [2] , k2 [2] , k3 [2] , k4 [2] , y_k [2];

t_h =0;

y_h [0]= y [ 0 ] ; / / phi

y_h [1]= y [ 1 ] ; / / v

ofstream fout ( ) ;

fout . s e tf ( ios : : s c i e n t i f i c ) ;

fout . preci si o n (20) ;

for ( i =1; i <=n ; i ++){

rk4_step ( t_h , y_h , yout , delta_t _ ro of ) ;

fout << i delta _t << <<yout [0] << <<yout [1] < < ;

t_h+= d el t a_t _ro o f ;

y_h [0]= yout [ 0 ] ;

y_h [1]= yout [ 1 ] ;

}

fout . close ;

}

void pendelum : : asc ()

{

We are using the Runge Kutta algorithm with adaptive s t e p s i z e

control

according to " Numerical Recipes in C" , S . 5 7 4 f f .

At f i r s t we c alc ul ate y ( x+h ) using rk4 method => y1

Then we c a lc ul ate y ( x+h ) using two times rk4 method at x+h / 2 and x

+h => y2

The dif f e ren c e between these values is calle d " d elta " I f i t i s

smaller than a given value ,

286 CHAPTER 14. DIFFERENTIAL EQUATIONS

we calcu la t e y ( x+h ) by y2 + ( delta ) / 15 ( page 57 5 , Numerical R . )

I f delt a i s not smaller than . . . we ca lc ula te a new s tepsize using

h_new=( Safety ) h_old ( . . . / de lta ) ^ (0 .2 5) where " Safety " i s constant

( page 577 N.R . )

and s t a r t again with ca lc u la t in g y ( x+h ) . . .

int i ;

double t_h , h_alt , h_neu , hh , errmax ;

double yout [2] , y_h [2 ] , y_m [2] , y1 [2] , y2 [ 2 ] , d e lt a [ 2 ] , yscal [2] ;

const double eps =1.0 e 6;

const double saf et y =0.9;

const double errcon =6.0e 4;

const double ti ny =1.0e 30;

t_h =0;

y_h [0]= y [ 0 ] ; / / phi

y_h [1]= y [ 1 ] ; / / v

h_neu= d elt a_t_ roo f ;

ofstream fout ( ) ;

fout . s e tf ( ios : : s c i e n t i f i c ) ;

fout . preci si o n (20) ;

for ( i =0; i <=n ; i ++){

/ The error i s scaled against yscal

We use a yscal of the form yscal = fabs ( y [ i ]) + fabs (h

deri v a t i v es [ i ])

(N. R . page 567)

deri v a t i v es ( t_h , y_h , yout ) ;

yscal [0]= fabs (y [0] ) + fabs ( h_neu yout [0] ) + t iny ;

yscal [1]= fabs (y [1] ) + fabs ( h_neu yout [1] ) + t iny ;

/ the do while loop is used u n t i l the /

do{

/ Calculating y2 by two ha lf step s /

h_ al t=h_neu ;

hh= h_alt 0. 5;

rk4_step ( t_h , y_h , y_m , hh ) ;

rk4_step ( t_h+hh , y_m , y2 , hh ) ;

/ Calculating y1 by one normal step /

rk4_step ( t_h , y_h , y1 , h _alt ) ;

/ Now we have two values for phi and v at the time t_h + h in

y2 and y1

We can now cal cu la t e the de lt a for phi and v

14.7. PHYSICS PROJECT: THE PENDULUM 287

del t a [0]= fabs ( y1[0] y2 [0] ) ;

del t a [1]= fabs ( y1[1] y2 [1] ) ;

errmax =( d el t a [ 0 ] / yscal [0] > de l ta [ 1 ] / yscal [ 1 ] ? d e lta [ 0 ] / yscal

[ 0 ] : de l ta [1] / yscal [1] ) ;

/ We scale delta against the constant yscal

Then we take the bigges t one and c all i t errmax /

errmax =( double ) errmax / eps ;

/ We di vide errmax by eps and have only /

h_neu= saf ety h_ al t exp ( 0.25 log ( errmax ) ) ;

}while ( errmax >1.0) ;

/ Now we are outsi de the do while loop and have a d elta which i s

small enough

So we can c al cu lat e the new values of phi and v

yout [0]= y_h [0]+ d el t a [ 0 ] / 1 5 . 0 ;

yout [1]= y_h [1]+ d el t a [ 1 ] / 1 5 . 0 ;

fout <<( double ) ( t_h+h_alt ) / omega_0 << <<yout [0] << <<yout

[1] < < ;

/ / Calculating of the new s t e p s i z e

h_neu =( errmax > errcon ? sa fet y h _a lt exp ( 0.20 log ( errmax ) )

: 4 . 0 h _alt ) ;

y_h [0]= yout [ 0 ] ;

y_h [1]= yout [ 1 ] ;

t_h+=h_neu ;

}

int main ()

{

pendelum t e s t c a s e ;

t e s t c a se . i n i t i a l i s e () ;

t e s t c a se . e uler () ;

t e s t c a se . euler_cromer ( ) ;

t e s t c a se . midpoint () ;

t e s t c a se . e ul er _r ic ha rdso n () ;

t e s t c a se . ha lf_st ep () ;

t e s t c a se . rk2 ( ) ;

t e s t c a se . rk4 ( ) ;

return 0 ;

} / / end of main fun ction

288 CHAPTER 14. DIFFERENTIAL EQUATIONS

14.8 Physics project: Period doubling and chaos

in preparation

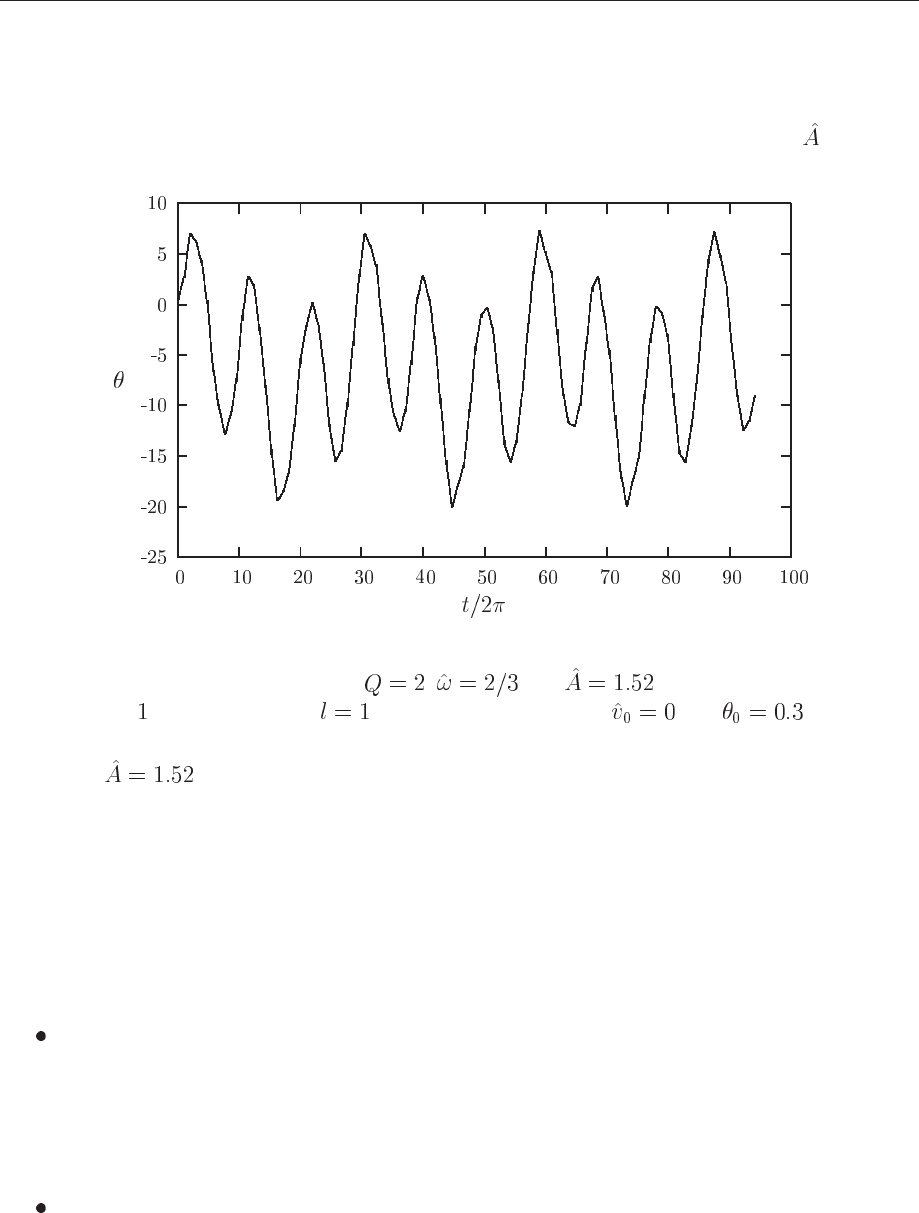
In Fig. ?? we have kept the same constants as in the previous section except for

which we

Figure 14.10: Phase-space curve with , and . The mass of the pendulum

is set equal to kg and its length m. The inital velocity is and .

now set to .

14.9 Physics Project: studies of neutron stars

In the pendulum example we rewrote the equations as two differential equations in terms of so-

called dimensionless variables. One should always do that. There are at least two good reasons

for doing this.

By rewriting the equations as dimensionless ones, the program will most likely be easier to

read, with hopefully a better possibility of spotting eventual errors. In addtion, the various

constants which are pulled out of the equations in the process of rendering the equations

dimensionless, are reintroduced at the end of the calculation. If one of these constants is

not correctly deﬁned, it is easier to spot an eventual error.

In many physics applications, variables which enter a differential equation, may differ by

orders of magnitude. If we were to insist on not using dimensionless quantities, such

differences can cause serious problems with respect to loss of numerical precision.