Hjorth-Jensen M. Computational Physics

Подождите немного. Документ загружается.

15.6. ALGORITHM FOR SOLVING SCHRÖDINGER’S EQUATION 299

} / / End : funtio n plot ( )

Chapter 16

Partial differential equations

16.1 Introduction

In the Natural Sciences we often encounter problems with many variables constrained by bound-

ary conditions and initial values. Many of these problems can be modelled as partial differential

equations. One case which arises in many situations is the so-called wave equation whose one-

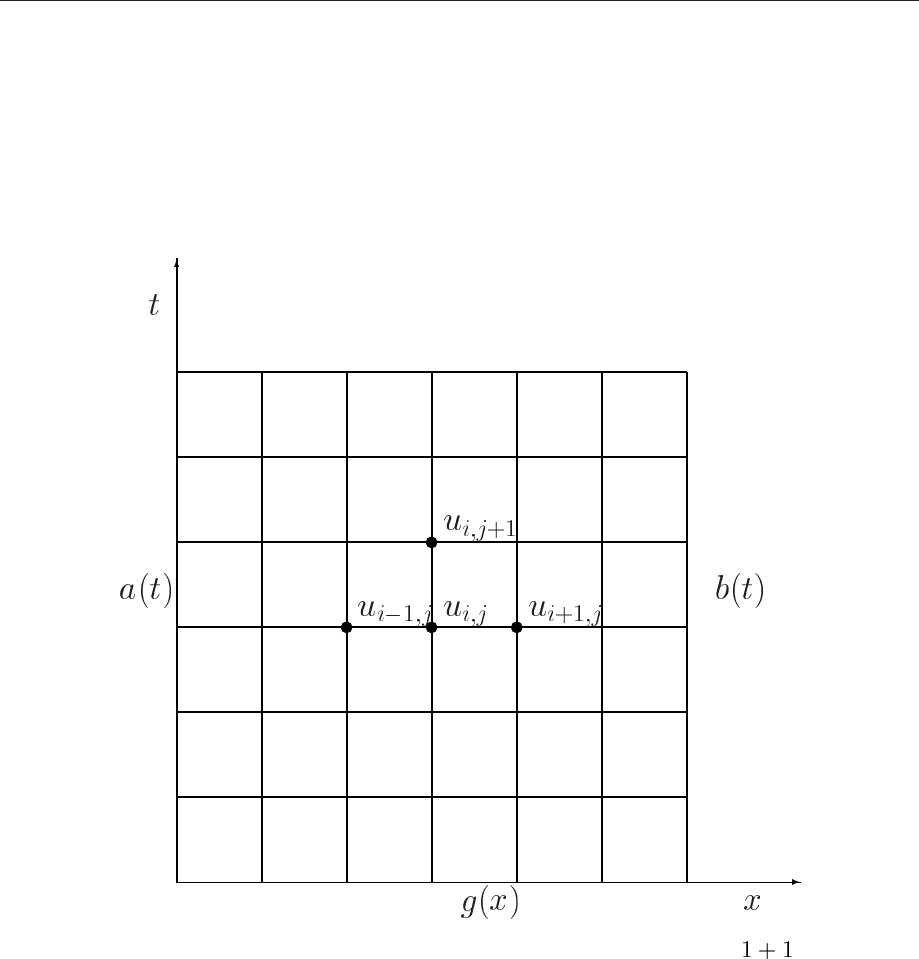
dimensional form reads

(16.1)

where

is a constant. Familiar situations which this equation can model are waves on a string,

pressure waves, waves on the surface of a fjord or a lake, electromagnetic waves and sound waves

to mention a few. For e.g., electromagnetic waves the constant

, with the speed of light.

It is rather straightforward to extend this equation to two or three dimension. In two dimensions

we have

(16.2)

In Chapter 10 we saw another case of a partial differential equation widely used in the Nat-

ural Sciences, namely the diffusion equation whose one-dimensional version we derived from a

Markovian random walk. It reads

(16.3)

and

is in this case called the diffusion constant. It can be used to model a wide selection of

diffusion processes, from molecules to the diffusion of heat in a given material.

Another familiar equation from electrostatics is Laplace’s equation, which looks similar to

the wave equation in Eq. (16.1) except that we have set

(16.4)

or if we have a ﬁnite electric charge represented by a charge density

we have the familiar

Poisson equation

(16.5)

301

302 CHAPTER 16. PARTIAL DIFFERENTIAL EQUATIONS

However, although parts of these equation look similar, we will see below that different solu-

tion strategies apply. In this chapter we focus essentially on so-called ﬁnite difference schemes

and explicit and implicit methods. The more advanced topic of ﬁnite element methods is rele-

gated to the part on advanced topics.

A general partial differential equation in

-dimensions (with standing for the spatial

coordinates and and for time) reads

(16.6)

and if we set

(16.7)

we recover the -dimensional diffusion equation which is an example of a so-called parabolic

partial differential equation. With

(16.8)

we get the

-dim wave equation which is an example of a so-called hyperolic PDE, where

more generally we have . For we obtain a so-called ellyptic PDE, with the

Laplace equation in Eq. (16.4) as one of the classical examples. These equations can all be easily

extended to non-linear partial differential equations and

dimensional cases.

The aim of this chapter is to present some of the most familiar difference methods and their

eventual implementations.

16.2 Diffusion equation

The let us assume that the diffusion of heat through some material is proportional with the tem-

perature gradient

and using conservation of energy we arrive at the diffusion equation

(16.9)

where

is the speciﬁc heat and the density of the material. Here we let the density be repre-

sented by a constant, but there is no problem introducing an explicit spatial dependence, viz.,

(16.10)

Setting all constants equal to the diffusion constant , i.e.,

(16.11)

we arrive at

(16.12)

16.2. DIFFUSION EQUATION 303

Specializing to the -dimensional case we have

(16.13)

We note that the dimension of

is time/length . Introducing the dimensional variables

we get

(16.14)

and since

is just a constant we could deﬁne or use the last expression to deﬁne a

dimensionless time-variable

. This yields a simpliﬁed diffusion equation

(16.15)

It is now a partial differential equation in terms of dimensionless variables. In the discussion

below, we will however,for the sake of notational simplicity replace

and . Moreover,

the solution to -dimensional partial differential equation is replaced by .

16.2.1 Explicit scheme

In one dimension we have thus the following equation

(16.16)

(16.17)

with initial conditions, i.e., the conditions at

(16.18)

with

the length of the -region of interest. The boundary conditions are

(16.19)

and

(16.20)

where

and are two functions which depend on time only, while depends only on

the position

. Our next step is to ﬁnd a numerical algorithm for solving this equation. Here

we recur to our familiar equal-step methods discussed in Chapter 3 and introduce different step

lengths for the space-variable

and time through the step length for

(16.21)

304 CHAPTER 16. PARTIAL DIFFERENTIAL EQUATIONS

and the time step length . The position after steps and time at time-step are now given by

(16.22)

If we then use standard approximations for the derivatives we obtain

(16.23)

with a local approximation error

and

(16.24)

(16.25)

with a local approximation error . Our approximation is to higher order in the coordi-

nate space. This can be justiﬁed since in most cases it is the spatial dependence which causes

numerical problems. These equations can be further simpliﬁed as

(16.26)

and

(16.27)

The one-dimensional diffusion equation can then be rewritten in its discretized version as

(16.28)

Deﬁning results in the explicit scheme

(16.29)

Since all the discretized initial values

(16.30)

are known, then after one time-step the only unknown quantity is

which is given by

(16.31)

We can then obtain using the previously calculated values and the boundary conditions

and . This algorithm results in a so-called explicit scheme, since the next functions is

16.2. DIFFUSION EQUATION 305

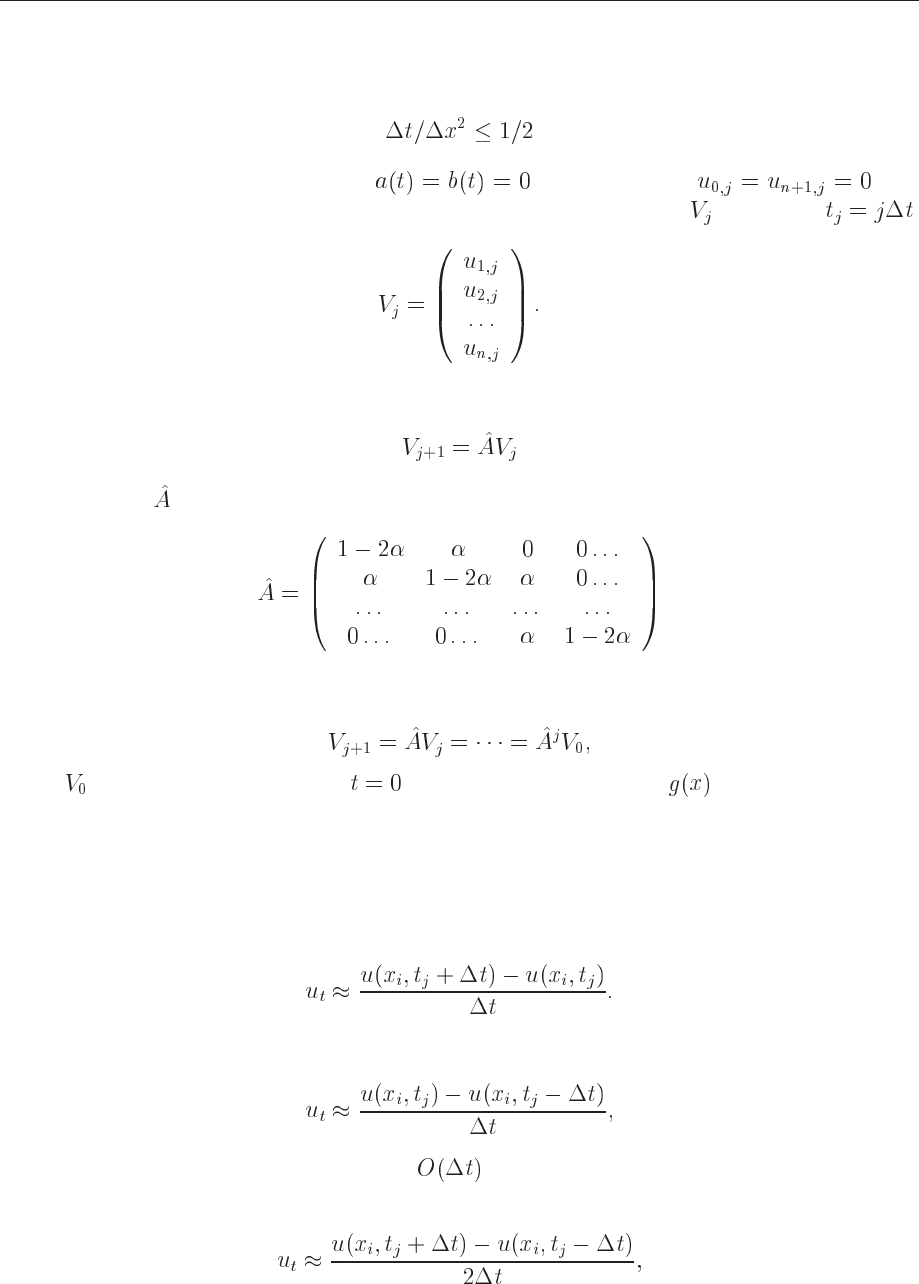
Figure 16.1: Discretization of the integration area used in the solution of the -dimensional

diffusion equation.

306 CHAPTER 16. PARTIAL DIFFERENTIAL EQUATIONS

explicitely given by Eq. (16.29). The procedure is depicted in Fig. 16.2.1. The explicit scheme,

although being rather simple to implement has a very weak stability condition given by

(16.32)

We will now specialize to the case

which results in . We

can then reformulate our partial differential equation through the vector at the time

(16.33)

This results in a matrix-vector multiplication

(16.34)

with the matrix

given by

(16.35)

which means we can rewrite the original partial differential equation as a set of matrix-vector

multiplications

(16.36)

where

is the initial vector at time deﬁned by the initial value .

16.2.2 Implicit scheme

In deriving the equations for the explicit scheme we started with the so-called forward formula

for the ﬁrst derivative, i.e., we used the discrete approximation

(16.37)

However, there is nothing which hinders us from using the backward formula

(16.38)

still with a truncation error which goes like

. We could also have used a midpoint approx-

imation for the ﬁrst derivative, resulting in

(16.39)

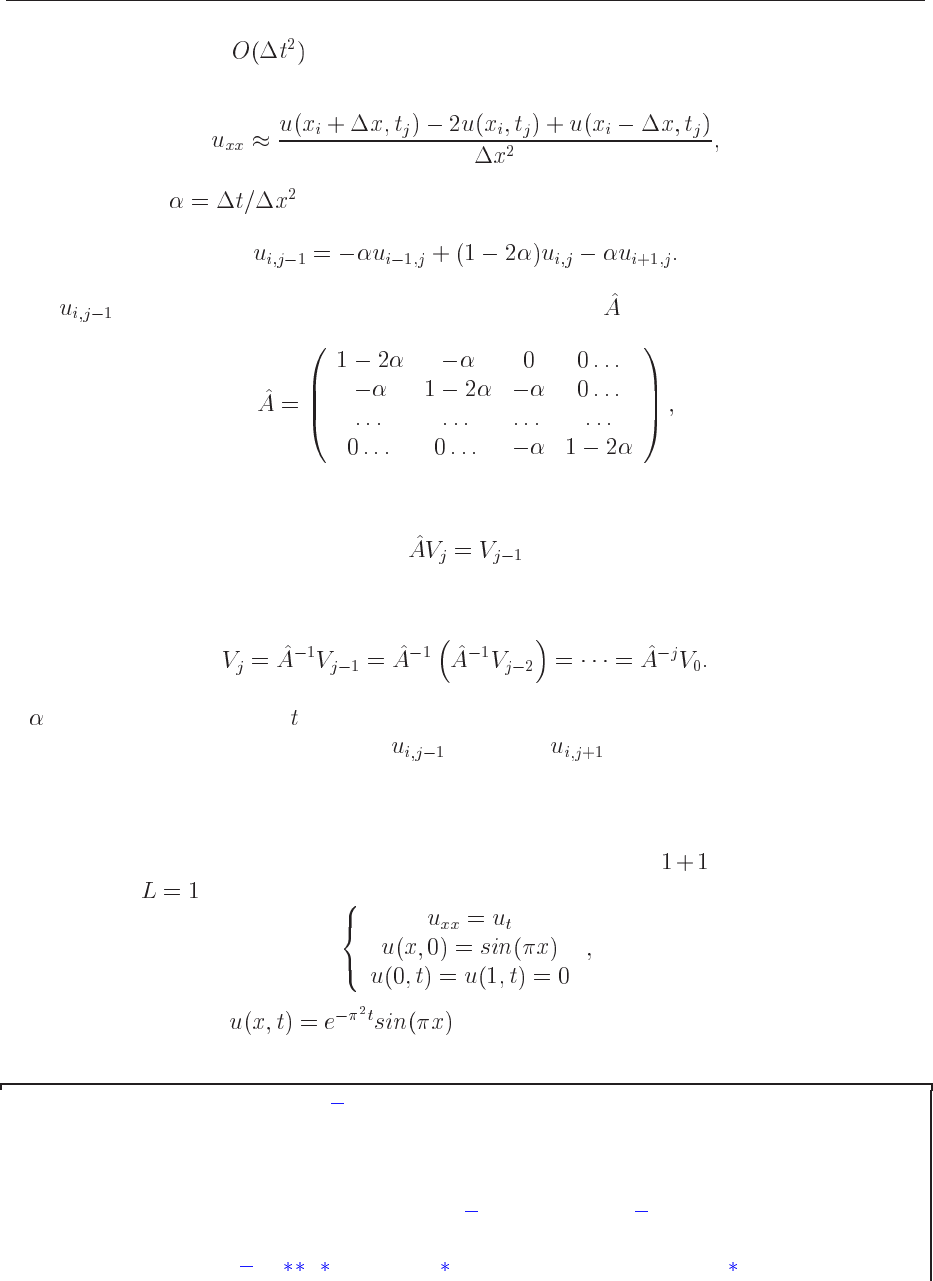
16.2. DIFFUSION EQUATION 307

with a truncation error . Here we will stick to the backward formula and come back to

the later below. For the second derivative we use however

(16.40)

and deﬁne again

. We obtain now

(16.41)

Here

is the only unknown quantity. Deﬁning the matrix

(16.42)

we can reformulate again the problem as a matrix-vector multiplication

(16.43)

meaning that we can rewrite the problem as

(16.44)

does not depend on time , we need to invert a matrix only once. This is an implicit scheme

since it relies on determining the vector instead of

16.2.3 Program example

Here we present a simple Fortran90 code which solves the following

-dimensional diffusion

problem with

(16.45)

with the exact solution

programs/chap16/program1.f90

! Program to solve the 1 dim heat equation using

! matrix invers io n . The i n i t i a l condit ions are given by

! u( xmin , t )=u(xmax , t ) =0 ang u ( x , 0 ) = f ( x ) ( user provided f unct ion )

! I n i t i a l c onditions are read in by the functi on i n i t i a l i s e

! such as number of st ep s in the x direction , t direction ,

! xmin and xmax . For xmin = 0 and xmax = 1 , the exact s o lu ti o n

! is u ( x , t ) = exp( pi 2 x ) sin ( pi x ) with f ( x ) = sin ( pi x )

308 CHAPTER 16. PARTIAL DIFFERENTIAL EQUATIONS

! Note the s t ru ctur e of th i s module , i t contains various

! subrou tines for i n i t i a l i s a t i o n of the problem and sol uti on

! of the PDE with a given i n i t i a l f unct io n for u ( x , t )

MODULE one_dim_heat_equation

DOUBLE PRECISION, PRIVATE : : xmin , xmax , k

INTEGER, PRIVATE : : m , ndim

CONTAINS

SUBROUTINE i n i t i a l i s e

IMPLICIT NONE

WRITE( , ) ’ read in number of mesh points in x ’

READ( , ) ndim

WRITE( , ) ’ read in xmin and xmax ’

READ( , ) xmin , xmax

WRITE( , ) ’ read in number of time steps ’

READ( , ) m

WRITE( , ) ’ read in s tep s i z e in t ’

READ( , ) k

END SUBROUTINE i n i t i a l i s e

SUBROUTINE solve_1dim_equation ( func )

DOUBLE PRECISION : : h , factor , det , t , pi

INTEGER : : i , j , l

DOUBLE PRECISION, ALLOCATABLE, DIMENSION( : , : ) : : a

DOUBLE PRECISION, ALLOCATABLE, DIMENSION( : ) : : u , v

INTERFACE

DOUBLE PRECISION FUNCTION func ( x )

IMPLICIT NONE

DOUBLE PRECISION, INTENT( IN) : : x

END FUNCTION func

END INTERFACE

! defi ne the step s i ze

h = ( xmax xmin ) /FLOAT( ndim +1)

f act o r = k / h / h

! al loc ate space for the vectors u and v and the matrix a

ALLOCATE ( a ( ndim , ndim ) )

ALLOCATE ( u ( ndim ) , v ( ndim ) )

pi = ACOS( 1.)

DO i =1 , ndim

v( i ) = func ( pi i h )