Hjorth-Jensen M. Computational Physics

Подождите немного. Документ загружается.

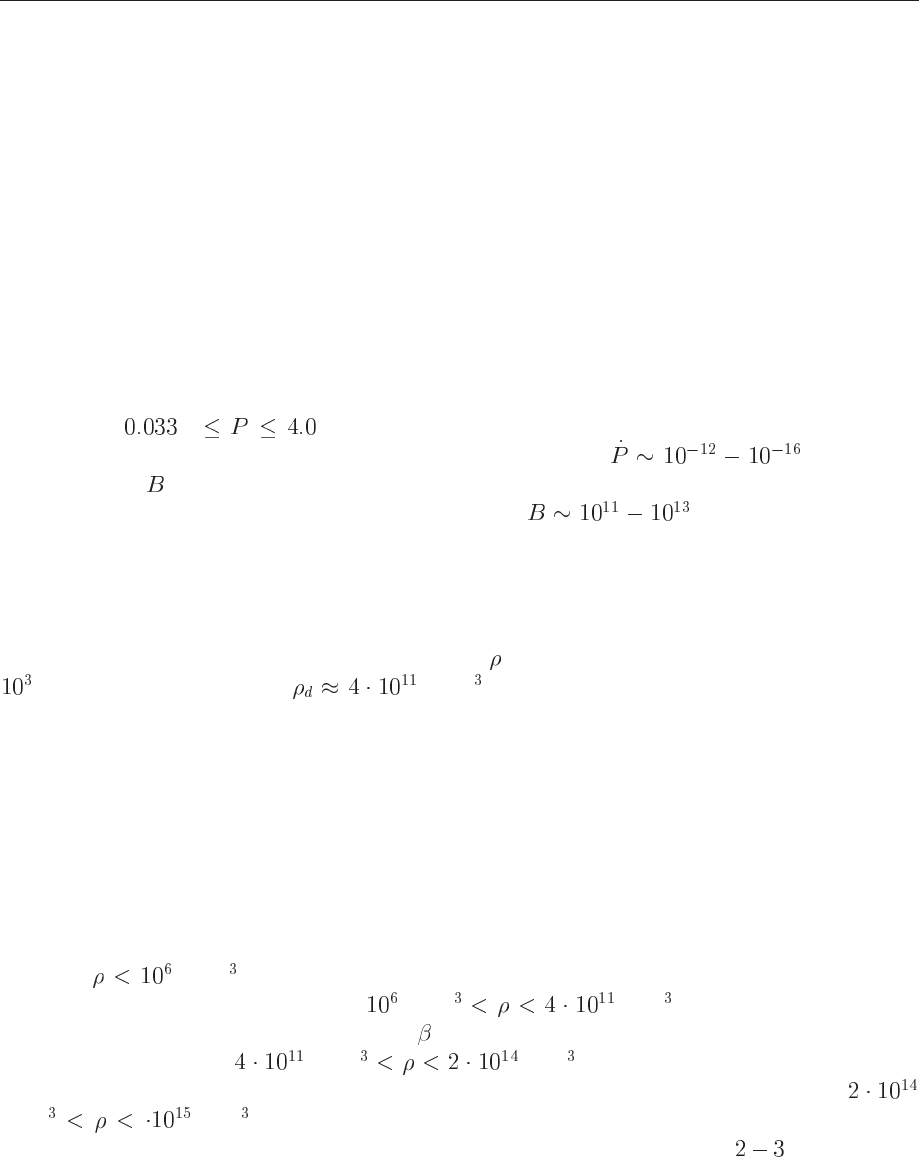
14.9. PHYSICS PROJECT: STUDIES OF NEUTRON STARS 289

An example which demonstrates these features is the set of equations for gravitational equi-

librium of a neutron star. We will not solve these equations numerically here, rather, we will

limit ourselves to merely rewriting these equations in a dimensionless form.

14.9.1 The equations for a neutron star

The discovery of the neutron by Chadwick in 1932 prompted Landau to predict the existence

of neutron stars. The birth of such stars in supernovae explosions was suggested by Baade

and Zwicky 1934. First theoretical neutron star calculations were performed by Tolman, Op-

penheimer and Volkoff in 1939 and Wheeler around 1960. Bell and Hewish were the ﬁrst to

discover a neutron star in 1967 as a radio pulsar. The discovery of the rapidly rotating Crab pul-

sar ( rapidly rotating neutron star) in the remnant of the Crab supernova observed by the chinese

in 1054 A.D. conﬁrmed the link to supernovae. Radio pulsars are rapidly rotating with periods

in the range s s. They are believed to be powered by rotational energy loss

and are rapidly spinning down with period derivatives of order

. Their high

magnetic ﬁeld leads to dipole magnetic braking radiation proportional to the magnetic ﬁeld

squared. One estimates magnetic ﬁelds of the order of G. The total number of

pulsars discovered so far has just exceeded 1000 before the turn of the millenium and the number

is increasing rapidly.

The physics of compact objects like neutron stars offers an intriguing interplay between nu-

clear processes and astrophysical observables. Neutron stars exhibit conditions far from those

encountered on earth; typically, expected densities

of a neutron star interior are of the order of

or more times the density g/cm at ’neutron drip’, the density at which nuclei

begin to dissolve and merge together. Thus, the determination of an equation of state (EoS) for

dense matter is essential to calculations of neutron star properties. The EoS determines prop-

erties such as the mass range, the mass-radius relationship, the crust thickness and the cooling

rate. The same EoS is also crucial in calculating the energy released in a supernova explosion.

Clearly, the relevant degrees of freedom will not be the same in the crust region of a neutron

star, where the density is much smaller than the saturation density of nuclear matter, and in the

center of the star, where density is so high that models based solely on interacting nucleons are

questionable. Neutron star models including various so-called realistic equations of state result

in the following general picture of the interior of a neutron star. The surface region, with typical

densities

g/cm , is a region in which temperatures and magnetic ﬁelds may affect the

equation of state. The outer crust for

g/cm g/cm is a solid region where a

Coulomb lattice of heavy nuclei coexist in -equilibrium with a relativistic degenerate electron

gas. The inner crust for

g/cm g/cm consists of a lattice of neutron-rich

nuclei together with a superﬂuid neutron gas and an electron gas. The neutron liquid for

g/cm g/cm contains mainly superﬂuid neutrons with a smaller concentration of

superconducting protons and normal electrons. At higher densities, typically

times nuclear

matter saturation density, interesting phase transitions from a phase with just nucleonic degrees

of freedom to quark matter may take place. Furthermore, one may have a mixed phase of quark

and nuclear matter, kaon or pion condensates, hyperonic matter, strong magnetic ﬁelds in young

stars etc.

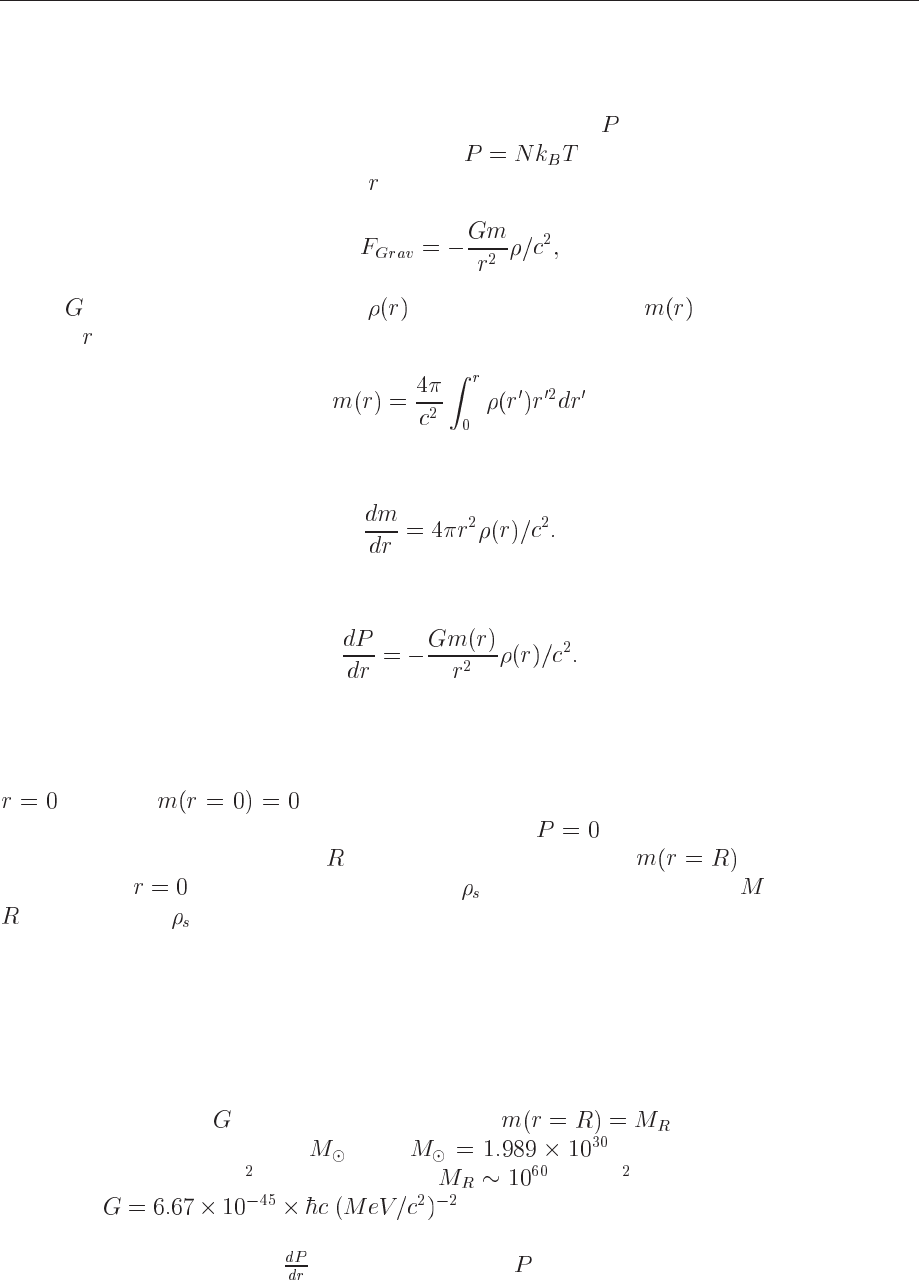
290 CHAPTER 14. DIFFERENTIAL EQUATIONS

14.9.2 Equilibrium equations

If the star is in thermal equilibrium, the gravitational force on every element of volume will be

balanced by a force due to the spacial variation of the pressure . The pressure is deﬁned by the

equation of state (EoS), recall e.g., the ideal gas . The gravitational force which acts

on an element of volume at a distance is given by

(14.88)

where

is the gravitational constant, is the mass density and is the total mass inside

a radius

. The latter is given by

(14.89)

which gives rise to a differential equation for mass and density

(14.90)

When the star is in equilibrium we have

(14.91)

The last equations give us two coupled ﬁrst-order differential equations which determine the

structure of a neutron star when the EoS is known.

The initial conditions are dictated by the mass being zero at the center of the star, i.e., when

, we have . The other condition is that the pressure vanishes at the surface

of the star. This means that at the point where we have

in the solution of the differential

equations, we get the total radius of the star and the total mass . The mass-energy

density when is called the central density . Since both the ﬁnal mass and total radius

will depend on , a variation of this quantity will allow us to study stars with different masses

and radii.

14.9.3 Dimensionless equations

When we now attempt the numerical solution, we need however to rescale the equations so

that we deal with dimensionless quantities only. To understand why, consider the value of the

gravitational constant

and the possible ﬁnal mass . The latter is normally of

the order of some solar masses

, with Kg. If we wish to translate the

latter into units of MeV/c , we will have that MeV/c . The gravitational constant is

in units of

. It is then easy to see that including the relevant

values for these quantities in our equations will most likely yield large numerical roundoff errors

when we add a huge number to a smaller number in order to obtain the new pressure. We

14.9. PHYSICS PROJECT: STUDIES OF NEUTRON STARS 291

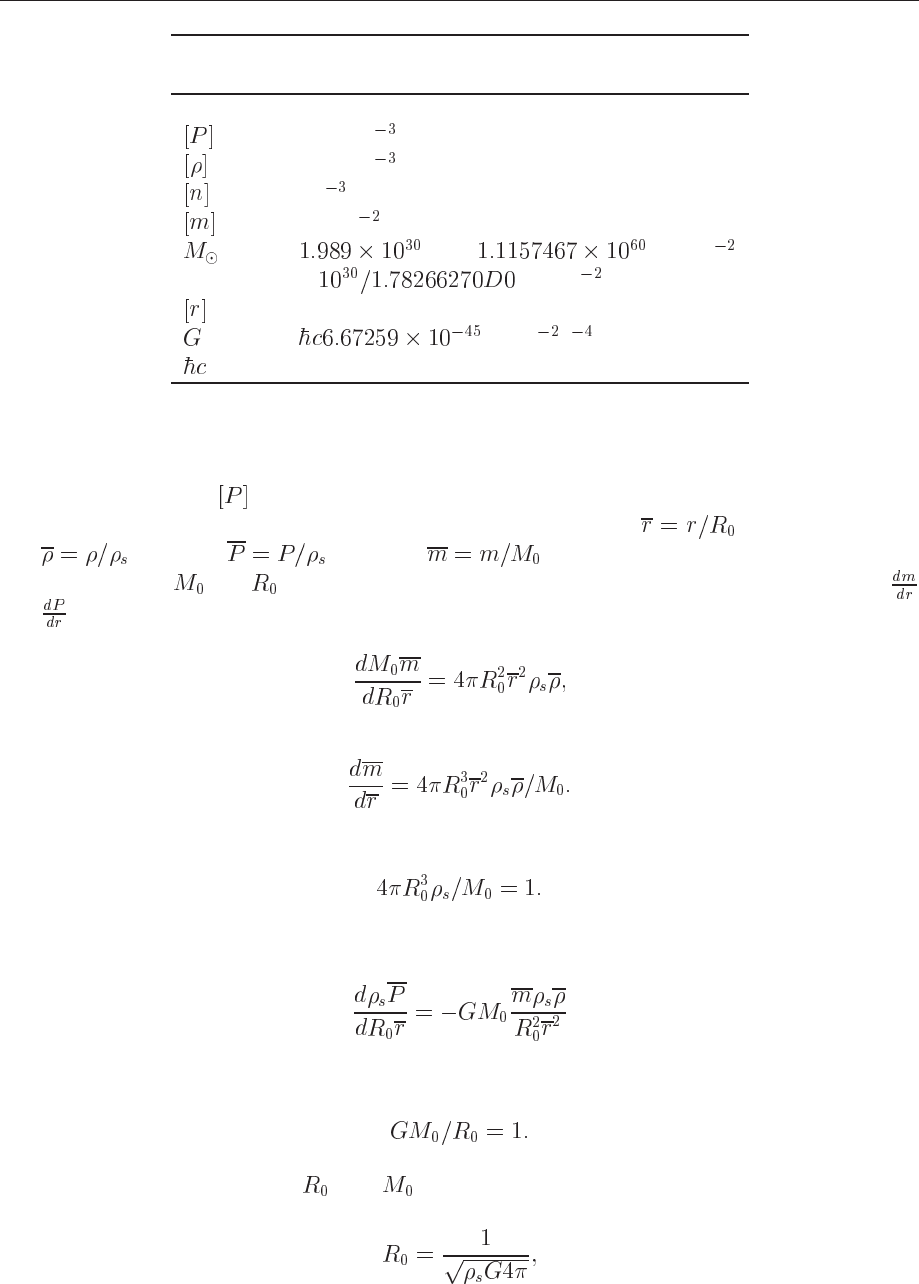
Quantity Units

MeVfm

MeVc

Kg= MeVc

1 Kg = MeVc

MeV c

197.327 MeVfm

list here the units of the various quantities and in case of physical constants, also their values. A

bracketed symbol like

stands for the unit of the quantity inside the brackets.

We introduce therefore dimensionless quantities for the radius

, mass-energy den-

sity , pressure and mass .

The constants

and can be determined from the requirements that the equations for

and should be dimensionless. This gives

(14.92)

yielding

(14.93)

If these equations should be dimensionless we must demand that

(14.94)

Correspondingly, we have for the pressure equation

(14.95)

and since this equation should also be dimensionless, we will have

(14.96)

This means that the constants and which will render the equations dimensionless are

given by

(14.97)

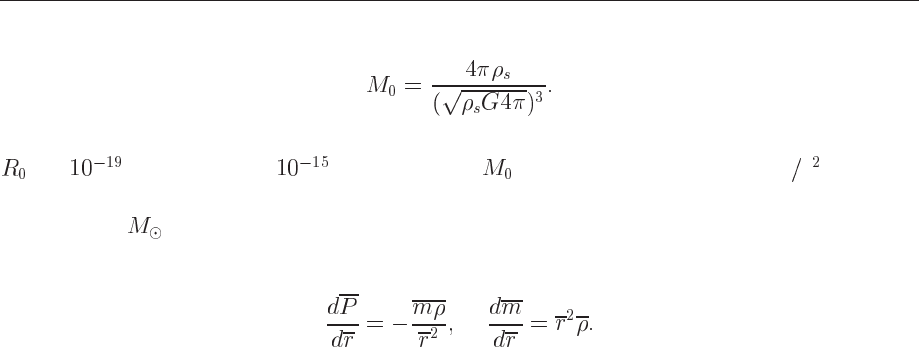
292 CHAPTER 14. DIFFERENTIAL EQUATIONS

and

(14.98)

However, since we would like to have the radius expressed in units of 10 km, we should multiply

by , since 1 fm = m. Similarly, will come in units of MeV c , and it is

convenient therefore to divide it by the mass of the sun and express the total mass in terms of

solar masses

The differential equations read then

(14.99)

14.9.4 Program and selected results

in preparation

14.10 Physicsproject: Systemsof linear differentialequations

in preparation

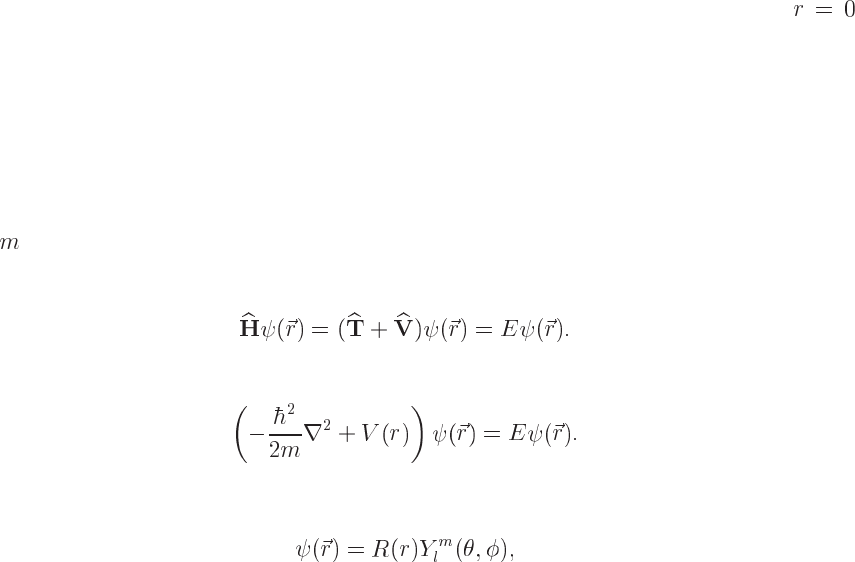
Chapter 15

Two point boundary value problems.

15.1 Introduction

This chapter serves as an intermediate step to the next chapter on partial differential equations.

Partial differential equations involve both boundary conditions and differential equations with

functions depending on more than one variable. Here we focus on the problem of boundary

conditions with just one variable. When diffential equations are required to satify boundary

conditions at more than one value of the independent variable, the resulting problem is called

two point boundary value problem

. As the terminology indicates, the most common case by

far is when boundary conditions are supposed to be satiﬁed at two points - usually the starting

and ending values of the integration. The Schrödinger equation is an important example of such

a case. Here the eigenfunctions are restricted to be ﬁnite everywhere (in particular at

)

and for bound states the functions must go to zero at inﬁnity. In this chapter we will discuss the

solution of the one-particle Schödinger equation and apply the method to the hydrogen atom.

15.2 Schrödinger equation

We discuss the numerical solution of the Schrödinger equation for the case of a particle with

mass

moving in a spherical symmetric potential.

The initial eigenvalue equation reads

(15.1)

In detail this gives

(15.2)

The eigenfunction in spherical coordinates takes the form

(15.3)

293

294 CHAPTER 15. TWO POINT BOUNDARY VALUE PROBLEMS.

and the radial part is a solution to

(15.4)

Then we substitute and obtain

(15.5)

We introduce a dimensionless variable where is a constant with dimension length

and get

(15.6)

In our case we are interested in attractive potentials

(15.7)

where

and analyze bound states where . The ﬁnal equation can be written as

(15.8)

where

(15.9)

15.3 Numerov’s method

Eq. (15.8) is a second order differential equation without any ﬁrst order derivatives. Numerov’s

method is designed to solve such an equation numerically, achieving an extra order of precision.

Let us start with the Taylor expansion of the wave function

(15.10)

where is a shorthand notation for the nth derivative . Because the corresponding

Taylor expansion of

has odd powers of appearing with negative signs, all odd powers

cancel when we add and

(15.11)

15.4. SCHRÖDINGER EQUATION FOR A SPHERICAL BOX POTENTIAL 295

Then we obtain

(15.12)

To eliminate the fourth-derivativeterm we apply the operator

to Eq. (15.8) and obtain

a modiﬁed equation

(15.13)

In this expression the

terms cancel. To treat the general dependence of we approxi-

mate the second derivative of by

(15.14)

and the following numerical algorithm is obtained

(15.15)

where

, and etc.

15.4 Schrödinger equation for a spherical box potential

Let us now specify the spherical symmetric potential to

for (15.16)

and choose

. Then

for (15.17)

The eigenfunctions in Eq. (15.2) are subject to conditions which limit the possible solutions. Of

importance for the present example is that

must be ﬁnite everywhere and must

be ﬁnite. The last condition means that for . These conditions imply that

must be ﬁnite at and for .

15.4.1 Analysis of

For small Eq. (15.8) reduces to

(15.18)

296 CHAPTER 15. TWO POINT BOUNDARY VALUE PROBLEMS.

with solutions or . Since the ﬁnal solution must be ﬁnite everywhere we

get the condition for our numerical solution

for small (15.19)

15.4.2 Analysis of

for

For large Eq. (15.8) reduces to

(15.20)

with solutions

and the condition for large means that our numerical solution

must satisfy

for large (15.21)

15.5 Numerical procedure

The eigenvalue problem in Eq. (15.8) can be solved by the so-called shooting methods. In order

to ﬁnd a bound state we start integrating, with a trial negative value for the energy, from small

values of the variable

, usually zero, and up to some large value of . As long as the potential

is signiﬁcantly different from zero the function oscillates. Outside the range of the potential the

function will approach an exponential form. If we have chosen a correct eigenvalue the function

decreases exponetially as

. However, due to numerical inaccuracy the solution will

contain small admixtures of the undesireable exponential growing function . The

ﬁnal solution will then become unstable. Therefore, it is better to generate two solutions, with

one starting from small values of

and integrate outwards to some matching point .

We call that function . The next solution is then obtained by integrating from some

large value

where the potential is of no importance, and inwards to the same matching point

. Due to the quantum mechanical requirements the logarithmic derivative at the matching

point should be well deﬁned. We obtain the following condition

at (15.22)

We can modify this expression by normalizing the function

. Then

Eq. (15.22) becomes

at (15.23)

For an arbitary value of the eigenvalue Eq. (15.22) will not be satisﬁed. Thus the numerical

procedure will be to iterate for different eigenvalues until Eq. (15.23) is satisﬁed.

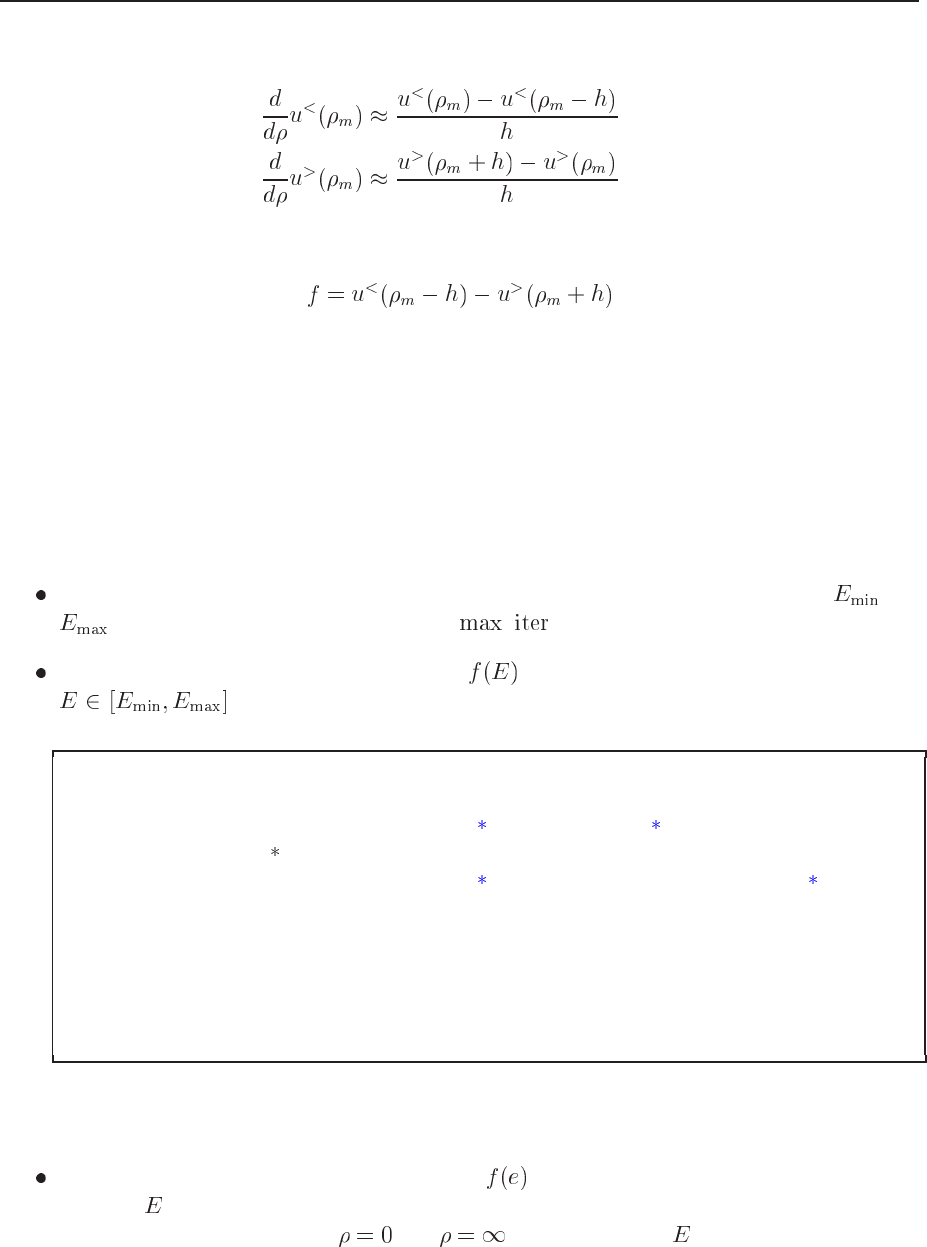
15.6. ALGORITHM FOR SOLVING SCHRÖDINGER’S EQUATION 297

We can calculate the ﬁrst order derivatives by

(15.24)

Thus the criterium for a proper eigenfunction will be

(15.25)

15.6 Algorithm for solving Schrödinger’s equation

of the solution. Here we outline the solution of Schrödinger’s equation as a common differential

equation but with boundary conditions. The method combines shooting and matching. The

shooting part involves a guess on the exact eigenvalue. This trial value is then combined with a

standard method for root searching, e.g., the secant or bisection methods discussed in chapter 8.

The algorithm could then take the following form

Initialise the problem by choosing minimum and maximum values for the energy, and

, the maximum number of iterations _ and the desired numerical precision.

Search then for the roots of the function , where the root(s) is(are) in the interval

using e.g., the bisection method. The pseudocode for such an approach

can be written as

do {

i ++;

e = ( e_min+e_max ) / 2 . ; / bi s ecti o n /

i f ( f ( e ) f ( e_max ) > 0 ) {

e_max = e ; / change search i n t e r v a l /

}

else {

e_min = e ;

}

} while ( ( fabs ( f ( e ) > convergence_test ) ! ! ( i <=

max_it erations ) )

The use of a root-searching method forms the shooting part of the algorithm. We have

however not yet speciﬁed the matching part.

The matching part is given by the function which receives as argument the present

value of

. This function forms the core of the method and is based on an integration of

Schrödinger’s equation from and . If our choice of satisﬁes Eq. (15.25) we

have a solution. The matching code is given below.

298 CHAPTER 15. TWO POINT BOUNDARY VALUE PROBLEMS.

The function above receives as input a guess for the energy. In the version implemented

below, we use the standard three-point formula for the second derivative, namely

We leave it as an exercise to the reader to implement Numerov’s algorithm.

/ /

/ / The f un ction

/ / f ( )

/ / c alc ula tes the wave func tion at fi x ed energy eigenvalue .

/ /

void f ( double step , int max_step , double energy , double w, double wf

)

{

int loop , loop_1 , match ;

double const s qr t _pi = 1.77245385091;

double fac , wwf , norm ;

/ / adding the energy guess to the array containing the p o t en tial

for ( loop = 0 ; loop <= max_step ; loop ++) {

w[ loop ] = (w[ loop ] energy ) step step + 2 ;

}

/ / i n teg r ati n g from large r values

wf [ max_step ] = 0 .0;

wf [ max_step 1 ] = 0.5 step step ;

/ / search for matching point

for ( loop = max_step 2; loop > 0; loop ) {

wf [ loop ] = wf [ loop + 1 ] w[ loop + 1] wf[ loop + 2 ] ;

i f (wf [ loop ] <= wf[ loop + 1 ] ) break ;

}

match = loop + 1 ;

wwf = wf [ match ] ;

/ / s t a r t int e gra t in g up to matching point from r =0

wf [ 0 ] = 0 . 0 ;

wf [ 1 ] = 0 . 5 step step ;

for ( loop = 2 ; loop <= match ; loop ++) {

wf [ loop ] = wf [ loop 1] w[ loop 1] wf [ loop 2];

i f ( fabs (wf [ loop ]) > INFINITY) {

for ( loop_1 = 0 ; loop_1 <= loop ; loop_1 ++) {

wf [ loop_1 ] / = INFINITY;

}

/ / now implement the t e s t of Eq . ( 1 0 . 2 5 )

return fabs (wf [ match 1] wf [ match +1]) ;