Hjorth-Jensen M. Computational Physics
Подождите немного. Документ загружается.

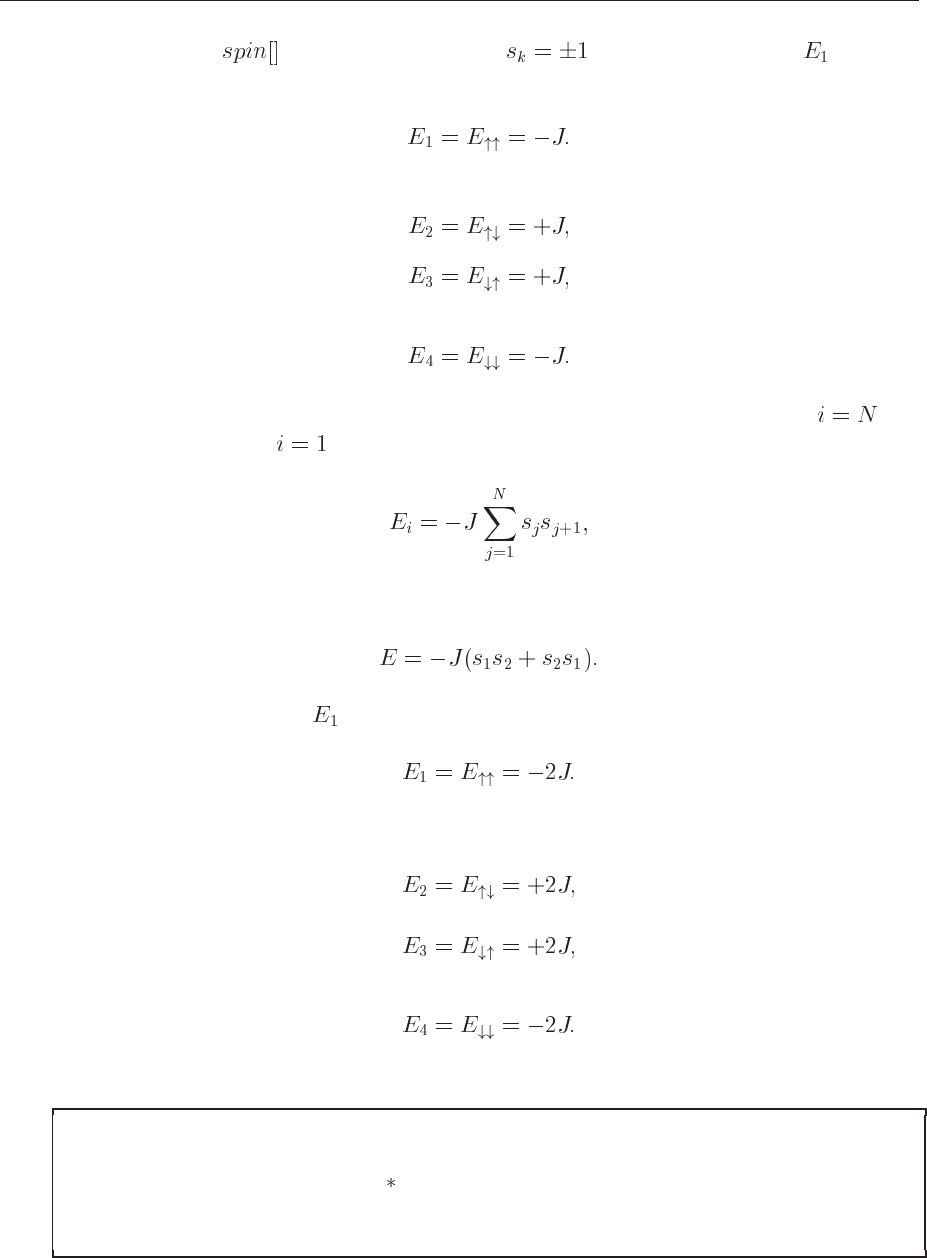
11.1. PHASE TRANSITIONS IN MAGNETIC SYSTEMS 189
where the vector contains the spin value . For the specific state , we have
chosen all spins up. The energy of this configuration becomes then
The other configurations give
and
2. We can also choose so-called periodic boundary conditions. This means that if , we
set the spin number to . In this case the energy for the one-dimensional lattice reads
(11.7)
and we obtain the following expression for the two-spin case
(11.8)
In this case the energy for
is different, we obtain namely
The other cases do also differ and we have
and
If we choose to use periodic boundary conditions we can code the above expression as
jm=N;
for ( j =1; j <=N ; j ++) {
energy += spin [ j ] spin [ jm ] ;
jm = j ;
}
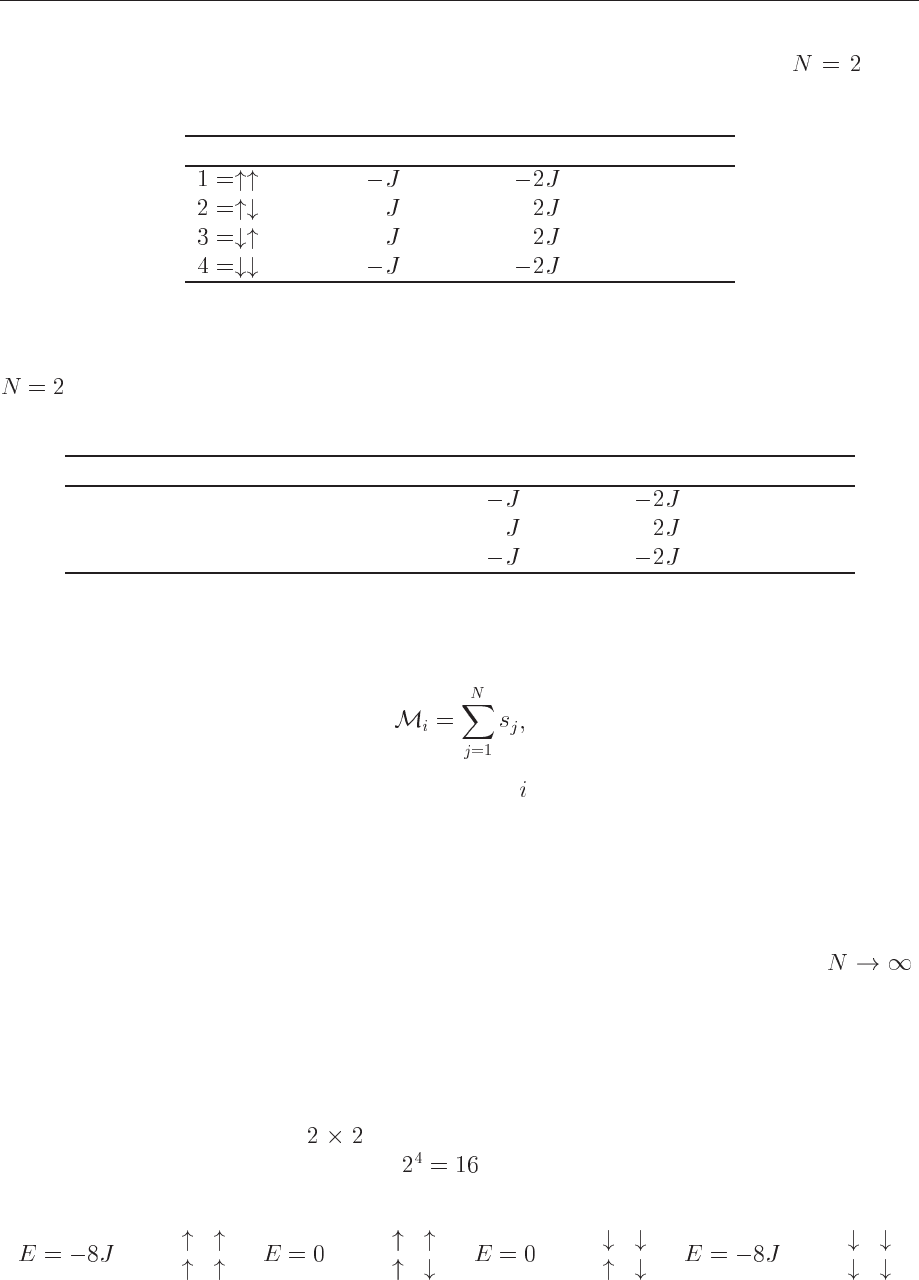
190 CHAPTER 11. MONTE CARLO METHODS IN STATISTICAL PHYSICS
Table 11.1: Energy and magnetization for the one-dimensional Ising model with spins
with free ends (FE) and periodic boundary conditions (PBC).
State Energy (FE) Energy (PBC) Magnetization
2
0
0
-2
Table 11.2: Degeneracy, energy and magnetization for the one-dimensional Ising model with
spins with free ends (FE) and periodic boundary conditions (PBC).
Number spins up Degeneracy Energy (FE) Energy (PBC) Magnetization
2 1 2
1 2
0
0 1 -2
The magnetization is however the same, defined as
(11.9)
where we sum over all spins for a given configuration
.
Table 11.1 lists the energy and magnetization for both free ends and periodic boundary con-
ditions.
We can reorganize Table 11.1 according to the number of spins pointing up, as shownin Table
11.2. It is worth noting that for small dimensions of the lattice, the energy differs depending on
whether we use periodic boundary conditions or fri ends. This means also that the partition
functions will be different, as discussed below. In the thermodynamic limit however,
,
the final results do not depend on the kind of boundary conditions we choose.
For a one-dimensional lattice with periodic boundary conditions, each spin sees two neigh-
bors. For a two-dimensional lattice each spin sees four neighboring spins. How many neighbors
does a spin see in three dimensions?
In a similar way, we could enumerate the number of states for a two-dimensional system
consisting of two spins, i.e., a
Ising model on a square lattice with periodic boundary
conditions. In this case we have a total of
states. Some examples of configurations with
their respective energies are listed here
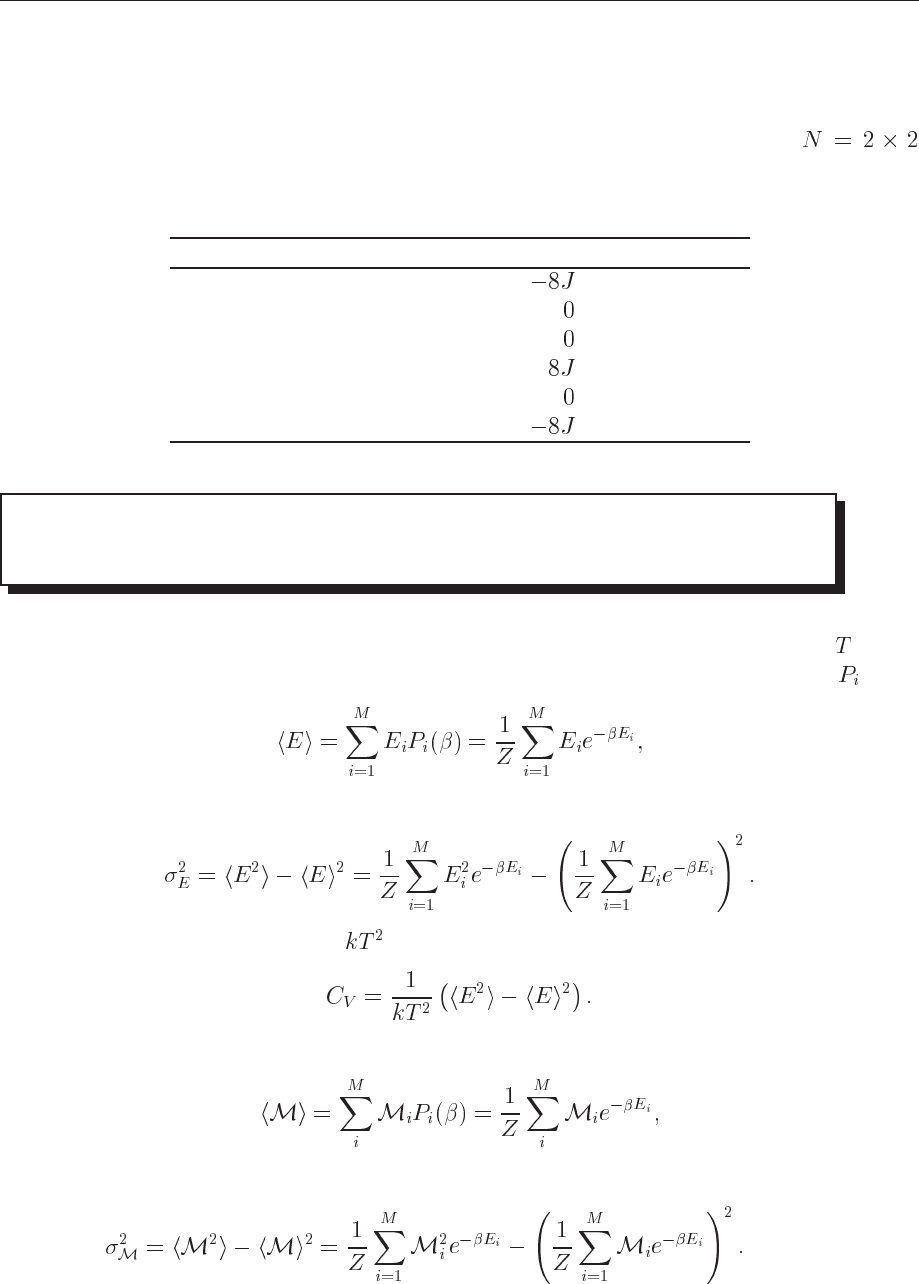
11.1. PHASE TRANSITIONS IN MAGNETIC SYSTEMS 191
In the Table 11.3 we group these configurations according to their total energy and magneti-
zation.
Table 11.3: Energy and magnetization for the two-dimensional Ising model with
spins with periodic boundary conditions.
Number spins up Degeneracy Energy Magnetization
4 1 4
3 4
2
2 4 0
2 2 0
1 4
-2
0 1 -4
Exercise 11.1
Convince yourself that the values listed in Table 11.3 are correct.
For a system described by the canonical ensemble, the energy is an expectation value since
we allow energy to be exchanged with the surroundings (a heat bath with temperature ). This
expectation value, the mean energy, can be calculated using the probability distribution as
(11.10)
with a corresponding variance defined as
(11.11)
If we divide the latter quantity with
we obtain the specific heat at constant volume
(11.12)
Using the same prescription, we can also evaluate the mean magnetization through
(11.13)
and the corresponding variance
(11.14)

192 CHAPTER 11. MONTE CARLO METHODS IN STATISTICAL PHYSICS
This quantity defines also the susceptibility
(11.15)
It is also possible to show that the partition function for the one-dimensional case for spins
with free ends is
(11.16)
If we use periodic boundary conditions it becomes
(11.17)
In the limit
the two results agree.
We can then calculate the mean energy with fri ends from the above formula or using
(11.18)
If we take our simple system with just two spins in one-dimension, we see immediately that
the above expression for the partition function is correct. Using the definition of the partition
function we have
(11.19)
If we take the limit
( ) and set , we obtain
(11.20)
which is the energy where all spins point in the same direction. At low
, the system tends
towards a state with the highest possible degree of order.
The specific heat in one-dimension with free ends is
(11.21)
Exercise 11.2
Calculate the exact partition function for a system of three spins with the one-
dimensional Ising model using both free ends and periodic boundary conditions.
For our two-dimensional lattice we obtain the following partition function
(11.22)
and mean energy
(11.23)

11.1. PHASE TRANSITIONS IN MAGNETIC SYSTEMS 193
The analytical expression for the Ising model in two dimensions was obtained in 1944 by the
Norwegian chemist Lars Onsager (Nobel prize in chemistry). The exact partition function for
spins is given by
(11.24)
with
(11.25)
and
(11.26)
Exercise 11.3
Calculate the heat capacity and the mean magnetization per spin for the
ising
model.
11.1.2 The Metropolis algorithm
The algorithm of choice for solving the Ising model is the approach proposed by Metropolis et
al. in 1953. As discussed in chapter ??, new configurations are generated from a previous one
using a transition probability which depends on the energy difference between the initial and
final states.
In our case we have as the Monte Carlo sampling function the probability for finding the
system in a state
given by
with energy , and is a normalization constant which defines the partition function
in the canonical ensemble. As discussed above
is difficult to compute since we need all states. In a calculation of the Ising model in two di-
mensions, the number of configurations is given by with the number of spins
for a lattice of length . Fortunately, the Metropolis algorithm considers only ratios between
probabilities and we do not need to compute the partition function at all. The algorithm goes as
follows
1. Establish an initial state with energy
by positioning yourself at a random position in the
lattice
2. Change the initial configuration by flipping e.g., one spin only. Compute the energy of this
trial state
.
3. Calculate
. The number of values is limited to five for the Ising model
in two dimensions, see the discussion below.

194 CHAPTER 11. MONTE CARLO METHODS IN STATISTICAL PHYSICS
4. If we accept the new configuration, meaning that the energy is lowered and we
are hopefully moving towards the energy minimum at a given temperature. Go to step 7.
5. If , calculate .
6. Compare with a random number . If
then accept the new configuration, else we keep the old configuration.
7. The next step is to update various expectations values.
8. The steps (2)-(7) are then repeated in order to obtain a sufficently good representation of
states.
9. Each time you sweep through the lattice, i.e., when you have summed over all spins, con-
stitutes what is called a Monte Carlo cyclus. You could think of one such cyclus as a
measurement. At the end, you should divide the various expectation values with the total
number of cycles. You can choose whether you wish to divide by the number of spins or
not. If you divide with the number of spins as well, your result for e.g., the energy is now
the energy per spin.
The implementation of this algorithm is given in the next section. In the calculation of the
energy difference from one spin configuration to the other, we will limit the change to the flipping
of one spin only. For the Ising model in two dimensions it means that there will only be a limited
set of values for
. Actually, there are only five possible values. To see this, select first a
random spin position and assume that this spin and its nearest neighbors are all pointing
up. The energy for this configuration is
. Now we flip this spin as shown below. The
energy of the new configuration is , yielding .
The four other possibilities are as follows
with ,

11.2. PROGRAM EXAMPLE 195
with ,
with and finally
with . This means in turn that we could construct an array which contains all values
of
before doing the Metropolis sampling. Else, we would have to evaluate the exponential
at each Monte Carlo sampling.
11.2 Program example
We list here an example of a C/C++-program which computes various thermodynamical prop-
erties of the Ising model in two dimensions You should especially pay attention to the function
Metropolis which implements the algorithm described in the previous subsection and the func-
tion
which calculates the energy difference between the previous state and the trial state
by flipping one spin.
The program is set up with dynamic memory allocation for the matrix which contains the
spin values at a position
. One could alternatively have used a fixed size for the matrices to
be used. But then one would need to recompile the program when larger systems are considered.
11.2.1 Program for the two-dimensional Ising Model
programs/chap11/program1.cpp
/
Program to solve the two dimensional Is ing model
The coupling constant J = 1
Boltzmann ’ s constant = 1 , temperature has thus dimension energy
Metropolis sampling i s used . Periodic boundary conditions .
/
#include < iostream >
#include < fstream >
#include < iomanip >
#include
using namespace std ;

196 CHAPTER 11. MONTE CARLO METHODS IN STATISTICAL PHYSICS
ofstream o f i l e ;
/ / inli ne fu nc tion for periodic boundary condition s
in line int per iodi c ( int i , int limit , int add ) {
return ( i + l i m it +add ) % ( limit ) ;
}
/ / Function to read in data from screen
void read_input ( int & , int & , double & , double & , double&) ;
/ / Function to i n i t i a l i s e energy and magnetization
void i n i t i a l i z e ( int , double , int , double & , double&) ;
/ / The metropolis algorithm
void Metropolis ( int , long & , int , double & , double & , double ) ;
/ / p r int s to f i l e the r e s u l t s of the c alcula t io n s
void output ( int , int , double , double ) ;
int main ( int argc , char argv [ ] )
{
char outfilename ;
long idum ;
int spin_matrix , n_spins , mcs ;
double w[17 ] , average [5 ] , initial_ temp , final_temp , E , M, temp_step ;
/ / Read in output f i l e , abort i f there are too few command l ine
arguments
i f ( argc <= 1 ) {
cout < < < < argv [0] < <
< < endl ;
ex i t (1) ;
}
el se {
outfilename =argv [ 1 ] ;
}
o f i l e . open ( outfilename ) ;
/ / Read in i n i t i a l values such as s i ze of l a t t i c e , temp and
cyc les
read_input ( n_spins , mcs , initia l_te mp , final_temp , temp_step ) ;
spin_matrix = ( int ) matrix ( n_spins , n_spins , s izeof ( int ) ) ;
idum = 1; / / random s ta rt ing point
for ( double temp = in i t i al_t e m p ; temp <= final_temp ; temp+=
temp_step ) {
/ / i n i t i a l i s e energy and magnetization
E = M = 0 . ;
/ / setup array for poss ible energy changes
for ( int de = 8; de <= 8 ; de++) w[ de ] = 0 ;
for ( int de = 8; de <= 8 ; de+=4) w[ de +8] = exp( de / temp ) ;

11.2. PROGRAM EXAMPLE 197
/ / i n i t i a l i s e array for expectat ion values
for ( int i = 0 ; i < 5; i ++) average [ i ] = 0 . ;
i n i t i a l i z e ( n_spins , temp , spin_matrix , E , M) ;
/ / s t a r t Monte Carlo computation
for ( int cycles = 1 ; cycles <= mcs ; cycles ++){
Metropolis ( n_spins , idum , spin_matrix , E , M, w) ;
/ / update expectati on values
average [0 ] += E ; average [ 1 ] + = E E;
average [2 ] += M; average [3] += M M; average [ 4] + = fabs (M) ;
}
/ / p rin t r e s u l t s
output ( n_spins , mcs , temp , average ) ;
}
free_m atrix (( void ) spin_matrix ) ; / / f re e memory
o f i l e . close ( ) ; / / close output f i l e
return 0 ;
}
/ / read in input data
void read_input ( int & n_spins , int & mcs , double& in itia l_ temp ,
double& final_temp , double& temp_step )
{
cout < < ;
cin > > mcs ;
cout < < ;
cin > > n_spins ;
cout < < ;
cin > > i nit i a l_t e m p ;
cout < < ;
cin > > final_temp ;
cout < < ;
cin > > temp_step ;
} / / end of func tion read_input
/ / func tion to i n i t i a l i s e energy , spin matrix and magnetization
void i n i t i a l i z e ( int n_spins , double temp , int spin_matrix ,
double& E , double& M)
{
/ / setup spin matrix and i n t i a l magnetization
for ( int y = 0 ; y < n_spins ; y++) {
for ( int x = 0 ; x < n_spins ; x++){
spin_matrix [ y ][ x ] = 1 ; / / spin o rien t at i on for the ground s t ate
M += ( double ) spin_matrix [ y ][ x ] ;
}
}

198 CHAPTER 11. MONTE CARLO METHODS IN STATISTICAL PHYSICS
/ / setup i n i t i a l energy
for ( int y = 0 ; y < n_spins ; y++) {
for ( int x = 0 ; x < n_spins ; x++){
E = ( double ) spin_matrix [ y ][ x]
( spin_matrix [ periodic (y , n_spins , 1) ][ x ] +
spin_matrix [ y ][ periodic (x , n_spins , 1) ] ) ;
}
}
} / / end f un ctio n i n i t i a l i s e
void Metropolis ( int n_spins , long& idum , int spin_matrix , double& E
, double&M, double w)
{
/ / loop over a l l spins
for ( int y = 0 ; y < n_spins ; y++) {
for ( int x = 0 ; x < n_spins ; x++){
int ix = ( int ) ( ran1 (&idum ) ( double ) n_spins ) ;
int iy = ( int ) ( ran1 (&idum ) ( double ) n_spins ) ;
int deltaE = 2 spin_matrix [ iy ][ ix ]
( spin_matrix [ iy ][ pe ri od ic ( ix , n_spins , 1) ]+
spin_matrix [ per iodi c ( iy , n_spins , 1) ] [ ix ] +
spin_matrix [ iy ][ pe ri od ic ( ix , n_spins ,1) ] +
spin_matrix [ per iodi c ( iy , n_spins ,1) ][ ix ]) ;
i f ( ran1 (&idum ) <= w[ deltaE +8 ] ) {
spin_matrix [ iy ] [ ix ] = 1; / / f l i p one spin and accept new
spin config
M + = ( double ) 2 spin_matrix [ iy ] [ ix ] ;
E += ( double ) deltaE ;
}
}
}
} / / end of Metropolis sampling over spins
void output ( int n_spins , int mcs , double temp , double average )
{
double norm = 1 / ( ( double ) ( mcs ) ) ; / / divided by t o t a l number of
cyc les
double Eaverage = average [0] norm ;
double E2average = average [1] norm ;
double Maverage = average [2] norm ;
double M2average = average [3] norm ;
double Mabsaverage = average [4] norm ;
/ / all expect ation values are per spin , div ide by 1 / n_spins / n_spins
double Evariance = ( E2average Eaverage Eaverage ) / n_spins / n_spins ;
double Mvariance = ( M2average Mabsaverage Mabsaverage ) / n_spins /
