Hirsch M.J., Pardalos P.M., Murphey R. Dynamics of Information Systems: Theory and Applications
Подождите немного. Документ загружается.

86 T.N. Dinh et al.
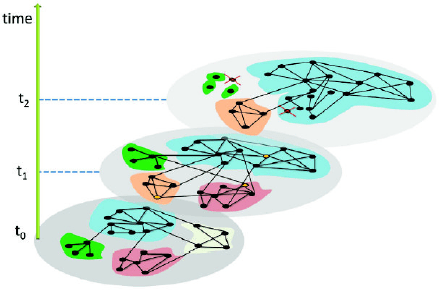
Fig. 4.1 In an evolving
network, modules can split
into smaller modules when
connectivity inside modules
weakened, or they can also
merge together to form new
modules
4.2.2 Problem Definition
We study time dependent, weighted and undirected networks. All algorithms and
definitions can also be extended naturally for directed networks. In our network
model, new nodes and links are frequently added into or removed from the network.
See Fig. 4.1 for a pictorial representation. Assume that the network is G
0
(V
0
,E
0
)
at time t
0
and it evolves into G
i
(V
i
,E
i
) at time t
i
. Denote V
i
the set of added
or removed nodes when the network evolves from G
i−1
to G
i
i.e., the symmetric
difference V
i
V
i−1
. Similarly, we denote E
i
= E
i
E
i−1
the set of added
or removed links when the network evolves from G
i−1
to G
i
. Given the network
G
i−1
(V
i−1
,E
i−1
) at time t
i−1
and the changes (V
i
,E
i
) in the network between
t
i−1
and t
i
, one can deduce G
i
(V
i
,E
i
) from the formulas V
i
= V
i−1
V
i
and
E
i
=E
i−1
E
i
.
Problem Definition Given a network and its sequences of changes over time
G
0
V
0
,E
0
,
V
1
,E
1
,...,
E
i
,E
i
,...
Devise an online algorithm to efficiently
• Detect the modules in the network at everytime point without recomputing them
from scratch, i.e., adaptively update modules overtime.
• Trace the evolution of network modules (identify the relationship between mod-
ules at different time points).
4.3 Compact Representation of a Network
Given a network G =(V , E) and its modular structure C ={C
1
,C
2
,...,C
k
}where
each disjoint subset of nodes C
i
is called a module. Our goal is to construct a new
network with equivalent structure to G but contains a significant smaller number of
nodes and links. Such a network can be used in place of G to reduce the running

4 A General Approach for Modules Identification in Evolving Networks 87
time of identifying evolving modules and many existing modules identification al-
gorithms in the current literature.
One way to construct such a compression of the network is to replace every
module by a single node with a self-loop representing the connection inside the
module [20, 21]. However, this approach might not be suitable for a general purpose
as many modules identification algorithms will not work with the presence of self-
loops.
We are inspired by an observation in biological networks that two proteins with
identical set of neighbors belong to a same functional module. Hence, instead of
introducing self-loops, we replace each module C
i
by two new nodes x
i
,y
i
that
share a same set of neighbors. The algorithm to construct the compact representa-
tion of G is presented in Algorithm 1. A link (x
i
,y
i
) with weight
Φ(C
i
)
2
is added
to represent the total weight of links inside module C
i
, lines 8 and 9. The total
weights of links crossing modules C
i
and C
j
will be distributed equally to each link
(x
i
,x
j
), (x
i
,y
j
), (y
i
,x
j
), (y
i
,y
j
), lines 13 to 18. This weight assignment will help
preserve the modular structure. If a module contains only one single node, there
will be no links inside the module. We replace that module by a single node in the
compact representation to reduce the size of the compact representation as in line 6.
From the modularity optimization viewpoint, we will prove the structure equiv-
alence of the original network and its compact representation. When we refer to the
optimal partition, we mention the partition of network into modules that maximizes
the modularity value.
Algorithm 1 Compact representation of a network
1: Input: G(V , E), partition C ={C
1
,C
2
,...,C
k
}.
2: Output: Compact representation G
(V
,E
).
3: Initialize G
(V
,E
) ←(φ, φ)
4: for each module C
i
in C do
5: if |C
i
|=1 then
6: Create a new module C
i
={x
i
} in the compact representation
7: else
8: Create a new module C
i
={x
i
,y
i
} in the compact representation
9: w(x
i
;y
i
) ←
Φ(C
i
)
2
10: end if
11: V
←V
∪C
i
12: end for
13: for all (u, v) ∈E do
14: i ←mb(u), j ←mb(v)
15: ∀(x, y) ∈C
i
×C
j
:w(x,y) ←
Φ(C
i
,C
j
)
|C
i
||C
j
|
16: end for
17: return G
(V
,E
)

88 T.N. Dinh et al.
4.3.1 Structure Preservation
Lemma 4.3.1 The contraction of G(V , E) into G
(V
,E
) preserves the modularity
i.e. Q(C
={C
1
,C
2
,...,C
k
}) =Q(C ).
Proof From the Definition (4.1):
Q(C
) =
i
Φ(C
i
)
2m
−
vol(C
i
)
2m
2
(4.2)
By the construction of G
:
Φ
C
i
=
Φ({x
i
}) =0 =Φ(C
i
) |C
i
|< 2
Φ(x
i
,y
i
) =2
Φ(C
i
)
2
=Φ(C
i
) |C
i
|≥2
(4.3)
vol
C
i
= Φ
C
i
+
j=i
Φ
C
i
,C
j
= Φ(C
i
) +
j=i
u∈C
i
,v∈C
j
w(u,v)
= Φ(C
i
) +
j=i
C
i
C
j
Φ(C
i
,C
j
)
|C
i
||C
j
|
= vol(C
i
) (4.4)
m
=
1
2
i
vol
C
i
=
1
2
i
vol(C
i
) =m (4.5)
From (4.2), (4.3), (4.4), and (4.5) it follows that Q(C
) =Q(C ).
Lemma 4.3.2 Let x
i
,y
i
∈ C
i
obtained in construction of G
(V
,E
) and C
∗
=
{C
∗
1
,C
∗
2
,...,C
∗
k
} be an arbitrary partition of G
such that x
i
,y
i
belong to different
modules in C
∗
. There exists a partition of G
with modularity higher than Q(C
∗
)
in which x
i
,y
i
belong to a same module.
Proof We show that either moving x
i
to the module contains y
i
or moving y
i
to the
module contains x
i
will result in increasing of modularity (Fig. 4.2).
We first calculate the change in modularity if we move a group of nodes S from
its module C
a
⊇S to a new module C
b
(C
a
∩C
b
=φ):
Q
S
C
a
,C
b
=
1
m
Φ(C
b
,S)−Φ(C
a
\S,S)
−
1
2m
2
vol(S)
vol(C
b
) −vol(C
a
\S)
(4.6)

4 A General Approach for Modules Identification in Evolving Networks 89
Fig. 4.2 If two nodes x
i
,y
i
are in different modules
C
x
,C
y
, we can increase the
overall modularity by either
moving x
i
to C
y
or y
i
to C
x
We will also use this formula in later proofs.
Assume that x
i
∈C
x
and y
i
∈C
y
where C
x
,C
y
∈C
∗
.
Moving x
i
from C
x
to C
y
: Using formula (4.6) with C
a
=C
x
, C
b
=C
y
, S ={x
i
}
we have:
Q
{x
i
}
C
x
,C
y
= 2
Φ({x
i
}, { y
i
})
2m
−
vol({x
i
})vol({y
i
})
4m
2
+
1
m
Φ
C
y
\{y
i
}, {x
i
}
−Φ
C
x
\{x
i
}, {x
i
}
−
1
2m
2
vol
{x
i
}
vol
C
y
\{y
i
}
−vol
C
x
\{x
i
}
(4.7)
We can similarly calculate the change in modularity moving y
i
from C
y
to C
x
.
Since x
i
and y
i
have same function in G
i.e., ∀L ⊆ V \{x
i
,y
i
}→(Φ({x
i
},L) =
Φ({y
i
},L).Wehave:
Q
{x
i
}
C
x
,C
y
+Q
{y
i
}
C
y
,C
x
=4
Φ({x
i
}, { y
i
})
2m
−
vol({x
i
})vol({y
i
})
4m
2
=
2Φ({x
i
,y
i
})
2m
−
vol
2
({x
i
,y
i
})
4m
2
=
2Φ(C
i
)
2m
−
vol
2
(C
i
)
4m
2
>
Φ(C
i
)
2m
−
vol
2
(C
i
)
4m
2
> 0 (this follows Lemma 4.3.3) (4.8)
Hence, either Q
{x
i
}
C
x
,C
y
> 0orQ
{y
i
}
C
y
,C
x
> 0.

90 T.N. Dinh et al.
The only left part is to prove that modularity of each module is nonnegative i.e.,
for a module C
i
in a network
Q(C
i
) =
Φ(C
i
)
2m
−
vol(C
i
)
2m
2
≥0 (4.9)
The equality holds only when C
i
contains only an isolated nodes or C
i
=V(G).
Lemma 4.3.3 In the optimal partition of a network G(V , E), there is no module
with a negative modularity.
Proof Assume that there exists a module C in the optimal partition C
∗
=
{C
∗
1
,C
∗
2
,...,C
∗
k
} with Q(C) < 0. Denote N ={C
| C
∈ C
∗
,Φ(C,C
)>0} the
set of modules adjacent to C. Merging C with any modules in N will not increase
the modularity. Following (4.6), we have for all C
∗
i
∈N :
Q
C
C,C
=
1
m
Φ
C
,C
−
1
2m
2
vol
C
vol(C) ≤0
Take the sum over all C
∈N , we obtain:
C
i
∈N
1
m
Φ
C
,C
−
C
i
∈N
1
2m
2
vol(C)vol(C
i
) ≤0
⇔
1
m
Φ
C
∈N
C
,C
−
1
2m
2
vol(C)vol
C
∈N
C
≤0
⇒
1
m
vol(C) −Φ(C,C)
−
1
2m
2
vol(C)vol(V \C) ≤0
⇒ 2Q(C) ≥0
We obtain a contradiction.
Theorem 4.3.1 If partition C maximizes the modularity in G(V , E), then C
=
{C
1
,C
2
,...,C
k
}obtained in the construction of compact representation G
(V
,E
)
using Algorithm 1 will be the partition with maximum modularity in G
.
Proof Let C
∗
={C
∗
1
,C
∗
2
,...,C
∗
t
}be the partition with maximum modularity in G
.
We will prove that Q(C
∗
) = Q(C
). As shown in Lemma 4.3.2,ifC
i
={x
i
,y
i
}
and x
i
∈C
∗
j
then y
i
∈C
∗
j
. Hence, we consider only partition of G
in which x
i
,y
i
are placed in a same module for all |C
i
|=2. Thus, each C
∗
j
∈ C
∗
can be decom-
posed into a union of modules in C
. There exists a partition I ={I
1
,I
2
,...,I
t
} of
{1, 2,...,k} such that C
∗
j
=
i∈I
j
C
i
, ∀j =1...t.
Construct a partition C
={C
1
,C
2
,...,C
t
} of G(V, E) corresponding to C
∗
of G
by assigning C
j
=
i∈I
j
C
i
, ∀j = 1...t. Using similar proof showed in
Lemma 4.3.1, we can prove that Q(C
) =Q(C
∗
).
4 A General Approach for Modules Identification in Evolving Networks 91
Since Q(C
) = Q(C ) ≥ Q(C
) (Lemma 4.3.1) and Q(C
) = Q(C
∗
) ≥
Q(C
).WehaveQ(C
) =Q(C
∗
).
4.3.2 Size of the Compact Representation
Worst Case Analysis In the worst case, the number of nodes in the compact rep-
resentation can reach to the number of nodes in the network. Each modules in the
network will have exactly two nodes.
Theorem 4.3.2 The size of a compact representation constructed by the Algorithm 1
is at most the size of its original network.
Proof The proof is based on the fact that each module is represented by two nodes
in the compact representation and each module in the network contains at least two
nodes.
Assume that there exists a module that contains only a single node. The modular-
ity of that module will be negative (unless the single node in the module is isolated,
but we remove isolated nodes from the network as the beginning as they have no
contribution to the modularity). We obtain the contradiction to Lemma 4.3.3.
In case the network has a module with a single node, we can always merge that
module to some neighbor module and obtain a new set of modules with higher
modularity.
In our experiments, the actual size of the compact representation is far smaller
than the theoretical bound.
Social Networks The number of nodes in the compact representation is at most
the number of modules in the network. Hence, the average number of modules is
an upper bound for the average size of the compact representation. In some social
networks [11, 12, 22], the distribution of the module size s follows the power-law
form P(s)= c · s
−α
for some constant α ≈ 2 at least for a wide range of s.Ifthe
network has n nodes, then the average number of modules
k will be
k =
n
s
=
n ×
n
s=2
c ·s
−α
n
s=2
c ·s
−α
·s
=
n ×
n
s=2
s
−α
n
s=2
s
1−α
(4.10)
where
s is the average module size of the network.
When α =2 the denominator in (4.10) can be approximated by ln n and the sum
n
s=2
c ·s
−α
in the numerator is bounded by a constant. Hence, the average size of
the compact representation is upper-bounded by O(
n
log n
).
92 T.N. Dinh et al.
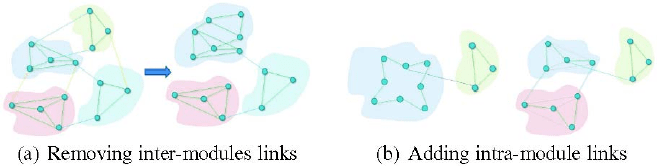
Fig. 4.3 Small changes may affect network modular structure. (a) Removing inter-modules links
usually results in more separated modules. However, in this case removing yellow inter-modules
links make modules merged. (b) Adding intra-module links usually strengthen the module. How-
ever, in this case, adding 6 white links into the light blue module make it split into two
4.4 Partition Based on Evolution History
Assume that we have a network G = (V , E) and its modular structure C =
{C
1
,C
2
,...,C
l
}. The connection inside a module is denser than connection be-
tween modules i.e., we should have more intra-module links than inter-modules
ones. Hence, intuitively adding intra-module links or removing inter-modules links
will make modules “stronger” and vice versa removing intra-module links or adding
inter-modules links will make the existing module structure less clear. In fact, re-
moving inter-modules links may cause merging of modules as shown in Fig. 4.3(a).
When two modules have less “distraction” caused by other modules, they become
more attractive to each other and can be combined as one. Other rare but pos-
sible events are splitting of the module when adding intra-links. Figure 4.3(b)
show an example in that adding 6 more white links make the module split into
two smaller ones. From the quantitative aspect, one can verify that adding an
intra-module link will not always increase the modularity of the module. Assume
that we have a module C
i
that cannot be divided further in order to increase the
modularity. Among all possible bisections of C
i
, consider {X, Y = C
i
\X} that
X, Y are the most loosely connected e.g., X, Y are obtained through the sparsest
cut in the subgraph induced by C
i
. In the case of new links crossing X and Y ,
they will enhance the local structure of C
i
. Otherwise, adding new links that
both ends belong to X or Y will make the connection inside either subcompo-
nent X or Y stronger but weaken the structure of C
i
, thus leading to the split-
ting of X and Y . Similar observations can be seen for adding and removing ver-
tices.
The behavior of splitting modules makes it extremely challenging to adaptively
update evolving modules, especially on the compact representation where each
module is represented by only two nodes. The modules splitting requires us to “un-
compact” the correcting modules. We will discuss our proposed solution in the next
section.
4 A General Approach for Modules Identification in Evolving Networks 93
4.4.1 Algorithm
The algorithm for Modules Identification in Evolving Networks (MIEN) is presented
in Algorithm 2. The presented algorithm is a general approach such that it allows the
use of any existing algorithm A on modules identification. The only requirement
for A is to work with weighted networks. This requirement is reasonable as most
existing modules identification algorithms have their weighted versions.
Assume that at time t, changes of the network are given by (V
t
,E
t
). Each
link (u, v) in E
t
will affect the weights of links crossing some modules C
i
,C
j
or
link that both ends lie in a same module C
i
in the compact representation. Updating
the weight of corresponding links in the compact representation is easy as lines 8 to
15 in Algorithm 2.
However, the compact representation of a network may not reflect evolutionary
phenomena in its original network. We note that merging of two modules C
i
and C
j
in the network G corresponds to the joining of C
i
and C
j
in the compact represen-
tation of G. However, if a module is split or some of its member are leaving to join
in other modules,running module identification algorithm A only on the compact
representation will not be able to detect those changes. Hence, when the network
evolves, we will modify the compact representation based on the changes in such a
way that the new compact representation allows the module identification algorithm
to recognize the changing in memberships.
Note that the most sensitive nodes to changing membership are newly removed
or added nodes or the ones that are incident to recently added or removed links.
For each of those nodes, say node u, we ‘exclude’ it from its compact module C
i
where i =mb(u) and assign it to a new singleton module, say C
k
. It is equivalent
to replacing the module C
i
in the compact representation by two compact modules
C
i
and C
k
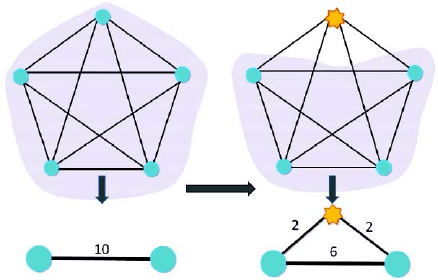
. Figure 4.4 shows an example of excluding a node from its module.
At the beginning, the module contains 5 nodes and 10 links of unit weight. The
corresponding module in the compact representation has two nodes connecting by
a link of weight 10. After the network evolves, the node marked with star has some
new incident links and is excluded from its module. The module at the beginning
now contains only 4 nodes and the link weights in the compact representation are
redistributed as shown in the figure.
The sketch of the algorithm is as follows. At the very beginning, we obtain the
modular structure of the network G(V , E) using algorithm A , lines 3 to 4. The com-
pact representation G
(V
,E
) of G is then constructed using Algorithm 1.From
now on, all operations will be performed on G
to reduce the computational cost
and time complexity.
For each time point t, we update the compact representation according to the
given change (V
t
,E
t
) as in lines 8 to 26. We handle with four separate type
of changes: set of old nodes removed (V
t−1
∩ V
t
), set of new nodes coming
(V
t
\V
t−1
), set of old links removed (E
t−1
∩ E
t
) and set of new links com-
ing (E
t
\E
t−1
).
The set of nodes that are removed at time t is given by V
t−1
∩V
t
. In lines 8
to 13, we remove those nodes from their modules. Whenever their modules contain

94 T.N. Dinh et al.
Algorithm 2 MIEN—Modules Identification in Evolving Networks
1: Input: G
0
(V
0
,E
0
), (V
1
,E
1
), . . . , (V
s
,E
s
)
2: Output: Partitions C
1
, C
2
,...,C
s
and ‘parents’ of each module.
3: Find the partition C
0
using the selected algorithm A .
4: C =C
0
←A (G
0
) ={C
1
,C
2
,...,C
l
0
}
5: G
(V
,E
) ← Compact representation of (G
0
, C
0
) using Algorithm 1.
6: for t ←1tos do
7: C
← Partition of the compact representation G
corresponding to C (as in
Algorithm 1).
8: for all u ∈V
t−1
∩V
t
do
9: Remove u from C : C
mb(u)
=C
mb(u)
−{u}
10: if |C
mb(u)
|=1 then
11: Remove y
mb(u)
from C
mb(u)
and double link weights of links coming
from x
mb(u)
12: end if
13: end for
14: for all u ∈V
t
\V
t−1
do
15: Create a new module C
t−1
mb(u)
={u} in G
16: Create a new module C
mb(u)
={x
mb(u)
} in G
17: end for
18: for all (u, v) ∈E
t
do
19:
u,v
=
+w(u,v) (u, v) ∈E
t
\E
t−1
−w(u,v) (u, v) ∈E
t−1
\E
t
20: i ←mb(u), j ←mb(v)
21: if i =j then
22: ∀(u
,v
) ∈C
i
×C
j
:w(u
,v
) =w(u
,v
) +
u,v
|C
i
||C
j
|
23: else
24: w(x
i
,y
i
) =w(x
i
,y
i
) +
u,v
25: end if
26: end for
27: Run algorithm A on the updated compact representation: C ← A (G
) =
{C
1
,C
2
,...,C
l
t
}
28: Refine the module structure C in G
following Lemmas 4.3.2, 4.3.3.
29: Reconstruct partition C ={C
t
1
,C
t
2
,...,C
t
l
t
} from C.
30: C
t
←C
31: for i ←1tol
t
do
32: parents(C
t
i
) ←{C
t−1
j
|x
j
,y
j
∈C
i
}
33: end for
34: G
(V
,E
) ← Compact representation of (G
, C)
35: end for
4 A General Approach for Modules Identification in Evolving Networks 95
Fig. 4.4 Excluding a node
from its module. Links’
weights are also updated
accordingly
only one node we simplify the corresponding module in the compact representation.
Lines 14 to 17 handle new coming nodes at time t that are given by V
t
\V
t−1
.For
each new node, we create a new module contain only that node and a corresponding
module in the compact representation. We update removing links and adding links
in lines 18 to 26 in which we distinguish two cases: links crossing two modules
(lines 21 to 22) and links resting completely in one module (lines 23 to 25).
After the changes in links and nodes are fully incorporated into the compact rep-
resentation, we run the algorithm A again on the compact representation G
(V
,E
)
to obtain the module structure in G
. To enable transforming back the modular struc-
ture in G
to the modular structure in the network G
t
(V
t
,E
t
), we refine the modular
structure C in G
following Lemma 4.3.2 i.e., if the module C
t−1
i
in V
t−1
is rep-
resented by two nodes x
i
,y
i
in the compact representation and x
i
and y
i
be placed
in different modules in G
we will move them to a same module (and increase the
modularity). We can also merge every module with negative modularity or module
with only a singleton node to one of its neighbor module to increase the modularity
as in Lemma 4.3.3 and the proof of Theorem 4.3.2.
Finally, we use the refined modular structure in G
(V
,E
) to obtain the modular
structure in G
t
(V
t
.E
t
). It can be done easily by merging modules in the network.
For example, if x
i
and x
j
are identified to be in a same module in the compact rep-
resentation, then we merge corresponding modules C
t−1
i
and C
t−1
j
in the network
together and claim that the new module is originated from C
t−1
i
and C
t−1
j
as in lines
31 to 33.
4.4.2 Complexity
Time to construct the compact representation of a network G(V , E) using Algo-
rithm 1 is O(|V |+|E|). We iterate through each link exactly once.
Time complexity of Algorithm 2 depends on the selection of the algorithm A and
the size of the compact network representation. In the compact representation, the
