Hirsch M., Smale S., Devaney R., Differential Equations, Dynamical Systems, and an Introduction to Chaos
Подождите немного. Документ загружается.

356 Chapter 15 Discrete Dynamical Systems
Prove that T is chaotic on [0, 1].
16. Consider a different “tent function” defined on all of
R by
T (x) =
3x if x ≤ 1/2
−3x + 3 if 1/2 ≤ x.
Identify the set of points whose orbits do not go to −∞. What can
you say about the dynamics of this set?
17. Use the results of the previous exercise to show that the set in
Section 15.5 is homeomorphic to the Cantor middle-thirds set.
18. Prove the following saddle-node bifurcation theorem: Suppose that f
λ
depends smoothly on the parameter λ and satisfies:
(a) f
λ
0
(x
0
) = x
0
(b) f
λ
0
(x
0
) = 1
(c) f
λ
0
(x
0
) = 0
(d)
∂f
λ
∂λ
λ=λ
0
(x
0
) = 0
Then there is an interval I about x
0
and a smooth function μ : I → R
satisfying μ(x
0
) = λ
0
and such that
f
μ(x)
(x) = x.
Moreover, μ
(x
0
) = 0 and μ
(x
0
) = 0. Hint: Apply the implicit function
theorem to G(x, λ) = f
λ
(x) − x at (x
0
, λ
0
).
19. Discuss why the saddle-node bifurcation is the “typical” bifurcation
involving only fixed points.
⫺y
*
y
*
g(⫺y
*
)
g(y
*
)
Figure 15.14 The graph of the
one-dimensional function g on
[−y
∗
, y
∗
].
Exercises 357
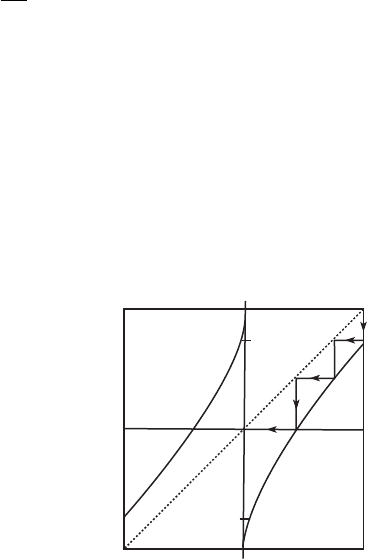
20. Recall that comprehending the behavior of the Lorenz system in
Chapter 14 could be reduced to understanding the dynamics of a certain
one-dimensional function g on an interval [−y
∗
, y
∗
] whose graph is
shown in Figure 15.14. Recall also |g
(y)| > 1 for all y = 0 and that
g is undefined at 0. Suppose now that g
3
(y
∗
) = 0 as displayed in this
graph. By symmetry, we also have g
3
(−y
∗
) = 0. Let I
0
=[−y
∗
, 0) and
I
1
= (0, y
∗
] and define the usual itinerary map on [−y
∗
, y
∗
].
(a) Describe the set of possible itineraries under g .
(b) What are the possible periodic points for g ?
(c) Prove that g is chaotic on [−y
∗
, y
∗
].
This Page Intentionally Left Blank

16
Homoclinic Phenomena
In this chapter we investigate several other three-dimensional systems of dif-
ferential equations that display chaotic behavior. These systems include the
Shil’nikov system and the double scroll attractor. As with the Lorenz system,
our principal means of studying these systems involves reducing them to lower
dimensional discrete dynamical systems, and then invoking symbolic dynam-
ics. In these cases the discrete system is a planar map called the horseshoe map.
This was one of the first chaotic systems to be analyzed completely.
16.1 The Shil’nikov System
In this section we investigate the behavior of a nonlinear system of differential
equations that possesses a homoclinic solution to an equilibrium point that is
a spiral saddle. While we deal primarily with a model system here, the work of
Shil’nikov and others [4, 40, 41], shows that the phenomena described in this
chapter hold in many actual systems of differential equations. Indeed, in the
exploration at the end of this chapter, we investigate the system of differential
equations governing the Chua circuit, which, for certain parameter values, has
a pair of such homoclinic solutions.
For this example, we do not specify the full system of differential equations.
Rather, we first set up a linear system of differential equations in a certain cylin-
drical neighborhood of the origin. This system has a two-dimensional stable
surface in which solutions spiral toward the origin and a one-dimensional
unstable curve. We then make the simple but crucial dynamical assumption
that one of the two branches of the unstable curve is a homoclinic solution
359
360 Chapter 16 Homoclinic Phenomena
and thus eventually enters the stable surface. We do not write down a specific
differential equation having this behavior. Although it is possible to do so,
having the equations is not particularly useful for understanding the global
dynamics of the system. In fact, the phenomena we study here depend only
on the qualitative properties of the linear system described previously a key
inequality involving the eigenvalues of this linear system, and the homoclinic
assumption.
The first portion of the system is defined in the cylindrical region
S of R
3
given by x
2
+ y
2
≤ 1 and |z|≤1. In this region consider the linear system
X
=
⎛
⎝
−110
−1 −10
002
⎞
⎠
X.
The associated eigenvalues are −1 ± i and 2. Using the results of Chapter 6,
the flow φ
t
of this system is easily derived:
x(t ) = x
0
e
−t
cos t + y
0
e
−t
sin t
y(t) =−x
0
e
−t
sin t + y
0
e
−t
cos t
z(t ) = z
0
e
2t
.
Using polar coordinates in the xy–plane, solutions in
S are given more
succinctly by
r(t ) = r
0
e
−t
θ(t ) = θ
0
− t
z(t ) = z
0
e
2t
.
This system has a two-dimensional stable plane (the xy–plane) and a pair of
unstable curves ζ
±
lying on the positive and negative z-axis, respectively.
We remark that there is nothing special about our choice of eigenvalues for
this system. Everything below works fine for eigenvalues α ± iβ and λ where
α < 0, β = 0, and λ > 0 subject only to the important condition that λ > −α.
The boundary of
S consists of three pieces: the upper and lower disks
D
±
given by z =±1, r ≤ 1, and the cylindrical boundary C given by
r = 1, |z|≤1. The stable plane meets C along the circle z = 0 and divides
C into two pieces, the upper and lower halves given by C
+
and C
−
, on which
z>0 and z<0, respectively. We may parametrize D
±
by r and θ and C by θ
and z. We will concentrate in this section on C
+
.
Any solution of this system that starts in C
+
must eventually exit from S
through D
+
. Hence we can define a map ψ
1
: C
+
→ D
+
given by following
solution curves that start in C
+
until they first meet D
+
. Given (θ
0
, z
0
) ∈ C
+
,

16.1 The Shil’nikov System 361
let τ = τ (θ
0
, z
0
) denote the time it takes for the solution through (θ
0
, z
0
)to
make the transit to D
+
. We compute immediately using z(t ) = z
0
e
2t
that
τ =−log(
√
z
0
). Therefore
ψ
1
⎛
⎝
1
θ
0
z
0
⎞
⎠
=
⎛
⎝
r
1
θ
1
1
⎞
⎠
=
⎛
⎝
√
z
0
θ
0
+ log
√
z
0
1
⎞
⎠
.
For simplicity, we will regard ψ
1
as a map from the (θ
0
, z
0
) cylinder to the
(r
1
, θ
1
) plane. Note that a vertical line given by θ
0
= θ
∗
in C
+
is mapped by
ψ
1
to the spiral
z
0
→
√
z
0
, θ
∗
+ log
√
z
0
,
which spirals down to the point r = 0inD
±
, since log
√
z
0
→−∞as z
0
→ 0.
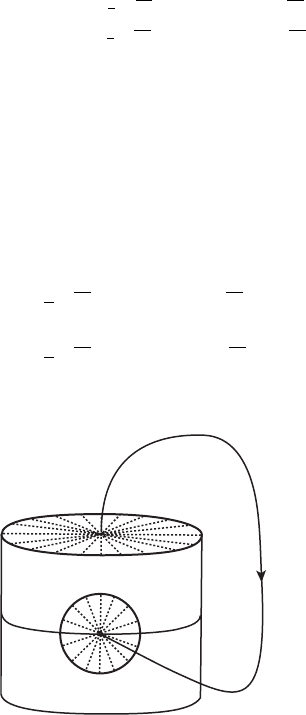
To define the second piece of the system, we assume that the branch ζ
+
of the unstable curve leaving the origin through D
+
is a homoclinic solution.
That is, ζ
+
eventually returns to the stable plane. See Figure 16.1. We assume
that ζ
+
first meets the cylinder C at the point r = 1, θ = 0, z = 0. More
precisely, we assume that there is a time t
1
such that φ
t
1
(0, θ ,1) = (1, 0, 0) in
r, θ , z coordinates.
Therefore we may define a second map ψ
2
by following solutions beginning
near r = 0inD
+
until they reach C. We will assume that ψ
2
is, in fact,
defined on all of D
+
. In Cartesian coordinates on D
+
, we assume that ψ
2
takes (x, y) ∈ D
+
to (θ
1
, z
1
) ∈ C via the rule
ψ
2
x
y
=
θ
1
z
1
=
y/2
x/2
.
f
⫹
Figure 16.1 The homoclinic orbit ζ
+
.
362 Chapter 16 Homoclinic Phenomena
In polar coordinates, ψ
2
is given by
θ
1
= (r sin θ)/2
z
1
= (r cos θ)/2.
Of course, this is a major assumption, since writing down such a map for a
particular nonlinear system would be virtually impossible.
Now the composition = ψ
2
◦ ψ
1
defines a Poincaré map on C
+
. The
map ψ
1
is defined on C
+
and takes values in D
+
, and then ψ
2
takes values in
C. We have : C
+
→ C where
θ
0
z
0
=
θ
1
z
1
=
1
2
√
z
0
sin
θ
0
+ log(
√
z
0
)
1
2
√
z
0
cos
θ
0
+ log(
√
z
0
)
.
See Figure 16.2.
As in the Lorenz system, we have now reduced the study of the flow of this
three-dimensional system to the study of a planar discrete dynamical system.
As we shall see in the next section, this type of mapping has incredibly rich
dynamics that may be (partially) analyzed using symbolic dynamics. For a little
taste of what is to come, we content ourselves here with just finding the fixed
points of . To do this we need to solve
θ
0
=
1
2
√
z
0
sin
θ
0
+ log(
√
z
0
)
z
0
=
1
2
√
z
0
cos
θ
0
+ log(
√
z
0
)
.
v
2
(D
⫹
)
f
⫹
D
⫹
C
⫹
C
⫺
Figure 16.2 The map ψ
2
:
D
+
→ C.

16.1 The Shil’nikov System 363
These equations look pretty formidable. However, if we square both equations
and add them, we find
θ
2
0
+ z
2
0
=
z
0
4
so that
θ
0
=±
1
2
z
0
− 4z
2
0
,
which is well defined provided that 0 ≤ z
0
≤ 1/4. Substituting this expression
into the second equation above, we find that we need to solve
cos
±
1
2
z
0
− 4z
2
0
+ log
√
z
0
= 2
√
z
0
.
Now the term
z
0
− 4z
2
0
tends to zero as z
0
→ 0, but log(
√
z
0
) →−∞.
Therefore the graph of the left-hand side of this equation oscillates infinitely
many times between ±1asz
0
→ 0. Hence there must be infinitely many
places where this graph meets that of 2
√
z
0
, and so there are infinitely many
solutions of this equation. This, in turn, yields infinitely many fixed points for
. Each of these fixed points then corresponds to a periodic solution of the
system that starts in C
+
, winds a number of times around the z-axis near the
origin, and then travels around close to the homoclinic orbit until closing up
when it returns to C
+
. See Figure 16.3.
f
⫹
c
Figure 16.3 A periodic solution γ
near the homoclinic solution ζ
+
.
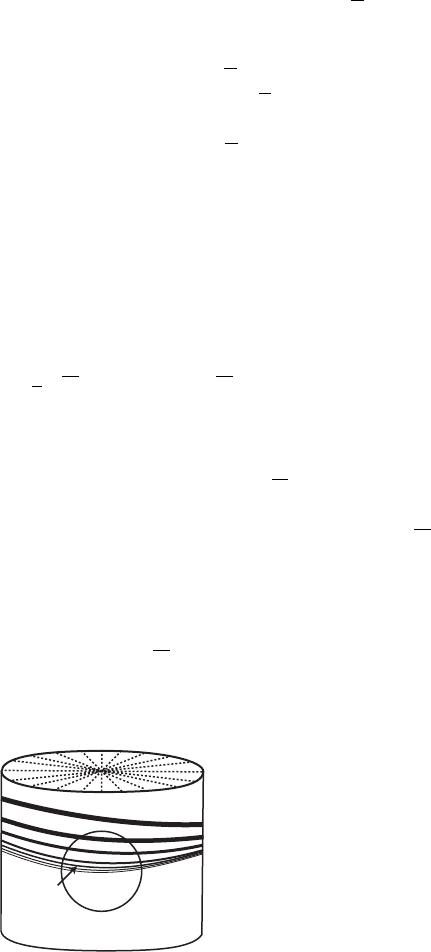
364 Chapter 16 Homoclinic Phenomena
We now describe the geometry of this map; in the next section we use these
ideas to investigate the dynamics of a simplified version of this map. First note
that the circles z
0
= α in C
+
are mapped by ψ
1
to circles r =
√
α centered at
r = 0inD
+
since
ψ
1
θ
0
α
=
r
1
θ
1
=
√
α
θ
0
+ log(
√
α)
.
Then ψ
2
maps these circles to circles of radius
√
α/2 centered at θ
1
= z
1
= 0
in C. (To be precise, these are circles in the θz–plane; in the cylinder, these
circles are “bent.”) In particular, we see that “one-half” of the domain C
+
is
mapped into the lower part of the cylinder C
−
and therefore no longer comes
into play.
Let H denote the half-disk (C
+
) ∩{z ≥ 0}. Half-disk H has center at
θ
1
= z
1
= 0 and radius 1/2. The preimage of H in C
+
consists of all points
(θ
0
, z
0
) whose images satisfy z
1
≥ 0, so that we must have
z
1
=
1
2
√
z
0
cos
θ
0
+ log(
√
z
0
)
≥ 0.
It follows that the preimage of H is given by
−1
(H) ={(θ
0
, z
0
) |−π /2 ≤ θ
0
+ log(
√
z
0
) ≤ π /2}
where 0 <z
0
≤ 1. This is a region bounded by the two curves θ
0
+log(
√
z
0
) =
±π/2, each of which spirals downward in C
+
toward the circle z = 0.
See Figure 16.4. This follows since, as z
0
→ 0, we must have θ
0
→∞.
More generally, consider the curves
α
given by
θ
0
+ log(
√
z
0
) = α
D
⫹
C
⫹
C
⫺
H
Φ
⫺1
(H)
Figure 16.4 The half-disk H and
its preimage in C
+
.
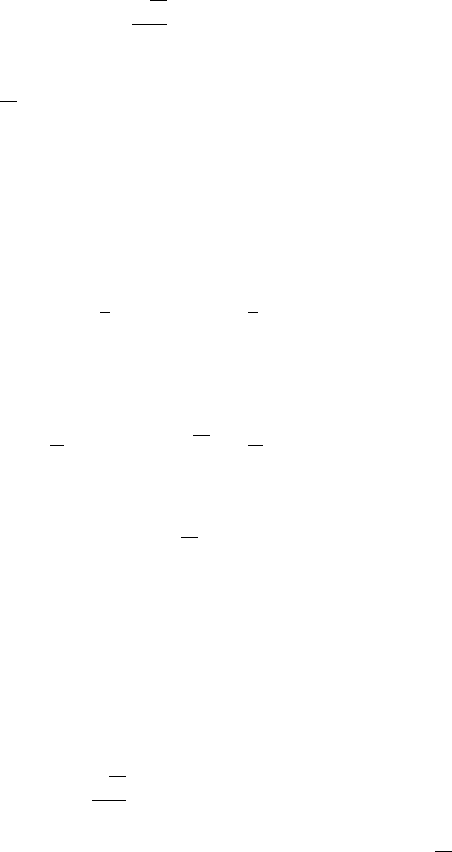
16.1 The Shil’nikov System 365
for −π /2 ≤ α ≤ π/2. These curves fill the preimage
−1
(H) and each spirals
around C just as the boundary curves do. Now we have
(
α
) =
√
z
0
2
sin α
cos α
,
so maps each
α
to a ray that emanates from θ = z = 0inC
+
and is
parameterized by
√
z
0
. In particular, maps each of the boundary curves
±π/2
to z = 0inC.
Since the curves
±π/2
spiral down toward the circle z = 0inC, it follows
that
−1
(H) meets H in infinitely many strips, which are nearly horizontal
close to z = 0. See Figure 16.4. We denote these strips by H
k
for k sufficiently
large. More precisely, let H
k
denote the component of
−1
(H) ∩H for which
we have
2kπ −
1
2
≤ θ
0
≤ 2kπ +
1
2
.
The top boundary of H
k
is given by a portion of the spiral
π/2
and the bottom
boundary by a piece of
−π/2
. Using the fact that
−
π
2
≤ θ
0
+ log
√
z
0
≤
π
2
,
we find that, if (θ
0
, z
0
) ∈ H
k
, then
−(4k + 1)π − 1 ≤−π − 2θ
0
≤ 2 log
√
z
0
≤ π − 2θ
0
≤−(4k − 1)π + 1
from which we conclude that
exp(−(4k + 1)π − 1) ≤ z
0
≤ exp(−(4k − 1)π + 1).
Now consider the image of H
k
under . The upper and lower boundaries
of H
k
are mapped to z = 0. The curves
α
∩ H
k
are mapped to arcs in rays
emanating from θ = z = 0. These rays are given as above by
√
z
0
2
sin α
cos α
.
In particular, the curve
0
is mapped to the vertical line θ
1
= 0, z
1
=
√
z
0
/2.
Using the above estimate of the size of z
0
in H
k
, one checks easily that the image
of
0
lies completely above H
k
when k ≥ 2. Therefore the image of (H
k
)isa
“horseshoe-shaped” region that crosses H
k
twice as shown in Figure 16.5. In
particular, if k is large, the curves
α
∩H
k
meet the horsehoe (H
k
) in nearly
horizontal subarcs.
