Hirsch M., Smale S., Devaney R., Differential Equations, Dynamical Systems, and an Introduction to Chaos

Подождите немного. Документ загружается.

366 Chapter 16 Homoclinic Phenomena

Φ(H

)

Figure 16.5 The image of H

is a

horseshoe that crosses H

twice

in C

Such a map is called a horseshoe map; in the next section we discuss the

prototype of such a function.

16.2 The Horseshoe Map

Symbolic dynamics, which played such a crucial role in our understanding of

the one-dimensional logistic map, can also be used to study higher dimensional

phenomena. In this section, we describe an important example in

, the

horseshoe map [43]. We shall see that this map has much in common with the

Poincaré map described in the previous section.

To deﬁne the horseshoe map, we consider a region D consisting of three

components: a central square S with sides of length 1, together with two

semicircles D

and D

at the top and bottom. D is shaped like a “stadium.”

The horseshoe map F takes D inside itself according to the following pre-

scription. First, F linearly contracts S in the horizontal direction by a factor

δ < 1/2 and expands it in the vertical direction by a factor of 1/δ so that S is

long and thin, and then F curls S back inside D in a horseshoe-shaped ﬁgure

as displayed in Figure 16.6. We stipulate that F maps S linearly onto the two

vertical “legs”of the horseshoe.

We assume that the semicircular regions D

and D

are mapped inside D

as depicted. We also assume that there is a ﬁxed point in D

that attracts all

other orbits in D

. Note that F(D) ⊂ D and that F is one-to-one. However,

since F is not onto, the inverse of F is not globally deﬁned. The remainder of

this section is devoted to the study of the dynamics of F in D.

Note ﬁrst that the preimage of S consists of two horizontal rectangles, H

and H

, which are mapped linearly onto the two vertical components V

and

of F(S) ∩ S. The width of V

and V

is therefore δ, as is the height of H

and H

. See Figure 16.7. By linearity of F : H

→ V

and F : H

→ V

,we

know that F takes horizontal and vertical lines in H

to horizontal and vertical

lines in V

for j = 1, 2. As a consequence, if both h and F(h) are horizontal

line segments in S, then the length of F(h)isδ times the length of h. Similarly,

16.2 The Horseshoe Map 367

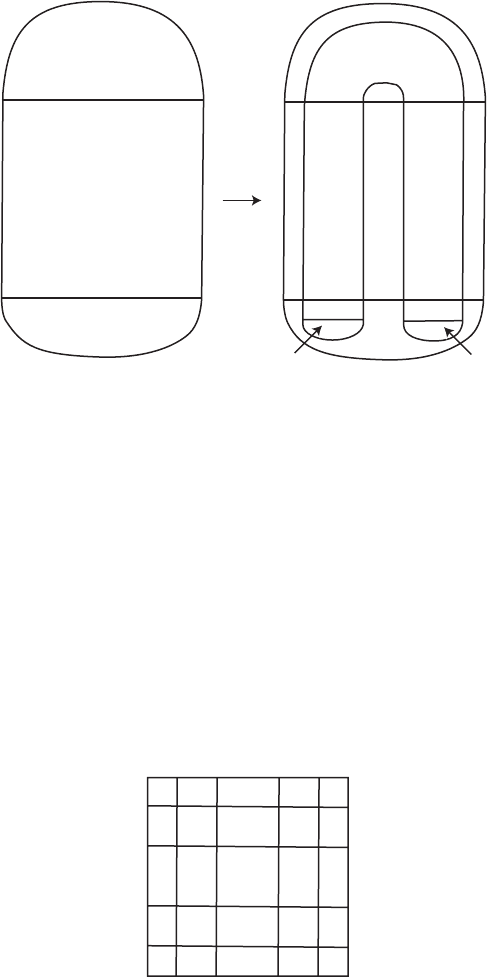
F(D

)

F(D

)

F(S)

Figure 16.6 The first iterate of the horseshoe map.

if v is a vertical line segment in S whose image also lies in S, then the length of

F(v)is1/δ times the length of v.

We now describe the forward orbit of each point X ∈ D. Recall that the

forward orbit of X is given by {F

(X) |n ≥ 0}. By assumption, F has a unique

ﬁxed point X

in D

and lim

n→∞

(X) = X

for all X ∈ D

. Also, since

F(D

) ⊂ D

, all forward orbits in D

behave likewise. Similarly, if X ∈ S but

(X) ∈ S for some k>0, then we must have that F

(X) ∈ D

∪ D

so that

(X) → X

as n →∞as well. Consequently, we understand the forward

orbits of any X ∈ D whose orbit enters D

, so it sufﬁces to consider the set of

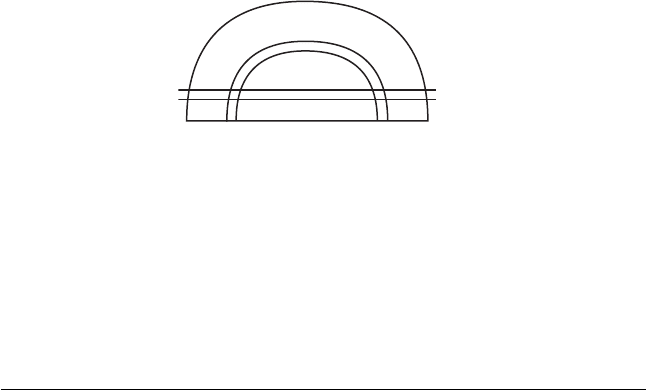
Figure 16.7 The

rectangles H

and H

and

their images V

and V

368 Chapter 16 Homoclinic Phenomena

points whose forward orbits never enter D

and so lie completely in S. Let



={X ∈ S |F

(X) ∈ S for n = 0, 1, 2, ...}.

We claim that 

has properties similar to the corresponding set for the

one-dimensional logistic map described in Chapter 15.

If X ∈ 

, then F (X) ∈ S, so we must have that either X ∈ H

or X ∈ H

for all other points in S are mapped into D

or D

. Since F

(X) ∈ S as well,

we must also have F(X ) ∈ H

∪H

, so that X ∈ F

−1

∪H

). Here F

−1

(W )

denotes the preimage of a set W lying in D. In general, since F

(X) ∈ S,we

have X ∈ F

−n

∪ H

). Thus we may write



∞



n=0

−n

∪ H

Now if H is any horizontal strip connecting the left and right boundaries of

S with height h, then F

−1

(H) consists of a pair of narrower horizontal strips

of height δh, one in each of H

and H

. The images under F of these narrower

strips are given by H ∩ V

and H ∩ V

. In particular, if H = H

, F

−1

)isa

pair of horizontal strips, each of height δ

, with one in H

and the other in H

Similarly, F

−1

)) = F

−2

) consists of four horizontal strips, each of

height δ

, and F

−n

) consists of 2

horizontal strips of width δ

n+1

. Hence

the same procedure we used in Section 15.5 shows that 

is a Cantor set of

line segments, each extending horizontally across S.

The main difference between the horseshoe and the logistic map is that, in

the horseshoe case, there is a single backward orbit rather than inﬁnitely many

such orbits. The backward orbit of X ∈ S is {F

−n

(X) |n = 1, 2, ...}, provided

−n

(X) is deﬁned and in D.IfF

−n

(X) is not deﬁned, then the backward

orbit of X terminates. Let 

−

denote the set of points whose backward orbit

is deﬁned for all n and lies entirely in S.IfX ∈ 

−

, then we have F

−n

(X) ∈ S

for all n ≥ 1, which implies that X ∈ F

(S) for all n ≥ 1. As above, this forces

X ∈ F

∪ H

) for all n ≥ 1. Therefore we may also write



−

∞



n=1

∪ H

On the other hand, if X ∈ S and F

−1

(X) ∈ S, then we must have X ∈

F(S) ∩ S, so that X ∈ V

or X ∈ V

. Similarly, if F

−2

(X) ∈ S as well, then

X ∈ F

(S) ∩ S, which consists of four narrower vertical strips, two in V

and

two in V

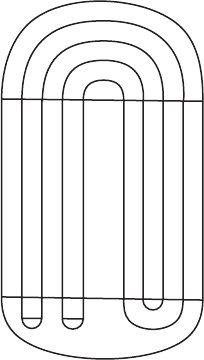
. In Figure 16.8 we show the image of D under F

. Arguing entirely

analogously as above, it is easy to check that 

−

consists of a Cantor set of

vertical lines.

16.2 The Horseshoe Map 369

Figure 16.8 The

second iterate of the

horseshoe map.

Let

 = 

∩ 

−

be the intersection of these two sets. Any point in  has its entire orbit (both

the backward and forward orbit) in S.

To introduce symbolic dynamics into this picture, we will assign a doubly

inﬁnite sequence of 0’s and 1’s to each point in .IfX ∈ , then, from the

above, we have

X ∈

∞



n=−∞

∪ H

Thus we associate to X the itinerary

S(X) = (...s

−2

−1

· s

...)

where s

= 0or1ands

= k if and only if F

(X) ∈ H

. This then provides us

with the symbolic dynamics on . Let 

denote the set of all doubly inﬁnite

sequences of 0’s and 1’s:



={(s) = (...s

−2

−1

· s

...) |s

= 0or1}.

370 Chapter 16 Homoclinic Phenomena

We impose a distance function on 

by deﬁning

d((s), (t)) =

∞



i=−∞

− t

|i|

as in Section 15.5. Thus two sequences in 

are “close” if they agree in all k

spots where |k|≤n for some (large) n. Deﬁne the (two-sided) shift map σ by

σ (...s

−2

−1

· s

...) = (...s

−2

−1

· s

...).

That is, σ simply shifts each sequence in 

one unit to the left (equivalently,

σ shifts the decimal point one unit to the right). Unlike our previous (one-

sided) shift map, this map has an inverse. Clearly, shifting one unit to the right

gives this inverse. It is easy to check that σ is a homeomorphism on 

(see

Exercise 2 at the end of this chapter).

The shift map is now the model for the restriction of F to . Indeed, the

itinerary map S gives a conjugacy between F on  and σ on 

. For if X ∈ 

and S(X ) = (...s

−2

−1

· s

...), then we have X ∈ H

, F(X ) ∈ H

−1

(X) ∈ H

−1

, and so forth. But then we have F(X ) ∈ H

, F(F(X )) ∈ H

X = F

−1

(F(X )) ∈ H

, and so forth. This tells us that the itinerary of F(X )is

(...s

−1

· s

...), so that

S(F(x)) = (...s

−1

· s

...) = σ (S(X )),

which is the conjugacy equation. We leave the proof of the fact that S is a

homeomorphism to the reader (see Exercise 3).

All of the properties that held for the old one-sided shift from the previous

chapter hold for the two-sided shift σ as well. For example, there are precisely

periodic points of period n for σ and there is a dense orbit for σ . Moreover, F

is chaotic on  (see Exercises 4 and 5). But new phenomena are present as well.

We say that two points X

and X

are forward asymptotic if F

), F

) ∈ D

for all n ≥ 0 and

lim

n→∞



) − F

)



= 0.

Points X

and X

are backward asymptotic if their backward orbits are deﬁned

for all n and the above limit is zero as n →−∞. Intuitively, two points in D

are forward asymptotic if their orbits approach each other as n →∞. Note

that any point that leaves S under forward iteration of F is forward asymptotic

to the ﬁxed point X

∈ D

. Also, if X

and X

lie on the same horizontal line

in 

, then X

and X

are forward asymptotic. If X

and X

lie on the same

vertical line in 

−

, then they are backward asymptotic.

16.2 The Horseshoe Map 371

We deﬁne the stable set of X to be

(X) =



Z || F

(Z) − F

(X)|→0asn →∞



The unstable set of X is given by

(X) =



Z || F

−n

(X) − F

−n

(Z)|→0asn →∞



Equivalently, a point Z lies in W

(X)ifX and Z are forward asymptotic.

As above, any point in S whose orbit leaves S under forward iteration of the

horseshoe map lies in the stable set of the ﬁxed point in D

The stable and unstable sets of points in  are more complicated. For

example, consider the ﬁxed point X

∗

, which lies in H

and therefore has the

itinerary (...00 · 000 ...). Any point that lies on the horizontal segment 

through X

∗

lies in W

∗

). But there are many other points in this stable set.

Suppose the point Y eventually maps into 

. Then there is an integer n such

that |F

(Y ) − X

∗

| < 1. Hence

n+k

(Y ) − X

∗

| < δ

and it follows that Y ∈ W

∗

). Thus the union of horizontal intervals given

by F

−k

(

) for k = 1, 2, 3, ...all lie in W

∗

). The reader may easily check

that there are 2

such intervals.

Since F (D) ⊂ D, the unstable set of the ﬁxed point X

∗

assumes a somewhat

different form. The vertical line segment 

through X

∗

in D clearly lies in

∗

). As above, all of the forward images of 

also lie in D. One may

easily check that F

(

) is a “snake-like” curve in D that cuts vertically across

S exactly 2

times. See Figure 16.9. The union of these forward images is then

a very complicated curve that passes through S inﬁnitely often. The closure of

this curve in fact contains all points in  as well as all of their unstable curves

(see Exercise 12).

The stable and unstable sets in  are easy to describe on the shift level. Let

∗

= (...s

∗

−2

∗

−1

· s

∗

...) ∈ 

Clearly, if t is a sequence whose entries agree with those of s

∗

to the right of

some entry, then t ∈ W

∗

). The converse of this is also true, as is shown in

Exercise 6.

A natural question that arises is the relationship between the set  for the

one-dimensional logistic map and the corresponding  for the horseshoe map.

Intuitively, it may appear that the  for the horseshoe has many more points.

However, both ’s are actually homeomorphic! This is best seen on the shift

level.

372 Chapter 16 Homoclinic Phenomena

Figure 16.9 The unstable

set for X

∗

in D.

Let 

denote the set of one-sided sequences of 0’s and 1’s and 

the set

of two-sided such sequences. Deﬁne a map

 : 

→ 

(s

...) = (...s

· s

...).

It is easy to check that  is a homeomorphism between 

and 

(see Exercise 11).

Finally, to return to the subject of Section 16.1, note that the return map

investigated in that section consists of inﬁnitely many pieces that resemble

the horseshoe map of this section. Of course, the horseshoe map here was

effectively linear in the region where the map was chaotic, so the results in

this section do not go over immediately to prove that the return maps near

the homoclinic orbit have similar properties. This can be done; however, the

techniques for doing so (involving a generalized notion of hyperbolicity) are

beyond the scope of this book. See [13] or [36] for details.

16.3 The Double Scroll Attractor

In this section we continue the study of behavior near homoclinic solutions in

a three-dimensional system. We return to the system described in Section 16.1,

16.3 The Double Scroll Attractor 373

⫹

⫺

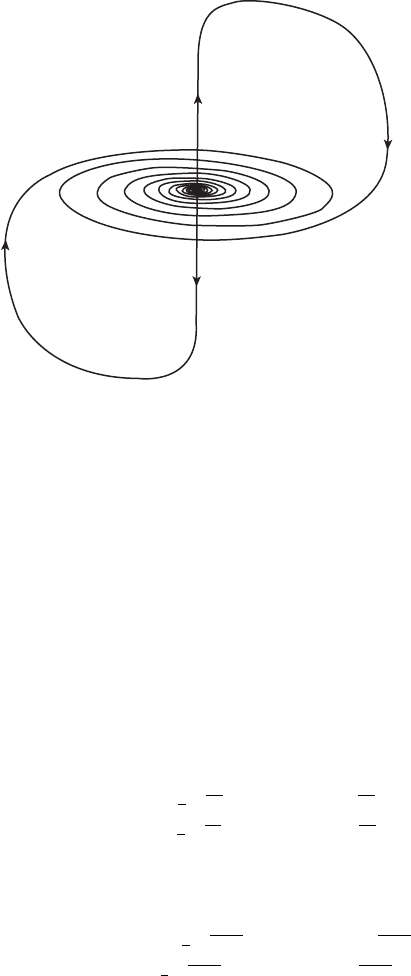
Figure 16.10 The homoclinic orbits ζ

only now we assume that the vector ﬁeld is skew-symmetric about the origin. In

particular, this means that both branches of the unstable curve at the orgin, ζ

now yield homoclinic solutions as depicted in Figure 16.10. We assume that

meets the cylinder C given by r = 1, |z|≤1 at the point θ = 0, z = 0,

so that ζ

−

meets the cylinder at the diametrically opposite point, θ = π ,

z = 0.

As in the Section 16.1, we have a Poincaré map  deﬁned on the cylinder C.

This time, however, we cannot disregard solutions that reach C in the region

z<0; now these solutions follow the second homoclinic solution ζ

−

around

until they reintersect C. Thus  is deﬁned on all of C −{z = 0}.

As before, the Poincaré map 

deﬁned in the top half of the cylinder, C

is given by













√

sin



+ log(

√

)



√

cos



+ log(

√

)





Invoking the symmetry, a computation shows that 

−

on C

−

is given by



−











π −

√

−z

sin



+ log(

√

−z

)



√

−z

cos



+ log(

√

−z

)





where z

< 0 and θ

is arbitrary. Hence (C

) is the disk of radius 1/2 centered

at θ = 0, z = 0, while (C

−

) is a similar disk centered at θ = π, z = 0.

374 Chapter 16 Homoclinic Phenomena

⫺

⫹

⌽(C

⫺

)⌽(C

⫹

)

⫺1

Figure 16.11 (C

) ∩ C, where we

have displayed the cylinder C as a

strip.

The centers of these disks do not lie in the image, because these are the points

where ζ

enters C. See Figure 16.11.

Now let X ∈ C. Either the solution through X lies on the stable surface of

the origin, or else (X) is deﬁned, so that the solution through X returns to C

at some later time. As a consequence, each point X ∈ C has the property that

1. Either the solution through X crosses C inﬁnitely many times as t →∞,

so that 

(X) is deﬁned for all n ≥ 0, or

2. The solution through X eventually meets z = 0 and hence lies on the

stable surface through the origin.

In backward time, the situation is different: only those points that lie in (C

)

have solutions that return to C; strictly speaking, we have not deﬁned the

backward solution of points in C −(C

), but we think of these solutions as

being deﬁned in

and eventually meeting C, after which time these solutions

continually revisit C.

As in the case of the Lorenz attractor, we let

A =

∞



n=0



(C)

where



(C). Then we set

A =





t∈R

(A)





{(0, 0, 0)}.

Note that



(C)−

solutions ζ

with C. Therefore we only need to add the origin to A to ensure

that

A is a closed set.

16.4 Homoclinic Bifurcations 375

The proof of the following result is similar in spirit to the corresponding

result for the Lorenz attractor in Section 14.4.

Proposition. The set

A has the following properties:

A is compact and invariant;

2. There is an open set U containing

A such that for each X ∈ U,φ

(X) ∈ U

for all t ≥ 0 and ∩

t≥0

(U ) = A.



Thus A has all of the properties of an attractor except the transitivity property.

Nonetheless,

A is traditionally called a double scroll attractor.

We cannot compute the divergence of the double scroll vector ﬁeld as we

did in the Lorenz case for the simple reason that we have not written down the

formula for this system. However, we do have an expression for the Poincaré

map . A straightforward computation shows that det D = 1/8. That is,

the Poincaré map  shrinks areas by a factor of 1/8 at each iteration. Hence

A =∩

n≥0



Proposition. The volume of the double scroll attractor

A is zero. 

16.4 Homoclinic Bifurcations

In higher dimensions, bifurcations associated with homoclinic orbits may lead

to horribly (or wonderfully, depending on your point of view) complicated

behavior. In this section we give a brief indication of some of the ramiﬁcations

of this type of bifurcation. We deal here with a speciﬁc perturbation of the

double scroll vector ﬁeld that breaks both of the homoclinic connections.

The full picture of this bifurcation involves understanding the “unfolding”

of inﬁnitely many horseshoe maps. By this we mean the following. Consider

a family of maps F

deﬁned on a rectangle R with parameter λ ∈[0, 1]. The

image of F

(R) is a horseshoe as displayed in Figure 16.12. When λ = 0,

(R) lies below R.Asλ increases, F

(R) rises monotonically. When λ = 1,

(R) crosses R twice and we assume that F

is the horseshoe map described

in Section 16.2.

Clearly, F

has no periodic points whatsoever in R, but by the time λ has

reached 1, inﬁnitely many periodic points have been born, and other chaotic

behavior has appeared. The family F

has undergone inﬁnitely many bifur-

cations en route to the horseshoe map. How these bifurcations occur is the

subject of much contemporary research in mathematics.

The situation here is signiﬁcantly more complex than the bifurcations that

occur for the one-dimensional logistic family f

(x) = λx(1 −x) with 0 ≤ λ ≤

4. The bifurcation structure of the logistic family has recently been completely

determined; the planar case is far from being resolved.