Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

560 Hermann Weing¨artner

1.75

1.25

1.50

0 0.2

0.4

0.6

0.8

10 D/m s

2 1

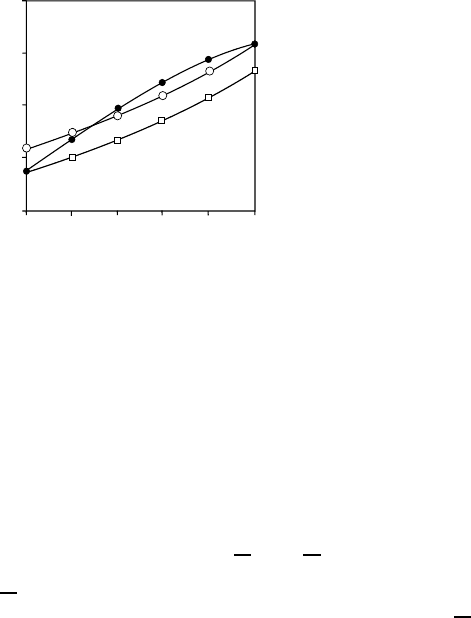
Fig. 14.1. Composition dependence of diﬀusion coeﬃcients in the system mesithy-

lene (1) + carbon tetrachloride (2) at 298.15 K: D

(open circles), D

(squares),

(ﬁlled circles).

frame of choice for ternary and multi-component systems in the presence of a

large excess of one of the components. Moreover, when describing diﬀusion in

electrolyte solutions, it is also quite natural to express mass ﬂows in aqueous

electrolyte solutions relative to the solvent water at rest (see Chap. 17).

Presuming that experimental ﬂuxes are indeed measured in the volume-

ﬁxed frame, one can show that the two mass ﬂows are not independent. The

special choice of the coordinate system imposes the condition [1]

+ J

=0. (14.5)

The

are the partial speciﬁc volumes of the components a =1, 2. Using the

thermodynamic deﬁnition of the partial speciﬁc volumes,

=(∂V/∂m

)

p,T

where m

is the mass of component a in the total volume V ,andtheir

interconnection via the Gibbs-Duhem equation, one can rigorously show that

= D

. (14.6)

Thus, the mutual-diﬀusion coeﬃcient is one and the same value, regardless

of which of the components is monitored in the diﬀusion experiment.

Fig. 14.1 shows as an example the composition dependence of the mutual-

diﬀusion coeﬃcient in the system mesithylene + carbon tetrachloride, which

is a standard example for systems with speciﬁc interactions between dislike

components [26]. This interaction between mesithylene and carbon tetrachlo-

ride is well established from thermodynamic data. The ﬁgure also contains

the self-diﬀusion coeﬃcients of both components. It is seen that the concen-

tration dependence of D

diﬀers markedly in shape from those of D

and D

It is also not correlated with the concentration dependence of other transport

coeﬃcients such as the viscosity.

One may however note that at both ends of the concentration range self-

and mutual-diﬀusion coeﬃcients approach one another. In fact, at trace con-

centration of a component the self-diﬀusion coeﬃcient of this component

14 Mutual Diﬀusion in Mixtures 561

approaches the mutual-diﬀusion coeﬃcient. This limiting behavior evolves

from rigorous theory, and is well established experimentally.

One attempt to bring some order into this confusing behavior is related

to a more detailed analysis of the driving force of diﬀusion. From the point of

view of thermodynamics, as described later in Sect. 14.4, the correct driving

force of diﬀusion is the gradient of the chemical potential rather than the

concentration gradient. Noting that

grad c



∂c

∂µ



grad µ

, (14.7)

and rewriting the concentration in terms of mole fractions leads to a trans-

formation factor of the form

Q =

dlna

dlnx

dlna

dlnx

, (14.8)

where a

is the activity of component i. Q is denoted as thermodynamic

factor. Therefore, one often considers the experimental diﬀusion coeﬃcient

to consist of a product of a thermodynamic diﬀusion coeﬃcient D

∗

which refers to the correct driving force and the correction term Q, i.e.

= D

∗

Q. (14.9)

From this line of arguing it is more convenient to compare and interpret data

for the quotient D

/Q rather than D

itself . In practice, the concentration

dependence of Q is often stronger than that of D

∗

, and the superposition

of the two terms often leads to quite complex concentration dependencies

of D

[1]. It is shown below that such a correction, often introduced by

qualitative reasoning, has indeed a theoretical basis.

Depending on the system, the magnitude of such corrections may be

largely diﬀerent. Fig. 14.2 illustrates the behavior of Q for systems exhibiting

diﬀerent thermodynamic situations. Thermodynamic ideality may be deﬁned

by Raoult’s law, which implies that Q = 1. Examples for this type are binary

mixtures of rare gases, or hydrocarbons. Fig. 14.2 shows data for n-hexane +

n-dodecane mixtures, where Q is indeed very close to unity. Model calcula-

tions show that, to a ﬁrst approximation, binary mixtures of Lennard-Jones

ﬂuids are ideal as well [6] . Thus, for ideal mixtures the correction does not

play a role at all. The same is true for suﬃciently dilute solutions, because

for x

→ 0andx

→ 0 we have by deﬁnition Q → 1.

Systems with aggregation between dislike components show negative de-

viations from Raoult’s law and one ﬁnds Q>1. This behavior is illustrated in

Fig. 14.2 for mesithylene + carbon tetrachloride. In contrast, self-aggregation

of the components reﬂects itself by positive deviations and 0 <Q<1. Ex-

amples are solutions of alcohols or carboxylic acids in comparatively inert

solvents such as carbon tetrachloride. Fig. 14.2 shows, as an example, data

for methanol + carbon tetrachloride, where in parts of the concentration

562 Hermann Weing¨artner

1.50

0 0.2

0.4

0.6

0.8

0.50

(1)

(2)

(3)

Fig. 14.2. Composition dependence of the thermodynamic factor Q in the systems

mesithylene + carbon tetrachloride (1), n-hexane + n-dodecane (2), and methanol

+ CCl

(3) at 298.15 K. The ﬁrst-mentioned components are denoted as compo-

nent 1.

range Q diﬀers by more than an order of magnitude from unity. Thus, ther-

modynamic non-ideality enhances diﬀusion in the case of negative deviations

of Raoult’s law and slows down diﬀusion for positive deviations of Raoult’s

law.

In view of these reasonings one often reformulates the Darken relation (2)

=(x

+ x

) Q. (14.10)

In the case of thermodynamically non-ideal systems, an incorporation of the

thermodynamic factor often leads to an improved estimate of D

in compar-

ison with Darken’s original relation (14.2). In fact, in most cases the Darken

relation is applied in the form of (14.10) rather than (14.2). We show in

0 0.2

0.4

0.6

0.8

10 D/m s

1

Fig. 14.3. Composition dependence of diﬀusion coeﬃcients in the system n-hexane

(1) + n-dodecane (2) at 298.15 K: D

(open circles), D

(squares), D

(ﬁlled

circles). n-hexane is component 1.

14 Mutual Diﬀusion in Mixtures 563

1.75

1.25

1.50

0 0.2

0.4

0.6

0.8

10 D/m s

2 1

Fig. 14.4. Composition dependence of diﬀusion coeﬃcients in the system methanol

(1) + carbon tetrachloride (2) at 298.15 K: D

(squares), D

(open circles), D

(ﬁlled circles).

Fig. 14.3 diﬀusion data for the near-ideal system n-hexane + n-dodecane [4].

Equation (14.10) represents the experimental data for D

practically within

the limits of experimental uncertainty.

However, even in this improved form, the Darken equation is of little use

for predicting diﬀusion data for systems with comparatively strong speciﬁc

interactions between the components. We show in Fig. 14.4 experimental

data for methanol + carbon tetrachloride [27] with strong self-aggregation

of methanol molecules. Fig. 14.5 shows that (14.2) overestimates D

more than a factor of two in parts of the concentration range. If (14.10)

is used instead, D

is largely underestimated. Near the minimum of D

experimental and predicted data diﬀer by an order of magnitude.

(14.2)

(14.10)

Fig. 14.5. Estimate of mutual-diﬀusion coeﬃcients in the system methanol +

carbon tetrachloride by (14.2) and (14.20), respectively. Methanol is component 1.

564 Hermann Weing¨artner

Finally, we note that in thermodynamics (14.8) is just a measure for the

thermodynamic stability of mixtures, because the thermodynamic stability

condition for mixtures can be rewritten in terms of Q, leading to Q>0. In

other words, the spinodal line for liquid-liquid phase separation is deﬁned

by Q = 0. This stability criterion is therefore often denoted as condition for

diﬀusional stability. As a consequence, when approaching the spinodal line,

mutual diﬀusion slows down, because the driving force vanishes. Very slow

diﬀusion in systems of comparatively low viscosity may therefore imply that

one is close to phase separation or to a critical point. This observation is well

established experimentally for systems with liquid-liquid phase separations

like triethylamine + water [28] or n-hexane + nitrobenzene (see Fig. 15.14

of Chap. 15).

14.4 Thermodynamics of Mutual Diﬀusion

By using the thermodynamics of irreversible processes, transport phenomena

can be described in a uniﬁed formalism [1, 29, 30]. This type of approach is

particularly adequate, when seeking for a starting point for a microscopic

description of transport phenomena. Again, it is necessary to deﬁne a ref-

erence frame to which the ﬂuxes are referred to. Although, in principle, the

equations of the thermodynamics of irreversible processes can be set up in

any of these frames, the desired interconnection with statistical mechanics

suggests to do this analysis in the barycentric frame with the center-of-mass

at rest.

To transform Fick’s law to the barycentric frame we ﬁrst introduce the

partial mass densities of the components as !

= m

/V . Moreover, we consider

speciﬁc chemical potentials deﬁned by the mass derivative of the Gibbs free

energy, µ

∗

, rather than chemical potentials deﬁned as partial molar quantities.

Then, Fick’s law may be formulated as

−J

= D

grad !

and

−J

= D

grad !

. (14.11)

Superscript m indicates quantities deﬁned in the barycentric frame. Pro-

cedures for reference-frame transformation are extensively discussed in the

literature [1, 29, 30]. Detailed analysis shows that the diﬀusion coeﬃcients

and D

are not equal, but interrelated by

= D

. (14.12)

However, within the framework of thermodynamics of irreversible processes,

the gradient of the partial mass density is not a suitable driving force. To

derive the correct force we consider linear equations between ﬂuxes J

and

forces X

of the form

14 Mutual Diﬀusion in Mixtures 565

−J

+···

−J

+···

−J

+···

(14.13)

Thermodynamics of irreversible processes says that the ﬂuxes and forces have

to be chosen in such a way that their product is equal to the entropy pro-

duction Tσ of the system. In the latter case the coeﬃcients L

in (14.13) are

called phenomenological coeﬃcients. One can show that in the barycentric

system the entropy production is given by [1, 29, 30]

Tσ = −J

grad (µ

∗

− µ

∗

) (14.14)

or an analogous expression for the ﬂow of component 2. Thus, the correct

driving force is the gradient of the speciﬁc chemical potential. In a binary

system the phenomenological equations are then given by

−J

= L

grad µ

∗

+ L

grad µ

∗

−J

= L

grad µ

∗

+ L

grad µ

∗

. (14.15)

There are, however, two restrictions among the ﬂuxes and forces. First, the

ﬂuxes are not independent. If the local center-of-mass is at rest we have

+ J

= 0 (14.16)

which represents the analogue to (14.5). Furthermore, the Gibbs-Duhem

equation interrelates the speciﬁc chemical potentials through

grad µ

∗

+ !

grad µ

∗

=0. (14.17)

It can be shown [1, 29, 30] that these restrictions lead to the condition

= L

= −L

. (14.18)

Thus, information on the mutual-diﬀusion coeﬃcient is suﬃcient to determine

all four phenomenological coeﬃcients. This simplicity is, however, lost in

systems composed of more than two components. In detail, one ﬁnds

= −

+ x

)



dlna

dlnx



. (14.19)

is the molecular mass of component i.

Let us brieﬂy consider this situation from a more general point of view.

In a system of r components there are r forces and r ﬂuxes described by

the phenomenological relations (14.13). Accordingly, one obtains a matrix of

phenomenological coeﬃcients

566 Hermann Weing¨artner

⎛

⎜

⎝

···L

⎞

⎟

⎠

. (14.20)

The coeﬃcients of this matrix are not independent, because the gradients of

the chemical potentials are interrelated by the Gibbs-Duhem relation and the

sum of the ﬂuxes has to be zero. For a binary system these restrictions lead

directly to (14.18). For ternary and higher-order systems these conditions

are not suﬃcient to determine the matrix. There is, however, an additional

postulate, saying that the matrix of the coeﬃcients has to be symmetric, i.e.

= L

. (14.21)

This is Onsager’s well-known reciprocity relation which, in a molecular pic-

ture, reﬂects microscopic reversibility. Thus, in general, in a system of r

components there are only r · (r − 1)/2 independent coeﬃcients.

Now, for a binary system with r = 2 we are back to a single diﬀusion

coeﬃcient. However, for a ternary system, presuming the reciprocity relation,

we have already three independent diﬀusion coeﬃcients. If, however, one

aims at proving the Onsager relation rather than implementing this relation

in data analysis, one has to extract four coeﬃcients from the experimental

concentration distribution [1, 20].

One of the pressing questions is of course, whether the cross terms of the

matrix with i = j are suﬃciently diﬀerent from zero to be of importance in

data analysis. Otherwise, the analysis is largely simpliﬁed. In fact, in many

models for diﬀusion in complex systems, approximations are made which

implicitly imply that the cross terms are negligible. However, in this regard

the answer by accurate experiments is desillusioning: The cross terms may

be even larger in magnitude than the main terms [22,23].

Finally, we consider brieﬂy systems with charged species such as elec-

trolyte solutions or molten salt mixtures. Thermodynamically, an electrolyte

solution consisting of the salt (s) and water (w) is a binary system with a

single mutual-diﬀusion coeﬃcient D

, because diﬀusion arises from the gra-

dients of the neutral salt and water. There cannot be gradients of single ions,

because the concentrations of the ions are not independent variables, but are

interrelated by the constraint of overall charge neutrality. Then, with regard

to mutual diﬀusion there is a set of four Onsager coeﬃcients, which according

to (14.18) are interrelated by

= L

= −L

(14.22)

However, one can also try to apply the formalism of the thermodynam-

ics of irreversible processes to a ternary system consisting of the cation (c),

anion (a) and the solvent water (w). (Note that the three self-diﬀusion co-

eﬃcients of the ionic constituents can indeed be measured separately.) Such

14 Mutual Diﬀusion in Mixtures 567

a formalism yields a 3 × 3 matrix of Onsager coeﬃcients. We denote these

coeﬃcients by l

(i, j = c,a,w). It is an intriguing problem to relate the l

of the ternary model system to the L

of the salt-water system obtained by

direct thermodynamical analysis.

By symmetry, only three of the nine l

of the 3×3 matrix are independent.

Obviously, in addition to the mutual-diﬀusion coeﬃcient, two other exper-

imental quantities are needed for determining the l

. The solution of this

problem is given by the fact, that thermodynamics of irreversible processes

relates two other transport coeﬃcients to the l

[29, 30], namely the ionic

mobilities of the cations and anions in the electric ﬁeld. These can be deter-

mined directly, for example, by the new technique of electrophoretic NMR

discussed in Chap. 17. Traditionally, one measures, however, the electrical

conductance of the solution and the transference numbers that allow to sep-

arate the conductance into single-ion contributions. The resulting formalism

to determine the Onsager coeﬃcients l

has been worked out in detail long

time ago by Miller [31].

14.5 Linear Response Theory and Time Correlation

Functions

In statistical mechanics the time dependence of the dynamical variables of

N-particle systems are described by Hamilton’s equations of motion. These

can, for example, be solved for some hundreds or thousands of particles by

numerical solution in molecular dynamics simulations ([2] and Chap. 23). Self-

diﬀusion coeﬃcients can then be derived from the simulated trajectories, e.g.

via (14.1).

For an analytical description it is only possible to consider certain time

and ensemble averages. For this purpose one considers the time dependence

of the N-particle correlation function ( [6,32], see also Chap. 23)

, p

where r

and p

stand symbolically for the generalized position and mo-

mentum vectors of the N-particle system. At equilibrium, this correlation

function is given by

=const· exp(−H

/kT ), (14.23)

where H

is the classical Hamiltonian of the N-particle system. If there is

a weak perturbation due to an external force, the Hamiltonian contains an

additional contribution H

ext

, i.e. H

is replaced by

H = H

+ H

ext

. (14.24)

In this case, the time dependence of the correlation function is given by

Liouville’s equation

568 Hermann Weing¨artner

∂F

∂t

= iLF

, (14.25)

where

L=i





∂H

∂p



∂

∂r



−



∂H

∂r



∂

∂p



(14.26)

is the Liouville-Operator. If H

ext

is known, one can calculate expectation

values of the dynamical variables due to this perturbation. In the case of

diﬀusion the perturbation is related to a local gradient in the speciﬁc chemical

potential.

In the regime of linear response due to suﬃciently weak perturbations,

the application of this formalism shows that any transport coeﬃcient A can

be written as an integral over a time correlation function of the form [6,32]

A ∝

∞



J

(0) · J

(t)dt, (14.27)

where J

(τ) is the ﬂux associated with A at time τ =0andt, respectively.

Expressions of this type are denoted as Green-Kubo relations.

Probably the most well-known and most simple example of a Green-Kubo

relation is the expression for the self-diﬀusion coeﬃcient D

in terms of the

velocity auto-correlation function

∞



v

a,α

(0) · v

a,α

(t)dt, (14.28)

where the velocity of a particle α of component a at time t = 0 is correlated

with that of the same particle at time t. These velocities refer to the barycen-

tric reference frame. Because self-diﬀusion does not lead to macroscopic gra-

dients in the system, the barycentric frame coincides with the volume- and

laboratory-ﬁxed frames. In other words, the self-diﬀusion coeﬃcient is inde-

pendent of the reference frame.

By using the proper relation between position vectors and velocities one

can show that (14.28) is fully equivalent to the relation for the self-diﬀusion

coeﬃcient in terms of the mean square displacement, (14.1). For example,

when determining the self-diﬀusion coeﬃcient in molecular dynamics simu-

lations it is only a technical problem, whether the self-diﬀusion coeﬃcient is

extracted via (14.1) or (14.28) [2] (see also Chap. 23).

Moreover, another equivalent expression may be mentioned which is par-

ticularly suitable when monitoring diﬀusion processes in neutron scattering

experiments (see Chaps. 2, 3, and 13). In this case, the quantity of inter-

est is the Van Hove dynamic structure factor S(κ, ω), where κ and ω refer

to the momentum and energy transfer in the scattering experiment. If one

rewrites (14.1) in terms of S(κ, ω) one ﬁnds the self-diﬀusion coeﬃcient to be

14 Mutual Diﬀusion in Mixtures 569

related to the hydrodynamic (κ → 0,ω→ 0) limit of the self-part of the dy-

namical structure factor S

(κ, ω) which is available by incoherent scattering

experiments [6]

= π lim

ω→0

lim

κ→0

(κ, ω) . (14.29)

In fact, it is well-known that in the hydrodynamic limit incoherent neutron

scattering leads to a Lorentzian spectrum with a half-width determined by

the self-diﬀusion coeﬃcient [6] (see also Chap. 3).

14.6 The Time Correlation Function for Mutual

Diﬀusion

In order to obtain the equivalents to (14.1), (14.28), and (14.29) for mutual

diﬀusion, the Green-Kubo theory has to be applied to the phenomenological

coeﬃcients L

. The result is [32]

=(3kTV )

−1

∞



J

(0) · J

(t)dt, (14.30)

where J

is the microscopic mass ﬂow of species i = a or b in the barycentric

frame. This mass ﬂow has to be summed up over the velocities of all particles

of component i:

(t)=



k=1





i,k

(t); i = a, b. (14.31)

We consider ﬁrst the expression for L

in the case of which a =1and

b = 2. Then, according to (14.30) the velocities of the species of component 1

are coupled to those of the species of component 2. If (14.31) is inserted

into (14.30) one obtains an expression involving velocity cross-correlations for

particles of diﬀerent components, in contrast to the velocity auto-correlation

function entering into the expression for the self-diﬀusion coeﬃcient.

Alternatively, we may consider the coeﬃcient L

(or, by interchange of

indices, L

), instead of L

. Then, the situation turns out to be diﬀerent.

After inserting (14.31) into (14.30) and expanding the sums, we can sort out

two diﬀerent types of terms: In the ﬁrst type, the velocity of a particle α of

component 1 (or 2) at time zero is correlated with that of the same particle α

at time t. However, there are also contributions, which correlate the velocity

of a particle α of component 1 (or 2) with that of a distinct particle β of the

same component. This suggests to split up L

(and L

) into a contribution

from a velocity auto-correlation function plus a contribution from velocity

cross-correlations of distinct particles of the same component. We note that