Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

590 Alfred Leipertz and Andreas P. Fr¨oba

Fig. 15.6. Possible setup for a dynamic light scattering experiment.

of two circular stops, onto a detector, conventionally a photomultiplier tube.

The signal is ampliﬁed, discriminated and fed into the correlator, a special

purpose computer for the computation of the ACF. After this generalized

scheme the individual parts shall be given some more discussion.

Laser

The choice of the suitable laser, which should be linearily polarized with

orientation of the E vector perpendicular to the scattering plane for usual

applications, is mainly determined by the scattering cross section of the ﬂuc-

tuations to be investigated. Low-power He-Ne or semiconductor lasers are

in most cases suﬃcient for measurements of particle diﬀusion coeﬃcients or

phenomena close to critical points. More powerful lasers with an output of

typically several hundreds of milliwatts are required for measurements, e.g.,

of the thermal diﬀusivity, where conventionally Argon lasers have been used,

but where also more recent types of solid-state lasers may be employed.

Which laser may be used also depends on the detection scheme applied.

In heterodyne detection the reference beam has to be added coherently on

the detector. Thus, the coherence length of the laser must be large enough to

ensure that the experiment is not aﬀected by possibly diﬀerent path lengths

of the main and the reference part of the light. The laser should therefore only

exhibit a single longitudinal mode, which may be accomplished by inserting

an intra-cavity etalon into gas lasers.

15 Diﬀusion Measurements in Fluids by Dynamic Light Scattering 591

Illuminating Optics

Generally, an important feature of the illuminating optical system is that

the laser beam should be focused strongly [12, 13], as it can be shown that

the signal-to-noise ratio may be improved by reducing the spot size of the

laser. Basically, the increased irradiance is balanced by the reduced size of

the scattering volume, but as it is possible to reduce the size of stops in the

receiving system simultaneously, a net eﬀect results. The major disadvantage

or limitation of focusing is the lack of deﬁnition in the scattering vector,

as now - in a simpliﬁed picture - light is incident from various angles, which

results in an overlay of several correlation functions. This point is very critical

for the measurement of the sound attenuation and will be discussed below.

The scattering vector and thus the scattering angle to be reasonably em-

ployed are mainly determined by the process to be investigated. Small scatter-

ing angles result in a small linewidth and accordingly in a comparatively long

decay time. For a DLS analysis especially of the Brillouin lines it is necessary

to realize a small scattering angle in order to obtain reasonable time scales

in the computation of the ACF and for signal statistics. Conversely, slow

diﬀusion processes like particle diﬀusion are favourably analysed with large

scattering angles up to a backscattering geometry. For a survey, linewidths

and decay times for various scattering angles are given in Table 15.1 for the

individual processes and liquid values, which may be regarded as typical in

the order of magnitude.

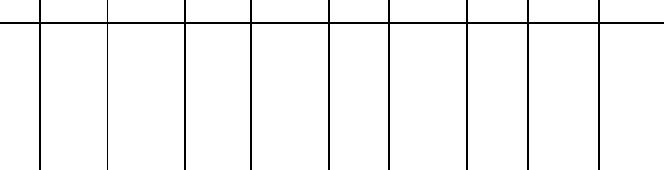
For the determination of the scattering vector the refractive index of the

sample must be known which is in general not found tabulated for all samples,

thermodynamic states, and wavelengths used. One can solve this problem by

actually measuring the refractive index by using the refractions between the

external medium and the sample [14, 15]. Another possibility is to make use

of the approximation sin (Θ

/2) ≈ (1/2) sin Θ

and to replace, according to

Snell’s law, the resulting term n sin Θ

in the expression for the scattering

vector by sin Θ

,whereΘ

is the external angle of incidence and the refractive

index of the surrounding medium is assumed to be 1 (cf. Fig. 15.7). This

Table 15.1. Typical values for linewidths and decay times in the Rayleigh-Brillouin

spectrum. For the Rayleigh lines the subscripts denote thermal diﬀusivity (t), mu-

tual diﬀusion (12) and particle diﬀusion (p).

q/m

−1

◦

5.8·10

682 kHz 1.5 µs 14 kHz 73 µs 682 Hz 1.5 ms 1.4 Hz 730 ms

◦

1.5·10

4.3 MHz 235 ns 85 kHz 12 µs 4.3 kHz 235 µs 8.5 Hz 117 ms

◦

5.8·10

68 MHz 15 ns 1.4 MHz 740 ns 68 kHz 15 µs 135 Hz 7.4 ms

◦

2.4·10

1.1 GHz 0.89 ns 22 MHz 45 ns 1.1 MHz 892 ns 2.2 kHz 446 µs

180

◦

3.3·10

2.2 GHz 0.45 ns 45 MHz 22 ns 2.2 MHz 446 ns 1.1 kHz 223 µs

592 Alfred Leipertz and Andreas P. Fr¨oba

Fig. 15.7. Determination of the modulus of the scattering vector in the small-angle

approximation.

approximation is very useful for small scattering angles [16], but naturally

cannot be used for larger ones.

An exact solution, which may be used for all scattering angles, is a spe-

cial symmetrical setup of the experiment [13]. Again, the a priori unknown

quantities (sample refractive index and scattering angle) may be replaced by

the refractive index of the surrounding medium and the angle of incidence.

Sample Cell

The range of possible sample cells is very broad due to the variety of appli-

cations, and the actual choice depends on the scattering angle and the path

length within the cell to be used. For small scattering angles typically cylindri-

cal cells are employed, where the main body may be made of metal for higher

pressure applications, and optical access is provided through cylindrical en-

trance and exit windows. If larger scattering angles are needed, especially for

the measurement of particle diﬀusion coeﬃcients, glass cuvettes with circu-

lar or rectangular cross sections are normally employed, where appropriate

modiﬁcations with the use of glass rings are done for measurements at higher

pressures. An important feature in many DLS systems is the use of an index-

matching ﬂuid, i.e. of a liquid with a refractive index very close to that of the

glass materials employed, in order to suppress unwanted reﬂections. A more

extensive treatment of sample cell design with some speciﬁc examples may

be found in [8].

Detection Optics

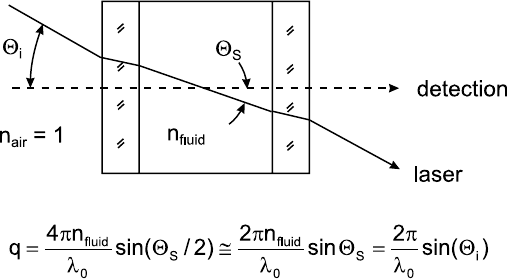
As DLS probes the temporal evolution of the interference pattern caused by

ﬂuctuations in a sample, it is essential to restrict the solid angle of detection in

15 Diﬀusion Measurements in Fluids by Dynamic Light Scattering 593

Fig. 15.8. Model for the coherence properties of the detection system; “full” spatial

coherence is achieved if the detector area A

is smaller than the coherence area A

coh

a way that the pattern of bright and dark speckles is not averaged out. Thus,

the receiving system must ensure that the degree of coherence is large enough

for a good modulation of the signal. In the simplest way, the choice of the

solid angle of detection is realized by two circular stops at a given distance

where the complex degree of coherence determining the contrast b in the

correlation function (15.24) is a function of stop diameter and distance [12]

(cf. Fig. 15.8). Recent approaches employ single-mode optical ﬁbres, which

make use of the fact that only one mode of ﬁeld is propagated and thus

enables a perfectly coherent registration [17].

Detector

The standard detector for DLS measurements is a photomultiplier tube,

which is operated in a photon-counting mode, i.e. it produces a stream of

pulses the frequency of which is proportional to the light ﬂux impinging on

it. A fundamental problem encountered in the detection system is that pho-

tomultipliers give rise to spurious signals, e.g., there is an afterpulsing eﬀect,

meaning that with a certain probability a detected photon may cause an-

other subsequent pulse with no relevance for the process investigated. An

elegant solution to get rid of this problem is to use a beam splitter just in

front of the detector, to employ two photomultipliers (see Fig. 15.6) instead

of a single one and to operate these in a cross-correlation mode [18]. This

approach ensures that there is only correlation for events both detectors see

simultaneously and spurious uncorrelated pulses in either photomultiplier are

594 Alfred Leipertz and Andreas P. Fr¨oba

not registered. This cross-correlation scheme turns out to be necessary when

fast ﬂuctuations on a time-scale of microseconds and below are investigated,

but should not be employed with no actual need for it, as the signal usable is

reduced by a factor of two. An alternative to photomultipliers are avalanche

photo diodes, which must be operated in a special way and which exhibit a

higher quantum eﬃciency at longer wavelengths [19].

Correlator

Correlators are special-purpose computers which calculate correlation func-

tions in real-time. An important characteristic of correlators is the sample

time ∆τ, which is the time interval used to collect the detector pulses and

which determines the resolution of the correlation function. In former times,

correlators were bulky stand-alone machines with typically some hundred

channels with an identical sample time (single-tau structure). Today, cor-

relators are made in form of plug-in-cards for PCs, and, what is more im-

portant, they oﬀer a more sophisticated scheme of sample-time distributions

(multiple-tau structure). A possible selection is that after a block of eight or

sixteen channels with a constant sample time, ∆τ is doubled after each subse-

quent block. With this quasi-logarithmic channel spacing, sample times span

a range from a few nanoseconds up to many seconds so that it is possible to

measure processes on a completely diﬀerent time-scale simultaneously. With

the evolution of standard PCs it is also possible to use a fast data-acquisition

board and to compute the ACF by a normal software routine; sample-times

of nanoseconds, however, are still far away from realization in this way.

15.3.2 Signal Statistics and Data Evaluation

With DLS experiments one should always be well aware that one is prob-

ing statistical ﬂuctuations. Therefore it is necessary to average over a large

number of independent events in order to be able to extract reliable informa-

tion from the ACF. It is thus essential to discuss the statistical properties of

correlation functions. Let us ﬁrst consider the variance σ

of the correlator

channel i of a homodyne ACF, where x is the lag-time of the correlator chan-

nel in units of the decay time of the intensity ACF, i.e. x = τ/τ

, f is the

count rate, i.e. the number of detector pulses per second, and T is the total

duration of the experiment. With these abbreviations, the variance may be

approximately expressed by [20, 21]





[1 + exp(−2x)(2x +1)+2b exp(−2x)(−2x − 3)

+8b exp(−x)] + 2b

−1

[1 + exp(−2x)+2b exp(−x)]

+ b

−2

∆τ

−1

[1 + exp(−x)]

(15.27)

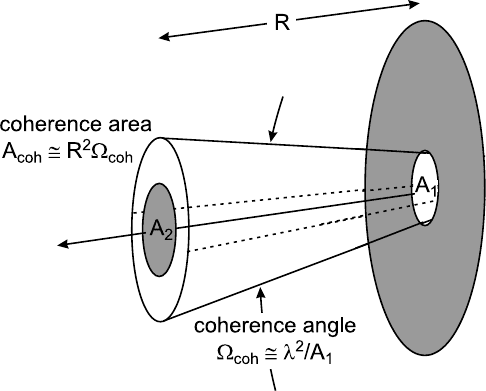
15 Diﬀusion Measurements in Fluids by Dynamic Light Scattering 595

Fig. 15.9. Standard deviation of the ACF at τ = τ

as a function of count rate

and decay time; here a correlator with a quasi-logarithmic sample time structure

has been assumed.

In this relationship the various sources of noise in correlation functions may

be identiﬁed. The ﬁrst line reﬂects the statistical nature of the experiment

itself; this signal noise is proportional to the ratio of decay time and mea-

surement time and thus is reduced when averaging over a larger number of

independent events. The second line is a cross term, whereas the third line

reﬂects the imperfect detection, as photons impinging onto the detector only

result in a detected pulse with a certain probability given. This detection

noise dominates for small values of count rate and sample time; in this case

the channel variance is inversely proportional to ∆τ. This formula has some

consequences for the design of an experiment. Firstly, the scattering angle

should be chosen in a way that the resulting decay time is not too small in

order to ensure that during a sample time of interest there is a large number

of detected pulses to keep the detection noise at a low level. On the other

hand, if decay times are very large, little can be gained by increasing the

count rate of the experiment, e.g., by increasing the laser power, as in this

case the statistical nature of the experiment itself dominates. This saturation

eﬀect is visualized in Fig. 15.9, where the standard deviation of the channel

at a lag time of one τ

, i.e. x = 1, is plotted against the count rate for various

values of τ

A central quantity for the evaluation of correlation functions is the decay

time τ

. In order to be able to extract this quantity with high accuracy, it

is desirable to ensure experimental conditions where the ACF takes the form

of a simple exponential. A curve of form y = a + b exp(−τ/τ

) is then ﬁtted

to the experimental ACF, which may be done using a non-linear algorithm

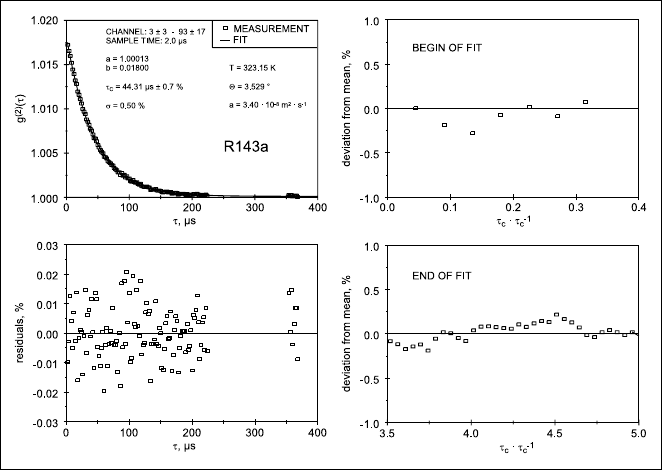
596 Alfred Leipertz and Andreas P. Fr¨oba

Fig. 15.10. Example for the multi-ﬁt approach for the evaluation of correlation

functions taken at the refrigerant R143a in the saturated liquid phase (insert on

top left). The insert on bottom left shows the residuals of experimental data and

ﬁt, which is free of systematic deviations. The inserts on top and bottom right show

the deviation of the decay times determined from the mean value, when the ﬁt is

started at diﬀerent times and is performed up to diﬀerent lag times, respectively.

according to Marquard and Levenberg [22] and which requires to attribute

a correct statistical weight w

to each data point according to w

=(1/σ

)

In this context it is of great importance to make sure that the correlation

function actually matches the theoretical model; if this does not hold there

is a clear indication that the experiment cannot be relied on. A possible way

to perform this check is to transform the experimental correlation function

according to g

(2)

(τ) → ln[g

(2)

(τ) −1] and to ﬁt a polynom to this expression.

In this method of cumulants [23] all orders higher than linear should vanish

for a pure exponential and from the quadratic and the linear coﬃcient a

quality factor may be built up to quantify deviations. However, there are two

major problems connected with this approach. Firstly, it relies on a value

of exactly one for the baseline; even small deviations, which may not aﬀect

the measurement in the time interval of interest, may result in erroneously

bad values for the quality factor. Secondly, the transformation is basically

restricted to positive values of g

(2)

(τ) −1; with experimental noise given, the

cumulant expansion is restricted to a limited interval of lag times.

15 Diﬀusion Measurements in Fluids by Dynamic Light Scattering 597

A diﬀerent approach, which overcomes these problems, is to ﬁt an ex-

ponential to various lag time intervals [21]. The experimental ACF is only

regarded to match the theoretical form if the decay times obtained for these

diﬀerent intervals agree within a certain value given. Moreover, the standard

deviation of the single ﬁt may be regarded as a measure of quality, which

takes into account both the statistical quality of the experimental data and

possible systematic deviations. An example for this procedure is given in

Fig. 15.10.

Another important question is that for the time interval that should be

employed for the ﬁt. If too many channels at large lag-times are omitted, there

will be a signiﬁcant loss of information; if the ﬁt is extended too much into

the background, noisy data without relevance are included. For the multi-ﬁt

procedure it has turned out to be advantageous if a span of about 2−6 decay

times is regarded in the evaluation. This ensures that all relevant information

is included and that possible deviations from a single exponential can be

detected reliably.

15.4 Thermophysical Properties of Fluids Measured by

Dynamic Light Scattering

15.4.1 Thermal Diﬀusivity

The thermal diﬀusivity a is that transport property for which the devel-

opment of the DLS technique is probably most advanced and where mea-

surements can be carried out routinely over a wide range of temperature

and pressure for the liquid phase and, due to the lower signal levels, in an

extended vicinity of the critical point for the vapour phase [24–30]. What

makes the measurement of the thermal diﬀusivity particularly interesting is

the fact that it is hardly possible by any other technique than light scattering

to measure this property directly with comparable accuracy. Other methods

access the thermal conductivity λ = aρc

, which is related to the thermal

diﬀusivity a by the density ρ and the isobaric heat capacity c

With the exception of measurements in the vicinity of the critical point,

normally a heterodyne detection scheme is employed so that the correlation

function takes the simple form of (15.25). As the measurement of the thermal

diﬀusivity is performed at low scattering angles of about 2.5

◦

to 5

◦

an ac-

curate measurement of the angle of incidence is of major importance, which

may be performed by an autocollimation procedure. The main measuring de-

vice is a rotation table, which is placed above the sample cell. With a mirror

mounted on this table the laser beam can be reﬂected into the direction of

the source of the laser beam. First the optical axis of observation is deﬁned

by aligning the laser beam through the stops, and the angle value is mea-

sured by autocollimation. Next the laser beam is adjusted to the angle of

incidence desired, and after another autocollimation the angle of incidence

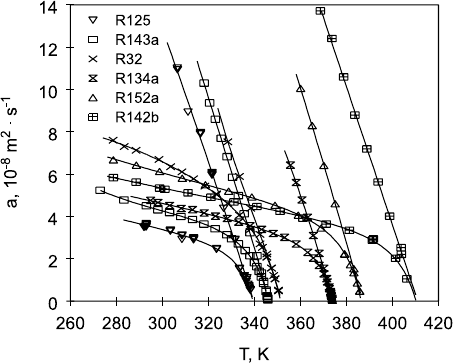
598 Alfred Leipertz and Andreas P. Fr¨oba

Fig. 15.11. Thermal diﬀusivity of selected refrigerants on the saturation line [29,

30]; lower trace symbols: liquid; upper trace symbols: vapour.

can be obtained from the diﬀerence of the readings on the rotation table.

With an uncertainty in the angle measurement of order 0.01

◦

an uncertainty

in the thermal diﬀusivity of about 0.5% to 1% results.

The other major source of error is the determination of the decay time.

If the correlation function is free from systematical errors the uncertainty in

the determination of τ

is given by the signal and the experimental dura-

tion. Depending on the equipment used, the scattering cross section of the

ﬂuctuations investigated and the time available for an experimental run, the

uncertainty for a single measurement is of order 1 − 3%. If several indepen-

dent experimental runs are performed, which is superior to running a single

experiment over a longer time, this value may of course be improved. Finally,

the uncertainty also depends on the deﬁnition of the thermodynamic state,

especially on the exact measurement of the sample temperature. In conclu-

sion, a total single-measurement uncertainty of 2.5%, as it was derived for

measurements on liquid toluene [27], may be regarded as typical.

There have been many applications on the determination of a for a wide

range of ﬂuids. DLS has especially contributed to an improvement in the data

situation for refrigerants. An example is given in Fig. 15.11, where measure-

ments on new refrigerants with less environmental impact are shown.

Whereas the measurement of a in pure ﬂuids is basically a straightforward

task, this is clearly more diﬃcult in ﬂuid mixtures. Even in the simplest case

of a binary ﬂuid mixture and neglecting the Brillouin component, the ACF

takes the form

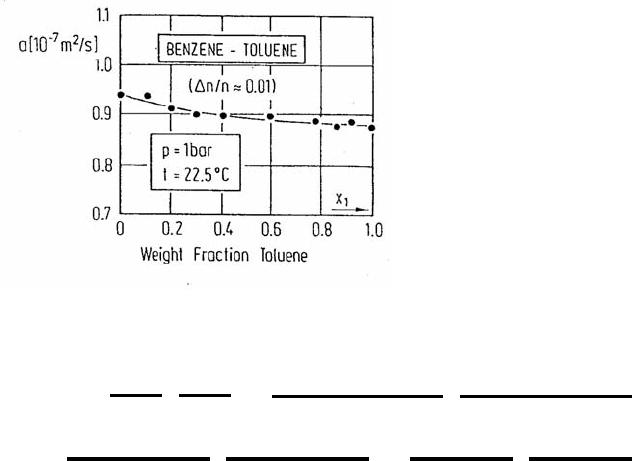
15 Diﬀusion Measurements in Fluids by Dynamic Light Scattering 599

Fig. 15.12. Thermal diﬀusivity of a mixture of benzene and toluene [31].

(2)

(τ)=(I

+ I

)

  

background

+2I

exp(−τ/τ

C,t

)+2I

exp(−τ/τ

C,c

)



 

heterodyne term

exp(−2τ/τ

C,t

)+I

exp(−2τ/τ

C,c

)



 

homodyne term

+2I

exp(−τ/τ

C,t

− τ/τ

C,c

)



 

cross term

(15.28)

where the subscripts t and c denote the contributions from temperature and

concentration ﬂuctuations, respectively. With a large reference light contribu-

tion, I

 I

and I

 I

, the ACF simpliﬁes to a sum of two exponentials

(2)

(τ)=a + b

exp(−τ/τ

C,t

)+b

exp(−τ/τ

C,c

). (15.29)

It is obvious that even for this simpliﬁed function the determination of the

decay time τ

C,t

is more complicated and associated with a higher degree of

uncertainty than in the case of a pure ﬂuid, because a larger number of para-

meters are to be ﬁtted. The situation becomes easier if the refractive indices

of the two components nearly match, as the signal from the concentration

ﬂuctuations may then be treated as a low-amplitude perturbation. A pos-

sible approach [31] is to expand the exponential decay of the concentration

ﬂuctuations in a way that an ACF of form

(2)

(τ)=a + b exp(−τ/τ

C,t

)+cτ (15.30)

results. The thermal diﬀusivity of a mixture of benzene and toluene measured

in that way is shown in Fig. 15.12.

It is also possible to measure a in mixtures with a larger diﬀerence in

refractive index. Naturally, this is connected with a loss of accuracy and

comes to a limit, when the signal due to temperature ﬂuctuations is much

weaker than that by concentration ﬂuctuations.