Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

580 Alfred Leipertz and Andreas P. Fr¨oba

temporal analysis of scattered light, and gives additionally some informa-

tion on related techniques, namely surface light scattering (SLS), where light

scattered from liquid/vapour interfaces is analysed, and forced Rayleigh scat-

tering (FRS), where an additional thermal grating is employed. It is a revised

and signiﬁcantly extended version of the chapter published in the ﬁrst edition

of this textbook [6].

15.2 Basic Principles

15.2.1 Spectrum of Scattered Light

When coherent light in form of a plane wave E

= E

exp[i(k

r − ω

t)] with

electric ﬁeld amplitude E

, wave vector k

, and frequency ω

impinges on an

isotropic ﬂuid sample with permittivity , the scattered ﬁeld at a suﬃciently

large distance R from the scattering volume V with electric susceptibility

ﬂuctuations ∆χ

is found to be (for details, see, e.g., Chap. 16 and [7,8])

(R,t)=k

× (k

× E

)







exp [i(k

R − ω

t)]

4πR



∆χ



,t) exp [i(k

− k



]dr



(15.1)

Here, 

denotes the permittivity in vacuo, and k

the wave vector of the

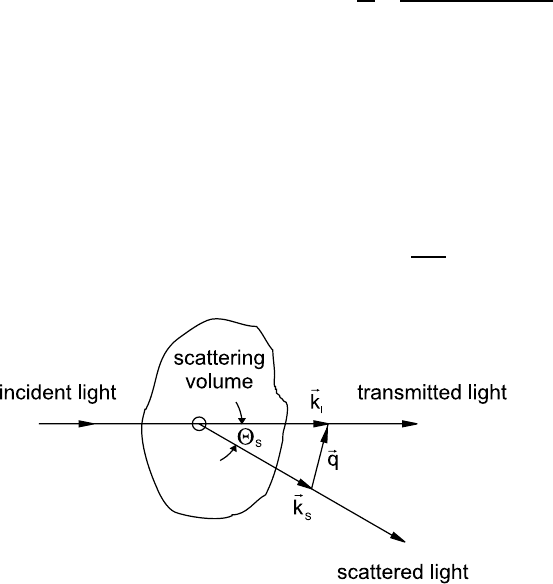
scattered light. By the diﬀerence between the wave vector of the incident

light and that one of the scattered light the scattering vector q = k

− k

deﬁned. For a quasielastic scattering process, i. e. for k

∼

, the modulus

of the scattering vector directly follows from the geometry, see Fig. 15.1,

q = |k

− k

∼

sin(Θ

/2) =

4πn

sin Θ

/2, (15.2)

Fig. 15.1. Scattering geometry.

15 Diﬀusion Measurements in Fluids by Dynamic Light Scattering 581

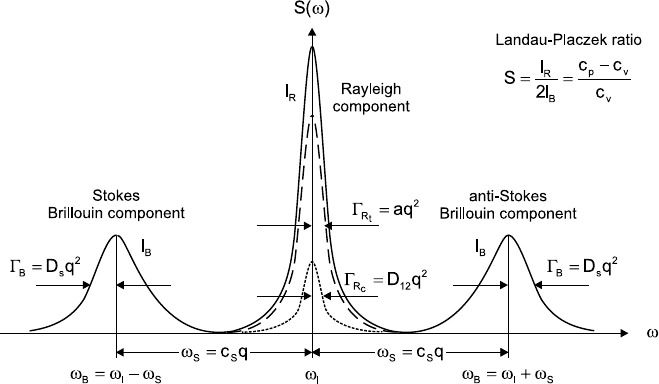
Fig. 15.2. Schematic representation of the spectrum of scattered light for a binary

ﬂuid mixture.

where n is the refractive index of the ﬂuid, λ

is the wavelength of the light

in vacuo, and Θ

is the scattering angle.

It is the key feature of the DLS technique to analyse the ﬂuctuations in the

electric susceptibility ∆χ

. In a ﬂuid in macroscopic thermodynamic equilib-

rium, the local statistical ﬂuctuations in the electric susceptibility are caused

by microscopic ﬂuctuations of temperature (or entropy), of pressure, and of

species concentration in mixtures. The relaxations of these statistical ﬂuctu-

ations follow the same rules which are valid for the relaxation of macroscopic

systems. Thus, the decay of temperature ﬂuctuations is governed by the ther-

mal diﬀusivity a. Pressure ﬂuctuations in ﬂuids are moving with sound speed

and their decay is governed by the sound attenuation D

. In a binary ﬂuid

mixture the decay of concentration ﬂuctuations is governed by the mutual

diﬀusion coeﬃcient. Altogether, these ﬂuctuations result in a characteristic

spectrum of the scattered light [7] which is shown schematically in Fig. 15.2.

The temperature and/or concentration ﬂuctuations contribute to the cen-

tral or frequency-unshifted Rayleigh component of the spectrum of the scat-

tered light. The pressure ﬂuctuations cause the Brillouin lines which are

shifted by ω

relative to the frequency ω

of the incident light. The widths

of these three lines, which in good approximation all exhibit a Lorentzian

form, yield information on the relaxation of the ﬂuctuations in the ﬂuid and

thus on the transport properties. In particular, the widths of the Brillouin

lines are governed by the attenuation of sound D

, the width of the Rayleigh

line is determined by the thermal diﬀusivity a, and, in case of a binary ﬂuid

mixture, also by the mutual diﬀusion coeﬃcient D

. Additionally, the fre-

582 Alfred Leipertz and Andreas P. Fr¨oba

quency spacing ω

between the Rayleigh and Brillouin lines is proportional

to the speed of sound c

, and the ratio of the intensities of the Rayleigh and

the Brillouin lines results in the Landau-Placzek ratio S = I

/(2I

), which

contains information on the speciﬁc heats, c

and c

, at constant pressure

and constant volume, respectively. When adding spherical particles to the

ﬂuid, the width of the Rayleigh line is governed by the particle diﬀusion

coeﬃcient D

, which is related to the particle diameter and the dynamic

viscosity. Thus, several diﬀerent thermophysical properties of interest can be

determined nearly simultaneously by analysing the spectrum of the scattered

light.

15.2.2 Correlation Technique

The use of classical interference spectroscopy (Fabry-Perot spectroscopy)

seems to be the straightforward way to analyse the Rayleigh-Brillouin triplet.

This ﬁltering scheme is, however, only possible under special conditions, for

instance in the transition region from the kinetic to the hydrodynamic regime

where the Rayleigh line is relatively broad [9, 10]. Usually, the width of the

Rayleigh lines of order MHz or below for most cases of practical interest is

such small that it is far beyond the resolving power of Fabry-Perot interferom-

eters. This is the reason for analysing the spectrum of the scattered light in a

post-detection ﬁltering scheme where the total intensity is ﬁrst detected and

the detector signal is later ﬁltered and processed. In this type of detection

one measures optionally the second-order power spectrum of the scattered

light or, as is described in some detail in the following, the time-dependent

intensity correlation function which also is named second-order correlation

function

(2)

(τ) ≡I(0)I(τ) = lim

T →∞



−T

I(t)I(t + τ)dt. (15.3)

The brackets indicate the time average of the product I(t)I(t + τ ). The

spectral range has an upper limit of about 20 MHz corresponding to the time

resolution of the correlator instrument.

In general, the time correlation function gives information on the degree

to which two dynamical properties are correlated over a considered period of

time. In the following we ﬁrst discuss some of the basic properties of these

functions which are relevant to our understanding of light-scattering spec-

troscopy. The time-dependence of the intensity I(t) will generally resemble

a noise pattern. The noise signal in Fig. 15.3 shows that the intensity at the

two times t and t + τ can in general have diﬀerent values. However, when

τ is very small compared to the period of the ﬂuctuations in the intensity,

I(t + τ ) will be very close to I(t) and thus both values are correlated. If τ

increases, I(t + τ)andI(t) become more and more diﬀerent. The correlation

between both values is lost if τ becomes large compared to times typify-

ing the ﬂuctuations in the intensity. A measure of this correlation is the

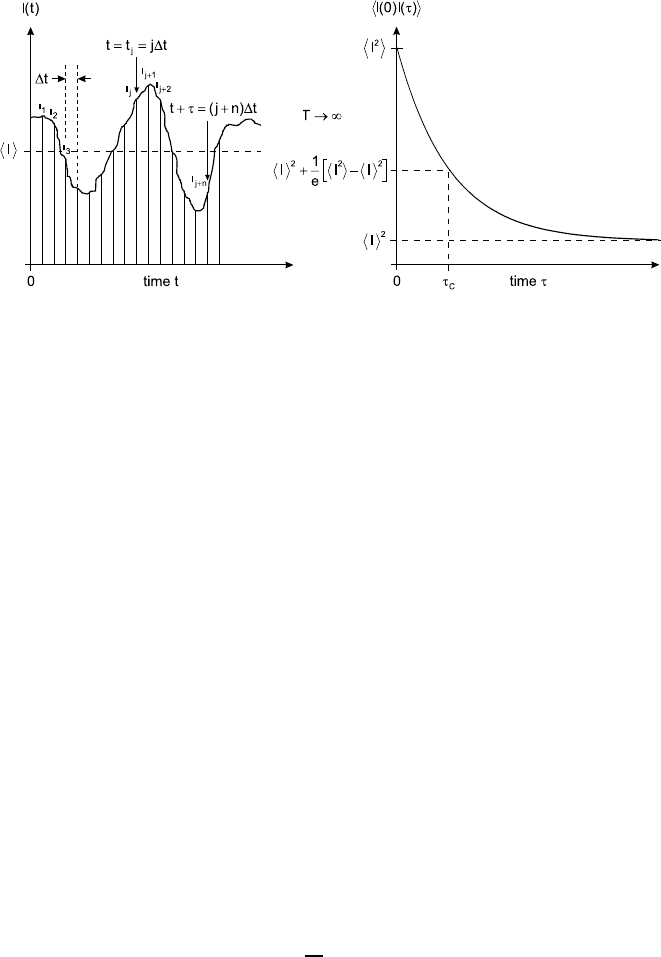
15 Diﬀusion Measurements in Fluids by Dynamic Light Scattering 583

Fig. 15.3. Time-dependence of the intensity I(t) (left) and its time-correlation

function I(0)I(τ ) (right).

correlation function or strictly speaking the autocorrelation function (ACF),

which is deﬁned by (15.3). Here, it is assumed that the inﬁnite time average

(T →∞) of the intensity is independent of its starting value. Such a prop-

erty is called a stationary property. In the case of non-periodic ﬂuctuations

of a stationary property the correlation function starts from its initial value

I

 = I(0)I(0) which is a maximum and decays to I

= I(0)I(τ) as

I(t+ τ)andI(t) become statistically independent for long times τ →∞.The

exact form of the correlation function depends on the underlying scattering

process and on the experimental conditions which is discussed in more detail

later in this chapter. In many applications the correlation function decays

like a single exponential. Here the decay time τ

is the time for which the

time-dependent part of the correlation function has decayed to the fraction

1/e of its initial value. The decay time τ

reﬂects the mean decay behavior

or life-time of the ﬂuctuations of a particular property. This is characteristic

for the decorrelation of signals.

In a realistic experimental situation, besides the light scattered from the

ﬂuctuations in a sample, also contributions from stray light, e.g., from dust on

the cell windows or from the cell windows themselves, may occur. Therefore,

for a general description, we consider a local oscillator ﬁeld coherent with the

incident electric ﬁeld. In terms of the total electric ﬁeld E(t)=E

(t)+E

(t),

which represents a superposition of the scattered electric ﬁeld E

(t)withthe

local oscillator ﬁeld E

(t), the intensity or, more precisely, the radiative ﬂux

I(t)=

c

∗

(t)E(t), (15.4)

measured by a detector, is given by

584 Alfred Leipertz and Andreas P. Fr¨oba

I(t)=

c



(t)+E

(t)



= I

(t)+I

(t)+

c



∗

(t)E

(t)+E

∗

(t)E

(t)



(15.5)

where the asterisk denotes the complex conjugate variable, c the speed of

light, and  the permittivity of the medium. In the following the time de-

pendence of the electric ﬁeld of the incident light at a ﬁxed space point will

be considered more precisely by E

(t)=E

exp [−iω

t +iΨ(t)], where Ψ(t)is

a slowly varying random function representing ﬂuctuations in the phase of

the incident light. The characteristic time behavior of the ﬂuctuations in the

phase is determined by the inverse linewidth of the incident light. Further-

more, the scattered electric ﬁeld can be written in the form E

(t)=f(t)E

(t),

where f(t) is a stochastic complex quantity being proportional to the ﬂuctu-

ations in the electric susceptibility

f(t) ∝ ∆χ

(t)=

⎧

⎪

⎩

∂χ

∂H

⎫

⎪

⎭

∆H

(t), (15.6)

with ∆χ

(t)and∆H

(t) being the Fourier amplitudes of ∆χ

(r,t)and

∆H(r,t) of a ﬂuctuation with wave vector q, respectively [11]. Here, H

may be identiﬁed with the temperature (or entropy), pressure, and species

concentration in ﬂuid mixtures. For a general description also the electric

ﬁeld of a local oscillator will be considered in terms of the incident ﬁeld by

(t)=f

(t) with a constant strength f

. In calculating (15.3) one

obtains from the product I(t)I(t + τ) sixteen terms, whereby as a result of

taking the time average only the six terms

(t)I

(t + τ)+I

(t)I

(t + τ)+I

(t)I

(t + τ)+I

(t)I

(t + τ)





∗

(t)E

∗

(t + τ)E

(t + τ)+c.c.



(15.7)

show a non-vanishing contribution to the intensity correlation function. The

abbreviation c.c. stands for complex conjugate. In taking the time average

of (15.7) the ﬁrst term I

(t)I

(t + τ) corresponds to the intensity correlation

function of the scattered light,

(2)

(τ)=I

(0)I

(τ) =



E

∗

(0)E

∗

(τ)E

(τ), (15.8)

where a local oscillator is absent. For a Gaussian ﬁeld, which is characterized

in a way that at a point of observation many individual components add

to the electric ﬁeld and that the phase functions of these contributions are

equally distributed and mutually independent, the Siegert relation [8]

(2)

(τ)=







(1)

(0)



(1)

(τ)





, (15.9)

15 Diﬀusion Measurements in Fluids by Dynamic Light Scattering 585

holds, which connects G

(2)

(τ) with the ﬁeld correlation function (ﬁrst-order

correlation function)

(1)

(τ) ≡E

∗

(0)E

(τ) = lim

T →∞



−T

∗

(t)E

(t + τ)dt. (15.10)

The optical or ﬁrst-order power spectrum S

(ω) accessible by classical inter-

ference spectroscopy is, according to the Wiener-Khintchine theorem, directly

connected with G

(1)

(τ) by a Fourier transform

(ω)=

2π



+∞

−∞

(1)

(τ)exp(iωτ)dτ. (15.11)

Substituting the above stated expressions for the electric ﬁeld of the incident

and scattered light E

(t)andE

(t), respectively, into (15.10) one obtains for

the ﬁrst-order correlation function

(1)

(τ)=|E

exp [−iΨ(0) + iΨ (τ)]f

∗

(0)f(τ)exp (−iω

τ), (15.12)

where the correlation functions of f (t)andexp[iΨ(τ)] are separated since the

laser source and the medium can be considered statistically independent of

each other. As can be seen from (15.12), the optical power spectrum, which

is the Fourier transform of G

(1)

(τ), see (15.11), is in part determined by the

phase ﬂuctuations of the incident light. Thus, a further limiting factor of clas-

sical interference spectroscopy is obvious. If the spectral width of the incident

light is larger than the width of the spectrum governed by the microscopic

ﬂuctuations in the electric susceptibility, the ﬁeld correlation function of the

scattered light and hence the optical power spectrum is dominated by the

phase ﬂuctuations of the incident light. In contrast, the phase ﬂuctuations of

the incident light cancel out in the second order power spectrum or in the

corresponding intensity correlation function of the scattered light

(2)

(τ)=I

+ I

|f

∗

(0)f(τ)|

f

∗

(0)f(0)

−2

, (15.13)

which is obtained by substituting (15.12) into the Siegert relation (15.9). In

deriving (15.13) it has been assumed that only one individual component

dominates the spectrum of the scattered light. This is equivalent to say that

only ﬂuctuations in one property H of the medium cause ﬂuctuations in its

electric susceptibility. In (15.13) I

denotes the time average of the scattering

intensity

c

f

∗

(0)f(0), (15.14)

originated by the ﬂuctuations in the quantity H. With the help of (15.13)

and (15.14) and taking into account that there is no interaction between

the intensity of the local oscillator and the intensity of the scattered light,

one obtains by taking the time average of (15.7) for the intensity correlation

function in the presence of a local oscillator ﬁeld

586 Alfred Leipertz and Andreas P. Fr¨oba

(2)

(τ)=(I

+ I

)

+ I

|f

∗

(0)f(τ)|

f

∗

(0)f(0)

−2

+2I

f

∗

(0)f(τ)f

∗

(0)f(0)

−1

(15.15)

where the time average of the intensity of the local oscillator is given by

c

. (15.16)

Since the stochastic function f (t) is proportional to the ﬂuctuations ∆H

(t),

see (15.5), with the help of their normalized time correlation function,

(τ)=∆H

∗

(0)∆H

(τ)∆H

∗

(0)∆H

(0)

−1

, (15.17)

(15.15) can be rewritten by

(2)

(τ)=(I

+ I

)

+ I

(τ)|

+2I

(τ). (15.18)

Thus it appears that the intensity correlation function accessible in light scat-

tering experiments gives access to the correlation function of the ﬂuctuations.

In the case of a ﬂuid in the hydrodynamic regime where the mean free path

length r

of the molecules is much smaller than the reciprocal value 1/q of

the modulus of the scattering vector (qr

 1) and by this Onsager regres-

sion hypothesis holds, the time correlation functions of the ﬂuctuations in

the thermophysical properties of state can be derived on the basis of classical

hydrodynamics. Because the ﬂuctuations around the equilibrium values of

temperature (or entropy), pressure, and in addition of species concentration

in ﬂuid mixtures are expected to be very small, the set of the linearized equa-

tions of ﬂuid mechanics can be used. For the hydrodynamic modes of a ﬂuid

the correlation functions g

(τ) can be found ultimately from the linearized

hydrodynamic equations by applying a Fourier-Laplace analysis [7]. As for

many other non-periodic statistical processes, such as for the diﬀusion of par-

ticles in dispersions, also for the statistical ﬂuctuations of temperature (or

entropy) and species concentration in a ﬂuid mixture, the normalized time

correlation function decays like a single exponential,

(τ)=exp(−τ/τ

), (15.19)

where τ

=(Dq

)

−1

is called the “relaxation time” or the correlation time

of the property. Here, D may be identiﬁed to be the thermal diﬀusivity a,

the mutual diﬀusion coeﬃcient D

or the particle diﬀusion coeﬃcient D

respectively. For the local pressure ﬂuctuations at constant entropy, which

can be represented, to a good approximation, by propagating sound waves,

the normalized time correlation function has the form

(τ)=cos(ω

τ)exp(−τ/τ

), (15.20)

where the correlation time τ

=(D

)

−1

is related to the sound attenuation

. In addition, the frequency ω

= c

q, which is identical with the frequency

15 Diﬀusion Measurements in Fluids by Dynamic Light Scattering 587

of the sound waves observed, gives information about the sound velocity.

Actually, even the correlation function g

(τ) of a pure ﬂuid does not consist

of a simple exponential or damped oscillation, as the ﬂuctuations in pressure

and temperature are present simultaneously. The situation complicates, when

ﬂuid mixtures or particle dispersions are considered. However, as decay times

and/or signal amplitudes are vastly diﬀerent in many experimental situations,

the ACF in a time interval of interest may often be analysed in terms of a

simple exponential. This point will be described in more detail in the following

sections.

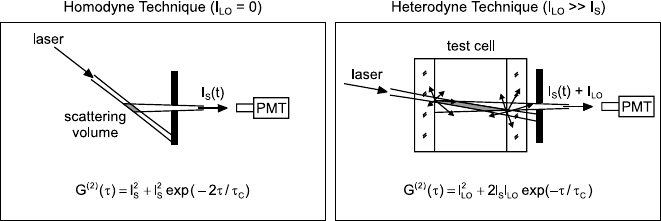
15.2.3 Homodyne and Heterodyne Techniques

As can be seen from (15.18) in the presence of a local oscillator ﬁeld the

correlation function consists of three terms, the constant term (I

+ I

)

the term I

(τ)|

, which is due to the scattered light alone and is denoted

as homodyne term, and the heterodyne term 2I

(τ). In the case that

the correlation function of the hydrodynamic ﬂuctuations g

(τ) decays like

a single exponential we obtain two exponential functions with decay times

being diﬀerent by a factor of two added to a constant background

(2)

(τ)=(I

+ I

)

+ I

exp (−2τ/τ

)+2I

exp (τ/τ

). (15.21)

As it is very diﬃcult to extract reliable information from a sum of two ex-

ponentials with decay times of the same order of magnitude, the aim of the

experimenter is to meet a situation where one of the exponentials clearly

dominates. Either, one has to design the experiment (see Fig. 15.4) in a way

that only light from the sample itself is collected by the detector, I

 I

In this homodyne case, which may be the easier realized the larger the scat-

tering cross section of the ﬂuctuations is, the normalized intensity correlation

function takes the form

(2)

(τ)=1+exp(−2τ/τ

). (15.22)

Fig. 15.4. Homodyne and heterodyne detection scheme.

588 Alfred Leipertz and Andreas P. Fr¨oba

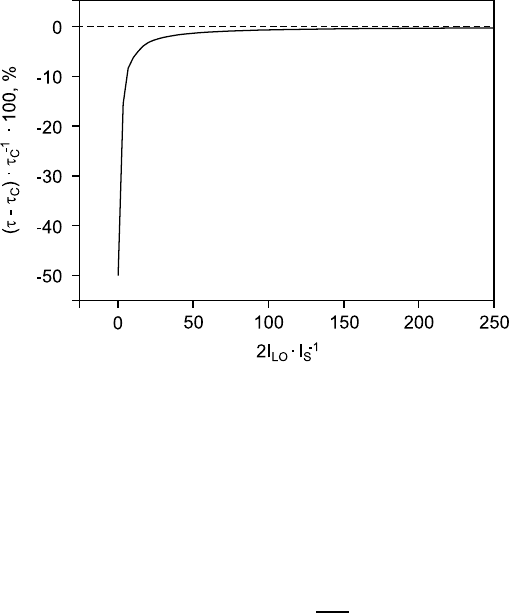
Fig. 15.5. Error in the decay time τ

for a heterodyne experiment introduced if

the ratio 2I

of local oscillator to scattered light signals is not chosen large

enough.

Alternatively, the strict heterodyne case is achieved. This will be done, if

the signal is comparatively weak, and may be accomplished by deliberately

adding some part of the incident beam to the detected signal in a way that

 I

. Now the normalized intensity correlation function has the form

(2)

(τ)=1+

exp (−τ/τ

). (15.23)

It is crucial, however, in either case to make sure that one contribution

clearly dominates. If not, there may be a considerable error, see Fig. 15.5, as

the decay time determined from a ﬁt to a supposed single exponential may

be anywhere in between the two cases. As can be seen from Fig. 15.5 it is

possible to achieve high accuracy in τ

by simply adding enough reference

light I

to the signal I

in the heterodyne technique. A similar solution is

not given for the homodyne technique.

The derivation of (15.22) and (15.23), however, makes implicitly use of

two idealizing assumptions, which in general do not hold. One simpliﬁcation

is that the scattered light is detected at a point in the far ﬁeld. In practice,

both the scattering volume and the area of detection are ﬁnite, which results

in a deviation from an ideal coherent detection. Thus, there is an averaging

eﬀect with a reduction of the contrast b = g

(2)

(0) − 1 as compared to the

value for a perfect registration. The deviation of b from 1 or 2I

in the

case of a homodyne or heterodyne detection scheme, respectively, also takes

into account eﬀects of a ﬁnite speed of signal processing. Another simpliﬁ-

cation is the assumption of a constant intensity of the incident light. Slow

ﬂuctuations in the light source result in a deviation of the baseline from the

15 Diﬀusion Measurements in Fluids by Dynamic Light Scattering 589

ideal value 1 for the correlation function. Here, another adjustable parameter

a is introduced in practice. Thus, a practical ACF takes the form

(2)

(τ)=a + b exp (−2τ/τ

). (15.24)

(2)

(τ)=a + b exp (−τ/τ

). (15.25)

assuming homodyne or heterodyne conditions, respectively.

The application of the heterodyne technique is advantageous for achieving

high accuracy in the determination of τ

, see Fig. 15.5, and is especially useful

for the evaluation of the periodic pressure ﬂuctuations at constant entropy,

which are responsible for the Brillouin components of the spectrum. In the

case of a pure ﬂuid a usual homodyne intensity ACF exhibits terms due to

both pressure and temperature (or entropy) ﬂuctuations and an additional

cross term. To analyze the pressure ﬂuctuations in a heterodyne detection

scheme, the frequency of the local oscillator is shifted relative to the fre-

quency ω

of the laser light by ω

applying an acousto-optical modulator.

The frequency shift ω

is of the same order of magnitude as the frequency ω

of the pressure ﬂuctuations observed (ω

≈ ω

). By a proper choice of the

intensity of the local oscillator shifted in frequency the signal governed by the

periodic pressure ﬂuctuations may be strongly enhanced as compared to that

of the temperature (or entropy) ﬂuctuations, and the correlation function

takes the form of a damped oscillation

(2)

(τ)=a + b cos (∆ωτ)exp(−τ/τ

). (15.26)

Now the speed of sound c

can be found from the knowledge of the adjusted

modulator frequency ω

and the residual detuning ∆ω = |ω

− ω

| of the

correlation function according to c

= ω

/q =(ω

± ∆ω)/q. As mentioned

above, the sound attenuation D

can be determined from the correlation time

=(D

)

−1

15.3 The Dynamic Light Scattering Experiment

15.3.1 Setup

In this section some fundamentals of the design of a light scattering appara-

tus are discussed. The exact choice of the individual components naturally

depends strongly on the exact goal of the experiments, i. e., which property is

to be measured. A possible setup is displayed schematically in Fig. 15.6. The

main portion of the laser light is irradiated into a thermostated sample cell,

beam splitters allow one to add some reference light for a heterodyne detec-

tion, the frequency of which may be shifted for measurements on the Brillouin

lines. Part of the scattered light is imaged, in the simplest case only by means