Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

600 Alfred Leipertz and Andreas P. Fr¨oba

15.4.2 Mutual Diﬀusion Coeﬃcient

The problems encountered in measuring the mutual diﬀusion coeﬃcient D

are of a similar nature as those of measuring the thermal diﬀusivity of mix-

tures. In either case there are basically signals from both temperature and

concentration ﬂuctuations. As the mutual diﬀusion coeﬃcient is in general

at least one order of magnitude smaller than the thermal diﬀusivity, larger

angles may be chosen for the determination of this property. It is especially

interesting, however, to perform the measurements with an identical setup

as for a, as both properties may then be measured simultaneously. Whether

one succeeds, is again governed by the actual separation of decay times and

by the ratio of the signals.

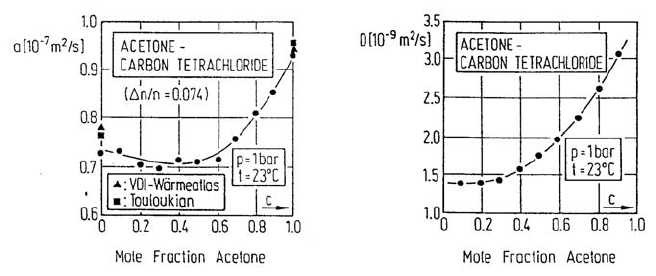
As an example, the thermal diﬀusivity and the mutual diﬀusion coeﬃcient

of the binary system acetone and carbontetrachloride with a diﬀerence in the

refractive indices of 7.4% are shown in Fig. 15.13, where the situation is

favourable, as the signals are of the same order of magnitude [32].

In most instances, especially when the diﬀerence of refractive indices

is large, the determination of the mutual diﬀusion coeﬃcient may be per-

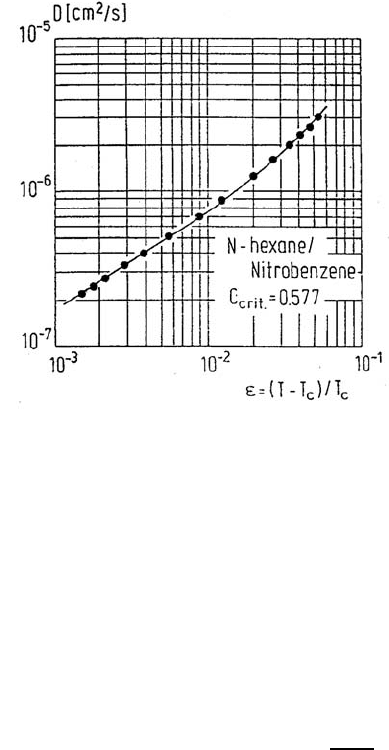
formed by standard experiments. Fig. 15.14 shows the measured tempera-

ture dependence of the mutual diﬀusion coeﬃcient of the separation system

n-hexane/nitrobenzene [33]. According to the stability theory of thermody-

namics, D

disappears at the critical separation point (temperature T

which can be clearly seen from Fig. 15.14. This eﬀect of vanishing diﬀusiv-

ities on approaching the critical point is generally referred to as “critical

slowing down”. Further details about the theory of mutual diﬀusion includ-

ing the phenomenon of the critical slowing down may be found in Chaps. 3

14, and 16 (Fig. 16.29).

Fig. 15.13. Thermal diﬀusivity and mutual diﬀusion coeﬃcient of the mixture

acetone/carbon tetrachloride as a function of composition [32].

15 Diﬀusion Measurements in Fluids by Dynamic Light Scattering 601

Fig. 15.14. Mutual diﬀusion coeﬃcient of a separation system as a function of the

reduced temperature  =(T − T

)/T

[33].

15.4.3 Dynamic Viscosity

The determination of the dynamic viscosity η of liquids is in some way diﬀer-

ent from the measurement of the other properties treated so far, as it requires

the addition of seed particles. The quantity which is actually measured is the

(translational) particle diﬀusion coeﬃcient D

of spherical particles, which

results in another Rayleigh peak in the spectrum. The particle diﬀusion co-

eﬃcient is related via the Stokes-Einstein equation [34,35]

3πηd

(15.31)

with viscosity η, particle diameter d, Boltzmann constant k

and tempera-

ture T . In the low-concentration range (i.e. under the assumption that there

is no particle-particle interaction as implied in fact for deriving (15.31)) this

diﬀusivity is clearly nothing else than the particle self-diﬀusivity (cf., e.g.,

Chaps. 10, 14, and 16). Two possible ﬁelds of applications are contained in

this relation. One area of research is the determination of particle size dis-

tributions and, as macromolecules may be regarded as special particles, the

determination of molecular weight [36,37]. As with a distribution of particle

sizes a distribution of particle diﬀusion coeﬃcients results, the ACF is a su-

perposition of exponentials with various decay times. The major problem in

this ﬁeld is then to recover the size distribution from the experimental ACF,

which is a diﬃcult and, with experimental noise given, sometimes impossi-

602 Alfred Leipertz and Andreas P. Fr¨oba

Fig. 15.15. Electron microscope picture of silica particles, courtesy: A.P. Philipse,

University of Utrecht.

ble task, as diﬀerent size distributions may result in very similar correlation

functions. Here, the other application related with particle diﬀusion coeﬃ-

cients shall be given some more consideration, namely the determination of

the dynamic viscosity [38–40].

Generally, as D

is orders of magnitude smaller than the other diﬀu-

sion coeﬃcients in the Rayleigh-Brillouin spectrum, this quantity is normally

probed at large scattering angles. Another diﬀerence is that for the determi-

nation of the viscosity the usage of low-power lasers such as He-Ne or diode

lasers is suﬃcient in most cases, as the scattering cross section of the parti-

cles is usually much larger than that of other ﬂuctuations in the ﬂuid itself.

Accordingly, a homodyne detection scheme is normally employed, and the

measurements are not aﬀected by other components in the spectrum.

A key to a successful determination of the viscosity is the choice of suit-

able particles in a size range of some 20 nm to 500 nm. These are to be

spherical and monodisperse, or at least are to exhibit a narrow size distribu-

tion, in order to ensure a correlation function which matches the model of a

pure exponential, which is essential for a reliable data evaluation. Moreover,

they must be chemically stable and form stable dispersions. There have been

a number of investigations with diﬀerent seed particles, but it has turned out

that silica particles with various surface modiﬁcations are most appropriate

for a wide range of liquids (see Fig. 15.15). Particle sizes are best calibrated

by DLS measurements in liquids with known viscosities. For high-accuracy

measurements the governing conditions of the working model must be met

what means in this case unhindered particle diﬀusion and no multiple scatter-

ing in the sample. For these reasons it is essential to use low particle volume

fractions of typically 10

−4

and to vary the particle concentration and/or scat-

tering angle. In connection with a careful inspection of the ACF this approach

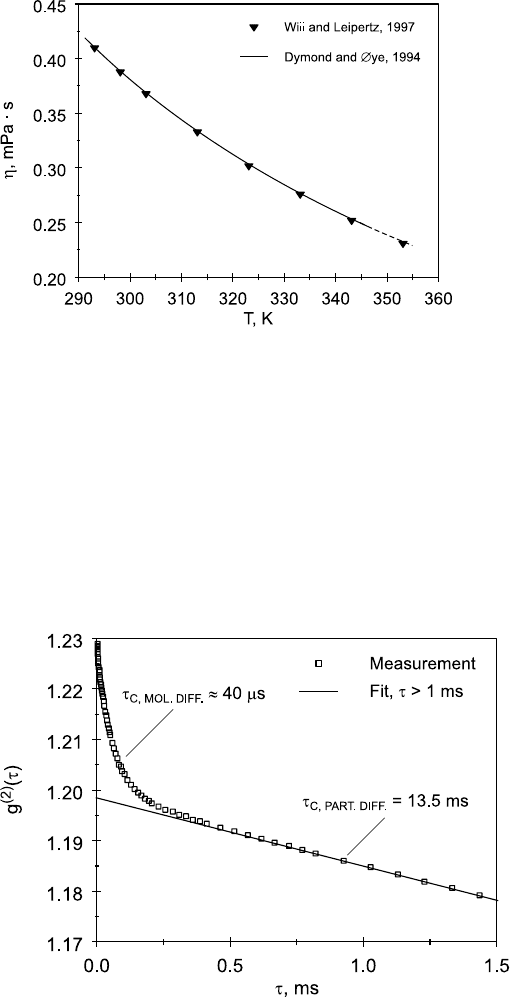
ensures reliable results. An experimental result is shown in Fig. 15.16, where

the viscosity of n-heptane was measured to check the technique. This liquid

was chosen, because there are reliable reference data [41] both for n-heptane

15 Diﬀusion Measurements in Fluids by Dynamic Light Scattering 603

Fig. 15.16. Viscosity of liquid n-heptane [40] in comparison with reference data

[41].

itself and for n-hexane and n-octane, which were used for calibrating the

particle size at room temperature.

As the numerical value of the mutual diﬀusion coeﬃcient is in between

those of the thermal diﬀusivity and the particle diﬀusion coeﬃcient, prospects

open of a simultaneous measurement of η and D

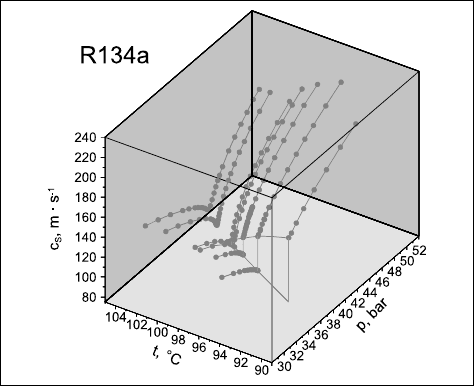
. In Fig. 15.17 a correlation

function is plotted, which was measured in a paraﬃn oil, a mixture of many

hydrocarbons of chain lengths ranging from about 15−40 carbon atoms. Per-

Fig. 15.17. Experimental ACF of a paraﬃn oil with seed particles added. The

signals from particle and molecular diﬀusion may be clearly separated [42].

604 Alfred Leipertz and Andreas P. Fr¨oba

forming a ﬁt for times larger than 1 ms the ACF can be very well represented

by a single exponential with a decay time of 13.5 ms. Additionally, there is

another signal at small decay times, which is due to molecular diﬀusion and,

due to the nature of this multi-component mixture, is built up of several

individual diﬀusion signals.

15.4.4 Sound Velocity and Sound Attenuation

For the measurement of sound velocity c

and sound attenuation D

the

Brillouin components of the spectrum are investigated. As the Brillouin lines

are shifted in frequency, a heterodyne technique with a local oscillator, which

is also shifted in frequency by means of an acousto-optic modulator, is used

[3]. This results in a correlation function in form of a damped oscillation,

(15.26), where the sound attenuation is determined from the decay-time τ

as usual and the sound velocity is deduced from the known frequency shift

by the modulator ω

and the residual mistuning ∆ω of the correlogram.

The simplest way of determining ∆ω is by applying a Fourier transform to

the measured correlation function, where the frequency is found from the

maximum of the resulting spectrum [43]. Dynamic light scattering can be

used to measure the sound velocity with an uncertainty of about 0.5%. This

technique has again been often applied to various refrigerants [29, 44]. An

example is depicted in Fig. 15.18.

In determining the sound attenuation one has to face two problems. One

is that due to the large width of the Brillouin lines the decay-time of the

Fig. 15.18. Sound velocity of refrigerant R134a in a wide range around the critical

point [46].

15 Diﬀusion Measurements in Fluids by Dynamic Light Scattering 605

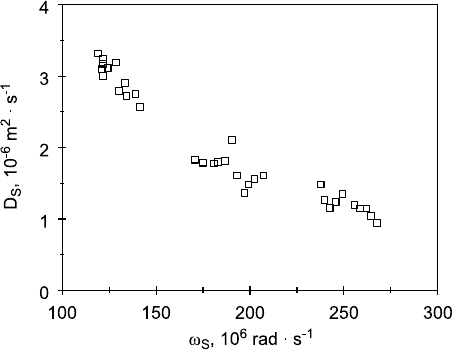
Fig. 15.19. Frequency dispersion with the measurement of sound attenuation;

sample: refrigerant R125, saturated liquid at 45

◦

C [44].

correlation function is typically only a few hundreds of nanoseconds, even if

small scattering angles are employed, which requires the use of fast correla-

tors. The other problem is of a more fundamental nature and is caused by a

lack of deﬁnition of the scattering vector [3, 44]. Due to the ﬁnite width of

stops in the detection optics there is always some angular spread, which is a

combination of a simple geometrical and a diﬀraction eﬀect. This uncertainty

does not have a signiﬁcant eﬀect on probing the Rayleigh line, but causes a

spread in the position of the Brillouin line. Thus, the linewidth probed in a

spectroscopic experiment is a convolution of the distribution of positions and

the actual linewidth. Analyzing the scattered light in the time-domain one

obtains in the presence of this eﬀect a decay time being shorter than asso-

ciated with the sound attenuation. However, one has to realize experimental

conditions, where the angular uncertainty is as small as possible. This may

be realized by placing the stops in the detection optics as far as 4 −6 m apart

from each other.

These diﬃculties result in a reduced accuracy of measuring D

of about

10%, which still is better than by direct spectroscopic methods. Finally, it

must be pointed out that all measurements of sound velocity and attenuation

are basically dependent on the actual frequency used in the experiment. This

dispersion eﬀect has turned out to be negligible for many ﬂuids and the

frequencies probed by DLS as the sound velocity is considered, but is marked

for the sound attenuation, especially of refrigerants, cf. Fig. 15.19.

606 Alfred Leipertz and Andreas P. Fr¨oba

15.4.5 Landau-Placzek Ratio

The Landau-Placzek ratio S is deﬁned as the ratio of intensities of the

Rayleigh to Brillouin lines and is related to the speciﬁc heats c

and c

S =

− c

)

. (15.32)

The Landau-Placzek ratio may be obtained from the evaluation of the con-

trasts in various heterodyne experiments, when a local oscillator with deﬁned

intensity is added [45]. An example of such measurements is provided by

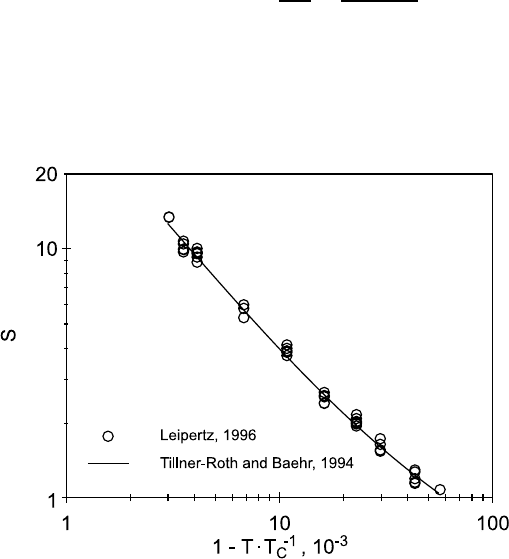
Fig. 15.20.

Fig. 15.20. Landau-Placzek ratio for refrigerant R134a obtained by DLS measure-

ments [47] in comparison with reference data from the equation of state [48].

15.4.6 Soret Coeﬃcient

When a binary liquid mixture is brought into a temperature gradient ∇T ,

mass diﬀusion occurs resulting in a concentration gradient ∇c.ThisSoret

eﬀect may be described by the relation

∇c = −S

c(1 − c) ∇T, (15.33)

where S

is the Soret coeﬃcient and c is the mass fraction of the heavier

component. When DLS experiments are carried out in a steady temperature

15 Diﬀusion Measurements in Fluids by Dynamic Light Scattering 607

gradient, the Soret coeﬃcient may be derived from the amplitude of the con-

centration mode in the resulting correlation function [49]. As this amplitude

is proportional to (∇T )

very small scattering angles of order 1

◦

must be

employed, where the scattering angle can hardly be measured exactly, but

may be calibrated by a DLS measurement in a system where the diﬀusion

coeﬃcient is known.

15.4.7 Derivable Properties

Dynamic light scattering is a technique which allows the measurement of a

large variety of thermophysical properties, in some instances even within a

single experiment. Besides the data, which can be measured directly, more

properties may be derived in connection of DLS data with additional infor-

mation from other techniques. A few examples will be given here.

Whereas the Landau-Placzek ratio relating isobaric and isochoric speciﬁc

heat capacities, (15.32), may be directly derived from DLS experiments, there

is no straightforward access to either of these values. In order to obtain in-

formation on c

, it is therefore necessary to combine data from DLS with

other properties from diﬀerent measurement techniques. As DLS can probe

the thermal diﬀusivity very successfully, the combination with data for the

thermal conductivity λ, which can be measured by various techniques di-

rectly, and for the ﬂuid density ρ, which can be determined very accurately,

yields information on c

according to c

= λ/(aρ). An example for this proce-

dure including a comparison with values obtained from an equation of state

is given by Fr¨oba et al. [50]. Using c

and S, the isochoric heat results as

= c

/(S + 1) which immediately follows from (15.32).

The isentropic compressibility χ

=1/(ρc

) follows directly from density

ρ and the sound velocity c

measured by DLS. Accordingly, the isentropic

exponent κ = ρc

/p may be derived with the knowledge of the equation of

state of the ﬂuid. The sound attenuation D

is related to a number of other

thermophysical properties via

(4/3)η

+ η

+(1/c

− 1/c

)λ

2ρ

. (15.34)

In this notation, the usual dynamic viscosity has been given an index s to

emphasize that this is the shear viscosity in contrast to the bulk viscos-

ity η

.WithameasurementofD

and knowledge of the other quantities,

which again may mostly be derived from DLS measurements, information on

the bulk viscosity may be deduced, which is an important property for the

description of structural relaxation and which is not readily obtainable by

experiment.

608 Alfred Leipertz and Andreas P. Fr¨oba

15.5 Related Techniques

15.5.1 Surface Light Scattering

Surface light scattering (SLS) is a technique which is closely related to dy-

namic light scattering in its classical meaning. The diﬀerence is that this

technique probes, as the name indicates, ﬂuctuations on the surface of a liq-

uid or, in a more general formulation, at phase boundaries. These ﬂuctuations

can be understood as thermally excited capillary waves of small amplitude

(∼ 1 −100 nm) and with a characteristic wavelength (∼ 0.1 −1000 µm) and

that are quantized in so-called “ripplons” [51].

In general, for the temporal decay of surface ﬂuctuations two cases may be

distinguished. In the case of large viscosity and/or small surface tension, the

amplitude of surface waves is damped exponentially, while in the case of small

viscosity and/or large surface tension the amplitude decays in the form of a

damped oscillation. Light interacting with such a ﬂuctuating surface structure

is scattered. An exponential decay of surface waves results solely in a spectral

broadening of the light spectrum, whereas an oscillatory damping gives rise

to a Brillouin doublet [52]. Hence, the spectrum exhibits three characteristic

lines, qualitatively similar to that from light scattered in a bulk ﬂuid, where

line widths and separation are related to the modulus q of the scattering

vector, kinematic viscosity ν, surface tension σ, and density ρ as shown in

Fig. 15.21 in a ﬁrst order approximation. A Lorentzian shape of these lines as

well as the relations for line widths and separation as indicated in Fig. 15.21

only hold in the limiting cases y  0.145 or y  0.145, respectively, with

Fig. 15.21. Spectrum of scattered light by surface waves: frequency unshifted line

(center) in the case of large viscosity and/or small surface tension; frequency shifted

Brillouin lines in the case of small viscosity and/or large surface tension.

15 Diﬀusion Measurements in Fluids by Dynamic Light Scattering 609

y = σρ/(4η

q). For y values close to 0.145 the line shapes become more

complex [51,53].

In practice, also the spectrum of light scattered by the ﬂuctuations at a

liquid surface can only be resolved in a post-detection ﬁltering scheme us-

ing, e.g., photon correlation spectroscopy (PCS). For heterodyne conditions,

where the scattered light is superimposed with stronger coherent reference

light, the normalized time-dependent intensity correlation function for the

analysis of surface ﬂuctuations is described by

(2)

(τ)=a + b cos (ω

τ)exp(−τ/τ

). (15.35)

(2)

(τ)=a + b exp (−τ/τ

). (15.36)

assuming the decay of the amplitude of surface waves is oscillatory (y 

0.145) or overdamped (y  0.145), respectively. Due to the usually small

frequency separation of the shifted Brillouin lines commonly no frequency

shift of the coherent reference light is necessary. In the propagating case

of surface ﬂuctuations the correlation function (15.35) can be used for the

simultaneous evaluation of surface tension σ and kinematic viscosity ν.The

correlation time τ

and the frequency ω

, which are identical with the mean

life time of “ripplons” and the frequency of propagation, respectively, are

given in ﬁrst order approximation by

2νq





1/2

3/2

. (15.37)

In the overdamped case, if the ﬂuid viscosity is large and/or the surface

tension is very small, the lifetime of “ripplons” in (15.36) is given in a ﬁrst-

order approximation by

2νρ

σq

. (15.38)

For a reliable determination of viscosity and surface tension a more detailed

and rigorous consideration of the surface light scattering method than given

by (15.35) to (15.38) has to be applied. Here, the reader is referred to litera-

ture, see, e.g., [54].

Although it has been shown that SLS may be performed in complete anal-

ogy to DLS measurements from bulk ﬂuids using an identical set-up [50,55],

some diﬀering design features are often employed for SLS measurements. One

obvious diﬀerence is that SLS normally investigates interfaces in horizontal

orientation within a sample cell with light impinging from above. Commonly,

scattered light is observed near the reﬂected beam [56], i.e. also in the top

direction, which eases the optical access and is of course essential for non-

transparent ﬂuids. Alternatively, for transparent ﬂuids scattered light may

be observed close to the direction of the refracted beam [57, 58], which is

advantageous due to stability considerations and scattering intensities. By