Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

630 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

W (t) ∼ t

,t τ

. (16.30)

For times large as compared to the momentum relaxation time τ

, when the

sphere has experienced many collisions with solvent molecules, the MSD has

changed into a linear function of time, i.e.

W (t)=D

t, t τ

, (16.31)

where D

is referred to as the single particle or Stokes-Einstein diﬀusion

coeﬃcient.

Thetimescaleτ

can be inferred from the following reasoning originally

due to Langevin. A sphere with velocity v experiences through the solvent

impacts an average friction force that is equal to −γ v,whereγ is referred

to as the friction coeﬃcient, and a ﬂuctuating force f (t). For a sphere, the

friction coeﬃcient γ is given by the Stokes law γ =6πη

R,whereη

is the

shear viscosity of the solvent and R is the radius of the sphere. For times large

as compared with the mean collision time, τ

, of solvent molecules (typically,

≈ 10

−13

s), the colloidal sphere has experienced many collisions by the

solvent molecules. Then the force f (t) can be described as a Gaussian dis-

tributed ﬂuctuating quantity completely characterized by its ﬁrst and second

moments

f(t) =0, f(t) · f (t



) =2dB δ(t − t



) . (16.32)

Here, ···is an average over the fast solvent collisions, and B is a measure of

the strength of the ﬂuctuating force. In thermal equilibrium, B = k

Tγ, i.e.

the strength is proportional to the temperature and friction coeﬃcient. The

delta function in time indicates that, as seen from a coarse-grained time level

t  τ

, there is no correlation between solvent impacts at diﬀerent times.

The Newtonian equation of motion for a Brownian sphere of mass M is

thus given, for times t  τ

,by

= − γ v(t)+ f (t). (16.33)

with the solution

v(t) = v

exp

−

(16.34)

for the solvent-collision-averaged velocity. As seen, the velocity remains on

average almost equal to the initial velocity v

for times t  M/γ,whichsets

thetimescale

≡

6πη

(16.35)

for the average velocity relaxation of a colloidal sphere. For times t  τ

the average velocity of a tagged particle decays towards zero. Using typical

values for aqueous colloidal dispersions, one ﬁnds that τ

≈ 10

−8

− 10

−9

so that τ

 τ

16 Diﬀusion in Colloidal and Polymeric Systems 631

So far we have considered the Brownian motion of a sphere with given

ﬁxed initial velocity v

. In dynamic light scattering experiments, an addi-

tional average is performed with respect to a Maxwellian distribution of ini-

tial particle velocities since light is scattered from many spheres in thermal

equilibrium. Multiplication of (16.33) by v

and subsequent averaging over

solvent collisions and initial velocities gives

(t) ≡

v(t) · v(0) =

exp



−



(16.36)

for the velocity autocorrelation function (VAF), φ

(t), of an isolated Brown-

ian sphere. Due to equipartition of energy at equilibrium, v

(t) = dk

T/M.

Using that r(t) −r



v(t



) one can easily show for stationary systems

that φ

(t) is related to the MSD by

W (t)=



du (t − u) φ

(u) . (16.37)

This relation is valid also for non-dilute system of interacting particles. The

MSD of an isolated sphere follows from the substitution of (16.36) into (16.37)

W (t)=D



1 −



1 − e

−t/τ



→



,τ

 t  τ

t, t  τ

(16.38)

where D

is related to the friction coeﬃcient by the Stokes-Einstein relation

. (16.39)

Equation (16.38) interpolates between random ballistic ﬂight for t  τ

and

linear diﬀusive behavior for t  τ

The sphere displacement ∆r(t) during time t is a Gaussian random vari-

able, since it is linearly related to v(t)andtof(t). The pdf, P (∆r,t), for

such a displacement is thus

P (∆r,t)={4πW(t)}

−d/2

exp{−

(∆r)

4W (t)

} (16.40)

with

W (t)=



P (∆r,t)(∆r)

. (16.41)

The pdf is the solution of the diﬀusion-like equation

∂

∂t

P (∆r,t)=D(t)∇

P (∆r,t) , (16.42)

where

632 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

D(t) ≡

W (t)=D



1 − e

−t/τ

, (16.43)

subject to the initial condition P (∆r,t=0)=δ(∆r). The latter follows from

(16.40) specialized to t = 0. Here, ∇ is the d-dimensional gradient operator.

Knowing the pdf we can calculate from (16.40) the self-dynamic structure

factor

(q, t)=



d(∆r)e

iq·∆r

P (∆r,t)=exp{−q

W (t)}, (16.44)

which, for uncorrelated spheres, depends on time only through W (t). Note

for the dilute dispersions of uncorrelated particles considered here that the

collective dynamic structure factor S

(q, t) reduces to the self-dynamic one.

In typical dynamic light scattering experiments on colloidal suspensions,

times t>10

−6

s  τ

and hence distances large compared to (D

)

1/2

are

resolved. In this so-called diﬀusive regime, (16.42) reduces to the one-particle

diﬀusion equation

∂

∂t

P (∆r,t)=D

∇

P (∆r,t) , (16.45)

which has (16.40) specialized to W (t)=D

t as its fundamental solution.

The diﬀusion (16.45) is statistically equivalent to the overdamped Langevin

equation

v(t)=

f(t) , (16.46)

and f according to (16.32), which expresses a force balance, i.e an inertia-free

sphere motion for times t  τ

In fact, Brownian motion of a colloidal particle is adequately described

by the Langevin equation (16.33) with δ-correlated random force only when

solvent inertia is negligible, i.e. for times t  τ

only, where it reduces to

(16.46). The Langevin equation disregards, for shorter times t ≈ τ

,the

feedback on the particle velocity from the surrounding solvent. The solvent

cannot instantaneously follow the changes in the particle velocity. Through

the retarded response of the solvent, the sphere velocity is inﬂuenced by its

values at earlier times. This leads to an enlarged persistence in the velocity

autocorrelations. These solvent memory eﬀects on the sphere velocity can

be adequately described, for d = 3 by the retarded (one-particle) Langevin

equation

= −



duγ(t − u) v(u)+ f(t) (16.47)

which includes a time-dependent friction function γ(t) obeying a generalized

ﬂuctuation-dissipation relation

f(t) · f (t



) =3k

Tγ(t − t



) . (16.48)

The random force in the retarded Langevin equation is still Gaussian, how-

ever it is now correlated for diﬀerent times, due to cooperative eﬀects of the

16 Diﬀusion in Colloidal and Polymeric Systems 633

ﬂuid motion. The friction function can be calculated, for times t  τ

,using

macroscopic equations of motion for the solvent ﬂow. Substitution of the hy-

drodynamically determined γ(t) into the retarded Langevin equation results

in closed expressions for the MSD and φ

(t). We only quote the asymptotic

forms valid for t  τ

, viz. [6–8]

W (t) ≈ D



1 −

√





1/2



(16.49)

and

(t)=

W (t) ≈

√





−3/2

(16.50)

where τ

= a

/η

=(9/2)(ρ

/ρ

)τ

is the time needed for a viscous shear

wave in the solvent of mass density ρ

to diﬀuse across a particle radius. The

mass density, ρ

, of colloidal particles is close to ρ

,andτ

and τ

are thus

of the same order of magnitude.

The positive feedback of the solvent ﬂow on the sphere velocity implies an

algebraic rather than exponential decay of the VAF. Moreover, the algebraic

approach of the single-particle MSD to its long-time-limiting form W (t)=

t is much slower than prediced by (16.38). The occurrence of an algebraic

decay in an autocorrelation function is generally referred to as a long-time

tail. An algebraic tail proportional to t

−1/2

in W (t) was indeed observed in

dynamic light scattering experiments on very large colloidal spheres (since

∝ a

) through the measurement of S

(q, t) and using (16.44) to infer

W (t) [9]. While the non-retarded Langevin equation does not describe dilute

colloidal dispersions for times t ≈ τ

, it can be applied instead for t ≈ τ

aerosols like dust or smoke particles in air, since for these systems one has

 ρ

and hence τ

 τ

The surrounding solvent molecules exert in addition to a random force

a random torque, f

(t), on the colloidal sphere, which causes a rotational

Brownian motion of its angular velocity ω(t). Neglecting solvent inertia, the

erratic sphere rotation can be described in analogy to translational motion

by a rotational Langevin equation, given for d =3andt  τ

dω

= − γ

ω(t)+ f

(t) , (16.51)

with a stochastic torque of zero mean and δ-correlated covariance

f

(t) · f



) =6k

Tγ

δ(t − t



) . (16.52)

According to this Langevin equation, the solvent-collisions-averaged angular

velocity and the equilibrium angular VAF are, respectively,

ω(t) = ω

exp



−



(16.53)

634 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

and

(t) ≡

ω(t) · ω(0) =

exp



−



(16.54)

with the damping time

. (16.55)

Here, γ

=8πη

is the so-called Stokes-Debye friction coeﬃcient of a freely

rotating sphere, and M

=(2/5)Ma

is the moment of inertia of a homoge-

neous sphere. The damping times for the translational and rotational velocity

are of the same order of magnitude, since τ

=(3/10)τ

When the hydrodynamic solvent-sphere coupling is accounted for through

a time-dependent rotational friction function similar to the translational case,

the exponential decay of the rotational VAF is changed for times t  τ

into

the power-law decay [10, 11]

(t) ≈

√





−5/2

(16.56)

which is one power in t slower than the asymptotic decay of the trans-

lational VAF. Depolarized dynamic light scattering is a convenient experi-

mental tool to measure rotational Brownian motion of optically anisotropic

spheres in the diﬀusive regime t  τ

. As mentioned in Sect. 16.2.1, the

polarizability, α, of an optically anisotropic uniaxial sphere is a tensor

α(

u)=α



u + α

⊥

(1 −

u)=α 1 + β



u −



(16.57)

where α



and α

⊥

are the incremental (relative to the solvent) polarizabilities

parallel and perpendicular to the optical axis of the sphere, with α =(α



2α

⊥

)/3andβ = α



− α

⊥

,and

u(t) is the unit orientation vector pointing

along the optical axis. The orientation vector is related to the angular velocity

of the sphere by ω(t)=

u(t) × (d/dt)

u(t).

In depolarized dynamic light scattering, the polarization of the incident

electric light ﬁeld is chosen perpendicular to the scattering plane spanned

by the incident and detected light beam (i.e.

), and one detects

the in-plane component (i.e.

) of the scattered electric ﬁeld. In this

VH-geometry

· α(

u) ·

= β



2π



1/2

2,1

(

u)+Y

2,−1

(

u)] (16.58)

where Y

2,m

is a second-order spherical harmonic function. Together with

(16.15), this results in the EACF [3]

(q, t) ∝ β

(q, t) S

(t) (16.59)

16 Diﬀusion in Colloidal and Polymeric Systems 635

where we have introduced the rotational self-dynamic correlation function

(r)=4πY

2,−1

(

u(0)) Y

2,1

(

u(t)) = P

(

u(t) ·

u(0)), (16.60)

which includes information on the rotational diﬀusion. The second equality

follows from spatial isotropy, i.e. from the m-independence of S

(t), with P

denoting the second-order Legendre polynomial. In deriving (16.60), it has

been assumed that the rotational motion of a sphere is decoupled from the

translational motion for all t  τ

. While this decoupling is strictly valid for

dilute dispersions of non-interacting spheres, it is an approximation for non-

spherical particles and for concentrated sphere dispersions. Note that β =0

for optically isotropic spheres. Then there is no depolarized scattered light

as long as multiple light scattering is negligibly small.

The function S

(q, t) of non-interacting spheres can be calculated for t 

from the rotational diﬀusion equation (Debye equation)

∂

∂t

P (

u,t)=D

P (

u,t) (16.61)

which determines the pdf P (

u,t) of ﬁnding the sphere with orientation

u at

time t. We have introduced here the diﬀusion coeﬃcient of a single and freely

rotating sphere, related to the rotational friction coeﬃcient by the Einstein-

Debye relation

. (16.62)

The Debye equation is the analogue of the translational diﬀusion equation

(16.45), with

L =

u × ∂/(∂

u) denoting the gradient operator in orientation

space. It describes the random walk of the tip of

u(t) on the unit sphere.

Equation (16.61) has the fundamental solution [3]

P (

u,t|

∞



l=1



m=−l

(

u) Y

l,−m

(

)exp{−l(l +1)D

t} , (16.63)

which is the probability density for a sphere to have orientation

u at time t

given that it had orientation

at initial time t = 0. The rotational function

(t)isthencalculatedas

(t)=



2,1

(

u) Y

2,−1

(

)P (

u,t|

)=exp

−6D

(16.64)

where we have employed the orthogonality relations of the spherical har-

monics. As a consequence, the depolarized EACF of non-interacting sphere

dispersions is

(q, t) ∝ β

exp

−



+6D



. (16.65)

636 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

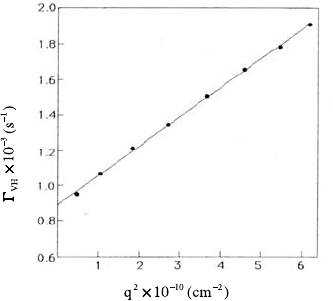
Fig. 16.3. Initial decay rate Γ

=−lim

t→0

(d/dt)lng

(q, t) of depolarized EACF

versus q

, for a dilute dispersion of anisotropic teﬂon spheres (Φ =0.02). After [12].

One can determine D

and D

simultaneously from the EACF by plotting the

time derivative of −ln g

(q, t)versusq

, yielding a straight line of slope D

and intercept D

. Plots of this kind are shown in Fig. 16.3 for depolarized

DLS experiments on a dilute dispersion of anisotropic teﬂon spheres [12].

The particle diameters determined from D

and D

, respectively, are indeed

nearly identical.

From employing the fundamental solution, one can further calculate the

orientation autocorrelation function



u(t) ·

u(0) =exp{−t/τ

} (16.66)

and the orientation MSD [13]

[

u(t) −

u(0)]

 =2



1 − e

−t/τ

→



t, τ

 t  τ

2 ,t τ

(16.67)

where τ

=1/(2D

) is the orientation relaxation time. The tip of

u(t)per-

forms, for t  τ

, a two-dimensional random walk on the tangential surface

touching the unit sphere at

. The MSD saturates to 2 for times t  τ

since |

u(t) −

u(0)|≤2 for all t. Typical values of τ

are 10

−4

−10

−3

swhich

implies the following sequence of time scale separations

 τ

≈ τ

 τ

(16.68)

valid for the translational/orientational self-diﬀusion of non-interacting glob-

ular particles.

16.3.2 Diﬀusion Mechanisms in Concentrated Colloidal Systems

While the diﬀusion of a non-interacting sphere is completely described by

its MSD, which is linear in time in the diﬀusive time regime t  τ

,various

16 Diﬀusion in Colloidal and Polymeric Systems 637

diﬀusion processes have to be distinguished in non-dilute dispersions of inter-

acting colloidal spheres. These diﬀusion processes are controlled by diﬀerent

diﬀusion coeﬃcients which become equal to each other only in the dilute limit

when the sphere interactions can be ignored. The spheres inﬂuence each other

indirectly through the solvent ﬂow ﬁeld in which they move. These so-called

hydrodynamic interactions (HI) propagate on a time scale τ

≈ τ

,sothat

they act quasi-instantaneously on the diﬀusive time scale where the fast mo-

mentum relaxations of the spheres are not resolved any more. HI aﬀects the

sphere dynamics but not the equilibrium microstructure, since as dissipative

forces they are not describable in terms of an interaction potential. In addi-

tion to the HI, the spheres can have potential interactions with each other

through excluded volume, van der Waals and screened electrostatic forces.

These direct forces become operative on the interaction time scale τ

,which

is the time after which a particle experiences a substantial change of the po-

tential interactions through a perceptible change in its next neighbor sphere

conﬁguration. Very roughly, τ

can be estimated for a ﬂuid-like suspension as

the time needed for a sphere to diﬀuse across its own radius, viz.

≈

, (16.69)

with typical values of 10

−4

−10

−3

s.Theshort-timeregimeτ

 t  τ

,for

DLS is thus well separated from the long-time regime t  τ

Self-Diﬀusion

For short times τ

 t  τ

, a sphere diﬀuses only over a distance small as

compared to its own size, and the dynamic “cage” of neighboring spheres has

thus hardly changed (as sketched in Fig. 16.4a). The sphere diﬀuses then, on

the average, in a potential minimum of the neighboring particles and is thus

inﬂuenced only by the instantaneously acting HI. A linear increase

W (t)=D

t, τ

 t  τ

(16.70)

of the MSD is thus observed at short times, with a short-time self-diﬀusion

coeﬃcient, D

, smaller than the Stokesian diﬀusion coeﬃcient, D

, at inﬁnite

Fig. 16.4. Schematic view of a particle cage around a colloidal sphere for (a) short

times τ

 t  τ

and (b) long times t  τ

638 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

dilution, owing to the slowing inﬂuence of HI. Note that the subscript s in D

stands for “self” and the superscript for “short”. At intermediate times t ≈

, the cage becomes distorted from its equilibrium spherical symmetry and

the sphere experiences an additional hindrance by potential forces. The cage

distortion implies a sub-linear time dependence of W (t). For long times t 

, a sphere has experienced many independent collisions with neighboring

spheres, as sketched in Fig. 16.4b.

This leads again to a linear time-dependence of W(t)

W (t)=D

t, t τ

, (16.71)

but with a long-time self-diﬀusion coeﬃcient, D

, smaller than the short-time

one. Summarizing,

0 ≤ D

≤ D

, (16.72)

and one can show that this ordering is valid independent of the type of

potential interactions. All three diﬀusion coeﬃcients are equal to D

in the

absence of interactions only, whereas D

is substantially smaller than D

for strongly interacting particles. On approach of a glass-transition point, a

particle gets eventually trapped in its next-neighbor cage, with a complete

blocking of its long-range motion characterized by D

≈ 0 (idealized glass

transition scenario). In contrast, D

> 0 since a sphere in a glass can still

perform short-time Brownian motion within its cage.

Using (16.37), D

can be expressed as a Green-Kubo relation



∞

dtφ

(t) (16.73)

i.e. in form of a time integral over the VAF. On the coarse-grained level

t  τ

,theVAF

(t)=2D

δ(t) − ∆φ

(t) (16.74)

of interacting spheres consists of a singular part proportional to D

,such

that (16.70) is retained from (16.37), and a long-lived negative part, −∆φ

(t),

originating from particle interactions (caging). One can show that ∆φ

(t) > 0

and (d/dt)∆φ

(t) < 0, consistent with D

. The regular part of the VAF

is thus negative and increases strictly monotonically towards its ﬁnal value

zero. As one expects intuitively, the collective retarding eﬀect of neighboring

spheres leads to anti-correlations in the particle velocity. The positive-valued

singular part in the VAF is the residual of the fast initial decay of velocity

correlations mediated through the intervening solvent, and manifests itself as

a δ-function for t  τ

(see Fig. 16.5).

Substitution of (16.74) in (16.37) gives

W (t)=D

t + τ



− D



−



∞

du(u − t)∆φ

(u) , (16.75)

where

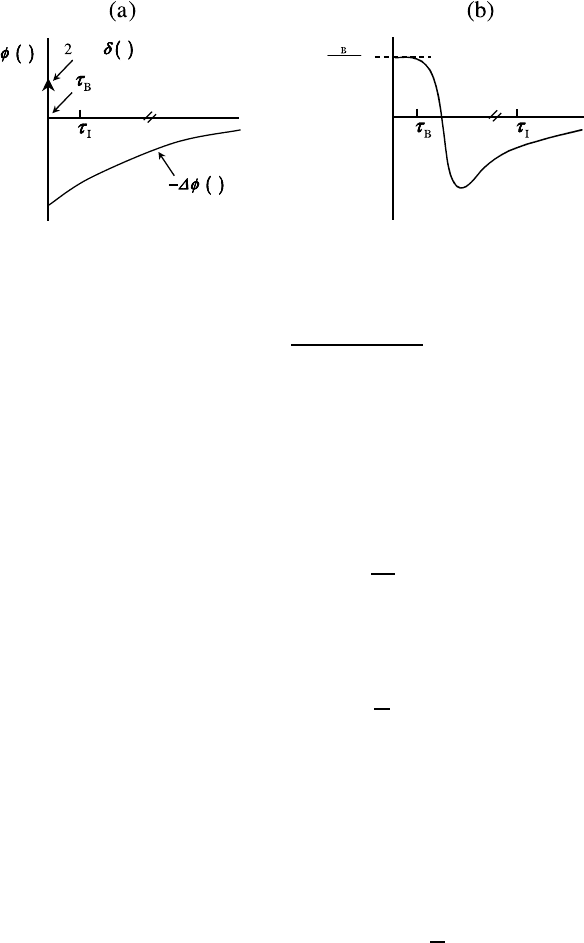
16 Diﬀusion in Colloidal and Polymeric Systems 639

Fig. 16.5. Schematic VAF in (a) the diﬀusive regime t  τ

, and (b) at very short

times so that the initial δ-peak is resolved.

≡

∞

dtt∆φ

(t)

∞

dt∆φ

(t)

(16.76)

is the mean relaxation time of ∆φ

(t). It is roughly comparable to τ

.The

last term on the right-hand side of (16.75) is the diﬀerence between W (t)and

its long-time asymptote. The asymptote crosses the vertical axis at the point



− D



. A remarkable feature of W (t) is that the approach towards

its long-time form in (16.71) is very slow. In three dimensions, the VAF of a

suspension of hard colloidal spheres has a negative long-time tail [14]

(t)=−∆φ

(t) ≈−A





−5/2

,t τ

(16.77)

with an amplitude A>0 that depends on the sphere concentration. The

MSD for large t is consequently

W (t) ≈ D

t + τ



− D





1 −





−1/2



+ O(t

−1

) , (16.78)

where τ

is a typical time scale related to τ

. Fig. 16.6 displays a sketch of a

three-dimensional MSD.

The relaxation of the VAF becomes extremely slow in two dimensions

where φ

(t) decays asymptotically as t

−2

for all concentrations, independent

of the nature of the interactions. Therefore, the two-dimensional MSD in-

cludes a logarithmic long-time correction [15]

W (t) ≈ D

t + τ



− D







+ O(1) (16.79)

with diﬀusion coeﬃcients and decay times diﬀerent from the three-dimensional

case. We emphasize that the negative VAF long-time tails discussed above

are due to conﬁgurational rearrangements of interacting spheres, and they

should not be confused with the positive long-time tail in (16.50). The latter