Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

660 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

1 − 0.63φ + O(Φ

). Thus, memory eﬀects in S

(t) lead to a mean diﬀusion

coeﬃcient only slightly smaller than the short-time one, to ﬁrst order in Φ.

Whereas a true long-time rotational self-diﬀusion coeﬃcient, D

does not

exist in monodisperse suspensions, we expect D

to be a well-deﬁned long-

time property when interpreted as the long-time coeﬃcient describing the ro-

tation of a large tracer sphere immersed in a dispersion of small host spheres.

Depolarized DLS measurements indicate that a tracer/host size ratio larger

than 10 is large enough for D

to be well-deﬁned. Due to the separation of

time scales between the slow motion of the tracer and the fast motion of the

host spheres, the tracer experiences the host dispersion as an unstructured ef-

fective ﬂuid, characterized by the eﬀective viscosity η

of the host dispersion.

Thus, one expects that D

obeys the generalized Stokes-Einstein relation for

a perfectly sticking eﬀective ﬂuid, i.e.

6πη

, (16.151)

where a

denotes the radius of the tracer. This expectation is supported

experimentally, and by calculating the short-time rotational self-diﬀusion co-

eﬃcient of the tracer in a dilute host dispersion of hard spheres [32]. For the

latter case, D

is described to good accuracy by [32]

= D



1 −

2.5

1+3λ

−1

Φ + O(Φ

)



, (16.152)

with λ = a

,andφ the volume fraction of host spheres. This equation

describes a monotonic decline of the tracer coeﬃcient from D

= D

at λ =0

towards D

= D

(1 − 2.5Φ)=k

T/[6πη

(1 + 2.5Φ)] + O(Φ

)forλ →∞

(see Fig. 16.12). For very large λ, the tracer sphere experiences thus the host

solution as an eﬀective one-component ﬂuid, with an eﬀective shear viscosity

given to ﬁrst order in Φ by the relation η

= η

(1 + 2.5Φ). In the opposite

limit λ  1 , the point-like (relative to the host) tracer rotates for short times

in an essentially stationary environment of host spheres so that its dynamic

cage is aﬀected only by the viscosity η

of the pure solvent.

16.4 Fluorescence Techniques for Long-Time

Self-Diﬀusion of Non-Spherical Particles

As explained above, in order to measure self-diﬀusion properties in a concen-

trated dispersion by means of light scattering, one needs to prepare a sys-

tem, where only a few particles scatter light (the so-called “tracer particles”),

whereas the majority of particles do not contribute to the scattered inten-

sity (the “host particles”). The tracer particles must be so dilute, that they

do not mutually interact, but may interact with the host particles. What is

then measured is the self-diﬀusion coeﬃcient at a concentration that is equal

16 Diﬀusion in Colloidal and Polymeric Systems 661

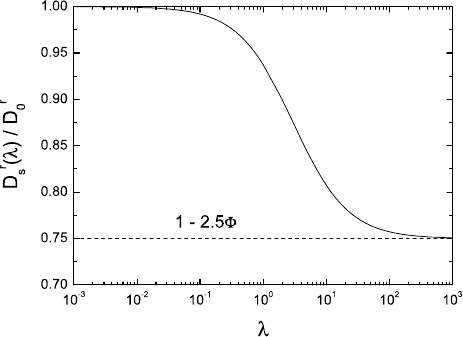
Fig. 16.12. Reduced short-time self-diﬀusion coeﬃcient D

versus size ratio

λ = a

of a colloidal tracer sphere immersed in a dilute host dispersion of

colloidal hard spheres. The volume fraction of host spheres is Φ =0.1. After [32].

to the overall concentration. Ideally, the pair-interaction potentials between

the tracer particles and host particles, and mutually between host particles,

are identical. Such a system is diﬃcult to prepare, especially for more com-

plicated colloidal particles such as rods or platelets. In addition, it is not

straightforward to obtain true long-time diﬀusion coeﬃcients by means of

light scattering. There exist other experimental techniques which allow for a

direct measurement of long-time self-diﬀusion coeﬃcients, without having to

resort to tracer systems. The techniques which will be discussed here are ﬂu-

orescent recovery after photobleaching (FRAP) and ﬂuorescence correlation

spectroscopy (FCS). Both these techniques require the colloidal particles to

be labelled with ﬂuorescent dyes.

16.4.1 Fluorescence Recovery After Photobleaching (FRAP)

Consider a monodisperse colloidal system, where each colloidal particle is

labelled with a number of ﬂuorescent dye molecules (such as Rhodamine or

Fluoresceine Iso Thio Cyanate (FITC)). These dye molecules can be exited by

a monochromatic incident light beam, and emit light of a larger wavelength

when the exited state of the molecule relaxes to a lower energy state. This

process is called ﬂuorescence. When the intensity of the incident beam is very

high, the structure of the dye molecules is irreversibly changed, and they loose

their ﬂuorescent properties. This process is called bleaching. A bleached dye

molecule does not ﬂuoresce anymore. In the early days of FRAP, diﬀusion

of free dye molecules was probed, by ﬁrst bleaching “a hole” in the sample,

by means of a short pulse of high intensity light. Then the intensity of the

662 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

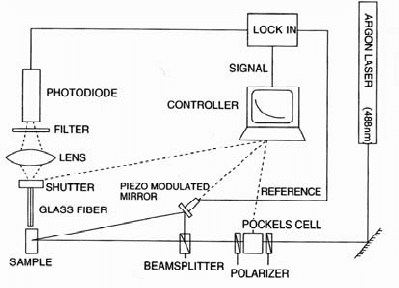
Fig. 16.13. Principle of a FRAP setup. Two beams are crossed under an angle

2 Θ. The mirror is mounted on a piezo element, which oscillates with frequency ω

during a measurement. A ﬁber picks up the ﬂuorescent light that originates from the

sample. The amplitude of the 2ω-component of the ﬂuorescent intensity is ﬁltered

out by means of a lock-in ampliﬁer. From [35].

incident beam was decreased to a level where bleaching is (virtually) absent,

and the ﬂuorescent intensity from molecules within the hole is detected as

a function of time. Due to diﬀusion of unbleached molecules from outside

the hole into the hole, and of bleached molecules from inside the hole out of

the hole, the ﬂuorescent intensity increases (“recovers”) with time. Once the

geometry of the bleached hole is known, the long-time self-diﬀusion coeﬃcient

can be obtained from the time dependence of the ﬂuorescent intensity. The

long-time self-diﬀusion coeﬃcient is measured here, since (i) the ﬂuorescent

intensity from diﬀerent molecules have no phase relation, so that interference

eﬀects on the measured intensity are absent (contrary scattered radiation),

and (ii) the size of the hole is much larger than molecular dimensions, so that

a signiﬁcant change in the ﬂuorescent intensity is only measured when the

molecules are displaced over distances that are large compared to their own

size.

The disadvantage of this older version of FRAP is that the geometry of

the bleached volume needs to be known, and that the ﬂuorescent intensity is a

very complicated function of time. Furthermore, for macromolecules that are

labelled, the time required for the ﬂuorescent intensity to recover would be

many hours. The FRAP technique was therefore improved (independently by

two groups [33,34]) by employing a diﬀraction grating or an interference pat-

tern, respectively. The technique described below uses an interference pattern

created by two crossing laser beams, as sketched in Fig. 16.13.

Instead of just bleaching a hole, a fringe pattern is bleached. To this end,

two laser beams are crossed under an angle 2 Θ,say,whichgivesrisetoa

standing interference pattern in the sample. For the intensity we have

16 Diﬀusion in Colloidal and Polymeric Systems 663

(r) ∼ cos{q

· r} , (16.153)

where the wavevector q

is equal to the diﬀerence between the wavevectors

and q

of the two crossed beams

= q

− q

. (16.154)

Its magnitude is equal to

4π

sin{Θ} , (16.155)

where λ is the wavelength of the laser beam. We note here, that for the

almost perpendicular incidence of the two beams onto the sample, the ratio

sin{Θ}/λ is independent of whether Θ and λ are both taken equal to their

values within the sample, or in air, in the absence of the sample. Typical

angles are Θ =1

◦

− 5

◦

, corresponding to a fringe spacings in the range

10 −50 µm. The bleach pulse now creates a sinusoidal concentration pattern

of bleached and unbleached particles, as sketched in Fig. 16.14, provided that

the amount of bleached dye molecules is proportional to the incident intensity.

The overall concentration (bleached + unbleached colloidal particles) is

constant. After this bleach of high intensity, the intensity is lowered to a value

where bleaching is virtually absent. Just as in the older version of FRAP, one

could now monitor the recovery of ﬂuorescent intensity with time. The mea-

sured ﬂuorescent intensity, however, is the sum of a background intensity

and a relatively small time dependent contribution. In order to increase the

signal-to-noise ratio of the FRAP experiment, instead, the interference pat-

tern is oscillated with a certain frequency ω and amplitude over the bleached

pattern. This is accomplished by sinusoidal motion of a mirror in Fig. 16.13

that is mounted on a piezo element, whereby the absolute phase of one of

the beams is changed by a phase angle Ψ. This so-called “reading intensity”

is then equal to

(r,t



) ∼ cos{q

· r + Ψ(t



)} , (16.156)

where

Ψ(t



)=A sin{ωt



} . (16.157)

The optimum value of the amplitude of oscillation A will be discussed later.

Since the ﬂuorescent intensity changes when the degree of overlap of the

reading fringes with the bleached fringes changes, the measured ﬂuorescent

intensity oscillates, generally in a complicated fashion. In addition, due to

diﬀusion the diﬀerence in concentration between bleached and unbleached

colloidal particles diminishes with time, resulting in a decreasing amplitude

of the oscillating ﬂuorescent intensity. The precise time dependence of the

ﬂuorescent intensity can be calculated as follows. First of all, the ﬂuorescent

intensity I

is proportional to the local incident intensity I

(r,t



)andthe

local concentration c

(r,t) of unbleached dye molecules (which are attached

to the colloidal particles), summed over the entire sample volume,

664 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier



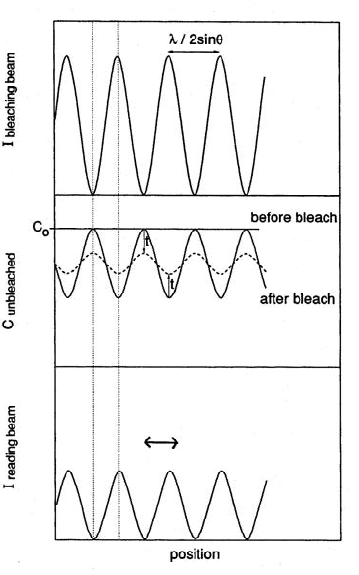
Fig. 16.14. The various stages during a FRAP experiment. The top ﬁgure is the

intensity of the sinusoidal fringe pattern within the sample. After the bleach pulse,

the concentration of unbleached particles is depicted in the middle ﬁgure. The

amplitude of the concentration proﬁle of unbleached particles diminishes with time

due to diﬀusion. The lower ﬁgure depicts the reading intensity with its oscillating

position within the sample. From [35].



,t) ∼



dr I

(r,t



) c

(r,t) ∼



dq I

(q,t



) c

(q,t) , (16.158)

where in the second equation, Bessel’s theorem is used to express the ﬂuo-

rescent intensity in terms of a wavevector integral over the spatial Fourier

transforms of I

and c

. We made here the distinction between the time de-

pendence t resulting from diﬀusion and the time dependence t



as a result

of the oscillating interference pattern. The reason for doing so is that the

frequency of oscillation will be assumed large enough, so that over a period

of many oscillations the concentration c

(r,t) hardly changes. This will be

important in order to be able to ﬁlter a certain time-Fourier component by

means of a lock-in ampliﬁer from the detected ﬂuorescent intensity. During

this ﬁltering, the time dependence due to diﬀusion must be negligibly small.

Since the spatial Fourier transform of I

in (16.156) is

16 Diﬀusion in Colloidal and Polymeric Systems 665

(q,t



) ∼ δ(q − q

)exp{iΨ(t



)} + δ(q + q

)exp{−iΨ (t



)} , (16.159)

where the δ’s are Dirac delta distributions, (16.158) leads to

(t, t



) ∼ c

,t)cos{Ψ (t



)} , (16.160)

where we used that c

,t)=c

(−q

,t). A time-Fourier analysis of the

ﬂuorescent intensity with respect to its t



-dependence is accomplished by the

mathematical identity

cos{A sin{ωt



}} = J

(A)+2

∞



n=1

(A)cos{2nω t



} , (16.161)

where J

is an m

order Bessel function. When the lock-in ampliﬁer is set

to ﬁlter the Fourier component with frequency 2ω, its output, according to

(16.160), (16.161), is equal to

S(t) ∼ c

,t) . (16.162)

S(t) is simply referred to as “the FRAP signal”. In an experiment, the am-

plitude A is chosen such that the corresponding prefactor J

(A) in (16.161)

is maximum. Now, since the fringe spacing is much broader than the lin-

ear dimensions of the colloidal particles, the ﬂuorescent intensity diminishes

only when colloidal particles are displaced over distances much larger than

their own size. Hence, long-time diﬀusion determines the time dependence

of the FRAP signal. Furthermore, since ﬂuorescent intensities from diﬀerent

dyes have no phase relation, the FRAP signal is not aﬀected by interference

eﬀects, so that self-diﬀusion in the homogeneous system governs the time de-

pendence. In the long-time limit, the concentration c

(r,t) obeys the diﬀusion

equation

∂c

(r,t)

∂t

= D

∇

(r,t) , (16.163)

where D

is the long-time self-diﬀusion coeﬃcient. The assumption here is

that bleaching has no eﬀect on the pair-interaction potential between the

colloidal particles. Hence,

∂c

(q,t)

∂t

= −D

(q,t) (16.164)

and

(q,t) ∼ exp{−D

t} . (16.165)

From (16.162) one thus obtains the following simple relationship between the

FRAP signal and the long-time self-diﬀusion coeﬃcient:

S(t) ∼ exp{−D

t} . (16.166)

666 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

The nice feature about the improved FRAP technique is that the concentra-

tion proﬁle of unbleached colloidal particles remains sinusoidal throughout

its relaxation, since the sine-function is an eigenfunction of the operator on

the right hand-side in (16.163). This feature leads to the single-exponential

behaviour of the FRAP signal in (16.166). This must be contrasted with the

concentration proﬁles during relaxation in the older version of FRAP, where

simply a hole is bleached, leading to a Gaussian-like concentration proﬁle af-

ter the bleach pulse. Such a Gaussian-like concentration dependence is not an

eigenfunction of the operator in (16.163), leading to a much more complicated

time dependence of the ﬂuorescent intensity during recovery as compared to

the decay of the FRAP signal in (16.166) for the improved FRAP technique.

The above analysis is a simpliﬁed version of a much more elaborate analy-

sis as given in [35].

Long-Time Self-Diﬀusion of Colloidal Rods

The analysis given above holds for colloidal particles of any shape, as long

as their linear dimensions are small compared to the fringe spacing. Experi-

mental results on spherical colloids (and mixtures of spheres of various sizes)

will be discussed later. In the present subsection we shall discuss FRAP ex-

periments on stiﬀ, colloidal rods, which are taken from [36–38].

Two colloidal systems are discussed here. The ﬁrst system consists of

boehmite rods, where the aluminium core is covered with aluminium chloro-

hydrate (Al

(OH)

Cl 2 −3H

O, ACH), to partly shield the van der Waals

attractions between the cores [38]. The aspect ratio, corrected for the ACH

layer thickness and charges of these rods is L/D =7.3(whereL = 257 nm is

the length of the rods, and D their eﬀective thickness). The solvent is water,

with 0.01 M added NaCl. This system will be referred to as “system I”. The

second system consist of boehmite rods, where the aluminium core is cov-

ered with a ∼ 25 nm thick layer of SiO

, which virtually completely screens

the van der Waals interactions [37]. The aspect ratio, corrected for charge

repulsion, is equal to L/D =5.4(withL = 323 nm). This system will be

referred to as “system II”. The solvent here is DMS with 0.01 M LiCl added.

The polydispersity in both systems is around 30 % in length and 20 % in

thickness. Both systems exhibit an isotropic-nematic (i-n) phase transition.

Typical FRAP data are shown in Fig. 16.15, together with a single-

exponential ﬁt (the solid lines) according to (16.166). The two sets of data

correspond to a measurement in an isotropic state and the coexisting nematic

state, where diﬀusion along the director is probed.

A reliable value for the long-time diﬀusion coeﬃcient, accurate to within

a few percent, is obtained when 10 to 20 such measurements are averaged.

Clearly there is a large diﬀerence between the long-time diﬀusion coeﬃcients

in the isotropic phase and the coexisting nematic phase. Within the nematic

state, where the orientation of the rods has a preferred direction, which is

referred to as the director, two kinds of diﬀusion coeﬃcients can be probed:

16 Diﬀusion in Colloidal and Polymeric Systems 667



Fig. 16.15. Typical FRAP curves (for system I). The two curves are for the nematic

state, where diﬀusion along the director is probed, and the coexisting isotropic state.

After [36, 38].

diﬀusion along the director and perpendicular to the director. In order to be

able to measure these two coeﬃcients, the wavevector q

in (16.154) must

be chosen either along or perpendicular to the director. The corresponding

FRAP geometries are sketched in Fig. 16.16, where the z-axis is along the

director.

Long-time diﬀusion coeﬃcients for system I are plotted in Fig. 16.17 as a

function of the bare volume fraction (where the thickness is not corrected for

the ACH layer thickness and charges). As can be seen, the long-time diﬀusion

coeﬃcients within the nematic phase are an order of magnitude smaller than

for the coexisting isotropic phase. Furthermore, the long-time self-diﬀusion

coeﬃcient D

nem,

for diﬀusion along the director is about twice as large as

the coeﬃcient D

nem,⊥

for diﬀusion in directions perpendicular to the director.

Side-wise diﬀusion is thus two times slower than length-wise diﬀusion in the

nematic phase. This kind of behaviour seems to be very sensitive on ﬂexibility

and/or the presence of charge interactions [39].

For low concentrations, in the isotropic state, the long-time diﬀusion co-

eﬃcient can be expanded with respect to the (eﬀective) volume fraction Φ

= D

1 − αΦ+ O



,

. (16.167)

On the basis of a variational approach for spherically end-capped cylinders

with hard-core interactions, the aspect-ratio dependence of the coeﬃcient α

is predicted to be equal (to within about 5 %) to [41]

α =2+

(p − 1) +

(p − 1)

,p≤ 30 , (16.168)

where p = L/D is the aspect ratio. Here, hydrodynamic interactions have

been neglected. For p = 1, that is for spherical particles, we have α =2.

668 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

(a)

(b)

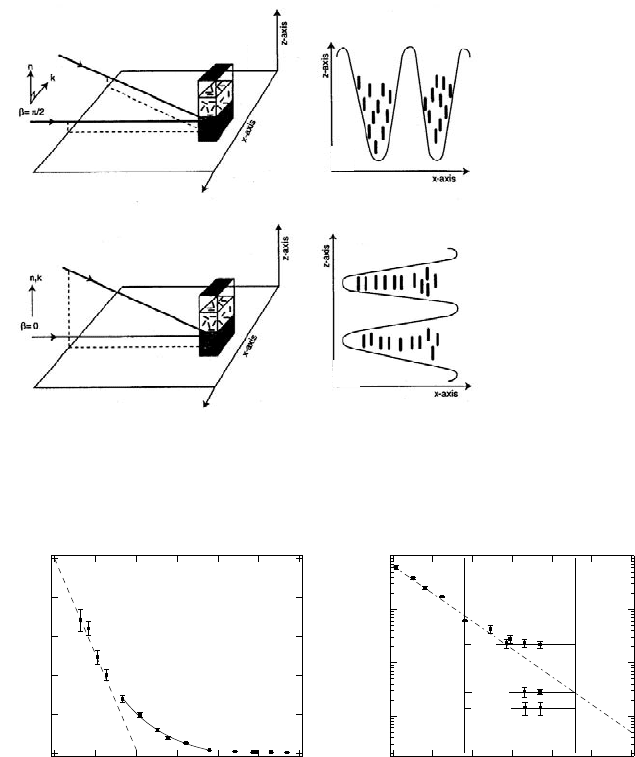
Fig. 16.16. FRAP geometries for the measurement of diﬀusion coeﬃcients per-

pendicular to the director (a) and parallel to the director (b). The ﬁgures on the

right depict the orientation of the fringe patterns relative to the director (which is

along the z-axis). After [36, 38].

1.0

0.8

0.6

0.4

0.2

0.0

30x10

-3

25201510

-2

-1

40x10

-3

3025201510

ISOTROPIC

NEMATIC

iso

nem, ||

nem,

⊥

Fig. 16.17. Long-time self-diﬀusion coeﬃcients for system I, as functions of the

bare volume fraction in the isotropic state (a), and up to volume fractions within

the i-n coexistence region (b). Diﬀusion coeﬃcients are normalized to the Stokes-

Einstein diﬀusion coeﬃcient D

. After [36, 38].

Including hydrodynamic interactions changes this value to 2.10 [1, 42, 43].

Since for rod-like particles the volume fractions of interest are lower than

those for spheres, this indicates that hydrodynamic interactions do not very

much aﬀect values for long-time self-diﬀusion coeﬃcients.

16 Diﬀusion in Colloidal and Polymeric Systems 669

Fig. 16.18. The coeﬃcient α, deﬁned in (16.168), as a function of the aspect ratio

p = L/D. The two curves are the result of a variational principle where a very

simple trial function is used (dotted line) and a more involved trial function (solid

line). The solid data points are computer simulation results from [40]. The open

circle is the FRAP result for system II. After [36, 37].

Experimental FRAP results for system I are not in accordance with this

theoretical prediction. Probably the 2 nm thick ACH layer does not eﬀectively

screen van der Waals attractions (a theoretical estimate for the minimum

layer thickness to fully screen van der Waals attractions of the aluminium

cores in water is about 20 − 30 nm). For the boehmite rods with the 25 nm

thick silica coating, system II, FRAP data are found to be in accordance

with the prediction in (16.168). The prediction (16.168), together with the

FRAP result for system II (open circle) and computer simulations (solid

data points) are plotted in Fig. 16.18. The two curves are the result of the

variational principle where a very simple trial function is used (dotted line)

and where a more involved trial function is used (solid line) [41]. It remains a

theoretical challenge to predict diﬀusion coeﬃcients at higher concentrations,

including the i-n coexistence region.

More FRAP data, for spherical particles, will be discussed later.

16.4.2 Fluorescence Correlation Spectroscopy (FCS)

In ﬂuorescence correlation spectroscopy one measures the ﬂuorescent inten-

sity that originates from a small, relatively strongly illuminated volume. Here,

a single laser beam is strongly focussed, and by means of confocal optics, the

ﬂuorescent intensity is measured from a region around the focal point, the

so-called “confocal volume”. The confocal optics is sketched in Fig. 16.19,

and explained in the caption.

The intensity distribution within the confocal volume is well represented

by a Gaussian proﬁle,