Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

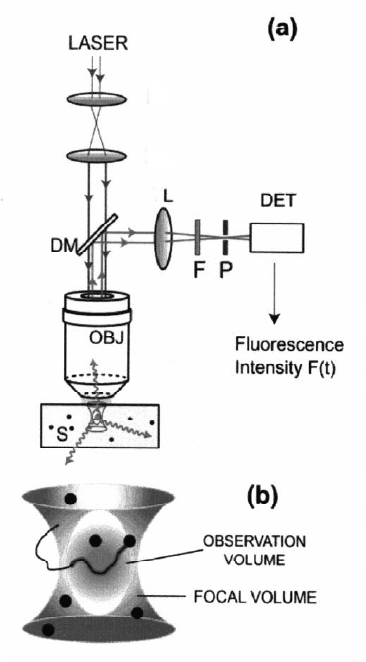
670 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

Fig. 16.19. (a) Typical conﬁguration of confocal optics as used in an FCS experi-

ment. A wide laser beam is strongly focussed by means of a high numerical aperture

objective (OBJ). The ﬂuorescent light is collected by the same objective, which is

reﬂected by a dichroic mirror (DM), and focussed by a lens (L) onto a pinhole

(P). The band ﬁlter admits ﬂuorescent light to the detector (DET). The region

from which ﬂuorescent light is detected is limited to a small volume (the so-called

confocal volume) by means of the pinhole P. (b) A magniﬁcation of the confocal

volume. Only that part of a macromolecule that is inside the volume contributes

to the measured ﬂuorescent intensity. After [44].

16 Diﬀusion in Colloidal and Polymeric Systems 671

(r) ∼ exp{−(x

+ y

)/2σ

} exp{−z

/2σ

} , (16.169)

where σ

measures the width of the confocal volume in the plane perpendic-

ular to the propagation of the beam, while σ

measures the length along the

propagation direction. Typically, σ

≈ 100−300 nm, and σ

≈ 200−600nm.

Similar to (16.158), the ﬂuorescent intensity is equal to

(t) ∼



dr I

(r) c

(r,t) , (16.170)

where c

is the local concentration of ﬂuorescent dye molecules, which are

(at least in part) attached to the colloidal particles. The time dependence is

now entirely due to the fact that colloidal particles diﬀuse in and out of the

confocal volume. What is neglected in (16.170) is the dependence of excitation

probabilities and ﬂuorescent intensities on the orientation of dye molecules.

This is probably a good approximation when there are many dye molecules,

with random orientations, attached to the colloidal particles. Contrary to

FRAP, the volume from which ﬂuorescent intensities are collected is assumed

to contain at most a single colloidal particle. At high concentrations this

sometimes requires to mix labelled with unlabelled colloidal particles. In a

FCS experiment, the intensity correlation function C

(t) ≡I

(t) I

(t =0)

is measured. From (16.170) we obtain

(t)=



(r) I



) c

(r,t) c



,t=0)

∼



(q) I



) c

(q,t) c



,t=0) , (16.171)

where in the second equation Bessel’s theorem has been applied twice, to

convert spatial integrations to wavevector integrations, which will simplify

the further mathematical analysis. Here, q-andq



-dependent functions are

understood to be spatial Fourier transforms with respect to r and r



, respec-

tively. Now suppose that there is at most a single ﬂuorescent colloidal particle

inside the confocal volume. The Fourier transform of the dye concentration

can be written as

(q,t)=B

(q,t)exp{iq · r

(t)} , (16.172)

where r

is the position coordinate (the position of the center of mass) of the

colloidal particle, and the “ﬂuorescence amplitude” B

is deﬁned as

(q,t)=



(t)

dr χ

(r)exp{iq · r} , (16.173)

where V

is the volume occupied by the colloidal particle with its center-of-

mass at the origin (as indicated by the subscript “0”), and

(r)isthechar-

acteristic function for the dye on and within the core of the colloidal particle

672 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

(χ

(r) = 1 when there is a dye molecule at r, and = 0 otherwise). The ex-

ponential with the position coordinate originates from the transformation to

the spatial integration with respect to a coordinate system where the center-

of-mass is chosen as the origin (similar as has been done in Sect. 16.2, dealing

with the principles of light scattering). The integral in (16.173) depends only

on the way dye molecules are distributed over its surface and possibly inside

its core. The volume V

is time dependent for colloidal particles where the

dye distribution is non-spherically symmetric, through the orientation of the

colloidal particle. Possible rotational contributions to the correlation function

C(t) originate from this integral. Such orientational contributions become im-

portant when the largest linear dimension of the ﬂuorescent macromolecule

are of the order of or larger than the dimensions of the confocal volume. In

that case, a mere rotation of the macromolecule can give rise to a change of

the ﬂuorescent intensity. Translational contributions originate from the time

dependence of the position coordinate r

. From (16.171), (16.172) we have

c

(q,t) c



,t=0)∼exp{iq · r

(t)} exp{iq



· r

(t =0)} . (16.174)

Since, for a homogeneous system, the probability density function P of

(t), r

(t =0)} depends only on the diﬀerence r

(t) − r

(t = 0), it fol-

lows that (with R = r

+ r



and ∆r = r

− r



)

c

(q,t) c



,t=0)

∼



P (r

− r



,t)exp{iq · r

} exp{iq



· r



}

∼





dR exp{i

(q + q



) · R}







d∆r P (∆r,t)exp{i

(q − q



) · ∆r}



. (16.175)

Since



dR exp{ i

(q + q



) · R}∼δ(q + q



) , (16.176)

where δ is the Dirac delta distribution, it follows from (16.175), that

c

(q,t) c



,t=0)∼c

(q,t) c

(−q,t=0)δ(q + q



) . (16.177)

This equation expresses translational invariance of a homogeneous system.

Substitution into (16.171) thus leads to

(t) ∼



dq I

(q) B

(q,t) B



(q,t=0)exp{iq · (r

(t) − r

(t =0))} ,

(16.178)

where “#” stands for complex conjugation. Note that, when the core of the

colloidal particle is homogeneously labelled, the ensemble average in (16.178)

16 Diﬀusion in Colloidal and Polymeric Systems 673

for the ﬂuorescence autocorrelation function is nothing but the electric ﬁeld

autocorrelation function in (16.20) that one would measure in a dynamic

light scattering experiment, provided that the scattering power is homoge-

neously distributed over the core of the particles. The ﬂuorescence correlation

function is a weighted q-average of the light scattering correlation function.

When the confocal volume is large compared to the linear dimensions of the

colloidal particles, the rotational contributions arising from the ﬂuorescence

amplitudes B

in (16.178) do not contribute to the time dependence of the

ﬂuorescence correlation function (in fact, numerical calculations for stiﬀ rods

show that this is already the case when σ

≥ L/2, with L the length of the

rods). Hence, for any practical application we have

(t) ∼



dq I

(q) exp{iq · (r

(t) − r

(t =0))} . (16.179)

Since the ﬂuorescent intensity only changes when the colloidal particle is

displaced over a distance larger or comparable to dimensions of the confocal

volume, which is in turn larger than the linear dimensions of the colloidal par-

ticles, the correlation function in the above equation is the long-time limiting

form as given in (16.165). Using that the Fourier transform of the Gaussian

proﬁle in (16.169) is given by

(q) ∼ exp{−(q

+ q

)σ

/2} exp{−q

/2} , (16.180)

where q

is the j-component of q, it is thus found that

(t) ∼



exp{−q

t + σ

}×



exp{−q

t + σ

}



exp{−q

t + σ

}∼





−1





−1/2

. (16.181)

The ﬂuorescent intensity autocorrelation function thus decays algebraically

with time, with the two time constants σ

1,2

. The geometrical constants

1,2

can be determined from a measurement of a dilute system where D

is equal to the Stokes-Einstein diﬀusion coeﬃcient, that can be obtained

independently from dynamic light scattering.

When the size of the particles is not small in comparison with the confocal

volume, the q-dependence of the ﬂuorescence amplitudes in (16.178) comes

into play. For spherical colloidal particles, in which the ﬂuorescent dye is

radially symmetrically distributed, the amplitudes are independent of time,

so that (16.178) simpliﬁes to

(t) ∼



eﬀ

(q)

exp{iq · (r

(0) − r

(t =0))} ,

where

674 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

eﬀ

(q)=I

(q) |B(q)|

is the Fourier transform of the intensity complying with an “eﬀective confocal

volume”. For homogeneously labelled spheres, | B(q) | can be represented

quite accurately by a Gaussian ∼ exp{−0.11 q

}, up to wavevectors where

B(q) is small enough that it does not contribute anymore to the integral over

q. Here, a is the radius of the spherical colloidal particle. We thus obtain the

“eﬀective size” of the confocal volume as

eﬀ

1,2

+0.22 a

When the particles are large, the ﬂuorescent intensity is non-zero already

when the outer part of a particle enters the confocal volume. At that moment

the center of the colloid is still outside the confocal volume. This leads to an

increase of the apparent confocal volume, as quantiﬁed for homogeneously

labelled spheres by the present expression for σ

eﬀ

1,2

Experimental correlation functions show some features that we have not

discussed above. First of all, in the various steps taken in the above analysis,

prefactors are always omitted. It turns out, by including all prefactors, that

the proportionality constant in (16.181) is equal to 1/[the average number

of ﬂuorescent colloidal particles in the confocal volume]. This reﬂects the

relative decrease of number ﬂuctuations in a given volume with increase of

volume. Secondly, there may be free dye molecules, not attached to colloidal

particles, in the solvent. When this is the case, there is a second, additive

contribution of the form (16.181), except that the time constants are much

smaller as compared to those for the colloidal particles. Free dye is therefore

seen only at very small times. Thirdly, dye molecules that are excited in

long-lived triplet states do not contribute to the ﬂuorescent intensity and

therefore temporarily reduce the number of ﬂuorescent dye molecules. Triplet

state excitation can thus be regarded as “reversible bleaching” (contrary to

the irreversible bleaching in the FRAP experiments described earlier). The

relative amplitude of such contributions depends on the sort of dye that is

used, as well as the concentration of dye on the surface and/or inside the core

of a colloidal particle.

A recent overview of FCS can be found in [44]. An extensive literature list

can be found on the FCS website of Zeiss. The above analysis is a simpliﬁed

version of a more elaborate analysis in [45].

As far as we are aware, there are no systematic FCS investigations pub-

lished on macromolecular systems. An example of a ﬂuorescence correlation

function on fd-virus (a semi-ﬂexible rod of length 880 nm and width of about

6 nm, with a persistence length of 2200 nm), labelled with TARAM , is given

in Fig. 16.20 [46]. At very small times a triplet contribution is found, at in-

termediate times a decay due to free dye and at longer times decay due to

diﬀusion of the fd-virus. The curve is ﬁtted with a sum of three terms: a

single exponential function to account for the triplet contribution, and a sum

of two contributions of the form as in (16.181) (one for the free dye and one

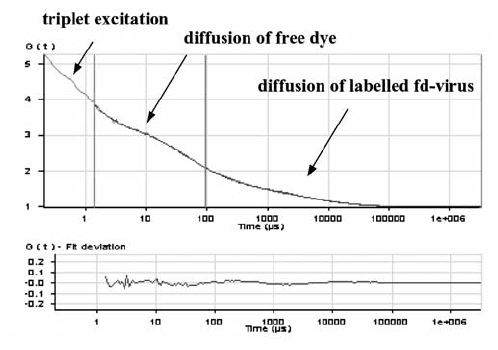
16 Diﬀusion in Colloidal and Polymeric Systems 675

Fig. 16.20. A ﬂuorescence correlation function for fd-virus, labelled with TARAM.

At small times a triplet contribution is clearly present, at intermediate times the

correlation function decays due to the presence of free dye molecules, and at larger

times due to diﬀusion of fd-virus. The lower part in the ﬁgure gives the residues

after a least-square ﬁt as described in the main text.

for the fd-virus). Clearly, the conditions should be optimized, in particular

to minimize the triple contribution.

16.5 Theoretical and Experimental Results on Diﬀusion

of Colloidal Spheres and Polymers

For times t  τ

, which is the regime of most DLS experiments, the veloci-

ties of the colloidal spheres have relaxed to equilibrium, so that only the slow

relaxation of the particle positions and orientations is probed. Therefore, the

dynamics of interacting spheres is entirely described on this coarse-grained

level in terms of a many-particle pdf, P (r

u,t), in the conﬁguration space

of positional and orientational degrees of freedom. The pdf depends thus,

in principle, on the center-of-mass position vectors r

=(r

, ··· , r

)and

orientation vectors

, ··· ,

)ofallN spheres in the suspension

(scattering volume) V

. The equation of motion for P (r

,t)isagener-

alization of the one-particle diﬀusion equation (16.45) to interacting parti-

cle systems. This many-particle diﬀusion equation is known among colloid

scientists as the generalized Smoluchowski equation (GSE). In the polymer

science community, it is better known as the Kirkwood-Riseman-Zimm equa-

tion [13, 47].

The description of the conﬁgurational evolution by means of the GSE is

founded on the separation of time scales between the fast ﬂuctuating parti-

676 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

cle velocities, and the slow conﬁgurational changes. Such a description can-

not be applied to polymer blends since the relaxation of the matrix, which

plays the role of the solvent, is comparable to those of the other compo-

nents. To explore the polymer dynamics in the diﬀusion limit (or Markovian

limit) of small wavenumbers and long times, we resort therefore to the semi-

phenomenological dynamic RPA. Using the RPA, we will study the interdif-

fusion process in a ternary homopolymer mixture.

16.5.1 Colloidal Spheres

Consider N identical colloidal spheres in a quiescent and unbound Newtonian

solvent. The evolution for the pdf of the particle positions alone

P (r

,t)=



P (r

,t) (16.182)

is described, for t  τ

, by the translational GSE

∂

∂t

P (r

,t)=

O(r

)P (r

,t) , (16.183)

where

O(r



i,j=1

∇

· D

) · [∇

− βF

] (16.184)

is the Smoluchowski diﬀerential operator. Here, F

= −∇

U(r

) denotes

the force that all other N − 1 spheres exert on sphere j, through potential

interactions U(r

). It is assumed here that the potential energy U (r

)isin-

dependent of orientation so that the particles exert no torques on each other.

Otherwise, the translational motion would be coupled to the rotational one.

The solvent appears in (16.183) only through the time-independent transla-

tional diﬀusivity tensors D

), which describe the solvent-mediated HI

between the spheres. The tensors D

) relate the hydrodynamic forces

}, exerted on the surfaces of the spheres by the surrounding ﬂuid to the

resulting drift velocity v

of a sphere i in form of a generalized Stokes’ law

= −



j=1

) · F

. (16.185)

The propagation of hydrodynamic disturbances (via sound and diﬀusion of

shear waves) appears to be inﬁnitely fast for times t  τ

. Therefore, the

HI between the spheres act quasi instantaneously on these time scales and

) can be determined, in principle, from solving the stationary lin-

earized Navier-Stokes equation describing the creeping ﬂow in an incompress-

ible ﬂuid, augmented by stick boundary conditions on the sphere surfaces.

Yet, actual analytical calculations of the D

) are very diﬃcult and have

16 Diﬀusion in Colloidal and Polymeric Systems 677

been fully achieved only on the pairwise-additive level, mainly in form of

inverse distance expansions. Hereby one disregards the inﬂuence of other

spheres on the HI between a given pair of spheres, an approximation which is

valid only for large interparticle distances. Note for spheres that the D

)

depend only on the positions. For non-spherical particles, HI couple position

and orientation variables. If we ignore HI, D

= δ

1 and (16.185) reduces

to the standard Stokes’ law for isolated single spheres.

In equilibrium, (∂/∂t)P = 0, and the GSE is satisﬁed by the equilibrium

pdf

)=exp{−βU(r

)}/



exp{−βU(r

)} (16.186)

independent of the D

). This shows that the HI are dynamic forces with

no eﬀect on static equilibrium properties.

Using the GSE, one can express equilibrium time-correlation functions

like S

(q, t)andS

(q, t)as

(q, t)=ρ

(−q)



exp{

t}ρ

(q)



, (16.187)

with A = a, c and microscopic densities ρ

(q)=ρ(q) (see (16.24)) and

(q)=exp{iq · r

}.Here



i,j=1



∇



· D

) ·∇

(16.188)

is the adjoint (or backward) Smoluchowski operator, and

··· =



)(···) (16.189)

is the equilibrium ensemble average. Note that

operates only on ρ

,and

not on P

In the following subsection, we describe theoretical methods based on the

GSE. From a theoretical point of view, it is appropriate to treat short-time

diﬀusion and long-time diﬀusion separately, since the former is needed as an

input to the latter one.

Short-Time Diﬀusion

In general, S

(q, t) cannot be calculated exactly from (16.187), owing to the

complicated form of the operator

for interacting particles. However, for

short times t  τ

, S

(q, t) can be expressed in a series of cumulants, that is

678 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

(q, t)=S

(q)exp



∞



l=1

(−t)

(l)

(q)



(16.190)

= S

(q)exp



−Γ

(1)

(q)t +

(2)

(q)t

+ ···



with S

(q)=S

(q, t). The higher-order cumulants, Γ

(l)

, with l =2, 3, ···,

measure the deviation of S

(q, t) from a single-exponential decay. Cumulant

analysis is a customary tool to analyze DLS data at short times, whereby

mainly the ﬁrst and second cumulants have been determined. One can al-

ternatively expand S

(q, t) in a time Taylor series, resulting in the so-called

moment expansion

(q, t)=

∞



n=0

(n)

(q)=S

(q)+tS

(1)

(q)+

(2)

(q)+... , (16.191)

with moments

(n)

(q)=

ρ

(−q)(

)

(q). (16.192)

In deriving (16.192), we have expanded the time evolution operator exp{

}

in (16.187) in powers of t. From a small-t expansion of (16.191), it follows for

the two leading cumulants that

(1)

(q)=−

(2)

(q)

(16.193)

(2)

(q)=

(2)

(q)

−



(1)

(q)



In specializing to A = c, the ﬁrst cumulant of the collective dynamic structure

factor follows as

(1)

(q)=q

H(q)

(q)

. (16.194)

Here, D

(q) is the apparent short-time collective diﬀusion coeﬃcient already

deﬁned in (16.98), and H(q)isgivenby

H(q)=



l,j=1



q · D

) ·

q exp{iq · [r

− r

]}. (16.195)

The function H(q) ≥ 0 contains, through the diﬀusion tensors D

, the in-

ﬂuence of HI on the short-time collective diﬀusion. For this reason, H(q)

is known as the hydrodynamic function. Without HI, H(q) ≡ 1, so that

(q)=D

(q)inthiscase.Anyq-dependence of H(q)isthusanindicator

16 Diﬀusion in Colloidal and Polymeric Systems 679

for the non-negligible inﬂuence of HI. Comparison with the phenomenological

(16.108) shows that

lim

q→0

H(q)=

. (16.196)

Hence, the long-wavelength limit of the hydrodynamic function is equal to

the relative (short-time) sedimentation velocity in a homogeneous suspension.

According to (16.195), H(q) is indeed a short-time equilibrium average.

Next, the ﬁrst cumulant for the self-dynamic structure factor is deter-

mined as (see (16.192))

(1)

(q)=q

, (16.197)

with the microscopic expression

= 

q · D

) ·

q (16.198)

for the translational short-time self-diﬀusion coeﬃcient. Without HI, D

since at short times the Brownian motion of a sphere is not inﬂuenced by

direct forces.

For large q  q

, strong oscillations in the exponential factors in (16.195)

cancel each other for l = j,andH(q) becomes therefore equal to the reduced

short-time self-diﬀusion coeﬃcient, i.e.

H(q  q

) ≈

. (16.199)

Likewise, D

(q  q

) ≈ D

since S

(q  q

) = 1. Thus, it is in principle

possible to determine short-time self-diﬀusion properties from DLS experi-

ments performed at long wavenumbers without a need for contrast variation.

Index matching is needed, however, to determine the MSD at longer times.

Moments up to the third order have been calculated for S

(q, t). The

expression for the second moment of S

(q, t)readswithoutHI

(2)

(q)=(q

)



βρ



dr g(r)(1− cos(q · r)) (

q ·∇)

u(r)



(16.200)

It is given in terms of the pair distribution function g(r), and derivatives of

the pair potential, u(r), between two spheres. Hereby it is assumed that the

total potential energy is pairwise additive, that is U(r



i<j

u(|r

−r

|).

The second cumulant, S

(2)

(q), of S

(q, t) is given by (16.200) with the cos(q·r)

term omitted, since

(q  q

,t)=S

(q, t) (16.201)

due to smallness of the distinct part, S

(q, t), of S

(q, t)forq  q

(cf.

(16.28)).

Little is known about the higher-order moments. With HI, even the sec-

ond moment becomes quite complicated, invoking now up to four-particle