Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

640 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

-1/2

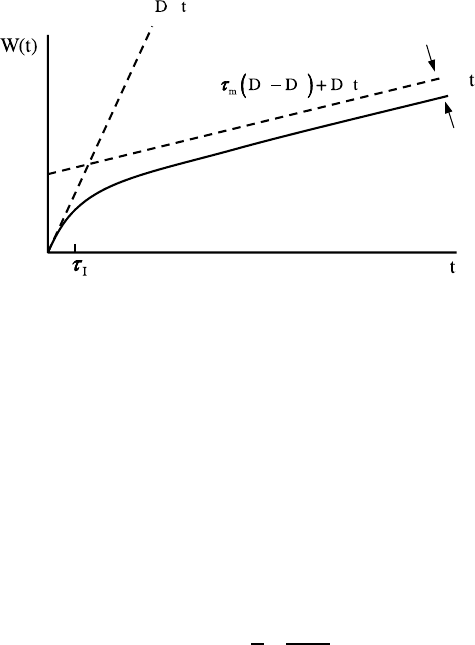
Fig. 16.6. Mean square displacement in three dimensions (for t  τ

is due to unsteady solvent ﬂow around a sphere in isolation, and appears on

a much shorter time scale t ≈ τ

The long-time decay of the VAF in one dimension is proportional to

−t

−(d+2)/2

,withd specialized to one. For particles diﬀusing along an inﬁ-

nite line which are not allowed to pass each other (single-ﬁling condition)

there is, however, a subtle diﬀerence to diﬀusion in higher dimensions. Due

to the strong mutual hindrance of particles moving along a line the MSD at

long times grows only proportional to t

1/2

. Without HI, the MSD reads thus

explicitly [16]

W (t) →

⎧

⎨

⎩

t, τ

 t  τ





1/2

,t τ

(16.80)

with n denoting the line density of particles and interaction time τ

1/(D

). It is most likely that only the pre-factor of t

1/2

will be aﬀected

when HI is included. The long-time limiting form of the pdf, P (x, t), for a

particle displacement x during time t is given by the Gaussian form in (16.40)

for d =1,withW (t) according to (16.80) for t  τ

. The absence of a linear

long-time term in W (t) implies a vanishing long-time self-diﬀusion coeﬃcient

for an inﬁnite line. Single-ﬁle diﬀusion can be observed, e.g., in superionic

conduction, in diﬀusion of bio-molecules through narrow-sized channels in

membranes and in zeolites of one-dimensional channel structure (cf., e.g.,

Chap. 10, Fig. 10.7, and Chap. 18, (18.107)).

Self-diﬀusion coeﬃcients can be measured by scattering experiments or

by means of specialized techniques that use ﬂuorescently labelled spheres

(which will be discussed separately later in this chapter). To measure self-

diﬀusion over an extended time range the system now consists of a possibly

concentrated suspension of host spheres, with a few tracer spheres, such that

the tracer spheres do not mutually interact with each other. The system

16 Diﬀusion in Colloidal and Polymeric Systems 641

must be prepared such that the scattered intensity from the host particles

and the solvent molecules can be neglected against that of the tracer parti-

cles. As explained in Sect. 16.2.2, the measured EACF is proportional to the

self-dynamic structure factor S

(q, t) deﬁned in (16.27), provided tracer and

host spheres are diﬀerent from each other only in terms of their scattering

properties.

The self-dynamic structure factor may be expanded in a Taylor series for

small wavevectors,

(q, t)=1−

|r(t =0)−r(t)|

+ O(q

) , (16.81)

meaning that

(q, t)=exp{−q

W (t)}

1+O(q

)

. (16.82)

There is a time-dependent non-Gaussian correction of O(q

)toS

(q, t)orig-

inating from particle interactions. This correction is rather small for a ﬂuid-

like suspension and becomes zero when the small-q limit is considered. Equa-

tion (16.82) allows for measuring the full time-dependence of the MSD. To

this end, −ln{S

(q, t)}/q

is plotted for a given time t against q

, and linearly

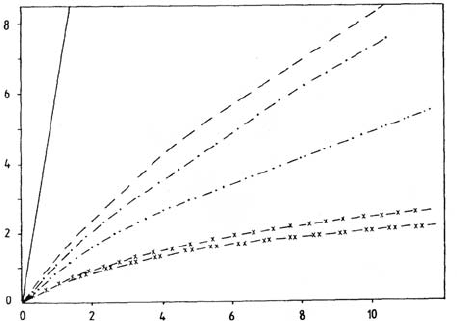
extrapolated to q = 0. The intercept is equal to W (t). Such data obtained

from dynamic light scattering experiments on hard-sphere suspensions are

given in Fig. 16.7, for various volume fractions [17]. The cross-over from

short- to long-time behavior is clearly seen. Further note the diminishing dif-

ference between the short- and long-time self-diﬀusion coeﬃcients when the

concentration is decreased.

At inﬁnite dilution, D

= D

, W (t)=D

t and

(q, t)=exp{−q

t}, (16.83)

which is the dynamic structure factor describing the single-particle diﬀusion

of independent particles.

Collective Diﬀusion

In contrast to self-diﬀusion, which is the Brownian motion of a tagged parti-

cle in a sea of others, collective diﬀusion refers to the isothermal relaxation

of density gradients by the coordinated motion of many colloidal particles.

Imagine a colloidal system where the density of colloidal particles, at some

instant in time, varies sinusoidally (such a sinusoidal density proﬁle is referred

to as a density wave or density mode). That is, at time t =0say,thenumber

density

ρ(r,t= 0) at position r is equal to

(r,t=0) = ρ

+ ρ(q,t=0)sin{q · r} (16.84)

with ρ

= N/V the average number density, and ρ(q,t = 0) the ampli-

tude of the density wave. The bar indicates an ensemble average over a

642 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

0.384

0.444

0.494

0.539

0.411

t 10 s

Wt( ) 10 ( m)

Fig. 16.7. Mean square displacement W (t) of silica tracer spheres in an index-

matched host suspension of PMMA spheres (of same size as the silica particles). The

curves are labelled by volume fraction Φ. The last two volume fractions represent the

co-existing ﬂuid (Φ

freez

=0.494) and crystalline (φ

melt

=0.539) phases. After [17].

non-equilibrium initial particle distribution. The wavevector q determines

both the direction and the wavelength of the sinusoidal density variation.

For changes of the position r in the suspension perpendicular to q, the phase

of the sine function does not change, so that the direction of q is in the “prop-

agation direction” of the sinusoidal variation. A change ∆r of the position r

parallel to q leaves the sine function unchanged when |∆r |= m ×2π/q,with

m an arbitrary integer. Hence, the wavelength of the density variation is

Λ =2π/q . (16.85)

The density wave will relax away to the homogeneous state due to the collec-

tive motion of particles. In the initial stage of relaxation (i.e. for τ

 t  τ

the decay of the density wave is single-exponential in time. At a later stage

(t ≈ τ

) the decay becomes non-exponentially and slower than initially as a

result of interactions between the colloidal particles. In the ﬁnal long-time

regime (t  τ

), the density variation may decay once again exponentially

in time for selected values of q, however with a decay rate that is usually

smaller than the initial one. For a density wave of large amplitude, diﬀerent

wavelengths come into play at a later stage and its shape is then no longer si-

nusoidal. Long-time collective diﬀusion describes the ﬁnal stage of relaxation

of a density wave, where the density proﬁle generally strongly deviates from

a sinusoidal proﬁle.

A phenomenological description of the relaxation of density waves can

be accomplished by using what is known as generalized hydrodynamics. The

starting point in a generalized hydrodynamic description is the continuity

16 Diﬀusion in Colloidal and Polymeric Systems 643

equation

∂

∂t

ρ(r,t)=−∇ ·j(r,t) , (16.86)

which relates the particle density to the particle ﬂux density,

j(r,t), and it

expresses the conservation of the number of particles. The overbar indicates

an average over a non-equilibrium ensemble. The ﬂux density

j(r,t)denotes

the number of colloidal particles that cross the point r in the direction in

which

j points, per unit area and unit time.

For small amplitudes in the density variation, and close to thermal equi-

librium, the ﬂux is linearly related to gradients in the density, that is (note

that at time t = 0 relaxation begins)

j(r,t)=−



(r − r



,t− t



) ·∇



ρ(r



) , (16.87)

where the integral kernel tensor D

(r,t) is referred to as the real-space col-

lective diﬀusion kernel. This phenomenological expression can be interpreted

as the leading term in an expansion of the ﬂux

j with respect to the ampli-

tude of density gradients. The “Taylor coeﬃcient” D

is independent of the

magnitude of gradients whenever these are suﬃciently small. Density modes

of diﬀerent wave numbers decay then independently from each other due to

linearity in

ρ(r,t). The non-local space and time dependence of j on ∇ρ can

be understood as follows. The ﬂux at a point r can depend on density gra-

dients at another point r



, through interactions between the spheres. Hence,

(r − r



,t− t



)=0when| r − r



| R

,whereR

is a measure for the

distance over which colloidal particles are correlated. Moreover, the ﬂux at

time t can depend on ∇

ρ at earlier times, due to the ﬁnite time it takes in-

teractions to propagate. Such time-delayed eﬀects are commonly referred to

as memory eﬀects. As a consequence, D

(r −r



,t−t



)=0whent −t



 τ

Note that causality requires that D

(r,t) = 0 whenever t<0. The diﬀusion

kernel is a tensor since ﬂux and density gradient may not be collinear. Spatial

isotropy requires further that D

(r,t)=D

(|r|,t). The so-called non-local

Fickian law in (16.87) is valid on a mesoscopically coarse-grained level of

spatial resolution ∼ (D

)

1/2

and time resolution ∼ τ

Spatial Fourier transformation of (16.86) with the use of (16.87) leads to

∂

∂t

ρ(q,t)=−q



(q, t − t



) ρ(q,t



) . (16.88)

where D

(q, t)=

q · D

(q, t) ·

q is the longitudinal part (parallel to q)of

the Fourier transform of the diﬀusion kernel, and

q = q/q. For notational

brevity we use the same symbols for the original and Fourier transformed

functions, where their argument (either r or q) indicates which function is

meant. Spatial isotropy requires the Fourier transform of D

(r,t) to depend

only on the magnitude q of the wavevector q. We learn from (16.88) that

644 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

the time rate of change of a density mode becomes increasingly slow with

decreasing wavenumber, since particles need to diﬀuse over an increasingly

large distance Λ =2π/q to smooth out density variations.

According to the deﬁnition of the collective dynamic structure factor, we

ﬁnd from (16.88) (using that the non-equilibrium average density

ρ satisﬁes

near equilibrium the same linear equation of motion as the equilibrium den-

sity autocorrelation function, which is known as an application of Onsager’s

hypothesis) that

∂

∂t

(q, t)=− q



(q, t − t



(q, t



) . (16.89)

The solution of this equation for S

can be formulated in terms of time-

Laplace transforms. The Laplace transform of a function f is deﬁned as

f(z) ≡



∞

dtf(t)exp{−zt} . (16.90)

In terms of such Laplace transforms, the solution of (16.89) reads

(q, z)=

(q)

z + q

(q, z)

(16.91)

with a wavenumber and frequency (i.e. z) dependent collective diﬀusion ker-

nel D

(q, z). As explained above, the q-dependence of D

(q, z) describes the

coupling between the colloidal particle ﬂux at a certain point with density

gradients at other points. The z-dependence of D

describes memory eﬀects,

that is, the coupling between the ﬂux at a certain time with density gradi-

ents that existed at earlier times. For strongly interacting particles memory

eﬀects give rise to a complicated time-dependence of S

(q, t), characterized by

a whole spectrum of relaxation times. The collective dynamic structure factor

(as well as S

(q, t)) is a strictly monotonically decaying function in time, for

ﬁxed q, with negative slope (d/dt)S

(q, t) < 0. This exempliﬁes an impor-

tant rule stating that any autocorrelation function is strictly monotonically

decaying in time when described within the overdamped colloid dynamics,

i. e., for t  τ

[18]. It follows readily that S

(q, z) > 0andzS

(q, z) <S(q).

These inequalities in turn imply with (16.91) that D

(q, z) and its associated

collective diﬀusion coeﬃcients are all non-negative, as one expects on phys-

ical grounds. For ﬁxed t, S

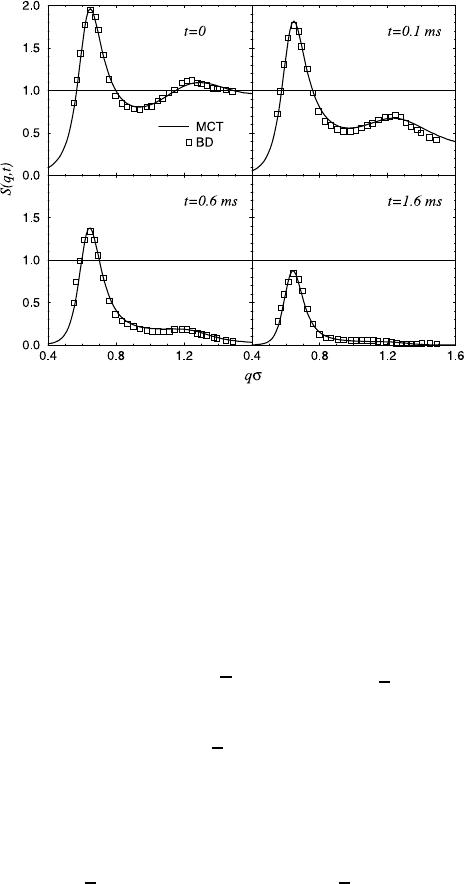
(q, t) shows damped oscillations in q.Atypical

q-dependence of S

(q, t)atvarioust is illustrated in Fig. 16.8, which shows

theoretical and computer simulation results of S

(q, t)forasuspensionof

charge-stabilized colloidal spheres.

There exists a special regime where (16.91) predicts an exponential decay

of S

(q, t). In this so-called hydrodynamic regime, only density wave relax-

ations are resolved with a wavelength much larger than R

(typically ∼ 1

mm), and with a time resolution that is much larger than τ

(typically ∼

16 Diﬀusion in Colloidal and Polymeric Systems 645

Fig. 16.8. Collective dynamic structure factor of a charge-stabilized colloidal dis-

persion. Open squares: Brownian dynamics (BD) computer simulations (from [19]);

solid line: Mode coupling theory (MCT) result.

1 s). On this strongly coarse-grained level, one can neglect non-local spatial

dependencies and memory eﬀects. The collective diﬀusion kernel is then equal

(r − r



,t− t



)=D

1 δ(r − r



) δ(t − t



) . (16.92)

The coeﬃcient D

is independent of position and time when the amplitude

of the density proﬁle is suﬃciently small. Hence, from (16.87),

j(r,t)=−D

∇ ρ(r,t) , (16.93)

which is Fick’s local law of macroscopic gradient diﬀusion. S

(q, t)andthe

associated density wave

(r,t) in (16.84) decay thus exponentially, for q 

−1

and t  τ

, according to

(q, t)=S

(q)exp{−q

t} (16.94)

and

(r,t)=ρ

+exp{−q

t} ρ(q,t=0)sin{q · r} (16.95)

respectively, where S

(q)=S

(q, t = 0) is the static structure factor. The

correlation length R

can be roughly estimated by 1/q

,whereq

is the wave

number where the static structure factor attains its principal maximum. The

average extension of the next-neighbor cage around a sphere is roughly equal

to 2π/q

. The local microstructure around a sphere is not resolved in the

hydrodynamic limit. This means that S

(q  q

) in (16.94) is practically

equal to the long-wavelength limit

646 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

(0) ≡ lim

q→0

(q)=ρ

Tχ

with χ



∂ρ

∂p



, (16.96)

where, for a one-component suspensions, χ

is the isothermal osmotic com-

pressibility of colloidal spheres.

The transport coeﬃcient D

is referred to as the long-time collective or

gradient diﬀusion coeﬃcient, since it can be determined, e.g., from macro-

scopic gradient diﬀusion experiments near equilibrium. Note here that (16.94)

is equivalent to

(q, z)=

(0)

z + q

. (16.97)

which shows with (16.91) that D

is equal to the small-wavenumber and

small-frequency (i.e. long-time) limit of the collective diﬀusion kernel. Ex-

plicitly

= lim

z→0

lim

q→0

(q, z) , (16.98)

where q

/z (i.e. q

t) is kept ﬁxed to a value of order one. The long-time

(i.e. zero-frequency) limit t →∞(i.e. z → 0) means in physical terms that

t  τ

(i.e. z  τ

−1

). Likewise, the short-time (inﬁnite-frequency) limit

t → 0(z →∞) should be interpreted as τ

 t  τ

(τ

−1

 z  τ

−1

As a phenomenological approach, generalized hydrodynamics provides no

methods to predict the collective diﬀusion kernel D

(q, z) and its associ-

ated long-time diﬀusion coeﬃcient D

. An actual calculation of D

(q, z)can

be accomplished only on the basis of a microscopic theory that relies on a

many-sphere extension of the single-particle diﬀusion equation (16.45) as the

appropriate time evolution equation. A microscopic theory of diﬀusion will be

discussed in Sect. 16.5. We will address here only general features of collective

diﬀusion.

At short times, τ

 t  τ

, memory eﬀects are not felt yet and

(q, t)=S

(q)exp{−q

(q)t}, (16.99)

i. e. there is an exponential short-time decay of S

(q, t) for all q. We recall

that short-time collective diﬀusion relates to the initial stage of relaxation of

a density wave, where it still retains its original form, but just has decreased

its amplitude. This process is described by a wavenumber-dependent (i.e.

apparent) diﬀusion coeﬃcient D

(q)=D

(q, z →∞) which quantiﬁes the

initial de-correlation of density modes of wavenumber q. Equation (16.99) and

the monotonicity of S

(q, t) imply that the longitudinal collective diﬀusion

kernel in (16.89) is decomposable as [18,20]

(q, t)=2D

(q)δ(t) − ∆D

(q, t) , (16.100)

corresponding to

∂

∂t

(q, t)=−q

(q)S

(q, t)+q



∆D

(q, t−t



(q, t



) , (16.101)

16 Diﬀusion in Colloidal and Polymeric Systems 647

with a memory function contribution ∆D

(q, t) ≥ 0. The non-local memory

eﬀect on density relaxations inherent in ∆D

(q, t) is operative only for times

exceeding the short-time regime, and it causes a slower and, in general, non-

exponential decay of S

(q, t).

The short-time collective diﬀusion coeﬃcient is deﬁned as the zero-q limit

of the apparent diﬀusion coeﬃcient

= lim

q→0

(q) , (16.102)

and relates to the long-time collective diﬀusion coeﬃcient through

= D

− lim

q→0



∞

dt∆D

(q, t) . (16.103)

The collective diﬀusion coeﬃcients obey thus the same ordering

≤ D

(16.104)

as the short-time and long-time self-diﬀusion coeﬃcients. The coeﬃcient D

quantiﬁes the relaxation of constant density gradients over times t  τ

through cooperative diﬀusion of spheres opposite to the gradient direction

q. Therefore D

is intimately related to the average sedimentation velocity,

, as measured in a homogeneous suspension of slowly sedimenting colloidal

spheres. To understand this explicitly, consider a homogeneous suspension

of equal spheres in a closed vessel which sediment slowly (so that Pe ≡

a/D

 0) under the inﬂuence of a constant force of buoyancy F = F

This force acting on each sphere drives a sedimentation ﬂux

= ρ

q . (16.105)

At equilibrium, the small concentration gradient, ∇

ρ, thereby generated will

produce an equal, but opposite diﬀusive ﬂux, j

,sothat

0=j

+ j

= ρ

q − D

∇ρ. (16.106)

The force on the solvent exerted by the sedimenting particles is balanced

through a pressure gradient, ∇p = ρ

F , generated by the base of the vessel

(which is perpendicular to

q). The pressure gradient drives a back-ﬂow of

solvent such that the zero-volume-ﬂux condition is fulﬁlled: due to incom-

pressibility, the net volume ﬂux of solvent and spheres through any plane

perpendicular to

q is zero. The concentration gradient (at constant temper-

ature and chemical potential) follows next from

∇

ρ =



∂ρ

∂p



T, µ

∇p = βS

(0)ρ

q . (16.107)

Finally, substitution into (16.106) leads to the general relation [21, 22]

648 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

(0)

(16.108)

between D

and U

,whereU

= βD

F is the sedimentation velocity at

inﬁnite dilution. Equation (16.108) can be derived more rigorously from linear

response theory, which provides us further with a microscopic expression for

Very interestingly, the conﬁgurational pdf of identical colloidal spheres is

not distorted from the equilibrium distribution during sedimentation, as long

as HI between spheres can be considered as pairwise additive. This holds true

for dilute monodisperse suspensions. The long-time sedimentation velocity

, which is measured in standard sedimentation experiments, becomes then

equal to the short-time sedimentation velocity U

. The latter is related to

the short-time collective diﬀusion coeﬃcient once again by (16.108), with l

replaced by s.Consequently

= D

(16.109)

for pairwise-additive HI. There is thus no distinction between short-time

and long-time collective diﬀusion, which corresponds to a vanishing memory

contribution to D

in (16.103). A density wave retains its sinusoidal shape

during the entire process of relaxation whenever the wavelength is much

larger than the correlation length R

. This result is in marked diﬀerence

to self-diﬀusion where the long-time self-diﬀusion coeﬃcient of interacting

particles is substantially smaller than the short-time one even when HI is

totally disregarded.

Three-body or more-body HI become highly relevant for concentrated

dispersions. In these systems, their eﬀect is to distort the suspension mi-

crostructure from the initial equilibrium distribution for times t ∼ τ

,which

causes additional hindrance of particle motion. For t  τ

,anewsteady-

state distribution has been reached, accompanied by a small decrease in the

sedimentation velocity such that U

and D

. Recent calculations

for dense hard-sphere suspensions have revealed, however, that the diﬀer-

ences between D

and D

are quite small (less than 6%), which makes them

diﬃcult to detect using DLS [23].

DLS and small-angle quasielastic neutron scattering experiments on col-

loidal particles which scatter equally strongly, are convenient and widely used

tools to determine S

(q, t) over an extended range of times and wave num-

bers. These methods allow one to study in detail relaxation of density waves

for a wavelength set by the experimental scattering angle. The short-time

and long-time collective diﬀusion coeﬃcients can be extracted from linearly

extrapolating −ln{S

(q, t)}/q

, measured for ﬁxed t  τ

and t  τ

, respec-

tively, to q = 0. The sedimentation velocity derives then from (16.108) when

in addition S

(q  q

) is determined by static light scattering.

In dispersions of strongly repelling particles, D

and D

can be substan-

tially larger than the Stokesian diﬀusion coeﬃcient D

. This feature is mainly

16 Diﬀusion in Colloidal and Polymeric Systems 649

Fig. 16.9. Enhanced relaxation of density ﬂuctuations through low osmotic com-

pressibility.

due to the low osmotic compressibility (i.e. S

(0)  0), which acts as a ther-

modynamic force driving the relaxation of local density gradients (cf. Fig.

16.9).

A typical concentration dependence of D

for a suspension of moderately

charged colloidal spheres and for a suspension of uncharged hard spheres is

shown in Fig. 16.10. Note that both S

(0) and U

decrease with increas-

ing volume fraction Φ of spheres (cf. (16.108)). At small volume fraction Φ,

decreases less strongly than S

(0) leading to an initial increase in D

With Φ further increasing, hydrodynamic hindrance starts to overcompen-

sate the electrostatic particle repulsion so that D

goes through a maximum.

The maximum in D

(φ) becomes smaller with increasing amount of added

electrolyte, i.e. with enlarged screening of the electrostatic repulsion. While

≤ 1 independent of the type of interactions, D

is found to be

larger than one for repulsive pair interactions. For dispersions with attractive

interaction contributions close to a critical point, however, D

≈ 0 due



Fig. 16.10. Theoretical prediction for the (reduced) collective diﬀusion coeﬃcient

versus volume fraction, for typical aqueous solutions of weakly charged

spherical micelles. Shown are two curves with (a) low amount and (b) moderately

large amount of added electrolyte. After [18].