Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

700 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

of interactions between the monomers and the incompressibility constraint,

but with the chain connectivity maintained. As a mean-ﬁeld-type theory, the

(dynamic) RPA should apply only to dense systems (i.e. melts) of suﬃciently

long polymer chains where density ﬂuctuations are small. Furthermore, its

predictions are most reliable for small values of q (as the ones probed in the

diﬀusive limit) since, as the name RPA implies, it involves an averaging over

the directions (phase) of q.

The mobilities {µ

αβ

}, with α, β ∈{A, B}, of an incompressible ternary

mixture are expressed in the dynamic RPA in terms of the mobilities, µ

αβ

of the bare system as [109]

αα

ββ

+ µ

(16.255)

αβ

= −



αα

ββ

αα

ββ



,α= β

where µ

is the mobility of a C-matrix monomer in the bare system. The

mobilities µ

αβ

are related to the self-diﬀusion coeﬃcients in the bare system

αβ

= δ

αβ

0α

, (16.256)

with D

0α

= k

T/γ

the self-diﬀusion coeﬃcient of an α-type monomer re-

lated to the monomer friction coeﬃcient γ

. This result for µ

αβ

is obtained

from adopting for the bare system the Rouse model for the dynamics of non-

interacting and non-self-avoiding Gaussian chains [13,106] (cf. also Sect. 13.4

of Chap. 13). Here, we use that in a dense system of chains like in a melt,

each chain is to a good approximation Gaussian and ideal, with R

∝ N

1/2

Within the Rouse model of non-interacting chains,

αβ

(q, t)=δ

αβ

exp{−q

0α

t} (16.257)

for qR

 1andfortimest large compared to the relaxation times of the

internal modes of a Rouse chain. Here, D

0α

is the center-of-mass self-diﬀusion

coeﬃcient of a polymer chain, related to the monomer diﬀusion coeﬃcient by

0α

= D

0α

,andp

is the degree of polymerization of an α-chain. Note

that S

αα

(q, t)/N

is the dynamic structure factor of a single Rouse chain. The

monomer friction coeﬃcient, γ

, enters the Rouse dynamics as a parameter

that must be speciﬁed as an input from elsewhere. Hence, γ

and D

0α

are

usually interpreted as the friction coeﬃcient and self-diﬀusion coeﬃcient of an

α-monomer in the actual mixture of interacting chains. As such they depend

implicitly on the composition and temperature of the mixture. Moreover, it is

then necessary to distinguish between systems of unentangled chains, where

= D

, and systems of very long chains governed by the reptation

process, where D

= D

[29,106].

16 Diﬀusion in Colloidal and Polymeric Systems 701

For an application of the RPA, consider ﬁrst an incompressible binary

blend, without any additional matrix molecules or vacancies. Substitution

of (16.255) and (16.256), with µ

set equal to zero, into (16.254) leads for

unentangled chains to

(Nx

)Λ





−1

, (16.258)

which is the slow-mode form for the long-time kinetic coeﬃcient (cf. (16.145)).

Recall here that the deﬁnitions of Λ

and S

in (16.130) and (16.117), respec-

tively, diﬀer from the ones used in this subsection by a factor of N (x

)

This factor renders them into intensive,i.e.N-independent, quantities. Ac-

cording to (16.258), the RPA predicts thus that the interdiﬀusion process in

a binary incompressible blend is dominated, for D

 D

,bytheslow

component A, which enslaves the dynamics of the fast component B in the

absence of voids.

To obtain D

, we need to divide Λ

by S

(q = 0). The latter is ob-

tained, for consistency, from the static limit of the RPA. For an incompress-

ible ternary blend of A and B chains in a matrix of C chains, the static RPA

relates the 2 ×2 static structure factor matrix, S(q, t), of A and B monomers

in the interacting system to the static structure factor matrix, S

(q, t), of the

bare system via (for details see [28, 106, 109])

S(q)

−1



(q)



−1

+ v(q) . (16.259)

Here, v(q)isa2×2 excluded volume matrix of elements v

αβ

(q), with α, β ∈

{A, B}, which accounts for the interactions between monomers of type α and

β, and for the incompressibility constraint.

The partial static structure factors of the bare system of non-interacting

Gaussian chains are explicitly

αβ

(q)=δ

αβ

([qR

Gα

]

) , (16.260)

where f

(x) is the Debye function [106], with f

(x) ≈ 1 −x/3forx  1, and

Gα

is the radius of gyration of an α-type chain. Using (16.260) specialized to

Gα

 1, the RPA result in (16.259) simpliﬁes for a binary incompressible

melt to

αα







− 2Nχ



. (16.261)

The Flory-Huggins interaction parameter, χ

, is related to the spatial

Fourier transforms, w

αβ

(q), of the local interaction potentials, w

αβ

(r), of

α and β monomers by [28, 106]

= lim

q→0



(q) −

(q)+w

(q))



, (16.262)

702 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

so that χ ≡ Nχ

can be interpreted as the Flory-Huggins interaction pa-

rameter per segmental volume v

= V/N,forequalsegmentalvolumesof

both polymer components. Typically, χ exhibits an inverse temperature de-

pendence. Finally, (16.258) and (16.261) yield



− 2χ





−1

. (16.263)

Experiments on binary blends (see the discussion given below) have re-

vealed that the slow-mode result does not satisfactorily describe, in general,

the dependence of Λ

on the molecular weight (say p

) of its constituents.

The observed discrepancy between the slow-mode result for binary incom-

pressible melts and experiment may be due to the presence of vacancies,

which add some amount of compressibility to the mixture. When instead of

a binary melt, a ternary incompressible blend of A and B chains in a matrix

of C-chains is considered, Λ

can be derived within the dynamic RPA from

substituting (16.255) and (16.256) into (16.251). This leads to the so-called

ANK expression,

(Nx

)Λ



+ x

−

− p

)

+ x



(16.264)

for the kinetic coeﬃcient of unentangled chains, originally derived by Akcasu,

N¨agele and Klein [28]. Quite remarkably, this expression reduces to the fast-

mode form (cf. (16.141)),

(Nx

)Λ

=[x

+ x

] , (16.265)

in the limit of a large self-diﬀusivity and/or large concentration of matrix

molecules, that is for x

 x

0α

. In this ’solution-like’ limit,

(q, t) decays in a superposition of two normal modes where, contrary to

the incompressible case, d

−

and, likewise, d

cannot be identiﬁed with the

interdiﬀusion process [28]. The slow-mode result is recaptured from the ANK

formula when the matrix is removed, i.e. for x

→ 0, resulting again

in an incompressible mixture of A and B chains. If one is allowed to stretch

the validity of the RPA result in (16.264) by allowing the matrix to consist

of vacancies instead of homopolymers, the ANK formula predicts a gradual

transition from the fast-mode form to the slow-mode form of Λ

,whenthe

vacancy concentration, or compressibility, of the mixture is reduced.

Having analyzed the implications of the dynamic RPA and the Flory-

Huggins model for the long-time interdiﬀusion in binary melts, we proceed

to scrutinize the RPA predictions against DLS and time-resolved static light

scattering experiments on binary homopolymer blends. In DLS experiments

on binary blends, an apparent diﬀusion coeﬃcient,

16 Diﬀusion in Colloidal and Polymeric Systems 703



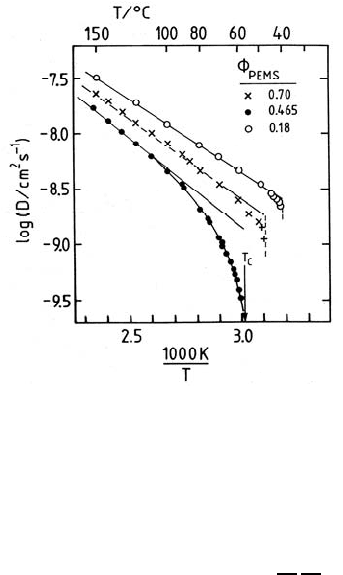
Fig. 16.29. Arrhenius plot of the apparent D for a binary blend of PDMS (p = 260)

and PEMS (p = 340) chains for three diﬀerent compositions of φ

PEMS

as indicated,

including the critical one at φ

PEMS

=0.465. The critical temperature T

=57

◦

is indicated by an arrow. The two non-critical data sets for D terminate at the

binodal phase-coexistence points. Data from [110].

D ≡−

∂

∂t

ln g

(q, t)|

t=0

, (16.266)

is determined, in the diﬀusive limit, from a cumulant analysis. Within the

RPA, D is identiﬁed with D

= Λ

in case of incompressility, with Λ

given by the slow-mode expression in (16.258). Fig. 16.29 shows DLS results

for D in the homogeneous one-phase region, for an almost symmetric mixture

of poly(ethylmethylsiloxane) (PEMS) chains of polymerization index p = 260

and poly(dimethylsiloxane) (PDMS) chains (with p = 340), with both indices

below the entanglement threshold. In this so-called Arrhenius plot, the loga-

rithm of D is plotted versus the inverse system temperature for three diﬀerent

volume fractions φ

PEMS

= x

PEMS

of PEMS, including the critical composi-

tion φ

PEMS

=0.465. This ﬁgure nicely illustrates, for φ

PEMS

=0.465, the

phenomenon of critical slowing down, when T is lowered in the one-phase

region to approach the temperature, T

, at the critical point of demixing (cf.

also Chap. 15, Fig. 15.14). Near the critical point, certain composition ﬂuc-

tuations become anomalously large, and diﬀusion becomes increasingly slow,

with D going to zero for T → T

. Demixing through spinodal decomposition

sets in when the temperature is lowered below T

. The critical point is the

location of a second-order phase transition, characterized by universal scaling

laws of its critical exponents (see [110] for details).

704 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

In the one-phase region T>T

,withT not too close to T

, the behavior

of S

and D

can be described by the mean-ﬁeld RPA, where the very small

values of D = D

near the critical point are ascribed to the divergence of

= S

(q = 0) at the spinodal line. The (mean-ﬁeld) spinodal line separates

the phase region of mechanical stability from the unstable one. The values of

the interaction parameter χ at the spinodal follow from (16.261) as

2χ

(φ)=

φp

(1 − φ)p

, (16.267)

with φ = x

and (1−φ)=x

. This allows us to reformulate the (slow-mode)

RPA result in (16.263) as

= φ(1 − φ) · 2[χ

(φ) − χ] · W

, (16.268)

with W

deﬁned by



(1 − φ)



−1

. (16.269)

We have factorized D

here in a geometric factor, φ(1−φ), a thermodynamic

factor, 2(χ

− χ), and in a kinetic factor, W

. The kinetic factor depends in

the unentangled case on the monomer diﬀusivities D

0α

= p

0α

and φ only.

For the following discussion, it is convenient to absorb a factor N [φ(1−φ)]

into the deﬁnitions of S

and Λ

, which renders them intensive. Using this

re-deﬁnition, S

is given by

2(χ

− χ)



φp

(1 − φ)p

− 2χ(T )



−1

, (16.270)

with zero values of S

at the end-points Φ =0, 1 of pure components, and a

parabolic shape of S

in between. For the kinetic factor then follows

φ(1 − φ)

= Λ

φ(1 − φ) . (16.271)

While (16.271) for W

has been derived for the incompressible case only, we

will employ it in an operational sense also for the interpretation of scattering

data, with the experimental D of (16.266) substituted in place of D

,andS

replaced by the experimental static structure factor S. The latter is obtained

using static light scattering from the excess Rayleigh ratio (cf. [111]).

When the slow-mode result in (16.269) applies, then 1/W

= φ(1 −

φ)/(DS) exhibits a linear φ-dependence. Measurements of D and of S for a bi-

nary mixture of poly(styrene) (PS) and poly(phenylmethylsiloxane) (PPMS)

chains [111] are indeed in favor of the RPA slow-mode result, as one can

realize from Fig. 16.30. The PS in the PPMS/PS acts as the slower and more

16 Diﬀusion in Colloidal and Polymeric Systems 705



0

0.5

1



Fig. 16.30. Variation of the inverse of the kinetic factor W

= DS/(φ(1 − φ))

versus volume fraction of PS, for blends of PS and PPMS (M = 2600), with PS

molecular weights M of 9000 (circles), 4000 (squares), and 2000 (triangles). Filled

symbols refer to T = 280 K and open symbols to T = 330 K. There is a linear

φ-dependence as predicted by the RPA slow-mode form. Data taken from [111].

’solid-like’ component, which reﬂects its stronger proximity to the glass tran-

sition point of pure PS. The blend demixes for larger values of φ

. Therefore,

values for W

are shown in Fig. 16.30 for the one-phase region only.

According to its deﬁnition in (16.271), and according to the fast-mode,

slow-mode and ANK results for the Λ

of unentangled chains, which depend

all on the segmental diﬀusion coeﬃcients D

0α

only, W

should be a local dy-

namic quantity, independent of the polymerization degree or, likewise, mole-

cular weight of the polymers. The predicted molecular-weight-independence

of W

= DS/(φ(1 − φ)) has been conﬁrmed [112] from static and dynamic

light scattering experiments on blends of poly(ethylmethylsiloxane) (PEMS)

and poly(dimethylsiloxane) (PDMS) polymers, where the molecular weight

of PEMS has been varied (cf. Fig. 16.31).



Fig. 16.31. Measured kinetic factor Λ = DS(q → 0)forablendofPDMS(p = 100)

and PEMS polymers at PEMS volume fraction φ

PEMS

=0.67 and T =20

◦

C versus

molecular weight, M

, of PEMS. The M

-independence of Λ for Rouse chains is

clearly seen. Data from [112].

706 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

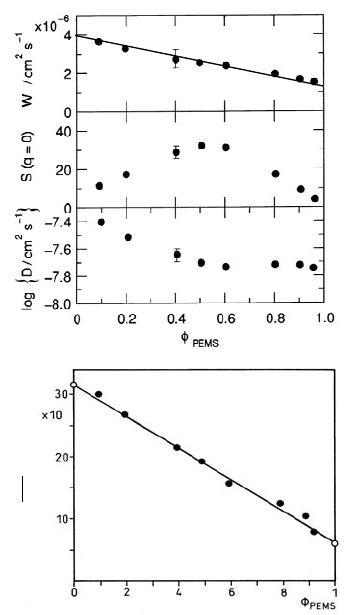
While the diﬀusion in certain binary blends, like PS/PPMS, is well de-

scribed by the RPA slow-mode result of incompressible systems, there is a

larger class of blends which conform to the fast-mode form of interdiﬀusion.

One well-characterized example is a nearly symmetric polysiloxane mixture of

low-molecular weight PDMS (p=80) and PEMS (p=90) polymers. Due to a

very distant glass-transition point, this system appears more as a ’liquid-like’

and compressible system. Experimentally determined values for D and S in

this blend as function of φ

PEMS

are listed in Fig. 16.32a, together with val-

ues for the kinetic factor determined from the operational equation (16.271).

The linear volume fraction dependence of W

is in accord with the fast-mode

result in (16.265). We note further that the measured S is well described by

(16.270).

There is an interesting relationship between the fast-mode behavior of

in PDMS/PEMS blends and their shear-mechanical properties. From

mechanical measurements of the low-shear-rate limiting viscosity, η

,inthe

blend, one can calculate a mean friction coeﬃcient, γ

, assuming Rouse

dynamics in a mixture [13],

36η

ρa

, (16.272)

where M

= φ

+ φ

and ρ = φ

+ φ

, respectively, are the

mean monomeric molecular weight and the mean mass density of the blend;

is the Avogadro number, and M the mean polymeric molecular weight

in the blend. Since mass transport by interdiﬀusion is related to the viscosity

in the medium, it appears likely that a generalized Stokes-Einstein relation

∝ k

T/γ

holds, provided that vitriﬁcation eﬀects due to the proximity

to a glass point do not play a role. A plot of 1/γ

versus φ should then

result in a linear composition dependence. Fig. (16.32b) proves that this is

the case indeed. From the fast-mode-like form of 1/γ

one concludes that

the inverse of the mean friction coeﬃcient can be expressed solely in terms

of the A and B monomer friction coeﬃcients, γ

in the blend, according to

−1

= φ

−1

+ φ

−1

The approximate fast-mode and slow-mode expressions for Λ

do ap-

ply only to selected polymer mixtures, with varying degree of accuracy

in each case. The fast-mode or vacancy model appears to be more con-

sistent with lower molecular weight blends, whereas the slow-mode or in-

compressible model is more consistent in the high molecular weight regime.

For an example of this trend, consider Figs. 16.33 and 16.34 which dis-

play time-resolved static light scattering data of Feng et. al [114] for the

kinetic interdiﬀusion factor (called mobility M in the notation of [114]) of a

poly(styrene)/poly(vinylmethylether) blend (PS/PVME) for varying molec-

ular weight N

of PS. In the experiments by Feng et al., the interdiﬀusion

coeﬃcient has been determined from temperature quench experiments within

the miscible one-phase region. The measured decay of density (composition)

ﬂuctuations right after the quench has been interpreted in these experiments

16 Diﬀusion in Colloidal and Polymeric Systems 707

(a)



o

(b)

s/kg

Fig. 16.32. (a) Apparent diﬀusion coeﬃcient D, measured static structure factor

S(q → 0), and kinetic factor W

for a nearly symmetric blend of PDMS (p=80)

and PEMS (p=90) versus composition φ

PEMS

at T =20

◦

C. The straight solid line

is the fast-mode prediction for W

. Data from [113].

(b) Inverse of the friction coeﬃcient, γ

, for the same PDMS/PEMS mixtures as in

(a), deduced from rheological measurements of the blend viscosity, η

, as explained

in the text. The linear composition dependence of 1/γ

veriﬁes a generalized

Stokes-Einstein relation W

∝ k

T/γ

for interdiﬀusion. Open circles at φ

PEMS

0, 1 refer to the pure components. Data from [112].

in terms of the celebrated Cahn-Hilliard-Cook (CHC) expression for the time-

resolved average scattered intensity of binary blends (cf. [29,114]). We remark

that the CHC expression is commonly used also to interpret the early stages

of spinodal composition of binary mixtures right after a sudden quench into

the mechanically unstable two-phase region.

The chains in the PS/PVME blend are in a bulk-entangled state, so that

the self-diﬀusion coeﬃcient of a chain scales, diﬀerent from Rouse chains, with

the inverse square of the molecular weight. In the entanglement case, W

not any more a local property independent of molecular weights. Substitution

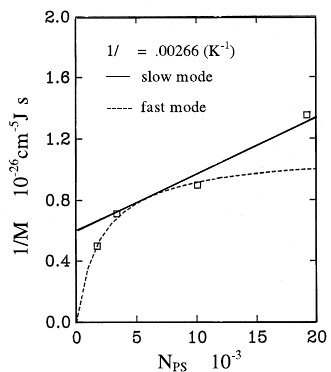
708 Gerhard N¨agele, Jan K. G. Dhont, and Gerhard Meier

Fig. 16.33. Inverse mobility data, M

−1

∝ 1/Λ

, versus molecular weight, N

,of

PS in PS/PVME blends. The dashed line (solid line) is a ﬁt of the fast-mode (slow-

mode) model to the experimental data. Both models show systematic deviations

from the data. After [114].

of D

0α

= D

0α

into (16.258), (16.265) and (16.264) leads for the inverse

mobility 1/M ∝ 1/(x

), according to the slow-mode expression, to

linear dependence on the degree of polymerization p

. On the other hand,

the fast-mode model predicts a concave curve for 1/M plotted versus p

with an inﬁnite slope at p

= 0 and a horizontal asymptote for large p

[29].

Fig. 16.33 includes experimental data of 1/M for four diﬀerent molecular

weights, N

, of PS. Neither the fast-mode nor the slow-mode expression

can adequately ﬁt the data. The fast-mode model applies only to the low-

molecular-weight side, and the slow-mode model only for large values of N

(cf. Fig. 16.33).

Inverse mobility data of PS/PVME versus N

for two diﬀerent tem-

peratures are depicted in Fig. 16.34, in comparison with the predictions of

the ANK formula. As one can see, the molecular weight dependence of the

kinetic factor in PS/PVME is well described by the ANK model, with the

(third) matrix component interpreted as ’vacancies’. The solid curves in Fig.

16.34 were plotted using the matrix parameter x

occurring in the

entanglement version of the ANK formula as a ﬁtting parameter. However,

this matrix parameter can be related to the cooperative diﬀusion coeﬃcient

in a binary mixture, which is a measurable quantity [29]. This deliberates us

from needing to assign a meaning to the diﬀusion coeﬃcient of a vacancy.

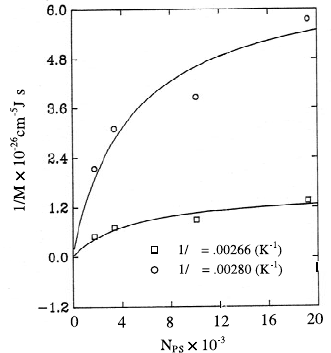
16 Diﬀusion in Colloidal and Polymeric Systems 709

Fig. 16.34. Inverse mobility data, M

−1

,versusN

, in PS/PVME blends at two

diﬀerent temperatures as indicated. The solid lines are ﬁts of the ANK formula

(16.264) to the data, demonstrating the applicability of the ANK-theory over the

whole range of PS molecular weights. After [114].

16.6 Conclusion

The aim of this chapter was to analyze the physics of various diﬀusion

processes observed in colloidal ﬂuids of spherical and rod-shaped particles,

and in binary polymer melts, to describe dynamic light scattering techniques

and other optical methods (FRAP and FCS) used for probing diﬀusion, and

to explain theoretical methods and computer simulation techniques which al-

low one to calculate diﬀusional transport properties and scattering functions.

Dynamic light scattering as described in Sect. 16.2 is nowadays a standard

technique to measure diﬀusion properties of colloids and polymers. The new

developments in this area are in the direction of scattering geometries, where

the dynamics under the inﬂuence of external ﬁelds (like pressure, shear ﬂow,

electric ﬁeld and temperature gradients), near walls and within interfaces

can be probed. In addition, somewhat slower dynamical processes are being

studied nowadays by means of optical microscopy, such as confocal laser

scanning microscopy (CSLM). Scattering from single colloidal particles can

be used to probe local properties in the possibly inhomogeneous system under

consideration.

Besides translational dynamics, FRAP can also be used to measure the ro-

tational dynamics, where the polarization dependence of excitation and emis-

sion probabilities are exploited. Time-resolved phosphorescence anisotropy

(TPA) has recently been used to measure rotational diﬀusion of colloids as

well [115, 116]. FRAP has been applied some time ago to probe long-time

diﬀusion under oscillatory shear ﬂow. A similar method is forced rayleigh