Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

13 Viscoelasticity and Microscopic Motion in Dense Polymer Systems 539

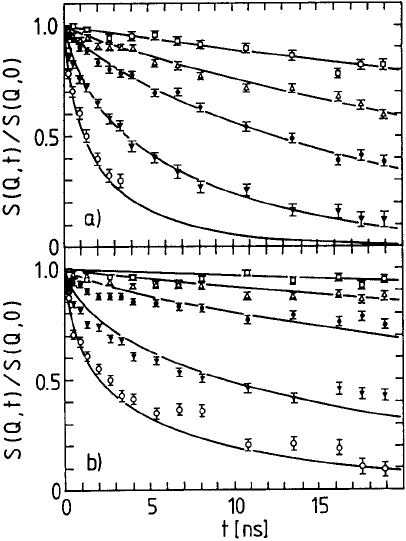
Fig. 13.19. Dynamic structure factors from PE-melts at 509K (a) M

= 2000; (b)

= 12400. The solid lines display the predictions of the Rouse model.

are compared with the dynamic structure factor of the reptation model [47]

and are very well described. We note, that the ﬁts were performed varying

only one single parameter, namely the tube diameter d, while the Rouse

rate was determined from earlier NSE data taken at short times. With this

one parameter it is possible to achieve quantitative agreement with respect

to both the Q and the time dependence of the dynamic structure factor.

We further note, that the dynamic structure factors predicted by the other

conﬁnement models discussed above are not able to ﬁt the data [16].

It is illustrative to visualize the large spread of the time regimes relevant

for the dynamics of the M

= 190000 molecule. The elementary Rouse time

amounts to 2.5 ps. The cross over time to local reptation τ

= 5 ns. The

Rouse time of the chain τ

=45µs and ﬁnally the disentanglement time

=11.7 ms. Thus, the relevant time scales spread over a range of more than

nine orders of magnitude. The corresponding length scales are much closer

together. The segment length  = 

√

∞

,whereC

∞

is the characteristic

ratio, is 4

A, the tube diameter d =46

A and the chain end-to-end distance

= 418

We are now drawing a third conclusion. NSE experiments on long-chain

polymer melts have veriﬁed the molecular existence of an entanglement length

540 Dieter Richter

Fig. 13.20. Scaling presentation of the dynamic structure factor from a M

36000 PE-melt at 509 K as a function of the Rouse scaling variable. The solid lines

are a ﬁt with the reptation model [47]. The Q-values (Q ≡ q) are (from above)

Q =0.05, 0.077, 0.115, 0.154

−1

Fig. 13.21. Dynamic structure factor from a long-chain PE-melt (M

= 190000)

at 509 K. The solid lines represent a ﬁt with the reptation model [47].

which, being of dynamic nature, under equilibrium only reveals itself in dy-

namic experiments. Moreover, the detailed Q-dependent dynamic structure

factor validates the idea of chain motion in a conﬁning tube and corroborates

quantitatively the celebrated reptation model of de Gennes.

13.6 Intermediate Scale Dynamics

A precondition for the validity of the entropy-driven Rouse model is the re-

quirement that only chain connectivity enters into the equation of motion and

any inﬂuence from local stiﬀness or rotational barriers etc. are negligible. In

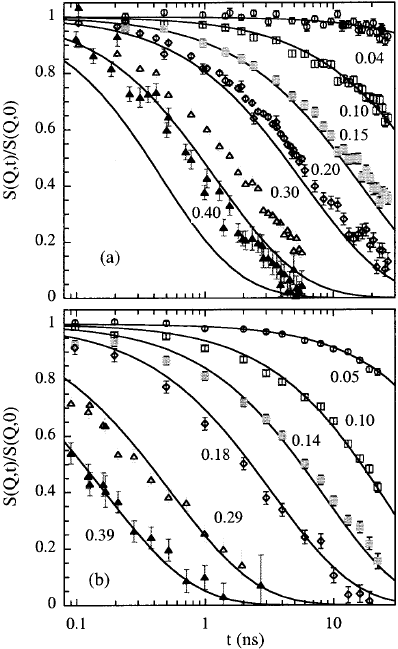
13 Viscoelasticity and Microscopic Motion in Dense Polymer Systems 541

Fig. 13.22. Dynamic structure factor of (a)aPIBmelt(M

= 3870, M

1.06, radius of gyration R

=19.2

A) at 470 K and (b) a PDMS melt (M

= 6460,

=1.10, R

=21.3

A) at 373 K. The Q-values (in

−1

)arenotedinthe

ﬁgures. The solid lines are the respective predictions of the Rouse model.

going to shorter length scales this condition must break down. Measurements

of the dynamic structure factor at smaller scales or higher Q-values oﬀer the

opportunity to learn about the limitation of the Rouse model towards local

scales and to understand the leading processes. Both local chain stiﬀness as

well as rotational potentials may play a role [49–51].

Recently, the relevant factors, which limit the universal Rouse dynamics

towards small scales, were studied in comparing the dynamic structure factors

S(Q, t) of polyisobutylene (PIB) and polydimethylsiloxane (PDMS) of simi-

lar size in the melt and in dilute solution [21,22]. Both polymers show similar

static ﬂexibility (the characteristic ratios are very close), but strongly diﬀer-

ent rotational barriers (PDMS: E

rot

∼

=0.4kJ/mol; PIB: E

rot

=12.6kJ/mol).

542 Dieter Richter

Figure 13.22a presents the dynamic structure factor from a PIB melt at

470 K including a ﬁt with the prediction of the Rouse model. Figure 13.22b

displays comparable data from a PDMS melt at 373 K.

While for Q-values above Q =0.15

−1

increasing deviations between

the experimental results from PIB and the Rouse prediction are evident, the

PDMS results are described well over the entire Q-range (up to Q =0.4

−1

Since both polymers exhibit the same static ﬂexibility, we may immediately

conclude, that chain stiﬀness is not the leading mechanism limiting the Rouse

dynamics for ﬂexible polymers as proposed earlier [51]. A thorough study of

the stiﬀness eﬀects on the dynamics of this polymer was carried out in [21]

applying the approaches of the all-rotational-state model and a bending force

model. Stiﬀness eﬀects were found to be almost negligible.

After the failure of stiﬀness models, the source for the slowing down of

the PIB chain dynamics at intermediate scales must be related to dissipation

eﬀects not present in PDMS. Allegra’s intrachain viscosity model [49,50] pro-

vides a simple access to such an eﬀect. He describes the intrachain dissipation

degrees of freedom by a local relaxation mode characterized by a relaxation

time τ

In order to access this process without disturbances experiments on so-

lutions were crucial, where interchain friction eﬀects are weak [22]. Fig-

ures 13.23a,b compare experimental results on PIB and PDMS in toluene

at room temperature and 378 K. While at low Q both data sets agree – both

polymers undergo the same translational diﬀusion – at larger Q a systematic

retardation of the dynamic response of PIB compared to PDMS is visible.

The application of the intrachain viscosity model to the PIB solution data

on the basis of the PDMS reference led to a very good description of the NSE

results for all Q values and temperatures (Fig. 13.24). The activation energy

of 13 kJ/mol for the intrachain relaxation time τ

agrees very well with the

rotational barrier for this hydrocarbon [52].

An application of the model to the melt data allows a quantitative de-

scription of the Q-dependent spectra. The activation energy for τ

resulted

to be about 40 kJ/mol, i.e. more than 3 times as high as in solution. Ob-

viously, chain relaxation occurs via correlated motions over several barriers

or interchain eﬀects come in additionally and the activation energy cannot

easily be compared with rotational potentials, see also [35].

Drawing a fourth conclusion, we note that Allegra’s intrachain viscosity

model accounts properly for the deviations from universal dynamics towards

shorter time and length scales. In solution, the corresponding relaxation time

directly relates to jumps across rotational potentials. Also in the melt, intra-

chain friction eﬀects limit the Rouse dynamics. The relaxation time, however,

is not directly related to crossings of single barriers.

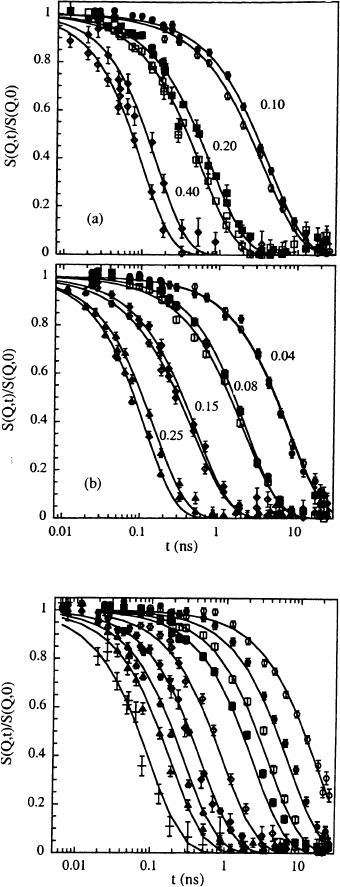
13 Viscoelasticity and Microscopic Motion in Dense Polymer Systems 543

Fig. 13.23. Chain-dynamic struc-

ture factor of PDMS (empty sym-

bols) and PIB (full symbols –

in each case the upper curve) in

toluene solution at 300 K (a) and

378 K (b). The corresponding Q (in

−1

) values are indicated. Lines

through the points are guides to

the eye.

Fig. 13.24. Chain-dynamic struc-

ture factor of PIB in toluene so-

lution at 327 K at the Q values:

0.04

−1

(◦); 0.06

−1

(•); 0.08

−1

(); 0.10

−1

(); 0.15

−1

(♦);

0.20

−1

(); 0.25

−1

(); 0.30

−1

(); 0.40

−1

(+). Solid lines cor-

respond to ﬁtting curves with the

Rouse-Zimm model including intra-

chain viscosity.

13.7 The Crossover from Rouse to Reptation Dynamics

Chains of small molecular weight are not able to build entanglements and

their dynamics is supposed to be fully compatible with the Rouse model.

Increasing the chain length beyond a threshold length, topological hindrance

shows itself in (i) reducing the self-diﬀusion coeﬃcient below the Rouse law

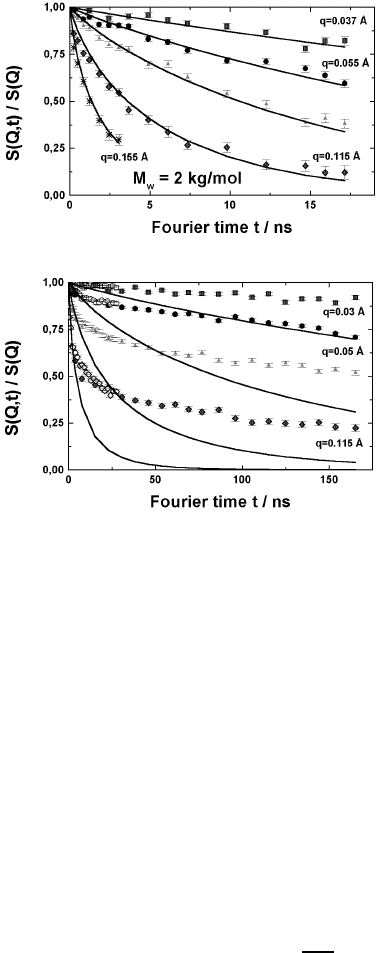
544 Dieter Richter

Fig. 13.25. Dynamic structure factor for two polyethylene melts of diﬀerent mole-

cular weight; a) M

=2×10

b) M

=4.8 × 10

. The momentum transfers Q are

Q =0.037; 0.055; 0.077; 0.115 and 0.155

−1

from top to bottom. The solid lines

show the result of mode analysis.

∼ 1/N and (ii) increasing the Rouse linear relationship between viscosity

and chain length to a power law η ∼ N

3.4

In order to ﬁnd out how beginning entanglement eﬀects inﬂuence the in-

trachain motions, we discuss neutron-spin echo experiments on a number of

polyethylene melts with molecular weights in the transition range (M

2000, 3600, 4800, 6500) [11, 13]. The monodisperse deuterated melts were

mixed with 10% protonated chains of the same length. Figure 13.25 shows

experimental spectra obtained on specimens with the molecular weights 2000

and 4800. A comparison of the spectra shows that the relaxation is obviously

much less advanced for the longer chain compared to the shorter chain. Let

us take the spectrum at the momentum transfer Q =0.12

−1

as an ex-

ample. While the dynamic structure factor for the shorter chain has already

decreased to about 0.1 after 20 nanoseconds, the longer chain only relaxes to

about 0.4 for the same Q and the same time.

In the following analysis of these data we want to ﬁnd out how the indi-

vidual normal modes of the relaxing chain are inﬂuenced by the appearance

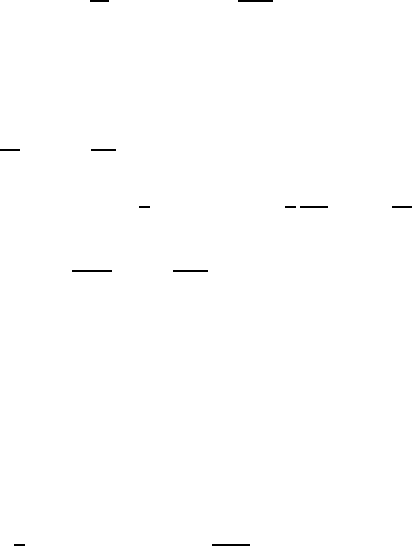
13 Viscoelasticity and Microscopic Motion in Dense Polymer Systems 545

of topological hindrance. The starting point for this analysis is the fact that

the spatial structure of the eigenmodes of Gaussian chains is given by the

Rouse form

(t)=



(t)cos



pπn



. (13.23)

The time dependence can have an arbitrary form. Within the framework of

this mode structure, the dynamic structure factor can be formulated in a

general form [53].

S(Q, t)=

exp



−



(t) − x

(0))









exp



−



|m − n|−





cos



pπm



cos



pπn



(1 −x

(t)x

(0))



(13.24)

where x

denotes the center of mass coordinates and the pointed brackets

denote the thermal average. The correlation function (x

(t) − x

(0))

 de-

scribes the diﬀusive motion of the molecular center of gravity. The relaxation

dynamics of the internal modes is hidden in the exact time dependence of

the correlators x

(t)x

(0). They describe the time-dependent development

of the motion of a normal mode “p”. In the case of the entropy-determined

Rouse motion, the correlators have the form

x

(t)x

(0)e

−t/τ



(t) − x

(0)]



Nζ

t = D

t (13.25)

where D

is the Rouse diﬀusion coeﬃcient. The beginning spatial restrictions

should lead to a more complicated time dependence.

How can we hope to extract the contributions of the diﬀerent normal

modes from the relaxation behaviour of the dynamic structure factor? The

capability of neutron scattering for directly observing molecular motions on

their natural time and length scale enables the determination of the mode

contributions to the relaxation of S(Q, t). Diﬀerent relaxation modes inﬂu-

ence the scattering function in diﬀerent Q ranges. Since the dynamic structure

factor is not simply decomposed into a sum or a product of mode contribu-

tions, this Q-dependence is not easy to represent. In order to make the eﬀects

more transparent, we consider the maximum possible contribution of a given

mode “p” to the relaxation of the dynamic structure factor. This maximum

contribution is reached when the correlator x

(t)x

(0) in (13.24) has fallen

to zero. In order to keep the picture simple, we retain all the other relaxation

modes: x

(t)x

(0) =1fors = p.

Under these conditions, (13.24) indicates the maximum extend to which a

particular mode p can reduce S(Q, t) as a function of the momentum transfer

546 Dieter Richter

Fig. 13.26. Contributions of the diﬀerent relaxation modes to the relaxation of

thedynamicstructurefactorS(Q, t)/S(Q, 0) for a) M

=2.0 × 10

and b) M

4.8×10

.TheexperimentalQ-values (in

−1

) are indicated by vertical lines; curves

correspond to mode numbers increasing from bottom to top.

Q. Figure 13.26 presents the Q-dependence of the mode contributions for the

= 2000 and M

= 4800 samples. Vertical lines mark the experimentally

examined momentum transfers. Let us begin with the short chain. For the

smallest Q the internal modes do not inﬂuence the dynamic structure factor.

There, only the translation diﬀusion is observed. With increasing Q,ﬁrstof

all, the ﬁrst mode begins to play a role. If Q is further increased, higher

relaxation modes above Q =0.1

−1

also begin to inﬂuence the dynamic

structure factor. If the chain length is enlarged, the inﬂuence of the diﬀerent

internal relaxation modes shifts to smaller momentum transfers.

This Q-dependent contribution of diﬀerent relaxation modes to S(Q, t)

permits a separation of their inﬂuence on the dynamic structure factor. In

order to be able to evaluate the data with a reasonable number of parameters,

as a ﬁrst approximation we assume that the exponential correlation of the

correlators (cf. (13.25)) is maintained. For further treatment reference is made

to [13].

13 Viscoelasticity and Microscopic Motion in Dense Polymer Systems 547

Fig. 13.27. Resultofthemodeanalysisfor

the M

= 3600 sample. The diagrams show

the result of a calculation of the spectra re-

taining a successively rising number of modes

in comparison to the experimental result; a)

translation diﬀusion only, b) translation dif-

fusion and ﬁrst mode, c) translation diﬀusion

and the ﬁrst two modes, d) translation diﬀu-

sion and the ﬁrst three modes, e) translation

diﬀusion and all modes.

The relaxation rates 1/τ

may depend in a general form on the mode

index p according to

1/τ

. (13.26)

The mode-dependent rate W

is the parameter of analysis.

Figure 13.27 demonstrates the contribution of diﬀerent modes to the dy-

namic structure factor for the specimen with the molecular weight 3600.

Based on the parameters obtained in a common ﬁt using (13.24) we cal-

culated S(Q, t) including an increasing number of mode contributions. Fig-

ures 13.27a show the contribution of translation diﬀusion. The translation

548 Dieter Richter

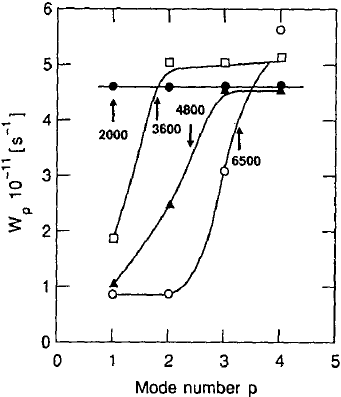
Fig. 13.28. Relaxation rates W

for the ﬁrst four relaxation modes

of chains of diﬀerent molecular

weight as a function of the mode

number p. The arrow indicates the

condition p = N/N

for each mole-

cular weight.

diﬀusion describes the experimental data for the smallest momentum trans-

fer Q =0.037

−1

. Figure 13.27b presents S(Q, t) retaining the ﬁrst mode.

Obviously, the long-time behaviour of the structure factor is now already

adequately represented, whereas at shorter times the chain apparently re-

laxes much faster than calculated. Figure 13.27c–e shows how the agreement

between experimental data and calculated structure factor improves if more

and more relaxation modes are included. In Fig. 13.27e, ﬁnally, very good

agreement between theory and experiment can be noted.

Figure 13.28 shows the results for W

, the mode-dependent relaxation

rate, for the diﬀerent molecular weights as a function of the mode index

“p”. For the smallest molecular weight M

= 2000 relaxation rates W

are

obtained which are independent of p. This chain obviously follows the Rouse

law. The modes relax at a rate proportional to p

(cf. (13.15)). If the molecular

weight is increased, the relaxation rates are successively reduced for the low-

index modes in comparison to the Rouse relaxation, whereas the higher modes

remain uninﬂuenced within experimental error.

How can we understand this behaviour? From the long-chain results of

the last section we know that for polyethylene at the measuring temperature

of 509 K the molecular weight between the points of entanglement is about

= 2000 or the number of monomers between the entanglement points is

= M

≈ 140 (M

: monomer weight). Let us assume that the charac-

teristic length for a relaxation mode L

is given by the distance between two

nodes (L

= N/p). We then may deﬁne a critical mode index p

= N/N

below which the characteristic extension of a mode becomes greater than the

distance between entanglements in the long-chain melt. These critical mode

indices for the diﬀerent molecular weights are plotted as arrows in Fig. 13.28.