Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

13 Viscoelasticity and Microscopic Motion in Dense Polymer Systems 519

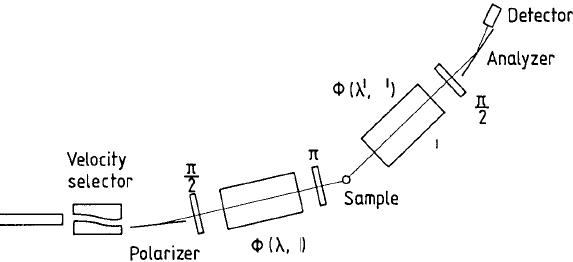
Fig. 13.3. Schematic representation of a neutron spin-echo spectrometer.

coil now only projects the x-component of polarization from a general direc-

tion into the z-direction. This part of the polarization is then identiﬁed by

the analyser. Apart from resolution corrections, the ﬁnal polarization P

obtained from the initial polarization P

= P



+∞

−∞

dωS(Q, ω)cosωt . (13.4)

The polarization P

is proportional to the Fourier transform of the scattering

function S(Q, ω). The transformation from δλ to ω gives the relation between

Fourier time, wavelength and magnetic ﬁeld as t ∝ λ

B.NSEisaFourier

technique, which measures the real part of the intermediate scattering func-

tion S(Q, t). The time variation in a spin-echo experiment is performed by

changing the magnetic ﬁeld.

Figure 13.4 shows a technical realization of the spin-echo spectrometer

at the J¨ulich FRJ-2 research reactor. Particularly striking are the Larmor

precession coils in front of and behind the specimen. Furthermore, some of

the coils for the spin angular operations can be recognized.

13.3 Local Chain Dynamics and the Glass Transition

The local chain motion under the inﬂuence of freezing processes is character-

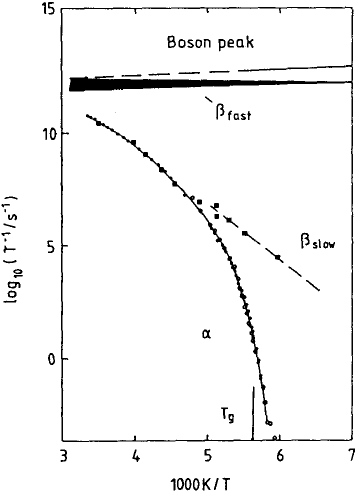
ized by a very broad range of time scales. Figure 13.5 displays a relaxation

map for (1–4) polybutadiene (PB) sketching the major dynamical features

of a glass-forming polymer. The shown data points are taken from dielec-

tric studies [27], from measurements of the dynamical modulus [28] and from

neutron scattering [4,7,29].

We distinguish three diﬀerent dynamical regimes:

(i) the freezing process is controlled by the structural α-relaxation exhibit-

ing a pronounced non-Arrhenius temperature dependence. Phenomeno-

520 Dieter Richter

Fig. 13.4. The neutron spin-echo spectrometer in the ELLA laboratory at the

FRJ-2 of FZ J¨ulich. The two large coils producing the precession ﬁelds are clearly

visible. The smaller Helmholtz coils are used for the spin angular operations.

logically it is well described by a Vogel-Fulcher temperature dependence:

−1

∝ exp(−B/(T − T

)).

(ii) At a temperature about 20% above T

a secondary relaxation process,

the β

slow

relaxation, splits from the α-process. Other than the primary

α-relaxation β

slow

follows an Arrhenius law and is not aﬀected by the

glass transition.

(iii) At high frequencies, in the picosecond range, characteristic low frequency

excitations – the Boson peak and the associated fast relaxation process

called β

fast

are indicated [30]. Following Fig. 13.5 the relevant time scales

for the glass process from the Boson peak and the fast relaxations to the

freezing α-relaxation span 14–15 orders of magnitude.

Though the relaxation dynamics of polymers has been investigated by

relaxational methods at least for ﬁve decades, still little is known about the

underlying molecular motions. In principle, varying the momentum transfer

Q, quasielastic and inelastic neutron scattering is capable of providing the

space-time resolution in order to access the relaxations on a molecular level. In

this section we discuss results from coherent quasielastic neutron scattering

on the relaxational dynamics in the α/β

slow

merging region [9, 14, 15] and

relate them to some recent incoherent (QENS) results on the self motion

[18,31].

13 Viscoelasticity and Microscopic Motion in Dense Polymer Systems 521

Fig. 13.5. Relaxation map

for (1–4) polybutadiene cover-

ing the prevailing dynamical fea-

tures around the glass transition.

The frequency range for the Bo-

son peak and the associated fast

relaxation-like dynamics (β

fast

)

are indicated schematically. The

full and open circle along the

α-relaxation trace represent di-

electric [27] and mechanical

[28] results, respectively. The

full squares display characteristic

rates obtained from neutron spin

echo spectroscopy [4,9]. The time

scale of the α-process has been

shifted to match that of the mi-

croscopic data. The dashed line

represents the temperature de-

pendence of the β

slow

process ob-

served by dielectric spectroscopy

[15].

13.3.1 Dynamic Structure Factor

We begin by displaying the qualitative behavior of the dynamic structure

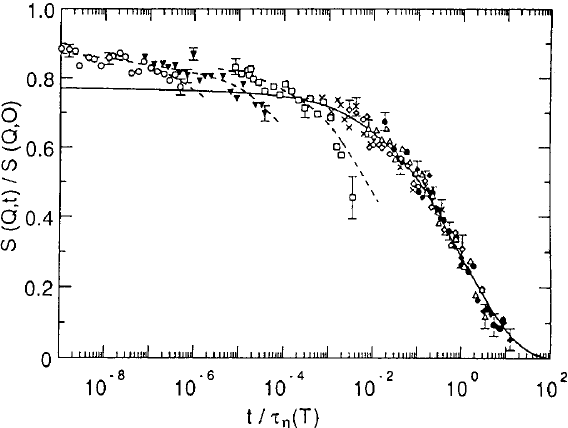
factor and then turn to a quantitative evaluation. Figure 13.6 shows the

intermediate dynamic structure factor as measured by NSE (cf. (13.1)) at a

Q-value close to the ﬁrst minimum of the static structure factor S(Q)[9].Ac-

cording to the time-temperature superposition principle the time dependence

of S(Q, t) was rescaled with the time scale of the α-relaxation as obtained

from dynamic mechanical measurements [32]. Above the merging tempera-

ture of the α and β

slow

relaxation T

≈ 220 K (see Fig. 13.5) the diﬀerent

spectra collapse to a single master curve following a Kohlrausch-William-

Watts (KWW) time dependence: τ

−1

KWW

∝ exp



−(t/τ

)



with β =0.41.

Below 220 K severe deviations from scaling are observed which are accompa-

nied by an increase of the amplitude of the relaxation function. As we shall

see this deviation from scaling is a signature of the β

slow

process.

We now inspect the Q-dependence of the dynamic structure factor in

more detail. Figure 13.7 displays NSE spectra taken at the position of the

ﬁrst and second peak of S(Q) – the ﬁrst peak or amorphous halo thereby

relates mainly to interchain correlations while the second peak stems from

intrachain distances. The data were rescaled with the time scale τ

set by

the viscosity relaxation. At the ﬁrst peak all data collapse on a single master

curve, which can be described by a stretched exponential using the dielectric

522 Dieter Richter

Fig. 13.6. Selected neutron spin echo spectra obtained at Q =1.88

−1

from

polybutadiene [14]. The time was rescaled to the viscosity scale. ( 280 K, • 260 K,

 250 K, ♦ 240 K, + 230 K,  205 K,  190 K, ◦ 180 K) The solid line represents the

master curve obtained from the spectra at temperatures higher than 220 K. The

dashed lines represent individual ﬁts to the low temperature data.

stretching exponent β

diel

=0.41. In contrast, at the second peak the spectra

do not follow the time-temperature superposition principle determined by τ

and strong deviations from a single master curve are obvious.

Extracting characteristic times from both sets of spectra, those from the

interchain peak follow, as already signiﬁed by the master plot, the Vogel-

Fulcher temperature dependence of the α relaxation, while those from the

second peak obey an Arrhenius law with an activation energy identical to

that of the dielectric β relaxation [14]. Thus, at the two ﬁrst structure factor

peaks qualitatively diﬀerent aspects of the chain dynamics are observed; at

the interchain peak the diﬀusive structural relaxation stands out, while at

the intrachain peak the more local β

slow

relaxation dominates the density

ﬂuctuations.

In the range of pure β

slow

relaxation below the merging temperature T

the main features of the dynamic structure factor can be understood in terms

of a simple model based on local jump processes with jump rates determined

by a Gaussian distribution of energy barriers as derived from dielectric re-

laxation. The β

slow

relaxation is assumed to be a spatially localized process.

The simplest picture of an elemental motion is a jump of an atom between

two equivalent sites separated by a distance d with a characteristic time

τ = τ

exp(E

T )whereE

is the activation energy and k

the Boltzmann

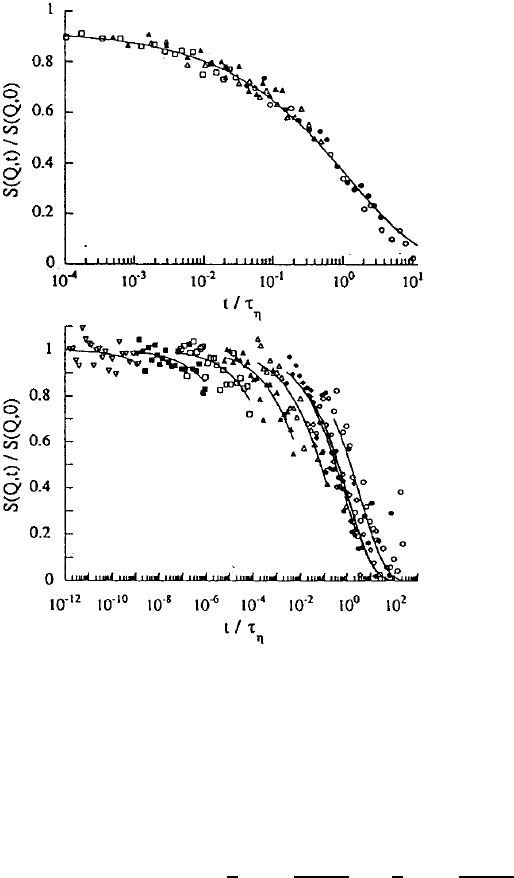
13 Viscoelasticity and Microscopic Motion in Dense Polymer Systems 523

Fig. 13.7. Scaling representation of neutron spin echo data from polybutadiene at

Q =1.48

−1

(◦ 280 K, • 260 K,  240 K,  230 K,  220 K (upper ﬁgure) and at

Q =2.71

−1

(◦ 300 K, • 280 K, ♦ 260 K,  240 K,  220 K,  205 K,  190K, |

180 K,  170 K). The solid lines correspond to KWW functions (see text) [15].

constant. For such hopping processes the incoherent intermediate scattering

function is given by

hop

inc

(Q, t)=1−



1 −

sin Qd





1 −

sin Qd



−2t/τ

=1− A

hop

(Q, d)+f

hop

(Q, d, τ, t) . (13.5)

Coherent and incoherent scattering diﬀer with respect to the presence of in-

terference terms in the coherent scattering. Let us consider the jump motion

of a pair of atoms. If such atomic jumps are uncorrelated, dynamic con-

structive interferences are absent and it follows naturally that the dynamic

quasielastic part assumes the form of the incoherent part. Note, however, that

524 Dieter Richter

interference terms from the average atom distribution remain giving rise to

S(Q). If the motions are correlated it can be shown that interference eﬀects

are small as long as the jump distances are smaller than the distances be-

tween atom pairs. Under this assumption the coherent inelastic part can be

approximated by the incoherent inelastic part, and the normalized coherent

scattering function can be written as

coh

(Q, t)

S(Q)

=1−

hop

(Q, d)

S(Q)

hop

(Q, d, τ, t)

S(Q)

. (13.6)

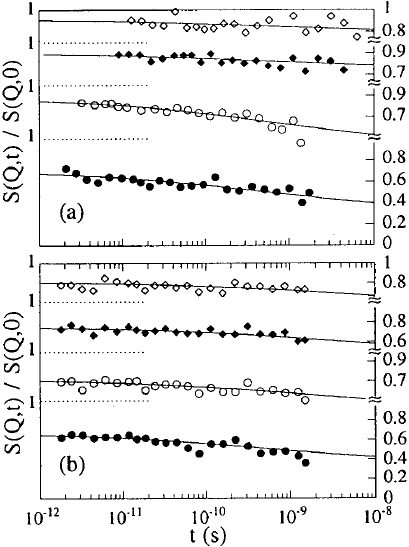
Figure 13.8 displays the result of the ﬁt with this model to the Q and T

dependent spectra. Implying for the jump distance the slight barrier energy

dependence of the soft potential model d ∝ E

1/4

a most probable jump dis-

tance of d =0.15 nm evolves. Furthermore, the experiment reveals the very

astonishing result that the density ﬂuctuations, which are directly observed

by the neutrons, decay two orders of magnitude faster than the dipole reori-

entations seen by dielectric spectroscopy (see also [33]).

The total scattering function for the β

slow

process then follows from an

averaging over the diﬀerent relaxation times with the energy barrier distrib-

ution from dielectric spectroscopy.

Figure 13.9 shows the relative quasielastic contribution of the β

slow

process

to the structure factor as calculated on the basis of the parameters obtained

by the ﬁtting procedure. The result explains immediately the qualitatively

diﬀerent behavior of S(Q, t)attheﬁrsttwomaximaofS(Q). Due to the

renormalization of the quasielastic part in (13.6) with S(Q) the contribution

of the β

slow

process at the ﬁrst maximum of S(Q) is minute, while it becomes

very strong close to the second maximum explaining the Arrhenius behavior

of the characteristic times at high Q. Further evaluation considering explicitly

the coherent form factor of the moving rigid building blocks of the chain (cis

and trans units involving the double bond) essentially conﬁrms the outcome

of the analysis within the simple hopping model [15].

At temperatures around the merging temperature T

and above, the time

scales of α-andβ-relaxations become similar and consequently the dynamic

structure factor has to be generalized in order to include the structural α-

relaxation or so-called segmental diﬀusion. When this segmental diﬀusion

reaches the timescale of the local relaxation, the atoms and molecular groups

will noticeably participate simultaneously in both motional mechanisms: the

intrachain β-relaxation and the interchain α-relaxation. We assume that to

ﬁrst order both mechanisms are statistically independent from each other.

We shall see that on the basis of this hypothesis the Q- and temperature-

dependent dynamic structure factors in the merging regime and above can

be consistently accounted for.

Being a conditional probability, the self-correlation function correspond-

ing to an atom undergoing two diﬀerent statistically independent motions,

α and β, can be written as a convolution product of the corresponding self-

13 Viscoelasticity and Microscopic Motion in Dense Polymer Systems 525

Fig. 13.8. Neutron spin echo spectra from polybutadiene a) at T = 205 K and

for diﬀerent Q-values ♦ 1.4

−1

,  1.56

−1

, ◦ 1.88

−1

, • 2.55

−1

; and b) at

Q =2.71

−1

for various temperatures ♦ 170 K,  180 K, ◦ 190 K, • 205 K. The

ordinates corresponding to each spectrum are given on the left and right side,

respectively. Solid lines correspond to the ﬁt with the hopping model for the β-

relaxation [14].

correlation functions:

αβ

(r,t)=



(r,t)G

(r − r



,t)dr . (13.7)

This implies that the incoherent structure factor obtained by Fourier transfor-

mation of G

αβ

(r,t) becomes a product of the structure factors corresponding

to the two processes:

αβ

(Q,t)=S

(Q,t)S

(Q,t) . (13.8)

In the coherent case the derivation of a similar expression is not straightfor-

ward because the correlations between all the pairs of scatterers (j, i)have

to be taken into account. It can be shown that a relation similar to (13.8)

holds if for the segmental diﬀusion the incoherent approximation is made.

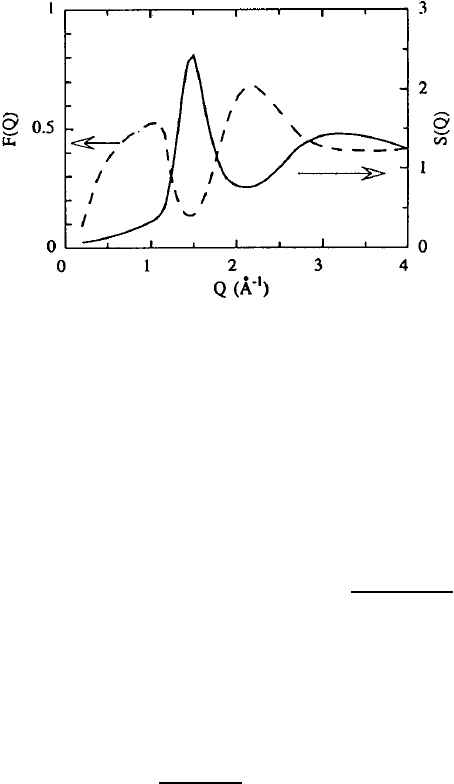
526 Dieter Richter

Fig. 13.9. Amplitude of the relative quasielastic contribution of the β

slow

process

to the coherent scattering function obtained from the hopping model as a function

of Q. The static structure factor S(Q) at 160 K is shown for comparison (solid

line) [14].

This assumption corresponds to the so-called Vineyard approximation [34],

in which S

coh

(Q, t) takes the role of S(Q).

In incoherent approximation the relaxation function for the α-process ϕ

can be described by a KWW function

(Q, t)=exp



−



KWW

(Q, t)





(13.9)

with β =0.41 from the shape of the dielectric spectra. τ

KWW

(Q, t)isthechar-

acteristic Q- and temperature-dependent relaxation time. With the structure

factor for the β-process evaluated at low temperature (see above) we obtain

similar to (13.8)

αβ

(Q, t)

S(Q)

= ϕ

(Q, t)S

coh

(Q, t)/S(Q) . (13.10)

All parameters involved in the coherent structure factor of the β-relaxation

are known from the evaluation at low T and are extrapolated to the higher

temperatures. Figure 13.10 shows the comparison between theory and exper-

iment for several temperatures at the ﬁrst maximum, minimum and sec-

ond maximum of S(Q) (Fig. 13.10a) and for 260 K at diﬀerent Q-values

(Fig. 13.10b). The excellent agreement between the scattering function

(cf. (13.10)) and the experiment strongly supports the hypothesis that the

α-andβ-relaxation occur independently of each other.

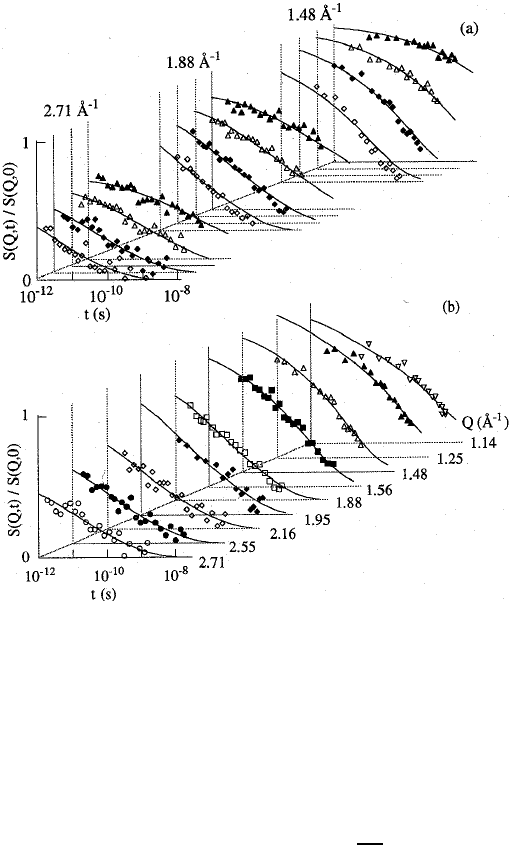
13 Viscoelasticity and Microscopic Motion in Dense Polymer Systems 527

Fig. 13.10. Data from polybutadiene: (a) NSE-spectra for the Q-values indicated

at 220 K (); 240 K (); 260 K () and 280 K (♦). (b) at 260 K for the Q-values

indicated. The solid lines display the model predictions.

13.3.2 Self-Correlation Function

In Gaussian approximation [20] the self-correlation function for a diﬀusive

process is directly related to the mean square displacement r

(t) by

self

(Q, t)=exp



−

r

(t)



. (13.11)

It is measured by analyzing the incoherent scattering from protonated sam-

ples. For the α-process the scattering functions are well described by stretched

exponentials (see (13.9)). It is worthwhile to note that (13.11) is completely

equivalent to the expression for spin-echo attenuation ((10.18) of Chap. 10

with the product D∆ expressed by the mean square displacement) of pulsed

ﬁeld gradient NMR, whence in the latter technique the quantity γδg assum-

ing the position of Q is sometimes referred to as a generalized scattering

vector.

528 Dieter Richter

If the system is homogenous, i.e. all particles undergo the same fate on the

time scale of observation, then a combination of (13.11) and (13.9) implies

r

(t) =

and τ

KWW

(Q) ∼ Q

−2/β

(13.12)

invoking sublinear diﬀusion of the polymer segments as the underlying rea-

son for the stretched exponential dependence. Its signature is a power-law

dependence of the Kohlrausch-Williams-Watts relaxation times τ

KWW

with

an exponent 2/β.

Figure 13.11 displays the τ

KWW

values obtained by backscattering spec-

troscopy (see Chap. 3) for four diﬀerent polymers, polyvinylether (PVE) at

340 K, polyisobutylene (PIB) at 365 K, polybutadiene (PB) at 280 K and

polyisoprene (PI) at 340 K for diﬀerent momentum transfers [20]. To test

(13.12), the relaxation times have been exponentiated with the exponent β

obtained from the stretching of the relaxation functions in these polymers by

dielectric spectroscopy. According to (13.12) τ

KWW

should be proportional

to Q

−2

. The solid lines in Fig. 13.11 display this power law relation. As may

be seen, in all cases the predicted power law within experimental error is

followed by the experimental relaxation times. Recent data on PIB and PI

conﬁrm these results with high accuracy [35,36]. Thus, the experimental ev-

idence supports a sublinear diﬀusion process as underlying the α-relaxation.

We remark that this result is in disagreement with assertions [19, 37], that

the stretched exponential relaxation function of the α-process originates from

heterogeneous motional processes, where polymer segments in diﬀerent parts

of the sample would relax at diﬀerent relaxation rates.

In the temperature range, where the α-relaxation is too slow to be ob-

served by neutron scattering, the β-process can be measured. The correspond-

ing spectra are a superposition of elastic and inelastic components indicative

of a localized motion.

Figure 13.12 displays this elastic part of the intensity, observed for PIB as

a function of Q [31]. The data were corrected for multiple scattering and ﬁtted

with the elastic incoherent structure factor (EISF) for a jump process between

two sites. The EISF is the Fourier transform of the self-correlation function

in the limit of inﬁnite times and reveals the asymptotic proton distribution

(see also (3.18), Chap. 3). The ﬁt reveals the jump distance d =0.27 nm. For

comparison the solid line displays the prediction for methyl group rotation,

which was invoked earlier on the basis of NMR experiments [38]. Within a

factor of two the time scale obtained from the neutron results agrees with that

from dielectric spectroscopy. Since the underlying process has an amplitude

of 0.27 nm and is also dielectrically active, it cannot be understood as due to a

methylgroup rotation alone. A possible interpretation is a combined backbone

and methyl motion, which is also supported by simulation results [39].

Let us draw a ﬁrst conclusion: Exploiting the Q-dependence of the co-

herent dynamic structure factor, which is accessed by NSE, at temperatures

below the merging temperature T

spatial information on the chain motions