Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

13 Viscoelasticity and Microscopic Motion in Dense Polymer Systems 529

KWW

[ (ns) ]



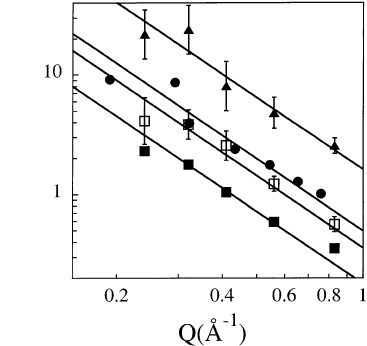
Fig. 13.11. Momentum transfer dependence of the characteristic time of the α-

relaxation for the polymers investigated: PVE at 340 K (), PIB at 365 K (•), PB at

280 K () and PI at 340 K (): (τ

KWW

)

as a function of Q in a double logarithmic

plot. Solid lines represent the Q-dependence expected in the homogenous scenario

[τ

KWW

]

∼ Q

behind the β-relaxation was obtained. The results suggest intrachain mo-

tions like rotations of the chain building blocks (cis and trans units) within

one chain. At temperatures around and above T

the NSE results qualiﬁed

the α-relaxation as being mainly related to interchain motions. The dynamic

structure factor, thereby, can consistently be described assuming that α-and

β-relaxations in 1,4 PB are statistically independent processes.

The self-correlation function measured on protonated samples reveals the

mean squared displacement of the moving hydrogens. The Q-dependence

of the characteristic relaxation time shows that motions underlying the

α-relaxation at least on a time scale larger than that of the dielectric

α-relaxation (corresponding to typically τ

KWW

−1

)) are following a

Gaussian process and are homogenous in nature.

13.4 Entropic Forces – The Rouse Model

We now turn to longer length scales, where motions resulting from local

chain potentials have already taken place, assume that the chains do not

interfere with each other in their motion and consider a Gaussian chain in a

heat bath as the simplest model for chain relaxation. The elements of such

a Gaussian chain are the so-called Kuhn segments, which consist of a few

monomers, so that their end-to-end distance follows a Gaussian distribution.

Their conformations are described by vectors a

along the chain. The chain

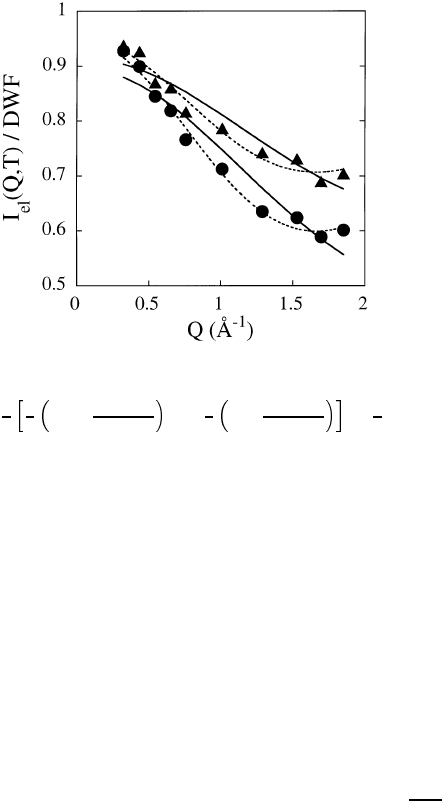
530 Dieter Richter

Fig. 13.12. Elastic incoherent intensities from PIB at 260 K () and 280 K

(•). The solid lines represent the prediction for methyl group rotation I

1+2

sin Qr

+ A

1 −

sin Qr

with r

=0.178 nm and A re-

lates to the jump time distribution function (see [4]). The dashed line gives the ﬁt

result for a two-site jump model with d =0.27 nm.

is then described by a sequence of freely connected segments of length .We

are interested in the motion of these segments on a length scale <r<R

This motion is described by a Langevin equation

+ ∇

· F {a

} = f

(t) (13.13)

where ζ

is the friction coeﬃcient, f

the stochastic force acting on the

segment n of extension a

and F the free energy. For segment motion,

the force ∇

F {a

} is dominated by the entropic part of the free energy

(S = k ln Prob{a

}), where

Prob{ a

}∼

i=1

exp



−

2



(13.14)

is the probability of a chain conformation {a

}. We ascertain that the re-

sultant entropic force is a special property of macromolecular systems with

a large number of internal degrees of freedom. This conformational entropy

generates the force stabilizing the most probable conformation. As already

mentioned above, it is also the basis for rubber elasticity.

The Rouse equation of motion (cf. (13.13)) is solved by a spectrum of

normal modes. These solutions are similar to the transverse vibrational modes

of a linear chain except that relaxations are involved instead of periodic

vibrations. We obtain for the relaxation rates

13 Viscoelasticity and Microscopic Motion in Dense Polymer Systems 531

3π



(13.15)

where N denotes the chain length. The mode index p counts the number

of nodes along the chain. The relaxation rate is proportional to the number

of nodes to the second power. On the basis of these normal modes we can

calculate the dynamic structure factor S(Q, t). This will be done later on.

Here, an asymptotic solution for long chains will be brieﬂy dealt with. It was

formulated by de Gennes [40], who ﬁnds for the characteristic relaxation rate

Ω

Ω =



. (13.16)

Unlike diﬀusion, where the characteristic relaxation rate is proportional to

the momentum transfer Q

, the fourth power is found here. Another char-

acteristic quantity of diﬀusive motions is the mean square displacement of a

segment. For Rouse motion follows

(r(0) − r(t))

∼t

1/2

(13.17)

which, again, is in clear contrast to normal diﬀusion where a linear time law

holds. In Fig. 10.19 of Chap. 10 patterns of PFG NMR results for polymer

diﬀusion are presented which follow the dependence of (13.17), though they

do not relate to Rouse motion. The Rouse equation (13.13) applies to a

length domain which is greater than the segment length and which is limited

upwards by the entanglement distance. In this domain, no further length

scale appears. The dynamic structure factor therefore assumes a scaling form

linking length and time scales.

S(Q, t)=f(Q



√

Wt) (13.18)

with the Rouse rate W =3k

T/(ζ

13.4.1 Neutron Spin-Echo Results in PDMS Melts

In order to study the Rouse dynamics, a polymer with a low plateau modu-

lus is needed, i.e. few entanglements and high ﬂexibility and mobility. Poly-

dimethylsiloxane (PDMS) fulﬁls these conditions. Neutron spin-echo exper-

iments were carried out for both the self-correlation function and the pair-

correlation function in PDMS melts.

Neutron measurements of the self-correlation function are normally per-

formed on protonated materials since then the incoherent scattering is

strongly dominating. Due to spin ﬂip scattering, which leads to a loss of

polarization, this approach is diﬃcult for the NSE method. In order to avoid

this obstacle, high-molecular-weight deuterated PDMS containing short pro-

tonated labels at random positions was synthesized. Each of these protonated

sequences contained eight monomers. In such a specimen, scattering is mainly

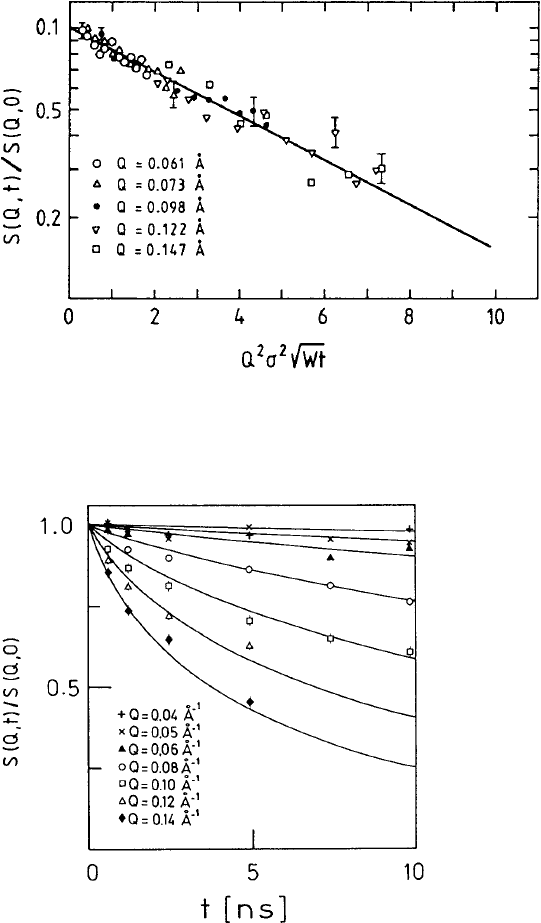
532 Dieter Richter

Fig. 13.13. NSE spectra for the self-correlation function measured in a randomly

labelled PDMS melt at 100

◦

C. The data are scaled with the Rouse variable (σ

≡

). The solid line is the result of a ﬁt with the Rouse self-correlation function.

Fig. 13.14. NSE spectra for the pair-correlation function in PDMS melts at 200

◦

The solid lines are the result of a ﬁt with the coherent structure factor calculated

by de Gennes (see text).

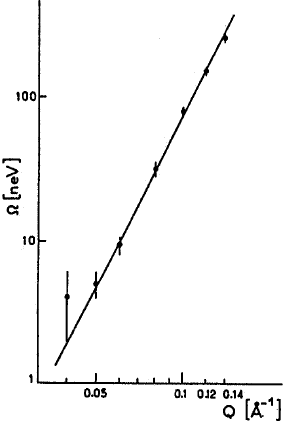
13 Viscoelasticity and Microscopic Motion in Dense Polymer Systems 533

Fig. 13.15. Dependence of the charac-

teristic relaxation rate Ω as a function

of the momentum transfer Q resulting

from an analysis of the spectra shown

in Fig. 13.14. The solid lines denotes the

predicted Ω ∼ Q

dependence.

caused by the contrast between the protonated sequence and the deuterated

environment and is therefore coherent. On the other hand, the sequences are

randomly distributed, so that there is no constructive interference of par-

tial waves from diﬀerent sequences. The scattering experiment measures the

self-correlation function under these conditions [5].

In Fig. 13.13 the scattering data are plotted versus the scaling variable of

the Rouse model (cf. (13.18)). The results for diﬀerent momentum transfers

follow a common straight line. For the case of the self-correlation function, the

scattering function directly measures the mean square displacement which,

according to (13.17), follows a square root law in time. This behaviour can be

directly read from Fig. 13.13 (For data from polyethylene propylene (PEP)

see also [41]).

The pair-correlation function for segment dynamics of a chain is observed

if some protonated chains are dissolved in a deuterated matrix. The scat-

tering experiment then observes the result of the interfering partial waves

originating from such a chain (cf. (13.1)). Figure 13.14 presents the dynamic

structure factor of a deuterated melt with 5% protonated chains. The solid

lines represent a ﬁt with (13.18) [12]. Obviously, the structure factor calcu-

lated by de Gennes satisfactorily describes the neutron data (the only ﬁt

parameter W

=3k

T

/ζ

). Figure 13.15 presents the characteristic relax-

ation rate Ω as a function of momentum transfer Q. The data are in very

good agreement with the predicted Q

law.

The microscopic Rouse relaxation rate W also determines the viscosity of

the non-entangled melt

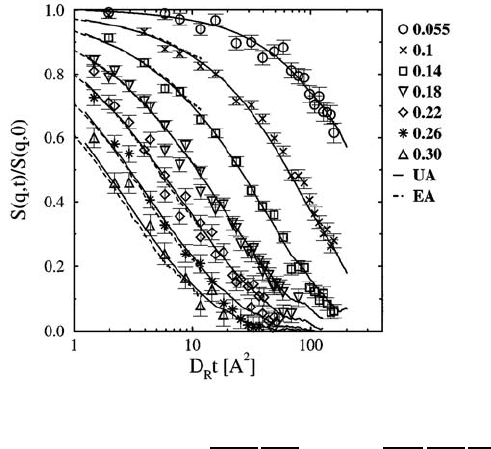
534 Dieter Richter

Fig. 13.16. NSE data

from PE melts vs.

computer simulations

using the EA and UA

models for diﬀerent

Q(≡ q)values/

−1

η =

ρN



ρN

(13.19)

where ρ is the polymer density and N

the Avogadro constant. Measured

viscosities and calculated viscosities using the microscopically determined

rate W are in agreement within 20%.

13.4.2 Computer Simulations

In order to learn about the limits of the Rouse model, recently a detailed

quantitative comparison of molecular dynamics (MD, cf. also Chap. 23) com-

puter simulations on a 100 C-atom polyethylene chain (PE) with NSE exper-

iments on PE chains of similar molecular weight has been performed [17].

Both the experiment and the simulation were carried out at T = 509 K. Sim-

ulations were undertaken for an explicit (EA) as well as for a united (UA)

atom model. In the latter the H atoms are not explicitly taken into account

but reinserted when calculating the dynamic structure factor. The potential

parameters for the MD simulation were either based on quantum chemical

calculations or taken from literature. No adjusting parameter was introduced.

Figure 13.16 compares the results from the MD-simulation (solid and broken

lines) with the NSE spectra. In order to correct for the slightly diﬀerent over-

all time scales of experiment and simulation, the time axis is scaled with the

center-of-mass diﬀusion coeﬃcient. From Fig. 13.16 quantitative agreement

between both results is evident.

Figure 13.17 compares the same experimental data, which agreed quan-

titatively with the simulations, with a best ﬁt to the Rouse model (see [17]).

Here a good description is observed for small Q-values (Q ≤ 0.14

−1

), while

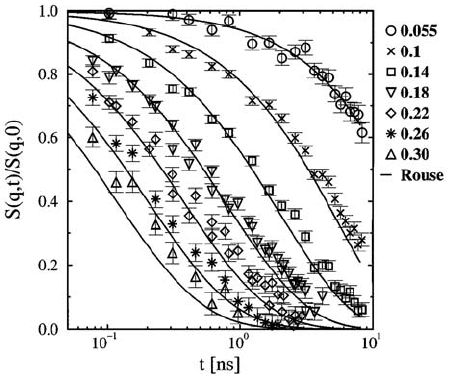
13 Viscoelasticity and Microscopic Motion in Dense Polymer Systems 535

Fig. 13.17. NSE

data from PE melts

in comparison to a

best ﬁt with the Rouse

model for diﬀerent

Q(≡ q)values/

−1

at higher Q important deviations appear. Similarly also the simulations can-

not be ﬁt in detail with a Rouse structure factor.

Having obtained very good agreement between experiment and simula-

tion, the simulations which contain complete information about the atomic

trajectories may be further exploited, in order to rationalize the origin for

the discrepancies with the Rouse model. A number of deviations evolve.

1. According to the Rouse model the mode correlators should decay in a

single-exponential fashion. A direct evaluation from the atomic trajec-

tories shows that the 3 contributing Rouse modes decay with stretched

exponentials displaying stretching exponents β of (0.96 (mode 1) and 0.86

(modes 2 and 3)).

2. A detailed scrutiny of the Gaussian assumption reveals that for t<τ

deviations occur.

3. While the Rouse model predicts a linear time evolution of the mean

squared centre of mass coordinate, within the time window of the simu-

lation (t<9 ns) a sublinear diﬀusion in form of a stretched exponential

with a stretching exponent of β =0.83 is found. A detailed inspection of

the time-dependent mean squared amplitudes reveals that the sublinear

diﬀusion mainly originates from motions at short times t<τ

=2ns.

The prediction of a time-dependent center-of-mass diﬀusion coeﬃcient has

recently been corroborated by NSE-experiments on short-chain polybutadi-

enes [42]. Figure 13.18 displays the mean squared center-of-mass displacement

from simulation compared to the same quantity obtained from the dynamic

structure factor at various Q-values. Both the simulation and the experimen-

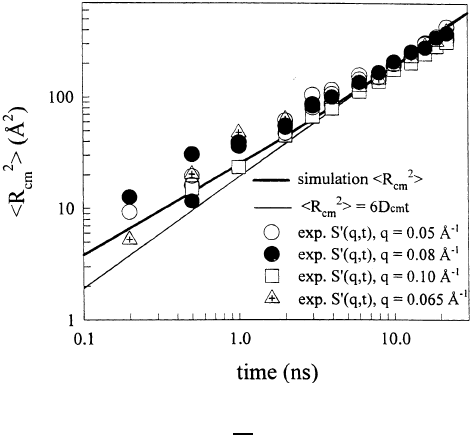
536 Dieter Richter

Fig. 13.18. Mean square center-of-mass displacement for PB chains in the melt

obtained from r

(t) = −

nS(Q, t). Solid line: simulation result; thin line

r

(t) = D

tal data consistently lead to a weaker than linear time dependence of the

center-of-mass displacement.

The overall picture emerging from this combined simulational and experi-

mental eﬀort is, that for chains, which should be ideal Rouse chains, the model

is capable of quantitatively describing the behaviour only on time scales of

the order of the Rouse time or larger and therefore on length scales of the

order of the radius of gyration of the chains or larger and in the regime, where

the chains actually show Fickian diﬀusion. The self-diﬀusion behaviour for

times smaller than the Rouse time and the relaxation of the internal modes of

the chains show small but systematic deviations from the Rouse prediction.

The origin of these discrepancies are traced to interchain interactions. On

the other hand, we will see that deviations observed at higher Q relate to

intrachain potentials.

Let us draw a second conclusion: The chain dynamics for times, where en-

tanglement eﬀects do not yet play a role, is excellently described by Langevin

dynamics with entropic restoring forces. The Rouse model nearly quantita-

tively describes (i) the Q-dependence of the characteristic relaxation rate,

(ii) the spectral form of both the self- and the pair-correlation function and

(iii) establishes the correct relation to macroscopic viscosity. (iv) Finally, de-

tailed comparisons with MD-simulation reveal small deviations originating

from interchain interactions.

13 Viscoelasticity and Microscopic Motion in Dense Polymer Systems 537

13.5 Long-Chains Reptation

13.5.1 Theoretical Concepts

The reptation model of de Gennes [43], Doi and Edwards [44] proceeds on the

intuitive assumption that the motions of a chain in a melt are signiﬁcantly

impeded by the surrounding chains in directions lateral to its own proﬁle. The

dominant diﬀusive motion, therefore, proceeds along the coarse-grained chain

proﬁle. A chain meanders through a melt like a snake. The lateral restrictions

are modelled by a tube running parallel to the coarse-grained chain proﬁle.

Its diameter is correlated with the plateau modulus of the melt, as discussed

in the introduction. The restriction of motion by other chains is not eﬀective

on the monomer scale, but permits lateral motions on intermediary length

scales (d

∼

=50...100

A). In this simple intuitive model, the experimental

observations for viscosity and diﬀusion can be readily made comprehensible.

According to (13.19) the viscosity is determined by the longest relaxation

time – here the abandonment of an initial conﬁguration. Assuming that the

chain is subject to a Rouse diﬀusion within its tube, D

∝ 1/N holds for the

tube diﬀusion. The chain has left an initial conﬁguration when it is diﬀused

over a contour length L = N .Thisgives

∝

∝ N

∝ η. (13.20)

In space, the contour of the chain follows a Gaussian random path, i.e. the

chain diﬀuses over a spatial distance during the time τ

, which corresponds

to its end-to-end distance (R

∝ N

1/2

). The reptation diﬀusion coeﬃcient

then reads

rep

∝

. (13.21)

Whereas the experimentally observed viscosity generally depends on the

molecular weight with an exponent slightly greater than 3 – there is rea-

son to suppose that an N

law is fulﬁlled for very long chain lengths – the

predicted chain length dependence of the diﬀusion coeﬃcient is directly con-

ﬁrmed experimentally.

What are the consequences of the localization tube for the dynamic struc-

ture factor? For short times during which the mean squared segment displace-

ment is smaller than the tube limitation, the chain motion should proceed

without being aﬀected by the tube restriction. In this case, the Rouse law

should apply, especially its scaling property of momentum transfer and time

(cf. (13.18)). For medium times, density ﬂuctuations transversely to the tube

have already equilibrated. Pair correlations along the tube are stabilized by

the localization tube and are only decomposed when the chain leaves the

tube. We thus expect that the dynamic structure factor tends to a constant

dependent on Q. A further decomposition of S(Q, t) only occurs for times

538 Dieter Richter

of the order of τ

. The value of the Q-dependent plateau results from the

Fourier transform of the localization tube. The essential new feature in the

dynamic structure factor of the reptating chain is the appearance of a length

scale d, which invalidates the scaling property of the Rouse model.

Quantiﬁcation requires analytical models, which can be compared with

the data. We would like to brieﬂy discuss three diﬀerent model categories

without explaining them in detail. (i) In so-called generalized Rouse models

[45, 46] the eﬀect of the topological constraints is described by a memory

function. In the limiting case of long chains, in the time domain of the NSE

experiment the dynamic structure factor can be explicitly calculated in such

models. (ii) Neglecting the initial Rouse motion for small values of the Rouse

scaling variable in his local reptation model de Gennes explicitly calculated

the collective chain motion in the localization tube [47]. For the dynamic

structure factor in the limit of long times, this gives

S(Q, t)



t→∞

= S(Qd

; Q

1/2

)



t→∞

=1−

. (13.22)

(iii) Des Cloizeaux ﬁnally formulated a rubber-like model for the chain motion

for intermediate times [48]. He assumed that for intermediate times the en-

tanglement points of the chains are ﬁxed in space and that the chains perform

Rouse motions under the boundary condition of ﬁxed entanglement points.

This rubber-like model is closest to the concept of a temporary network.

13.5.2 Experimental Observations of Chain Conﬁnement

Figure 13.19 compares the dynamic structure factors from polyethylene

melts, both taken at 509 K for two diﬀerent molecular weights [7, 8, 16, 23].

Figure 13.19a displays the structure factor for a short-chain melt (M

2000 g/mol). The solid lines display a ﬁt with the Rouse dynamic structure

factor. Very good agreement is achieved. Figure 13.19b displays similar re-

sults from a PE melt with a molecular weight of M

= 12400 g/mol. The

solid lines present the predictions of the Rouse model. While for the short-

chain melts this model describes well the experimental observations, for the

longer chains the model fails completely. Only in the short-time regime the

initial decay of the dynamic structure factor is depicted, while for longer

times the relaxation behaviour is strongly retarded signifying conﬁnement

eﬀects. In Fig. 13.20 the data from a M

= 36000 PE-melt at 509 K are

plotted as a function of the scaling variable of the Rouse model (see (13.18)).

In contrast to Fig. 13.13 the scaled data do not follow a common curve, but

after an initial common course they rather split into Q-dependent branches.

This splitting is a consequence of a dynamic length scale present in the melt,

which invalidates the Rouse scaling properties. We note, that this length is

of purely dynamical character and cannot be observed in static experiments.

Figure 13.21 presents recent experimental results on a polyethylene melt

= 190000), which were carried over a time regime of 170 ns [23]. The data