Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

5 Diﬀusion in Oxides 231

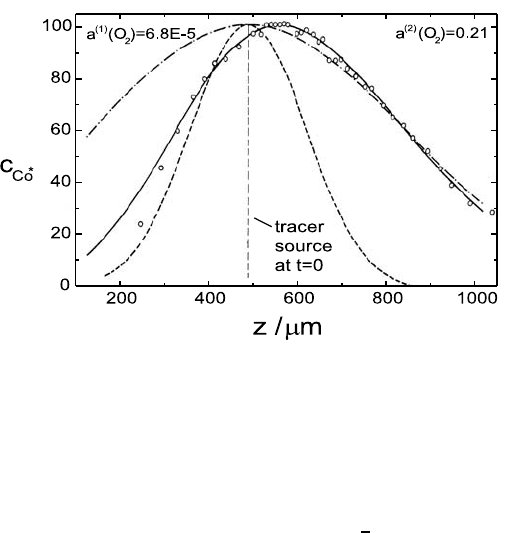
Fig. 5.12. Normalised tracer concentration proﬁle of

Co in CoO in an oxygen

potential gradient (T = 1210

◦

C, a

(1)

=6.8 · 10

−5

, a

(2)

=0.21, ∆z = 1184 µm,

t = 15 h) [20]. ◦ experimental concentrations; — best ﬁt using (5.37); – – – Gaussian

proﬁle for a homogeneous crystal at a

(1)

;–·– Gaussian proﬁle for a homogeneous

crystal at a

(2)

max

(t) − z

marker



D −

· f

· D



· b · t. (5.38)

Figure 5.12 shows a typical tracer concentration proﬁle of

Co in Co

1−δ

in an oxygen potential gradient. By ﬁtting of (5.37) the vacancy diﬀusion

coeﬃcient, D

, and the chemical diﬀusion coeﬃcient,

D,canbedetermined

simultaneously. Using (5.31) the average excess charge of the cation vacan-

cies was found to be α =0.86 [20]. This value is in reasonable agreement

with values calculated on the basis of equilibrium constants (see Sect. 5.2.1).

For comparison, the Gaussian proﬁles which one would obtain in a homoge-

neous crystal equilibrated at oxygen activities a

(1)

and a

(2)

are also shown in

Fig. 5.12. The actual proﬁle lies between the two Gaussian proﬁles.

Similar experiments have been performed for tracer diﬀusion of Fe in

magnetite, Fe

, which was exposed to an oxygen potential gradient [54].

Due to the high electronic disorder in magnetite (Fe

and Fe

ions are

regular structure elements) the chemical diﬀusion coeﬃcient,

D,isidentical

to the vacancy diﬀusion coeﬃcient, D

, in the vacancy regime, and identical

to the interstitial diﬀusion coeﬃcient, D

, in the interstitial regime [20]. This

means, that the two parameters which can be determined simultaneously

are the self-diﬀusion coeﬃcient of the dominating defect and the correlation

factor for tracer diﬀusion via this defect. In contrast to oxides with the NaCl-

structure, e.g. CoO, the eﬀective correlation factor for a jump sequence in the

spinel Fe

cannot be speciﬁed a priori since several vacancy and interstitial

or interstitialcy mechanisms are possible in magnetite. This is due to the fact

232 Manfred Martin

that in the spinel structure two regular cation sites exist, an octahedrally

and a tetrahedrally coordinated site. Likewise, several interstitial positions

are possible.

In the vacancy regime, three basic vacancy mechanisms are discussed.

They are characterised by jumps only within the octahedral sublattice, only

within the tetetrahedral sublattice [55], or jumps between these two sub-

lattices [56]. The geometrical correlation factors for these mechanisms are

=0.50, f

=0.56, and f

=0.73, respectively. The correlation fac-

tor obtained from tracer experiments in an oxygen potential gradient is

=0.56±0.07 [54] indicating preferred diﬀusion of Fe within the octahedral

sublattice, in agreement with results of in situ M¨oßbauer spectroscopy [56].

In the interstitial regime, the correlation factor obtained from tracer ex-

periments in an oxygen potential gradient is f

=0.43 ± 0.1. Only a direct

interstitial mechanism (f

= 1) can be excluded. The experimental accu-

racy is, however, too small to distinguish between diﬀerent interstitial or

interstitialcy mechanisms for which the theoretical correlation factors, f

,are

between0and1[55].

Impurity Diﬀusion in an Oxygen Potential Gradient

The ﬂux of impurity ions, B, in an oxide which is exposed to an oxygen

potential gradient consists also of two parts: a pure, diﬀusion term, which is

characterized by the impurity diﬀusion coeﬃcient, D

, and which describes

Brownian motion of the impurity ions, and a second part which is again a drift

term caused by the directed ﬂux of vacancies which drift through the oxide.

However, in contrast to self-diﬀusion, where the drift ﬂux was always opposite

to the vacancy ﬂux and directly proportional to the fraction of tracers, now

the magnitude and direction of the drift ﬂux have to be calculated with

the aid of linear transport theory. This means that transport coeﬃcients L

(i, j =A, B) have to be used which describe the coupled transport of A and

B under the inﬂuence of an applied oxygen potential gradient. The impurity

drift ﬂux was calculated in detail in [20] and can be written as

drift

= −j

· x

· β. (5.39)

As expected, the impurity drift ﬂux is proportional to the vacancy ﬂux, j

and the fraction of impurities, x

. In addition it is proportional to the ra-

tio of the diﬀusion coeﬃcients of the impurity, D

,andthesolvent,D

This ratio reﬂects the fact that impurities and solvent ions exchange with

diﬀerent rates with vacancies. As a result they are moved diﬀerently by the

vacancies. In contrast to these ﬁrst terms, which are model independent, the

last factor, β, depends on the microscopic model used. It describes essen-

tially the interaction of the impurity with its neighbours which can be small

(as is expected for homovalent impurities) or stronger (for aliovalent impuri-

ties). Particularly for higher valent impurities which possess a positive excess

5 Diﬀusion in Oxides 233

charge there can be strong interaction with the negatively charged vacancies.

Now the two possible limiting cases will be discussed: First, the situation

where the interaction is small. This means that impurities and vacancies

should drift in opposite directions, as in the case of self-diﬀusion. Second, the

case of attractive interaction between impurities and vacancies. Then impu-

rities and vacancies form bound pairs and the impurities should drift in the

same direction as the vacancies. This qualitative picture is conﬁrmed by the

theoretical results for the constant β in (5.39) which was calculated in [57]

within the ﬁve-frequency model. Within this model the transport coeﬃcients

(i, j =A, B) are known exactly [22]. The ﬁve-frequency model (Fig. 1.18,

note also footnote 15 in Chap. 1) is a nearest-neighbour model and uses ﬁve

exchange rates of vacancies and ions: ω

and ω

for exchange of vacancies

with solvent ions in the pure crystal (i.e. far away from the impurity) and

in the next neighbourhood of the impurity; ω

for vacancy jumps, which dis-

sociate an impurity-vacancy pair; ω

which creates a new pair; and ω

for

exchange of a vacancy and an impurity. For strong binding the parameter β

is negative, yielding an impurity drift ﬂux in the same direction as the vacan-

cies, while for weak binding β is positive, and the drift ﬂux is opposite to the

vacancies. Thus, an impurity drift experiment in an oxygen potential gradient

performed in the same way as described for tracer self-diﬀusion shows ﬁrst

bythedirectioninwhichtheproﬁlemoveswhetherstrongorweakimpurity-

vacancy binding prevails, and second allows the determination of ratios of

the exchange jump rates ω

(i =0, 1, 2, 3, 4).

An example is impurity diﬀusion of Fe in CoO in an oxygen potential

gradient. It was found, that the drift direction of the Fe-tracer proﬁle depends

on the oxygen potential region [19]. In region I (log a

≈−2) the proﬁle

drifts to the high oxygen potential side, i.e. opposite to the vacancies, while in

region II (log a

≈−8) the proﬁle shifts to the low oxygen potential side, i.e.

in the same direction as the vacancies. The impurity diﬀusion coeﬃcient, D

∗

and the constant β in (5.39) can be obtained from the proﬁles. To calculate

from these data the vacancy exchange rates ω

in the ﬁve-frequency model, or

at least ratios of them, two additional experimental parameters are needed.

These are: (i) the impurity correlation factor which was obtained from the

isotope eﬀect [58] and which changes from 0.78 in region I to 0.87 in region

II. (ii) the impurity-vacancy binding energy, ∆g

pair

, which was obtained from

the p

-dependence of the Fe-tracer diﬀusion coeﬃcient. It is small compared

to the thermal energy in region I and about 0.7 eV in region II [19]. All four

quantities are known exactly as functions of the ﬁve rates ω

(i =0,1,2,3,

4) within the ﬁve-frequency model [22]

. As a result four ratios of exchange

rates can be calculated in regions I and II, respectively:

The dependence of the impurity diﬀusion coeﬃcient and the impurity correlation

factor on the exchange ratees ω

can be found in Sect. 1.9.1 in Chap. 1, the

expression for β in [19], and the relation for the impurity-vacancy binding energy

is given by ω

/ω

=exp(−∆g

pair

T ).

234 Manfred Martin

region I: ω

/ω

=0.29, ω

/ω

=0.52, ω

/ω

=0.53, ω

/ω

∼

region II: ω

/ω

=0.02, ω

/ω

=0.14, ω

/ω

=0.60, ω

/ω

∼

= 300

While the ratios ω

/ω

and ω

/ω

remain nearly unchanged in passing

from region I to region II, ω

/ω

increases drastically and ω

/ω

decreases.

This is mainly due to the fact that the escape rate, ω

, decreases in pass-

ing from region I to region II indicating the transition from weak to strong

binding between Fe and vacancies. If the binding is mainly due to Coulom-

bic interaction between oppositely charged structure elements, one cause for

the change in ∆g

pair

could be the change in the relative concentrations of

the diﬀerently charged cation vacancies. At high oxygen activities (region I)

vacancies V



dominate, whereas vacancies V



become more important at

lower oxygen activities (region II). As a result, there is stronger Coulombic

interaction with trivalent iron at lower oxygen activities. On the other hand,

iron exists as Fe

and Fe

, and the fraction of trivalent iron decreases with

decreasing oxygen activity, which results in a smaller degree of association.

Another possible cause for the increase of ∆g

pair

goes back to the diﬀerent

sizes of di- and trivalent iron ions. The larger ionic radius of Fe

would

result in displacements of neighbouring ions which may be compensated by

association of a vacancy.

Demixing in an Oxygen Potential Gradient

If, instead of a pure oxide, a mixed oxide, (A

1−x

)O, in which oxygen is im-

mobile, is exposed to a stationary oxygen potential gradient, again diﬀerent

cation vacancy fractions are established at the high and low oxygen potential

sides. However, the resulting cation vacancy ﬂux from the high to the low

oxygen potential side causes ﬂuxes of both cations, A and B. In general, they

have diﬀerent mobilities and the oxide will become enriched in the more mo-

bile cation at the high oxygen potential side, while it will become enriched in

the less mobile cation at the low oxygen potential side (see Fig. 5.13). This

kinetic demixing process was studied ﬁrst by Schmalzried et al. [59,60] consid-

ering steady-state demixing and homovalent solid solutions, e.g. (Co,Mg)O,

where Co is the faster cation and becomes enriched at the high oxygen poten-

tial side of the oxide. The formal solution of the transient demixing problem

with moving boundaries and time-dependent boundary values can be found

in [61].

However, kinetic demixing may also be important in doped oxides

1−x

)O, where the kinetic segregation of impurities is of interest, e.g.

during sintering or alloy corrosion [62]. The basis for the subsequent analysis

is given by the general transport equations [44]

= −



·∇η

(5.40)

where L

are the transport coeﬃcients and η

is the electrochemical potential

(see Sect. 5.4). As shown in [63], in a dilute oxide, A

1−x

O(x  1)), the

5 Diﬀusion in Oxides 235

plow

phigh





(z)

0 zz

Fig. 5.13. Schematic representation of

the ﬂuxes of electron holes, cation va-

cancies and cations A and B, and the

initial and steady state concentration

proﬁle of A in a mixed oxide (A,B)O

exposed to an oxygen potential gradient

for the case that component A is faster

than B.

ﬂux of the dopant, B, can be written as

= −D

·∇c

− j



γ +



. (5.41)

The dimensionless quantity γ contains all physical correlation eﬀects and is of

the order of unity. Equation (5.41) shows that the dopant ﬂux consists of two

terms, a pure diﬀusion term, −D

∇c

, characterized by the dopant diﬀusion

coeﬃcient, D

(= L

RT/c

), and a drift term, which is proportional to

the vacancy ﬂux, j

. The direction of the drift term, which determines at

which side of the sample the dopant becomes enriched, depends crucially

on the sign and magnitude of the non-diagonal element L

.Particularlyin

trivalent doped oxides, AO(+B

), solute-vacancy interactions might result

in a non-vanishing cross term L

. Thus the demixing behaviour or the

kinetic segregation of the dopant B strongly depends on the strength of the

solute-vacancy binding energy.

Demixing experiments with Ga

-doped CoO [64] clearly show demix-

ing of Co and Ga with enrichment of Ga at the low oxygen potential side

(see Fig. 5.14). Since the tracer diﬀusion coeﬃcients of Co and Ga are also

known (see Sect. 5.3.1), the ratio L

GaCo

GaGa

can be obtained from the

demixing proﬁle using (5.41). The result is L

CoGa

GaGa

= −1.7, leading to

the following interpretation. Due to the strong binding between the dopant

Ga and the vacancies the drift ﬂux of the dopant is directed to the side of

lower oxygen potential (i.e. in the same direction as the vacancy ﬂux), where

the dopant Ga therefore becomes enriched. As shown in detail in [64] the

result L

CoGa

GaGa

= −1.7 can be explained adequately in terms of the

ﬁve-frequency model of impurity diﬀusion [22] and strong impurity-vacancy

binding, which was found independently in the tracer diﬀusion studies of this

system [21].

Finally it should be mentioned that demixing in an oxygen potential gra-

dient might be important also in oxygen ion conductors, such as yttria-doped

zirconia (YSZ) or doped lanthanum gallate (LSGM). When these oxides

are used as electrolytes, e.g. in solid oxide fuel cells (SOFCs), oxygen ions

are driven through the electrolyte and simultaneously electrons are ﬂowing

through the external circuit. As soon as the cations, e.g. Zr

and Y

236 Manfred Martin

Fig. 5.14. Demixing proﬁle of Ga in (Co

1−x

)O exposed to an oxygen potential

gradient (T = 1250

◦

C, a

(1)

=10

−6

(left), a

(2)

=10

−5

(right), ∆z = 725 µm,

=1.85%, t =38.5 h) [64].

YSZ, have diﬀerent diﬀusion coeﬃcients (see Sect. 5.3.2) there will be demix-

ing of the electrolyte. However, since cation diﬀusion is very slow, steady-

state demixing will be reached only after rather long times. If, for example,

the slowest diﬀusion coeﬃcient is taken as D =10

−18

−1

,oneobtains

15 000 years for an electrolyte thickness of 1mm. However, for a thickness of

10 µm the time to reach the steady state is only 1.5 years which is comparable

to the desired operating times of SOFCs.

5.5.2 Diﬀusion in an Electric Potential Gradient

In this section, electro-transport in oxides, i.e. the motion of ions due to an

external electric potential gradient, ∇Φ, will be discussed. As in the previous

section, where diﬀusion in an applied oxygen potential gradient was analyzed,

the ﬂuxes of the mobile components i (ions and electronic defects) can be

written as a sum of a diﬀusion and a drift ﬂux, j

= j

diﬀ

+ j

drift

.Ina

chemically homogeneous oxide without any gradients in chemical potentials,

the diﬀusion ﬂuxes vanish, and the drift ﬂux can be written as

drift

= −L



· F ·∇Φ. (5.42)

The sum in parentheses is usually denoted as eﬀective charge, z

i,eﬀ

.Itis

identical to the formal charge, z

, only if the cross coeﬃcients L

(i = k)are

zero and, consequently, the ﬂuxes are independent of each other

In metals, the eﬀective charge is frequently denoted by the symbol z

∗

5 Diﬀusion in Oxides 237

ext

sample

anode

tracer

cathode

Fig. 5.15. Schematic experimental

setup for the measurement of the ef-

fectivechargeinaconstantelectric

potential gradient (sandwich exper-

iment). The Gaussian curve shows

the broadening and shift of a tracer

concentration proﬁle which has de-

veloped from a point source located

originally in the middle of the crys-

tal.

The eﬀective charges are thus a measure of the cross coeﬃcients which are

again indicating defect-defect interactions. In homogeneous oxides exposed to

an electric ﬁeld, (radioactive) tracers can be used to measure the drift veloc-

ities of ions from which their eﬀective charges can be calculated (Sect. 5.5.2).

During demixing experiments, however, the oxide becomes chemically inho-

mogeneous resulting in drift and diﬀusion ﬂuxes as well. This situation will

be discussed in Sect. 5.5.2.

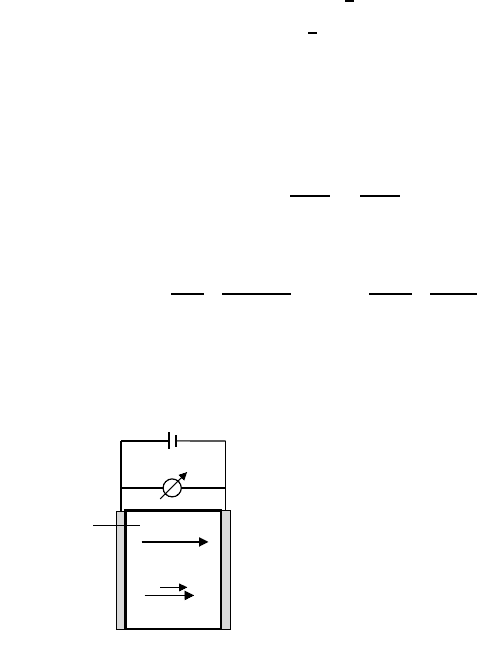
Tracer Diﬀusion in an Electric Potential Gradient

Figure 5.15 shows the typical experimental setup which can be used to mea-

sure the eﬀective charges, z

i,eﬀ

, of the host cation A or of impurity cations

B in an oxide AO using radioactive tracers, A

∗

and B

∗

. The tracer source is

located between two single crystals of the oxide in a sandwich arrangement,

and the electric potential gradient is applied by two reversible electrodes.

Diﬀusional broadening of the tracer source results in a Gaussian proﬁle from

which the tracer diﬀusion coeﬃcient can be obtained. Superimposed is a drift

of the tracer concentration proﬁle due to the applied electric ﬁeld. As shown

in detail in [18], the drift velocity of the tracer concentration proﬁle, v

drift

∗

drift

∗

, allows the determination of the eﬀective charges of the corresponding

cations, A or B. For self-diﬀusion, i.e. tracers A

∗

,weobtain

drift

∗

· z

A,eﬀ

· F ·∇Φ, z

A,eﬀ

= z

. (5.43)

The eﬀective charge of cation A, z

A,eﬀ

, contains the cross coeﬃcient, L

which indicates the ﬂux coupling between cations and electron holes. z

A,eﬀ

often called ‘charge of transport’. For impurity tracer cations, B

∗

,theresult

drift

∗

· z

B,eﬀ

· F ·∇Φ, z

B,eﬀ

= z

. (5.44)

TheeﬀectivechargeofB,z

B,eﬀ

, now contains two cross coeﬃcients, L

and

, which indicate ﬂux coupling between B and h and between B and A.

238 Manfred Martin

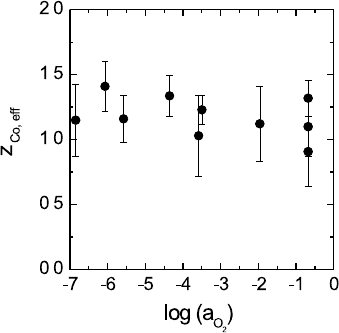
Fig. 5.16. Eﬀective charge of cobalt

in Co

1−δ

O as a function of the oxy-

gen activity at 1100

◦

C [18].

Figure 5.16 shows results for the charge of transport of Co in CoO as

a function of the oxygen partial pressure [18]. z

Co,eﬀ

has a value close to

+1.SincetheformalchargeofCoinCoOisz

= 2 this result demon-

strates clearly that the cross coeﬃcient L

Co h

is by no means negligible. The

cross eﬀect may be understood in terms of vacancy-electron hole associates,



•

 V



, and long-range Coulomb interactions between the oppo-

sitely charged vacancies and electron holes. Application of the Onsager-Fuoss

theory to this system [65] has shown that long-range interactions are of minor

signiﬁcance compared to association reactions. If the lifetime of the associate,



, is long enough to move as an entity, a simple interpretation of the ef-

fective charge can be given: in an electric ﬁeld, Co

ions move towards the

cathode via lattice site exchange with vacancies. If the vacancy is associ-

ated with an electron hole, two positive charges (ﬁxed on the cobalt ion)

movetowardsthecathodeand,atthesametime,onepositivecharge(the

hole associated with the vacancy) moves in the opposite direction during the

exchange step. Thus, the net charge which is moved towards the cathode

and which is the only quantity that can be measured is +1. Additional ev-

idence for vacancy-electron hole associates stems from measurements of the

electrical conductivity [66]. The data were modelled by two diﬀerent elec-

tronic conductivity processes, by means of free electron holes and by means

of electron holes bound by vacancies. The lifetime of a vacancy-electron hole

associate was found to be 20 times larger than the residence time of a free

electron hole on a cation site.

The eﬀective charges of the impurities indium and iron are shown in

Fig. 5.17. Whereas z

Fe,eﬀ

remains nearly constant with changing oxygen ac-

tivity with a value of about +1, z

In,eﬀ

decreases drastically with changing

and becomes even negative at a

< 10

−4

.Thisisequivalenttoare-

versal of the migration direction in the electric ﬁeld. In the range of high

5 Diﬀusion in Oxides 239

Fig. 5.17. Eﬀective charges of indium and iron in Co

1−δ

O as a function of the

oxygen activity at 1100

◦

C [18].

oxygen activities, the indium tracer moves towards the cathode, at low ac-

tivities it moves towards the anode, and therefore virtually behaves like an

anion. If we try to explain the observed behavior in the same way as for the

Co ions and assume that the impurity ions move via vacancy-electron hole

associates, V



(majority defects), we expect z

In,eﬀ

= +2 (with the formal

charge z

= +3) and z

Fe,eﬀ

=+2or+1(withz

= +3 or +2, respectively).

It is obvious from Fig. 5.17 that the strong decrease of z

In,eﬀ

and the ap-

pearance of negative values at low oxygen activities cannot be interpreted in

this manner. Furthermore, the experimentally obtained value of z

Fe,eﬀ

≈ +1

at high oxygen activities is unexpected, because iron should have a formal

charge of about +3 in this region. This means that in (5.44) the second ratio

including the cross coeﬃcient L

is also important. It is well known that

this cross coeﬃcient is due to the formation of impurity-vacancy pairs [22].

If the pair binding energy is strong enough to make the lifetime of the pair

much longer than the time required for an individual jump of the impurity

ion, the pair moves as an entity and the vacancy drags the impurity cation

towards the anode. As a result, we ﬁnd a negative eﬀective charge, as ob-

served experimentally. A more detailed formal analysis can be found in [67]

and [68].

240 Manfred Martin

Demixing in an Electric Potential Gradient

The external electric ﬁeld can also cause demixing of an initially homoge-

neous oxide solid solution, e.g. (A

1−x

)O, if the cations have diﬀerent mo-

bilities. In semiconducting oxides demixing due to an electric ﬁeld was found

by several authors [69–72]. Demixing processes have important practical im-

plications. Local composition changes can severely alter the physical, chem-

ical and electrical properties and are therefore a source of high temperature

degradation of materials in electric ﬁelds.

We consider a semiconducting, ternary oxide, (A

1−x

)

1−δ

O, with an im-

mobile oxygen sublattice, where the cations are mobile via a vacancy mech-

anism. As in the previous section, the external electric ﬁeld (see Fig. 5.18)

causes ﬂuxes of the homovalent cations, A

and B

, and electron holes,

•

, which are given by (5.40).

At the reversible electrodes the cations are involved in chemical reactions,

e.g. at the cathode:

+2e

−

(Pt) +

(g) → AO,

+2e

−

(g) → BO (5.45)

This means that the oxide grows at the cathode. At the anode the opposite

reactions take place, i.e. here the oxide dissociates into cations, electrons and

oxygen molecules. Thus, both oxide surfaces move to the cathode side. In the

steady state both surfaces and also both cations move with the same velocity,

v =

. (5.46)

Integration of (5.46) over the sample thickness yields

(1)

(2)

1 − x

(2)

1 − x

(1)

=exp



2FU

γ − 1



(5.47)

where x

(1)

and x

(2)

are the unknown molar fractions of A at the oxide sur-

faces and U is the applied voltage. γ = D

is a constant, since both

semiconducting

oxide

1-x

U=const.



(1) (2)

cathodeanode

Fig. 5.18. Schematic representation

of the ﬂuxes in a mixed oxide (A,B)O

exposed to an electric potential gra-

dient established by Pt-electodes.