Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models
Подождите немного. Документ загружается.

252 Franz Faupel and Klaus R¨atzke
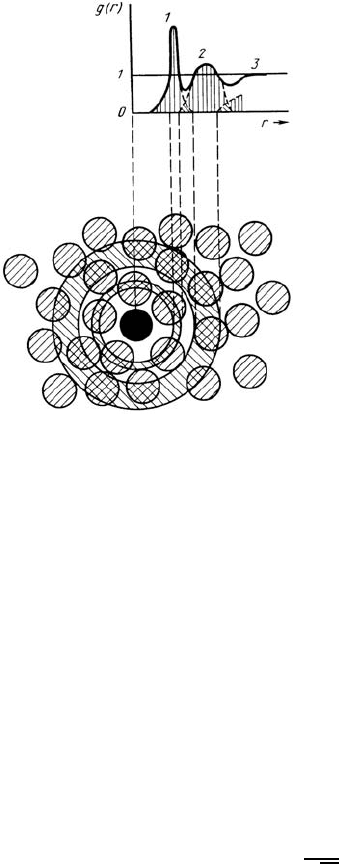
Fig. 6.1. Scheme of a monoatomic liq-
uid and the corresponding pair correlation
function g(r). Note the pronounced peak at
the nearest-neighbor distance r
1
.
methods [8], including neutron and x-ray techniques, M¨oßbauer spectroscopy,
and nuclear magnetic resonance, as well as from molecular dynamics calcu-
lations [9], that jumps of the size of lattice constants do not take place in
simple liquids. Diffusion rather proceeds continuously by frequent small mo-
tions. The atoms create their macroscopic displacement from a very large
number of collisions on a time scale of 10
−12
s, and the mean free path for
diffusion is at least one order of magnitude smaller than the atomic spacing.
Moreover, the pressure dependence of diffusion in liquids is much smaller than
predicted for a vacancy-like mechanism [7,10]. We shall see in Sect. 6.5.4 that
the pressure dependence of diffusion in some metallic glasses is not consistent
with a vacancy-like mechanism, either.
Apparently, transport in simple liquids such as metallic and van der Waals
liquids is much more gas-like than solid-like. Kinetic theories of self-diffusion
that are based upon the classical gas equation (6.1), Dulong Petit’s rule, and
geometrical arguments for the mean free path predict
D ∝
1
√
m
T
3/2
. (6.2)
Equation (6.2) reproduces the approximate temperature and pressure depen-
dence of D quite successfully in many simple liquids [7].
Molecular dynamics simulations [11] have confirmed a temperature depen-
dence D ∝ T
n
where n was found to be between 1.7 and 2.3. Such simulations
also allow one to investigate the time dependence of the mean square displace-
ment r
2
(t) on a microscopic level. A transition from gas-like ‘free flight’ for
very short times (t<10
−13
s) to Brownian displacement r
2
(t) =6Dt for
6 Diffusion in Metallic Glasses and Supercooled Melts 253
long times has been observed, which was also found experimentally, e.g.,
by neutron scattering [12]. In the transition interval many-body interactions
and memory effects play a role, and the motion of a given atom is correlated
with the motion of its neighbors. This collective behavior is the subject of
mode-coupling theories and becomes more pronounced in supercooled liquids,
where a dynamical glass transition is predicted at a critical temperature T
c
(see below).
High precision isotope-effect measurements of self diffusion in liquid Sn
under microgravity conditions [13] clearly show that cooperative effects sub-
stantially influence the diffusive motion of single atoms even at temperatures
well above the melting point (232
◦
C for Sn). At 800
◦
C an isotope effect of
E ≡ (D
α
/D
β
−1)/(
(
m
β
/m
α
−1) = 0.7 was found. It indicates only relatively
small deviations from ideal single-particle motion, which is characterized by
D ∝ m
−1/2
(see (6.2)) and E = 1. At 250
◦
C however, E drops to a value of
0.3, reflecting a high degree of collectivity. Here the mass effect is strongly
reduced by correlated motion of the tracer atom and surrounding particles.
The departure from gas-like uncorrelated binary collisions at low tempera-
tures is to be expected in view of the decrease of free volume. It is shown in
Sect. 6.5.3 that diffusion in structurally relaxed metallic glasses requires an
even higher degree of cooperativity, causing a very small isotope effect.
The concept of free volume results from a crude but physically plausible
approach. It has provided a deeper understanding of transport phenomena
and the liquid-to-glass transition. Free-volume models [14] have affinities with
kinetic theories and attribute most of the change in the diffusivity to ther-
mal expansion. But unlike simple kinetic theories diffusion is visualized as
a cooperative process. The basic assumption is that each molecule resides
within a ‘cage’ that is stable for times much longer than the vibration times.
A molecule is regarded as being able to move out of the ‘cage’ as soon as
random molecular movements produce a void, larger than some critical size
v
∗
, into which it can move, there being no energy barrier to the movement.
From this notion it is easy to show that the diffusion coefficient has the
form
D = D
0
exp
−
γv
∗
v
f
(6.3)
where the exponential term represents the probability that the redistribution
of free volume leads to fluctuations greater than v
∗
. v
f
is the mean free
volume per molecule, and γ is an overlap factor, typically between 0.5 and 1.
It considers that the same free volume is available to more than one molecule.
The temperature dependence of D is determined by v
f
(T ), whereas the pre-
exponential factor D
0
is a much weaker function of T . Cohen and Turnbull
[14] assumed that v
f
may be expressed approximately as
v
f
= αV (T − T
0
) . (6.4)
In this simple approach T
0
is the temperature at which the free volume dis-
appears, α and
V are the mean values of the coefficient of thermal expansion

254 Franz Faupel and Klaus R¨atzke
and the molecular volume over the temperature range of interest, respec-
tively. Although it is a weak point of the model that T
0
is found to be well
above absolute zero, (6.3) and (6.4) give a relatively good account of the
temperature dependence of D and of the viscosity (cf. Sect. 6.4) in many
liquids. An even better description has been obtained in a later development
of the theory by Cohen and Grest [15]. However, additional parameters were
introduced to describe v
f
(T ).
Free-volume models have also been applied extensively to transport in
polymers and also in metallic glasses (see Sect. 6.5).
In liquids the viscosity η is closely related to the diffusivity. Usually at
high temperatures the generalized Stokes-Einstein equation
D =
k
B
T
aη
(6.5)
is obeyed, where the parameter a is almost independent of T . The hydrody-
namic theory in the elementary Stokes-Einstein form, combining the theory of
Brownian motion (Λ
0
= D/k
B
T ) with Stokes law for the mobility Λ
0
of a big
spherical particle of diameter d in a continuous viscous fluid (Λ
0
=1/(3πdη)),
yields a =3πd. Various hydrodynamic theories are concerned with relation-
ships between η and D for more complicated cases, including non-spherical
molecules and concentrated solutions, where correlation effects, which are not
accounted for in Einstein’s expression of Λ
0
, come into play [8].
At high viscosities, for instance in supercooled liquids near the glass tran-
sition temperature, diffusion is eventually governed by activated hopping
mechanisms (Sect. 6.4). In this regime, as in crystalline solids, diffusion and
viscous flow are decoupled.
Several other theories have been developed for diffusion in ordinary liq-
uids, the discussion of which is beyond the scope of this chapter. The reader
is referred to reviews by Nachtrieb [16], Tyrell and Harris [8], Shimoji and
Itami [11], and DeBenedetti [17].
6.4 General Aspects of Mass Transport
and Relaxation in Supercooled Liquids and Glasses
In the foregoing section we have been concerned with molecular transport in
normal liquids at high temperatures under conditions of complete ergodicity.
Upon supercooling the viscosity increases markedly until at the so-called
glass-transition temperature macroscopic flow freezes in. Glasses exhibiting
this behavior are called ‘fragile’. By contrast, in some glasses termed ‘strong’
all physical properties change so gradually during cooling that no particular
temperature can be marked as border between the undercooled liquid and the
glass. Typical representatives of strong glasses are oxide glasses [18]. Fragile
behavior is observed in organic glasses and conventional metallic glasses. The

6 Diffusion in Metallic Glasses and Supercooled Melts 255
new bulk metallic glasses are significantly stronger than the conventionally
ones [1].
Every class of material can be transformed into an amorphous solid (with-
out crystallinity) if the experimental parameters are adjusted to the dynamics
of the system. While, e.g., quenching rates well above 10
10
K/s are required
for systems consisting of spherical molecules such as rare gases, many poly-
mers undergo always a glass transition on cooling. Generally, glasses are not
in a well defined metastable state after quenching, but exhibit irreversible re-
laxation processes, also referred to as ‘physical aging’ in polymers, which are
accompanied by annealing out of excess volume and changes in the chemical
short-range order.
T
g
is often somewhat arbitrarily defined as the temperature where η =
10
12
Pa s. This value corresponds to solid-like behavior on ordinary time scales
and results in T
g
values close to the caloric glass transition temperature
which is determined by the additional degrees of freedom above the glass
transition [19]. In the glassy state the temperature dependence of η follows an
Arrhenius law. Fragile glasses, particularly polymers and amorphous metals
generally obey the Vogel-Fulcher equation
η = η
0
exp
B
0
T − T
VF
(6.6)
in a certain temperature range near T
g
. η
0
, B
0
and the Vogel-Fulcher tem-
perature T
VF
are constant parameters. T
g
depends on the sample history, for
instance on the quenching rate. Equation (6.6) can be derived analogously to
(6.3). Within the free-volume concept, T
VF
is identical with the temperature
T
0
(see (6.4)) where v
f
vanishes. The functional form of the Vogel-Fulcher law
can also be shown to be a direct consequence of cooperativity in the move-
ment of the molecules [20] and can also be derived from the more advanced
mode coupling concept discussed below.
The glass-to-liquid transition is closely related to the relaxation of shear
stress and dielectric properties, for example. The corresponding relaxation
function Φ(t) for this so-called α relaxation can be described by an universal
empirical expression
Φ(t)=exp
!
−(t/τ)
β
"
. (6.7)
Here β is usually in the range between 0.3 and 0.7 depending on the material.
This ‘stretched exponential’ or Kohlrausch behavior [19] departs markedly
from simple Debye relaxation (β = 1), which is characterized by a thermally
activated process with a single activation energy. Φ(t)dropsmuchfaster
for short times and has a pronounced long time tail typical of transport
processes in disordered media (see below). The relaxation function Φ(t)obeys
a time-temperature scaling principle [21], i.e. relaxation functions measured
at different temperatures fall on a single ‘master curve’ Φ(t/τ(T )).
In addition to the slow α relaxation, which involves long range atomic
transport, there is a second fast process in amorphous media referred to as β
256 Franz Faupel and Klaus R¨atzke
relaxation. It can be associated with local rearrangements of molecules. The
time-temperature scaling obeys an Arrhenius law through the glass transi-
tion. At high temperatures the α relaxation becomes increasingly faster until
at a certain temperature above T
g
α and β relaxation coincide, i.e. β relax-
ation becomes part of the flow process. In polymers β relaxation has been
attributed to well defined local mechanisms like movements of chain seg-
ments or side chain rotations [22], but β relaxation has also been observed in
metallic glasses (see Sect. 6.5.1).
So far we have discussed theoretical descriptions of the glass transition
and the dynamics around T
g
that are related to a critical temperature below
T
g
, for example to T
VF
, and to a true thermodynamical transition. On the
other hand, recent mode coupling theories [23,24] predict a dynamical phase
transition at a critical temperature T
c
, well, typically 30–150 K, above T
g
.
They are based on the hydrodynamic theory of liquids. The classical the-
ory is linear, however, and is only valid exactly in the limit of long times
and wavelengths, whereas the glass transition is characterized by a freezing-
in of density fluctuations with finite wavelengths due to strong interactions
between the atoms or molecules in a liquid. Therefore, non-linear coupling
between density-density correlations, the relevant modes of the theory, are
introduced, and memory effects are taken into account.
Upon cooling a dense liquid the aforementioned (Sect. 6.3) cage effect,
viz. the trapping of molecules by surrounding particles, which induces time
dependent potential barriers, becomes more and more effective and may even-
tually, at a critical temperature T
c
, lead to a partial localization of molecules
or clusters of molecules in a metastable state. If activated hopping between
metastable states (jump diffusion) can be neglected, a sharp transition from
an ergodic to a non-ergodic state occurs. This transition is reflected in an al-
gebraic divergence of the viscosity at T
c
.BelowT
c
only local rearrangement of
molecules but no transport over macroscopic distances is possible. Real sys-
tems are always expected to return to ergodicity at sufficiently long times as a
consequence of hopping diffusion, not included in the original mode-coupling
theory.
The predictions of mode coupling theory have been tested in numerous
systems resulting in a qualitative and sometimes even quantitative agreement
of microscopic dynamics with the theory. For a review we refer to [24].
Recently, thermally activated hopping processes have been incorporated
into mode-coupling theories [25]. It has been shown [23] that the viscosity
may exhibit a Vogel-Fulcher-like dependence in a certain temperature range
below T
c
. In particular, the cross-over to an Arrhenius behavior that is ex-
perimentally observed at T
∼
= T
g
has been predicted for sufficiently strong
coupling [25]. In these terms the Arrhenius law η ∝ exp(H/k
B
T )resultsfrom
the dynamics of the β process. As mentioned earlier the β process reflects
the decay of local density fluctuations and does not freeze in below T
c
.Local
displacements, i.e. short wavelength clusters, induce a disturbance in the sur-
6 Diffusion in Metallic Glasses and Supercooled Melts 257
rounding medium that may give rise to rearrangements of long wavelengths
in a macroscopic volume and induce a feedback effect on the original cluster.
This may lead to a medium-assisted hopping process, caused by the nonlin-
ear coupling between longitudinal currents of quite different wavelengths but
identical time dependence, being governed by the dynamics of β relaxation
in the initial stage of the diffusion process. In this extended mode coupling
theory, transport in the glassy state is a highly cooperative process on all
length scales. We shall see in Sect. 6.5.3 that isotope effect measurements of
diffusion in a structurally relaxed metallic glass strongly support this view.
While atomic transport in glasses obviously proceeds via jump diffusion,
the disordered nature of these materials gives rise to further peculiarities that
are absent in crystalline solids. Apart from the difficulty in defining defects
like vacancies or interstitials, which are directly related to the existence of a
lattice and govern diffusion in crystals, activation barriers, site energies, and
jump distances exhibit a certain distribution around their average values.
Modeling of these phenomena in three dimensions requires drastic simplifi-
cations (see Chap. 18 and [26]). On the other hand, the salient features are
already revealed by a separate study of the different types of disorder and
under the assumption of a Gaussian distribution function.
Disorder in the jump distance only affects the pre-exponential factor D
0
(see Chap. 1) and usually does not induce a significant perturbation unless
the spectrum is very broad [27]. The effect of a random distribution of site
energies is illustrated in Fig. 6.2a. The diffusivity D is smaller than that for a
sharp site energy, and the apparent activation energy is larger because trap-
ping in the deep wells cannot be avoided. Conversely, randomness in the bar-
rier heights (Fig. 6.2b) enhances diffusion in three dimensions, where the high
barriers can be by-passed. Here D becomes time dependent. For short times
or high frequencies, i.e. short-range diffusion, the small activation enthalpies
essentially govern the diffusion behavior. Long-range diffusion, however, is
mainly controlled by the high barriers and, thus, proceeds slower.
In real glasses a combination of site and saddle point disorder is expected
(Fig. 6.2c). At high frequencies both effects cancel out, but for long times
the deep traps dominate. The deviations from crystal-like linear Arrhenius
behavior without frequency dependence go to zero for T →∞and are most
pronounced at low temperatures.
The time dependence of D causes anomalous diffusion on a certain time
or frequency scale where the mean square distance walked by the diffusing
particle increases sublinearly instead of linearly with time (see Chaps. 10, 18,
19). Disorder related anomalous diffusion is well known from ionic conduc-
tion in glasses (see Chaps. 20 and 21 and [28]) and has also been observed
for hydrogen in metallic glasses. At room temperature the range of strong
frequency dependence of the hydrogen mobility proved to be between 10
7
and 10
11
s
−1
[29].
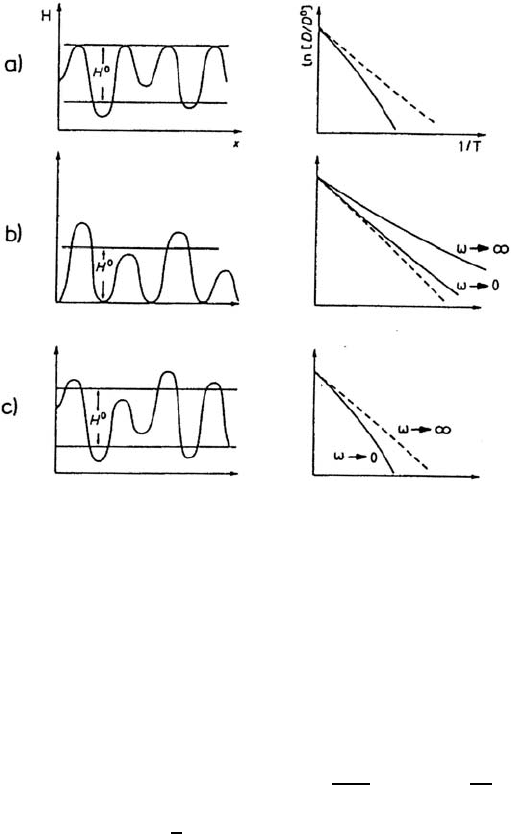
258 Franz Faupel and Klaus R¨atzke
Fig. 6.2. Effect of (a)siteand(b) barrier height disorder and (c) of their combi-
nation on diffusion in three dimensions (schematically). The straight dashed lines
in the Arrhenius plots represent the average activation energy H
0
. D
0
is the high-
temperature limit of the diffusivity D. The behavior at low and high frequencies, ω,
corresponding to long and short times, respectively, is indicated (after Kronm¨uller
et al. [30]).
Transport in disordered media with a Gaussian activation-energy distri-
bution around H
0
with variance σ leads to a characteristic temperature law
for the zero-frequency diffusion coefficient (long-time limit)
D(T,ω =0)=D
0
exp
−
H
0
k
B
T
exp
−
T
0
T
2
. (6.8)
Here k
B
T
0
= σ/
√
2(seee.g.Kronm¨uller and Frank [30]). For low tem-
peratures and/or large widths of the energy distribution one obtains an
exp[−(T
0
/T )
2
] variation with temperature. Equation (6.8) has been con-
firmed by Monte-Carlo simulations [31]. Moreover, B¨assler [32], reanalyzing
viscosity data of various supercooled liquids, has shown that η(T )ispro-
portional to exp[(T
0
/T )
2
] over ten decades in η and extending to the glass
transition. As expected, the concept fails at high temperatures where the
barriers can no longer be regarded as quasi-static.
In summary, there is ample evidence from experiment, theory, and com-
puter simulation that liquid-like diffusion has come to rest in glasses and
6 Diffusion in Metallic Glasses and Supercooled Melts 259
that transport is clearly of the jump type. The details of the diffusion mecha-
nisms, in particular the role of defects and the number of atoms or molecules
involved certainly depend on the material under consideration.
6.5 Diffusion in Metallic Glasses
6.5.1 Structure and Properties of Metallic Glasses
Metallic glasses of practical importance are always alloys of at least two
components because of the ease of crystallization of monoatomic systems
(Sect. 6.4). They can essentially be subdivided into two groups [33]: those of
the metal-metalloid type and those of the metal-metal type. In the first group
transition metals like Fe, Co, Ni, and Pd are alloyed with typically 15–20%
of metalloids, such as B, C, P, Si, and Ge. The second group often consists of
an early transition metal, e.g. Zr and Nb and a late one, for instance Co, Ni,
and Pd. Frequently, especially for technological applications, these elements
are used in multicomponent systems.
The structure of amorphous alloys, in particular the absence of extended
defects and the inherent free volume, gives rise to a variety of desirable prop-
erties and unique property combinations [34]. Metallic glasses can be very
ductile, for example, and still exhibit a high flow stress and fracture tough-
ness. The electrical resistivity is large and almost independent of temperature.
Magnetic glassy metals are generally characterized by excellent soft magnetic
properties. The new bulk metallic glasses can be produced at relatively low
cooling rates similar to processing of oxide glasses and hence offer additional
applications [35] such as the fabrication of very precise microcomponents, for
instance [36].
Various methods have been developed for the preparation of conventional
amorphous metals [37]. They can be quenched from the liquid state, e.g., by
melt spinning or splat quenching, and can be produced by vapor condensation
and sputter deposition. Moreover, it is possible to transform crystalline solids
into the amorphous state by solid-state reaction, ion implantation, neutron
irradiation, ball milling, high-pressure application, and other techniques [38].
As one would expect, there are close similarities between the structure of
glassy and liquid metals, which are also reflected in the pair-correlation func-
tion g(r) (Fig. 6.1). The maxima and minima are somewhat more pronounced
in amorphous metals and the second peak is split into two subpeaks. Since
g(r) is a one-dimensional representation of the unknown three dimensional
structure, further modelling is required to reveal the atom arrangement [39].
One approach is based on the dense random packing of hard spheres intro-
duced by Bernal [40]. Here the structure consists of a number of different
kinds of polyhedra, the majority of which are tetrahedra and octahedra.
This simple model already explains the main features in g(r) for metallic
glasses. The subpeaks of the second peak are attributed to atoms occupying
260 Franz Faupel and Klaus R¨atzke
the vertices of two tetrahedra having a common base and to three collinear
atoms, respectively. Major improvements have been attained by taking into
account chemical short-range order and by sequential computer relaxation of
soft spheres [39]. Recent molecular dynamics simulations are based on real-
istic interatomic potentials and benefit strongly from progress in computer
processing speed [41–43].
Chemical short-range order is a common characteristic of amorphous al-
loys. Partial pair correlation functions indicate that close contact between
metalloid atoms is very unlikely in metal-metalloid glasses [44]. In metal-
metal glasses atoms of the same kind are nearest neighbors, but nearest
neighborhoods between different components are more likely [44].
The pronounced chemical short-range order of most metallic glasses is
due to the fact that these systems tend to form strong compounds upon
crystallization. Therefore, Gaskell [45] modelled the amorphous structure as
a random network of unit cells of the nearest, in composition, crystalline
compounds.
Amorphous alloys have also been described in terms of icosahedral pack-
ing [46, 47]. In icosahedra, which consist of twenty slightly distorted tetra-
hedra, twelve atoms are grouped around a central atom. Their local fivefold
symmetry is broken up by a disordered entangled array of +72
◦
and −72
◦
disclination lines. The disclinations are associated with sixfold and fourfold
symmetries, respectively. They are forced in by ‘frustration’, viz. the incom-
patibility of flat space with a space-filling icosahedral crystal.
Most glass forming alloy systems are able to form glasses over an extended
composition range. In some cases discontinuities in physical properties are
observed, which have been related to structural changes [37]. For instance, a
transition from dense random packing to the formation of random networks
was proposed for Fe
1−x
B
x
at x =0.18. The above mentioned molecular
dynamics simulations have revealed more complex structural transitions in
metal-metal glasses [48].
Upon heat treatment amorphous alloys undergo rearrangement processes.
Structural relaxation and sometimes also phase separation, which are gener-
ally accompanied by drastic and detrimental changes in properties [49], may
occur already at temperatures well below T
g
. Phase separation, giving rise to
inhomogeneities on a scale of some 10 nm, appears to be closely related to the
changes in the glassy structure with composition, mentioned above [50,51].
Structural relaxation affects to a greater or lesser extent all physical prop-
erties, specifically structure sensitive quantities such as the viscosity and the
diffusion coefficient. Irreversible relaxation takes place when as-prepared sam-
ples are heated for the first time at elevated temperatures. On the time scale
of this process, there occur also much faster reversible relaxation processes,
which are superimposed on the irreversible background. The degree of irre-
versible relaxation appears to depend strongly on the rate of cooling during
preparation of the glass and is higher, e.g., for splat quenched than for melt
6 Diffusion in Metallic Glasses and Supercooled Melts 261
spun samples [52]. Irreversible relaxation is accompanied by an increase in
density of the order of 0.1% and a narrowing of the first peak in the pair cor-
relation function g(r). These effects have been interpreted as resulting from
an elimination of extremely short and long atom distances in the nearest-
neighbor shell of a given atom [53].
After extended isothermal structural relaxation metallic glasses are in a
metastable non-equilibrium state that can be described in terms of thermo-
dynamics of metastable systems [54]. This is also reflected in the course of η
and D as function of time. η was found to increase linearly with t during re-
laxation. Consequently, the relative increase d ln η/dt decreases continuously,
and the system has often been described to approach a so-called isocon-
figurational state after sufficiently long times [55]. The diffusion coefficient
drops initially and reaches a plateau value which is reproducible and constant
within experimental error as long as annealing is not performed at very long
times close to T
g
[56–58] (see also Fig. 6.6). Such conditions are excluded
in conventional metallic glasses due to the onset of crystallization. Recent
investigations on bulk metallic glasses have shown that the ‘plateau value’
is not constant and that complete relaxation from the frozen-in glassy non-
equilibrium state to the metastable equilibrium supercooled liquid state can
be achieved upon long-time relaxation [59, 60].
The mechanisms of structural relaxation are still discussed controversially,
though there is general agreement that the increase in density ρ and the
changes in g(r) involve the annealing of quenched-in excess volume. Accord-
ing to Egami [61], the large effect in η and the relatively small change in ρ
can be attributed to the mutual annihilation of regions of high positive and
negative atomic level stress. The movement of these ‘p and n defects’ involves
collective rearrangements of atoms. Within this concept the small increase
in ρ is caused by a second order effect that arises from the anharmonicity
of the interatomic potentials. Spaepen [62] has explained the increase in η
during structural relaxation within the free-volume model as resulting from
the bimolecular annihilation of frozen in free-volume fluctuations. There are
similarities between both models, in particular with regard to the internal an-
nihilation of frozen-in defects. Horv´ath et al. [56] have studied the relaxation
behavior of D. The time and temperature dependence could be described by
a single activation enthalpy. These authors came to the conclusion that re-
laxation takes place by annihilation of quenched-in ‘quasi-vacancies’ mainly
through migration to the outer surface. The quasi-vacancies are envisioned
as localized defects that are stable on the time scale of several atomic jumps.
We will come back to the mechanisms of structural relaxation in Sect. 6.5.5.
The role of defects, especially of thermal quasi-vacancies, in diffusion will
be discussed in the following sections. Unfortunately, positron annihilation,
which has been so successful in monitoring vacancies in crystals, does not
allow to identify unequivocally vacancy-like defects in metallic glasses because
of saturation trapping of the positrons at large interstices [63]. Computer
