Hearn E.J. Mechanics of Materials. Volume 1
Подождите немного. Документ загружается.


514.16
Complex Strain and the Elastic Constants
383
14.16.
Alternative representations
of
strain distributions at a point
Alternative forms of representation for the distribution of stress at a point were presented
The values of the direct strain
60
and shear strain
ye
for any inclined plane
8
are given by
in
413.7;
the directly equivalent representations for strain are given below.
equations
(14.14)
and
(14.15)
as
60
=
$(E,
+
E,)
++(E,
-
cy)
cos
28
+
f
y,,
sin
28
f
ye
=
-
[$(E,
-
E~)
sin
28
-
+
y,,
cos
281
Plotting these values for the uniaxial stress state on Cartesian axes yields the curves of
Fig.
14.23
which can then be compared directly to the equivalent stress distributions
of
Fig.
13.12.
Again the shear curves are "shifted by
45"
from the normal strain curves.
i"
I
I I
I
I
I
I
1
1
-8
0"
45O
90'
135"
180'
225O
270"
315'
360"
(X)
(Y)
(X)
(Y)
(XI
(P)
(q)
(P)
(q)
(PI
Fig.
14.23.
Cartesian plot
of
strain distribution at a point under uniaxial applied stress.
Comparison with Fig.
13.12
shows that the
normal
stress and shear stress curves are each in
phase with their respective normal strain and shear strain curves. Other relationships
between the shear strain and normal strain curves are identical to those listed on page
335
for
the normal stress and shear stress distributions.
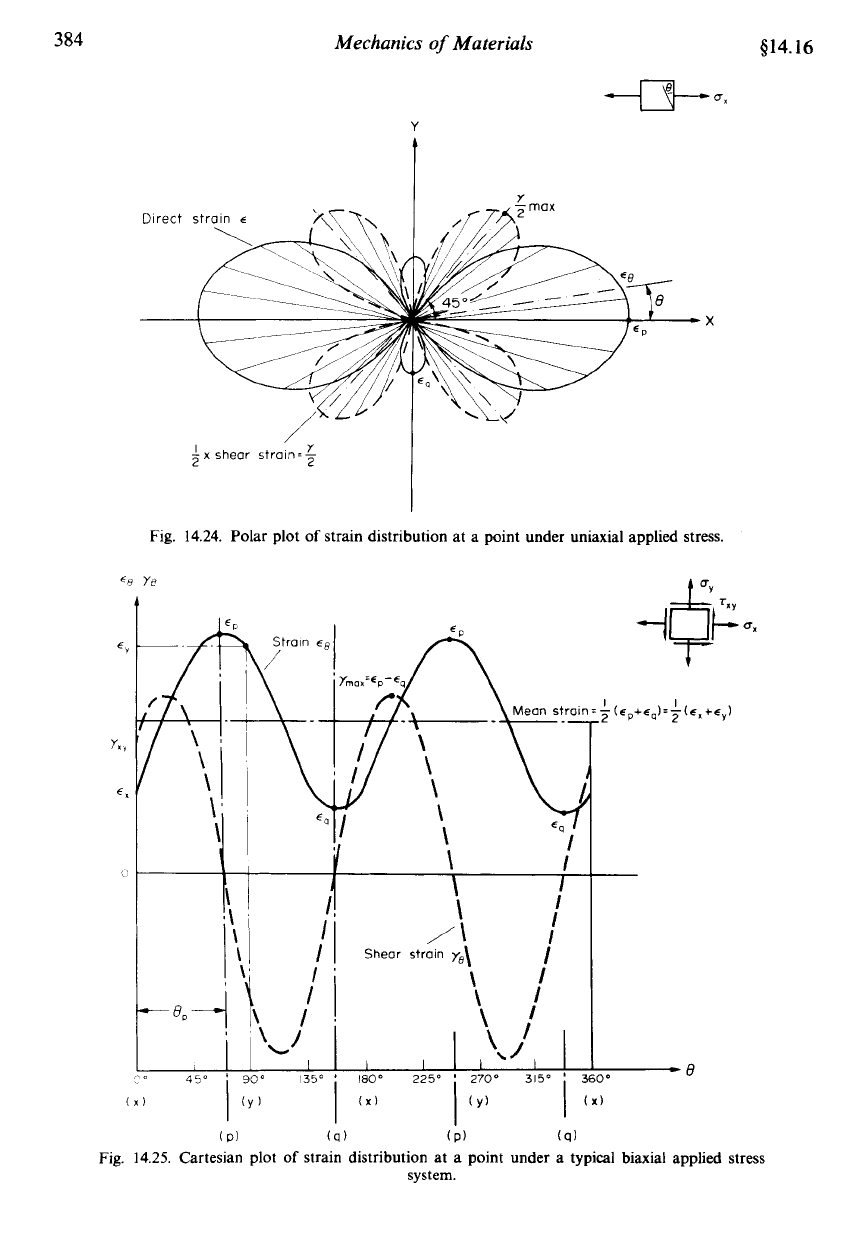
The alternative polar strain representation for the uniaxial stress system is shown in
Fig.
14.24
whilst the Cartesian and polar diagrams for the same biaxial stress systems used for
Figs.
13.14
and
13.15
are shown in Figs.
14.25
and
14.26.
384
Mechanics
of
Materials
414.16
X
__--
/
$
x
shear
strain=L
2
Fig. 14.24. Polar plot
of
strain distribution at a point under uniaxial applied stress.
Ye
(P)
(q)
(P)
(q)
Fig. 14.25. Cartesian plot
of
strain distribution
at
a point under a typical biaxial applied stress
system.
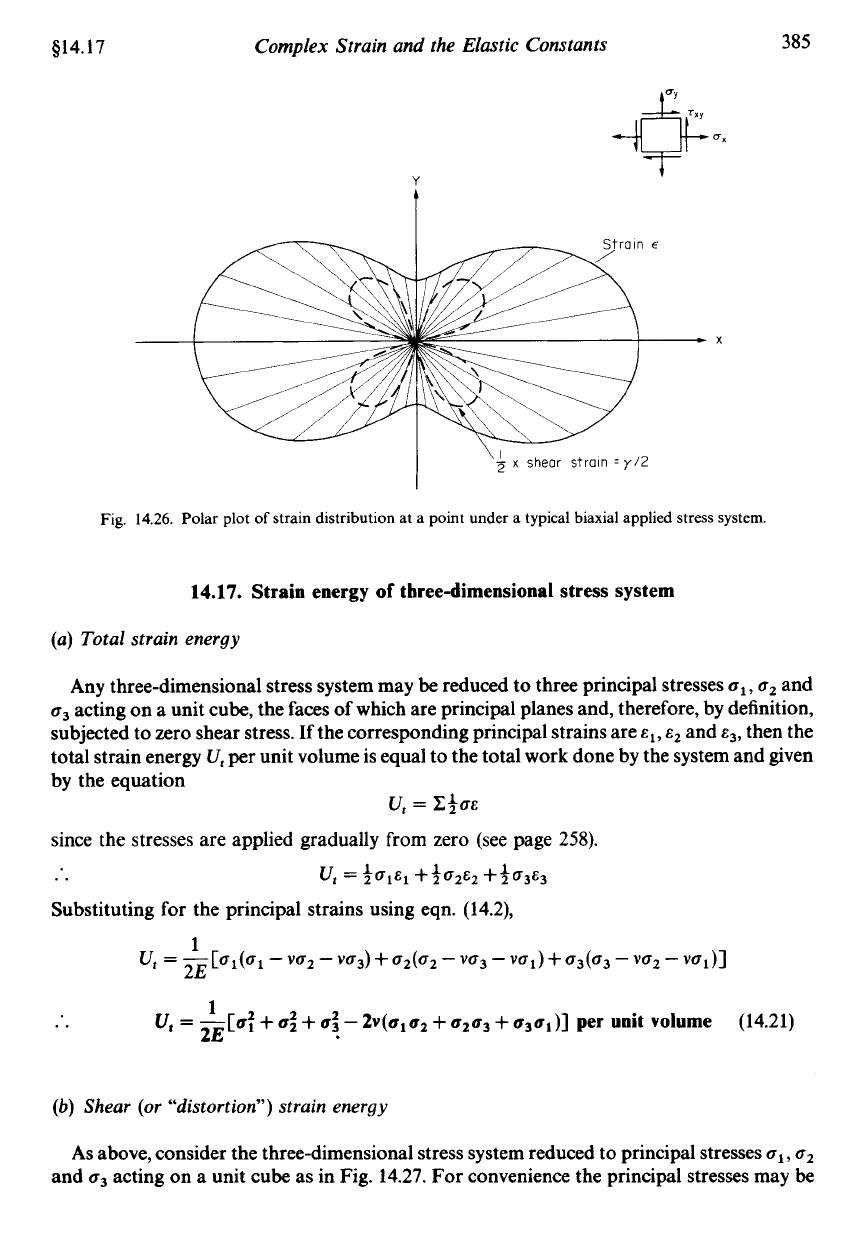
414.17
Complex Strain and the
Elastic
Constants
Y
4
385
Fig.
14.26.
Polar plot
of
strain distribution at a point under a typical biaxial applied stress system.
14.17.
Strain energy
of
three-dimensional stress system
(a) Total strain energy
Any three-dimensional stress system may be reduced to three principal stresses
cr,,
g2
and
o3
acting on a unit cube, the faces of which are principal planes and, therefore, by definition,
subjected to zero shear stress. If the corresponding principal strains are
E,,
e2
and
z3,
then the
total strain energy
U,
per unit volume is equal to the total work done by the system and given
by the equation
since the stresses are applied gradually from zero (see page
258).
ut
=
X+Q&
u,
=
~U,&,
++az&,
++a,&,
..
Substituting for the principal strains using eqn. (14.2),
1
2E
u,
=
-[Ca,(a,
-
vu2
-
V63)
+
oz(a2
-
VQ3
-
Vb,)
+
U3(Q3
-
va2
-Val)]
1
2E
v,
=
-[
a:
+
uf
+
ai
-
2v(o,a2
+
~2~3
+
a3al)]
per unit volume
(14.21)
..
(b)
Shear (or “distortion”) strain energy
As above, consider the three-dimensional stress system reduced
to
principal stresses
ol,
o2
and
o3
acting on
a
unit cube as in Fig. 14.27. For convenience the principal stresses may be

386
Mechanics
of
Materials
614.17
General stress state Hydrostcrtic stresses Deviatoric stresses
Fig.
14.27.
Resolution
of
general three-dimensional principal stress state into “hydrostatic” and
“deviatoric” components.
written in terms of a mean stress
5
=
+(a,
+
b2
+
u3)
and additional shear stress terms,
i.e.
6,
=
f(6,
+
62
+
63)
+
j(6,
-
62)
++(a,
-
63)
62
=
+(a,
+
62
+
63)
+$(a,
-
a,) +$(a2
-
63)
63
=
$(6,
+
62
+
63)
+
303
-
61)
++(a3
-
62)
The mean stress term may be considered as
a
hydrostatic
tensile stress, equal in
all
directions, the strains associated with this giving rise to no distortion, i.e. the unit cube under
the action of the hydrostatic stress alone would be strained into a cube. The hydrostatic
stresses are sometimes referred to as the
spherical
or
dilatational
stresses.
The strain energy associated with the hydrostatic stress is termed the
volumetric strain
energy
and is found by substituting
into eqn.
(14.21),
i.e.
61
=
02
=
03
=
+(a,+
02
+
63)
volumetric strain energy
=
-
2E [(“1+y+03)i](l-2v)
(1
-
2v)
..
U”
=
___
[
(al
+
u2
+
a3)’]
per
unit
volume
(14.22)
6E
The remaining terms in the modified principal stress equations are shear stress terms (i.e.
functions of principal stress differences in the various planes) and these are the only stresses
which give rise to distortion of the stressed element. They are therefore termed
distortional
or
deviatoric
stresses.
Now
total strain energy per unit volume
=
shear strain energy per unit volume
+
volumetric strain
i.e.
Therefore shear strain energy per unit volume is given by:
energy per unit volume
u,
=
us
+
U”
us
=
U,-U,
1
(1
-
2v)
+
0;
+
03
-
2v(n102
+
~203
+
03al)]
-
~
[I
(61
+
62
+
OS)~I
i.e.
Us
=
-[a2
6E
2E

414.17
Complex Strain and the Elastic Constants
387
This simplifies to
us
=
-
(l+
[(a,
-
a2)z
+
(a2
-
a3)2
+
(63
-
fJ1)2]
6E
and, since
E
=
2G
(1
+
v),
1
12G
1
6G
us
=
-
[a,
-
02
)2
+
(a2
-
a3
l2
+
(a3
-
0,
121
(14.23a)
or, alternatively,
Us
=
-
[d
+
0:
+
u:
-
(ala2
+
6263
+
0301)]
It
is
interesting to note here that even a uniaxial stress condition may
be
divided into
hydrostatic (dilatational) and deviatoric (distortional) terms as shown in Fig.
14.28.
(14.23b)
Z=Q1
QI
~-g+$$+~y+~$
A
f-
5
Principal (uniaxial)
stress
Hydrostotic
stresses
Deviatoric
stresses
Fig.
14.28.
Resolution
of
uniaxial stress into hydrostatic and deviatoric components.
Examples
Example
14.1
When a bar
of
25
mm diameter is subjected to an axial pull
of
61
kN
the extension
on
a
50
mm gauge length is
0.1
mm and there
is
a decrease in diameter
of
0.013
mm. Calculate the
values
of
E,
v,
G,
and
K.
Solution
load
61
x
lo3
area
$n(0.025)*
Longitudinal stress
=
-
=
=
124.2
MN/m2
0.1
x
103
=
2
10-3
Longitudinal strain
=
extension
- -
original length
lo3
x
50
stress
124.2
x
lo6
strain
2
x
io+
Young’s modulus
E
=
-
=
=
62.1
GN/m2
change in diameter
0.013
x
lo3
=
0.52
x
10-3
- -
-
Lateral strain
-
original diameter
lo3
x
25
0.52
x
10
-
3
=
0.26
-
lateral strain
Poisson’s ratio
(v)
=
-
longitudinal strain
2
x

Mechanics
of
Materials
388
Now
Also
E
E=2G(l+v)
.*.
G=-
2(1+
v)
62.1
x
109
G=
=
24.6
GN/m2
2(
1
+
0.26)
E
3(1
-
2~)
E
=
3K(l-2~)
.'.
K
=
62.1
x
109
K=
=
43.1
GN/m2
3
x
0.48
Example
14.2
A
bar of mild steel 25 mm diameter twists 2 degrees in a length of 250 mm under a torque of
430 N
m.
The same bar deflects
0.8
mm when simply supported at each end horizontally over
a span of
500
mm and loaded at the centre of the span with
a
vertical load of 1.2 kN. Calculate
the values of
E,
G,
K
and Poisson's ratio
v
for the material.
Solution
a a
J
=
-D4
=
-
(0.025)4
=
0.0383
x
m4
32 32
a
Angle of twist
8
=
2
x
-
=
0.0349 radian
180
T
ce
.
TL
JL
J8
From the simple torsion theory
-
=
-
..
G=-
430
x
250
x
lo6
0.0349
x
lo3
x
0.0383
G=
=
80.3
x
lo9
N/m2
=
80.3
GN/m2
For
a simply supported beam the deflection at mid-span with central load Wis
WL3
6=-
48EI
Then
WL3
E=---
and
4861
a
x
I
=
-D4
=
-
(0.025)4
=
0.0192
x
m4
6464
1.2
x
103
x
(0.5)3
x
106
x
103
E=
=
203
x
lo9
N/mZ
48
x
0.0192
x
0.8
=
203
GN/mZ

Complex Strain and the Elastic Constants
389
Now
..
Also
E
2G
E=2G(l+v)
.'.
v=--l
1
=
0.268
203
2
x
80.3
v=--
E
3(1
-
2~)
E
=
3K(1
-
2~)
.'.
K=-
203
x
109
K=
=
146
x
lo9
N/mZ
3(1-0.536)
=
146
GN/mZ
Example
14.3
A rectangular bar of metal 50
mm
x
25 mm cross-section and 125 mm long carries a tensile
load of
100
kN along its length, a compressive load
of
1 MN on its 50
x
125 mm faces and a
tensile load of
400
kN on its 25
x
125 mm faces.
If
E
=
208 GN/mZ and
v
=
0.3, find
(a) the change in volume
of
the bar;
(b) the increase required in the
1
MN load
to
produce no change in volume.
Solution
load
area 50
x
25
100
x
lo3
x
lo6
fJ,=--
-
=
80MN/m2
fJy
=
=
128MN/mZ
6,
= =
-
160 MN/m2 (Fig. 14.29)
400
x
103
x
io6
125
x
25
-
1
x
lo6
x
106
125
x
50
Fig.
14.29.
From $14.6
V
change in volume
=
-
(6,
+
Cy
+
6,)
(1
-
2v)
E
- -
(125
50
25)
10-9[80
+
128
+
(-
160)]106
x
0.4
208
x
109
125
x
50
x
25
x
48
x
0.4
208
x
1OI2
m3
=
14.4mm3
- -
i.e. the bar increases in volume by 14.4 mm3.

390
Mechanics
of
Materials
(b) If the
1
MN load is
to
be changed, then
6,
will
be
changed; therefore the equation for
the change in volume becomes
(125
x
50
x
25)
change in volume
=
0
=
10-9(80
+
128
+
a,)106
x
0.4
208
x
109
Then
0
=
80+128+a,
6,
=
-
208
MN/m’
Now
..
load
=
stress
x
area
new load required
=
-
208
x
lo6
x
125
x
50
x
=
-
1.3
MN
Therefore the compressive load of
1
MN must
be
increased
by
0.3
MN
for no change in
volume to occur.
Example
14.4
A
steel bar
ABC
is of circular cross-section and transmits an axial tensile force such that the
total change in length is
0.6
mm. The total length of the bar is
1.25
m,
AB
being
750
mm and
20
mm diameter and
BC
being
500
mm long and 13’mm diameter (Fig.
14.30).
Determine for
the parts
AB
and
BC
the changes in (a) length, and (b) diameter. Assume Poisson’s ratio
v
for
the steel to
be
0.3
and Young’s modulus
E
to be
200
GN/m’.
Fig.
14.30.
Solution
(a) Let the tensile force be
P
newtons.
Then
=-
MNIm’
P
-
load
stress in
AB
=
-
-
area
)n(0.02)2
loon
=-
MN/m2
P
stress in
BC
=
tn(0.013)’ 42n

Complex Strain and the Elastic Constants
39
1
Then
and
..
..
Then
and
P
=
-
x
10-6
stress
P
x 106
strain in
AB
=
-- -
E
ioonx2~x 109 2on
=
P
x 10-6
P
x
lo6
42n x 200 x
lo9
strain in
BC
=
8.471
x 750
x
lo-’
=
11.95P
x
P
x
change in length of
AB
=
20n
change in length of
BC
=
x 500 x
10-3
=
i8.95p x
10-9
8.4~
total change in length
=
(11.95P+ 18.95P)10-9
=
0.6
x
lo-’
P(11.95
+
18.95)10-9
=
0.6
x
=
19.4
kN
0.6
x
109
103
x
30.9
P=
change in length
of
AB
=
19.4 x
lo3
x
11.95 x
=
0.232 x
m
=
0.232
mm
change in length
of
BC
=
19.4
x
lo3
x
18.95
x
=
0.368 x
=
0.368
mm
(b)
The lateral (in this
case
“diametral”) strain can
be
found from the definition of
Poisson’s ratio
v.
lateral strain
longitudinal strain
V=
lateral strain
=
strain on the diameter
(=
diametral strain)
=
v
x longitudinal strain
VP
x
0.3 x 19.4 x
lo3
-
-
Lateral strain on
AB
=
2011 20n x
lo6
=
92.7 x
=
92.7
p)
compressive
VP
x
0.3
x
19.4 x
lo3
8.4n x
lo6
- -
Lateral strain on
BC
=
8.4 x
n
=
220.5 x
(=
220.5
pe)
compressive
Then, change in diameter
of
AB
=
92.7 x
x
20 x
lo-’
=
1.854
x
low6
=
0.00185
mm
and change in diameter
of
BC
=
220.5
x
=
2.865
x
x
13 x
=
0.00286
mm
Both these changes are
decreases.
392
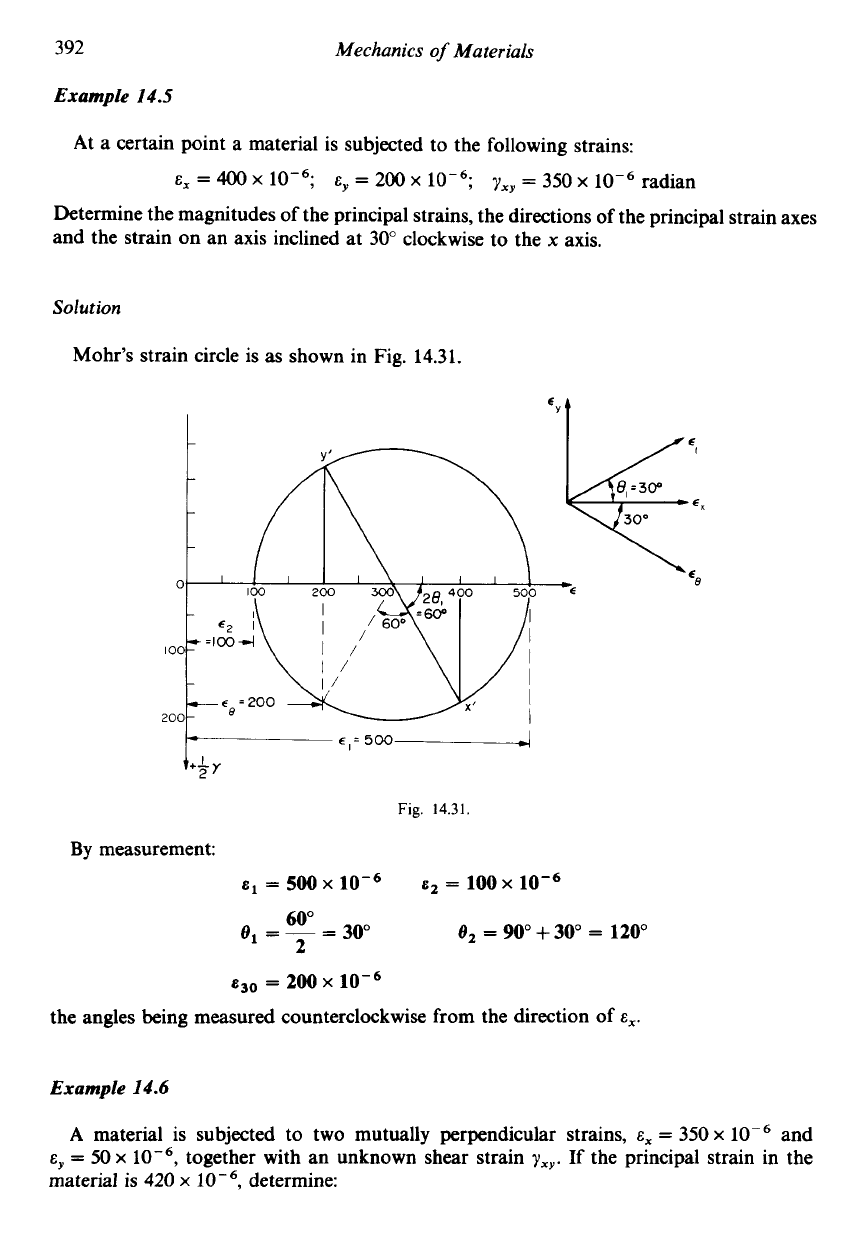
Example
14.5
Mechanics
of
Materials
At
a
certain point a material is subjected to the following strains:
E,
=
400
x
E,
=
200
x
y,,
=
350
x
radian
Determine the magnitudes
of
the principal strains, the directions
of
the principal strain axes
and the strain on an axis inclined at
30"
clockwise to the
x
axis.
Solution
Mohr's strain circle is
as
shown in Fig.
14.31.
Fig.
14.31.
By measurement:
&I
=
500
x
e,
=
-
=
300
E2
=
100
x
e,
=
900
+
300
=
1200
60"
2
=
200
x
the angles being measured counterclockwise from the direction of
E,.
Example
14.6
A
material is subjected to two mutually perpendicular strains,
E,
=
350
x
and
together with an unknown shear strain
y,,.
If
the principal strain in the
E,
=
50
x
material
is
420
x
determine:
