Hearn E.J. Mechanics of Materials. Volume 1
Подождите немного. Документ загружается.

Complex
Stresses
343
The shear stress on the oblique plane is then given by eqn. (13.2):
T@
=
ioy
sin 28
=
3
x
79.6
x
lo6
x
sin
104"
56
=
38.6
x
lo6
The required shear
stress
is
38.6
MN/rnZ.
Example
13.2
(AIB)
Under certain loading conditions the stresses in the walls of a cylinder are as follows:
(a) 80 MN/mZ tensile;
(b)
30 MN/mZ tensile at right angles to (a);
(c) shear stresses of 60 MN/m2 on the planes on which the stresses (a) and
(b)
act; the shear
Calculate the principal stresses and the planes on which they act. What would
be
the effect
on these results if owing to a change
of
loading (a) becomes compressive while stresses (b)
and (c) remain unchanged?
couple acting on planes carrying the 30 MN/m' stress is clockwise in effect.
Solution
Fig.
13.23.
The principal stresses are given
by
the formula
c1
and
oz
=$(o,+oy)f)J[(ox-oy)2+47,2y]
=
3
(80
+
30)
=
55
5J(25
+
144)
=
55+65
$J[
(80
-
30)'
+
(4
x
602)]
o1
=
120MN/m2
o2
=
-
10MN/mZ
(i.e. compressive)
..
and

344
Mechanics
of
Materials
The planes on which these stresses act can
be
determined from eqn.
(13.14),
i.e.
6
-6,
tan
8,
=
P
ZXY
120
-
80
tan
8,
=
____
-
-
0.6667
60
..
e,
=
330 41'
-
10- 80
60
=
1.50
Also tan
8,
= =
..
8,
=
-
56" 19 or 123" 41'
N.B.-The resulting angles are at
90"
to each other as expected.
If the loading is now changed
so
that the
80
MN/m' stress becomes compressive:
6,
=
f
(
-
80+ 30)+*J[
(
-80- 30)'
+
(4
x
60')]
=
-
25
+
5J(
121
+
144)
=
-
25
+
81.5
=
56.5
MN/m2
o2
=
-25-81.5
=
-
106.5MN/m2
and
Then tan8,
=
56.5
-
(
-
80)
=
2.28
60
and
8,
=
66
19
8,
=
66"
19'
+
90
=
156" 19
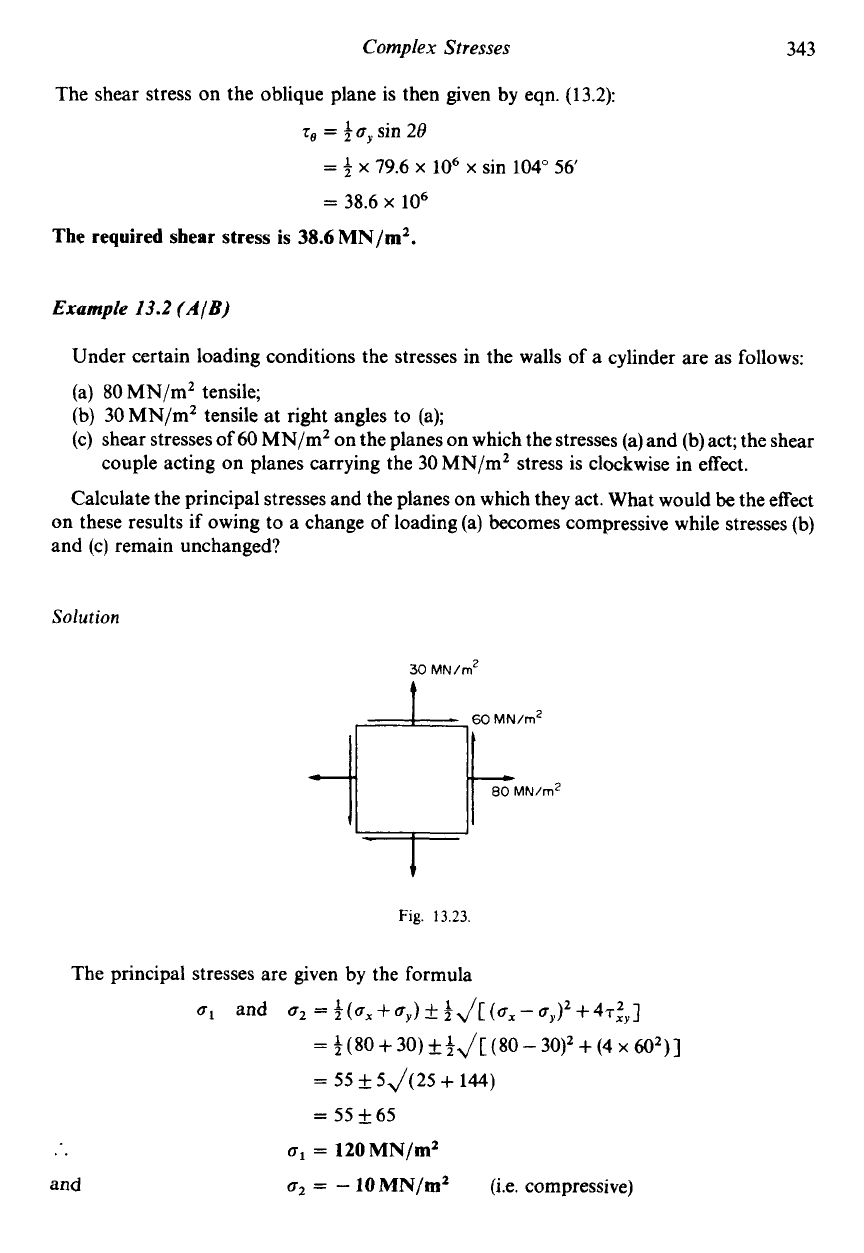
Mohr's circle
solutions
In the first part
of
the question the stress system and associated Mohr's circle are as drawn
By measurement:
in Fig.
13.24.
o1
=
120MN/m2 tensile
6'
=
10MN/m2 compressive
8,
=
34" counterclockwise from
BC
8,
=
124" counterclockwise from
BC
and
When the
80
MN/m' stress is reversed, the stress system is that in Fig.
13.25,
giving Mohr's
The required values are then:
circle as drawn.
o1
=
56.5MN/m2 tensile
o2
=
106.5 MN/m' compressive
8,
=
66" 15' counterclockwise to
BC
and
8,
=
156" 15' counterclockwise to
BC
Complex Stresses
30
345
=
120
MN/m2
-----I
u2=-10
MN/rn2
Fig.
13.24.
30
t
II
-80
-40
r-_u2=-106.5
MN/rn2,,
u,
=56.5
MN/rnq
Fig.
13.25
Example
13.3
(B)
A
material
is
subjected to two mutually perpendicular direct stresses
of
80
MN/mZ tensile
and
50
MN/mZ compressive, together with a shear stress
of
30
MN/mZ. The shear couple
acting on planes carrying the
80
MN/m2 stress is clockwise in effect. Calculate
346
Mechanics
of
Materials
the
the
the
magnitude and nature
of
the principal stresses;
magnitude
of
the maximum shear stresses in the plane
of
the given stress system;
direction
of
the planes on which these stresses act.
Confirm your answer by means
of
a Mohr’s stress circle diagram, and from the diagram
determine the magnitude
of
the normal stress on a plane inclined at
20”
counterclockwise to
the plane on which the
50
MN/m’ stress acts.
Solution
80
MN/m2
t
Fig.
13.26.
(a) To find the principal stresses:
u1
and
o2
=
+(ox
+
by)
++&ox
-
o,)*
+
~TZ,,]
=
+(
-
50+80)f+J[(
-
50
-
80)’
+
(4
x
9OO)]
=
5[3
f
J(169
+
36)]
=
5[3
f
14.311
..
u1
=
86.55
MN/mZ
o2
=
-
56.55
MN/m’
The principal stresses are
86.55 MN/m2 tensile and 56.55 MN/m2 compressive
(b)
To find the maximum shear stress:
01
-
~2
86.55
-
(-
56.55) 143.1
-
-
-
71.6
MN/m2
7max=
~
-
2 2 2
Maximum shear stress
=
71.6MN/m2
(c) To find the directions
of
the principal planes:
0
-6,
86.55-(-50)
30
tan8,
=
=
TXY
136.55
30
=
-
=
4.552

Complex
Stresses
347
..
e,
=
77036
..
e2
=
770
36'
+
900
=
1670 36
The principal planes are inclined at
77"
36' to the plane on which the
50
MN/m2 stress acts.
The maximum shear planes are at
45"
to the principal planes.
Mohr's
circle solution
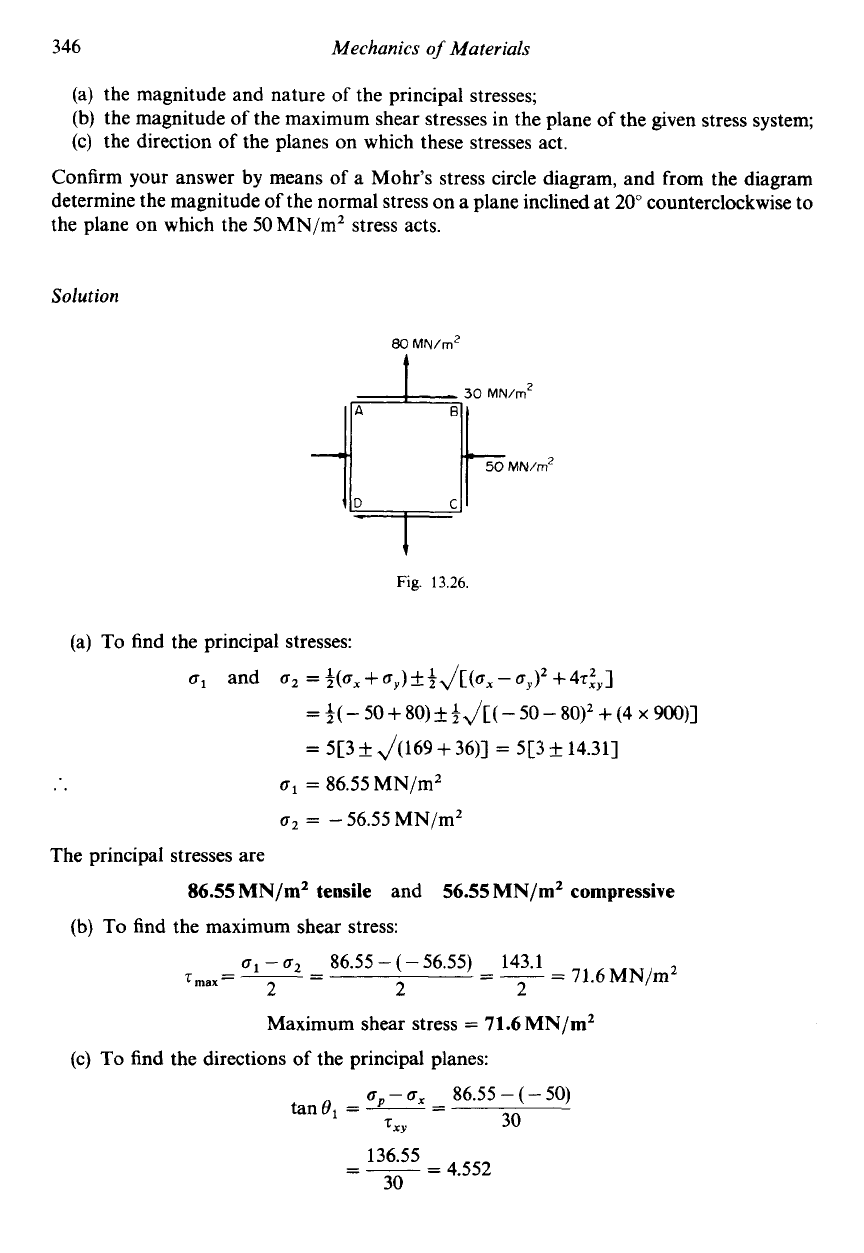
The stress system shown in Fig. 13.26 gives the Mohr's circle in Fig. 13.27.
80
MNh2
Fig.
13.27.
By measurement
c,
=
87MN/mZ tensile
c2
=
57 MN/mZ compressive
T,,,
=
72 MN/m2
and
The direct or normal stress on a plane inclined at 20" counterclockwise to
BC
is obtained
by
c
=
16 MN/mZ compressive
measuring from
This gives
on the Mohr's circle through 2
x
20"
=
40"
in the same direction.

348
Mechanics
of
Materials
Example
13.4
(B)
At a given section a shaft is subjected to a bending stress
of
20 MN/m2 and a shear stress of
40
MN/m2. Determine:
(a) the principal stresses;
(b) the directions
of
the principal planes;
(c) the maximum shear stress and the planes on which this acts;
(d) the tensile stress which, acting alone, would produce the same maximum shear stress;
(e) the shear stress which, acting alone, would produce the same maximum tensile
principal stress.
Solution
(a)
The bending stress is a direct stress and
can
be treated as acting on the
x
axis,
so
that
a,
=
20 MN/m2; since no other direct stresses are given,
a,
=
0.
Principal stress
0,
=
+(a,+a,)+iJ~(~,--,)~
+42:,1
=
3
x
20
+
3J[202
+
(4
x
402)]
=
10+
5J(68)
=
10+ 5
x
8.246
=
51.23MN/mZ
and
a2
=
10-41.23
=
-
31.23 MN/m2
(b) Then
a
-a,
51.23 -20 31.23
-
o.7808
=--
40
40
tan8,
=
JL-
=
ZXY
..
el
=
370
59'
and
-
31.23
-
20
-
51.23
-
1.2808
-
--=
40 40
tan8,
=
..
O2
=
-
52"
1'
or 127"
59'
both angles being measured counterclockwise from the plane on which the 20 MN/m2 stress
acts.
(c) Maximum shear stress
aI
-
0,
2
51.23
-
(-
31.23)
2
Zmax=
~
=
82.46
2
=
__
=
41.23 MN/m2
This acts on planes at 45" to the principal planes,
i.e.
at
82"59'
or
-7"
1'
(d) Maximum shear stress
zmax=
+Jc(~,
-
0,)'
+
4~2~1
Complex
Stresses
349
Thus if a tensile stress is to act alone to give the same maximum shear stress
(6,
=
0
and
maximum shear stress
=
i,/(oz)
=
30,
ZXY
=
0):
41.23
=
$0,
i.e.
ox
=
82.46 MN/m2
The required tensile stress is
82.46
MN/mZ.
(e)
Principal stress
81
=
t(u,+by)+fJ~(ux-by)2+4?zyl
01
=
3J(4?3
=
Txy
Thus if a shear stress is to act alone to give the same principal stress
(0,
=
uY
=
0):
51.23
=
rxY
The required shear stress is
51.23 MN/m2.
Mohr's
circle
solutions
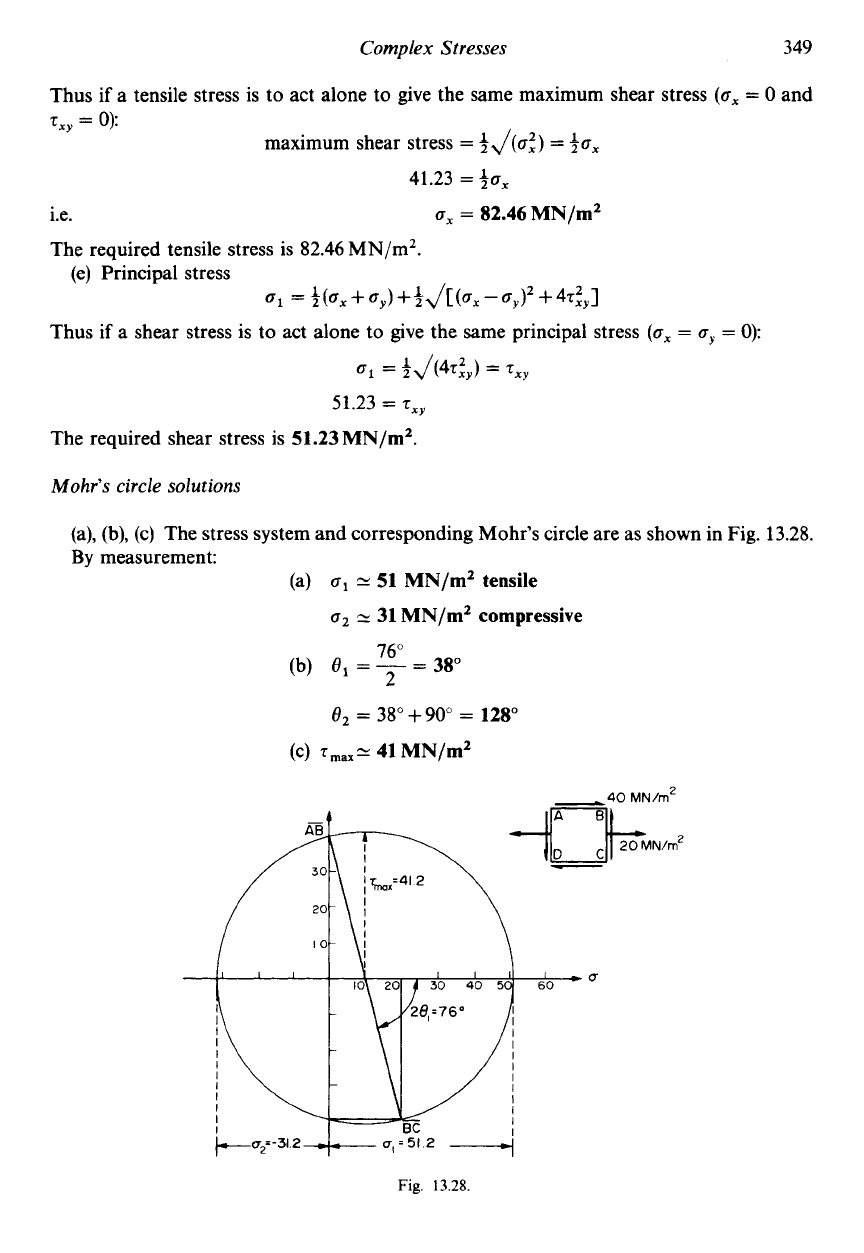
(a),
(b),
(c) The stress system and corresponding Mohr's circle are as shown in Fig.
13.28.
By measurement:
(a)
u1
N
51 MN/m2
tensile
u2
'v
31 MN/m2
compressive
76"
(b)
8,
=
-
=
380
2
82
=
38"
+
90"
=
128"
(c)
rrnaX=
41 MN/m2
Fig.
13.28.

350
Mechanics
of
Materials
Angle
of
maximum shear plane
-
83"
166
2
---
-
(d)
If
a tensile stress
(T,
is to act alone to give the same maximum shear stress, then
(T,,
=
0,
z,,,
=
0
and
zmax
=
41
MN/mZ. The Mohr's circle therefore has a radius
of
41
MN/mZ and
passes through the origin (Fig.
13.29).
Hence the required tensile stress is
82
MN/rn2.
r
60
t
Fig.
13.29.
(e)
If
a shear stress is to act alone to produce the same principal stress,
ox
=
0,
(T,,
=
0
and
u1
=
51
MN/m2. The Mohr's circle thus has its centre at the origin and passes through
u
=
51
MN/m2 (Fig.
13.30).
Hence the required shear stress
is
51
MN/rnZ
.
t
I
Fig.
13.30.

Complex
Stresses
35
1
Example
13.5
(B)
At a point in a piece of elastic material direct stresses of
90
MN/m2 tensile and 50 MN/mZ
compressive are applied on mutually perpendicular planes. The planes are also subjected
to
a
shear stress.
If
the greater principal stress is limited to 100MN/mZ tensile, determine:
(a)
the value
of
the shear stress;
(b)
the other principal stress;
(c) the normal stress on the plane of maximum shear;
(d) the maximum shear stress.
Make a neat sketch showing clearly the positions of the principal planes and planes of
maximum shear stress with respect to the planes
of
the applied stresses.
Solution
(a) Principal stress
crl
=
$(ax
+
by)
+
$J[(o,
-
cry)'
+
47,2,]
This is limited to 100MN/mZ; therefore shear stress
T~~
is given by
100
=
$(90
-
50)
+
$J[
(90
+
50)2
+
47,2,]
200
=
40
+
lOJC14'
+
O.Mr$]
..
..
=
38.8
MN/mZ
The required shear stress is 38.8 MN/m2.
(b) The other principal stress
(r2
is given by
62
=3(6x+6y)-3J[(6,-6Y)2
+47'$]
40-
OJ(2
6)
2
=$[(90-50)-10J(142+60)]
=
40- 160
2
-
-
-60
MN/m2
The other principal stress is
60
MN/m2 compressive.
(c) The normal stress on the plane of maximum shear
a1+a2
100-60
=-=-
2
2
=
20MN/m2
The required normal stress is
20
MN/m2 tensile.
(d) The maximum shear stress
is
given by
61-62
100+60
Tmax=
~
=
____
2
2
=
80MN/mZ
The maximum shear stress is 80 MN/m'.
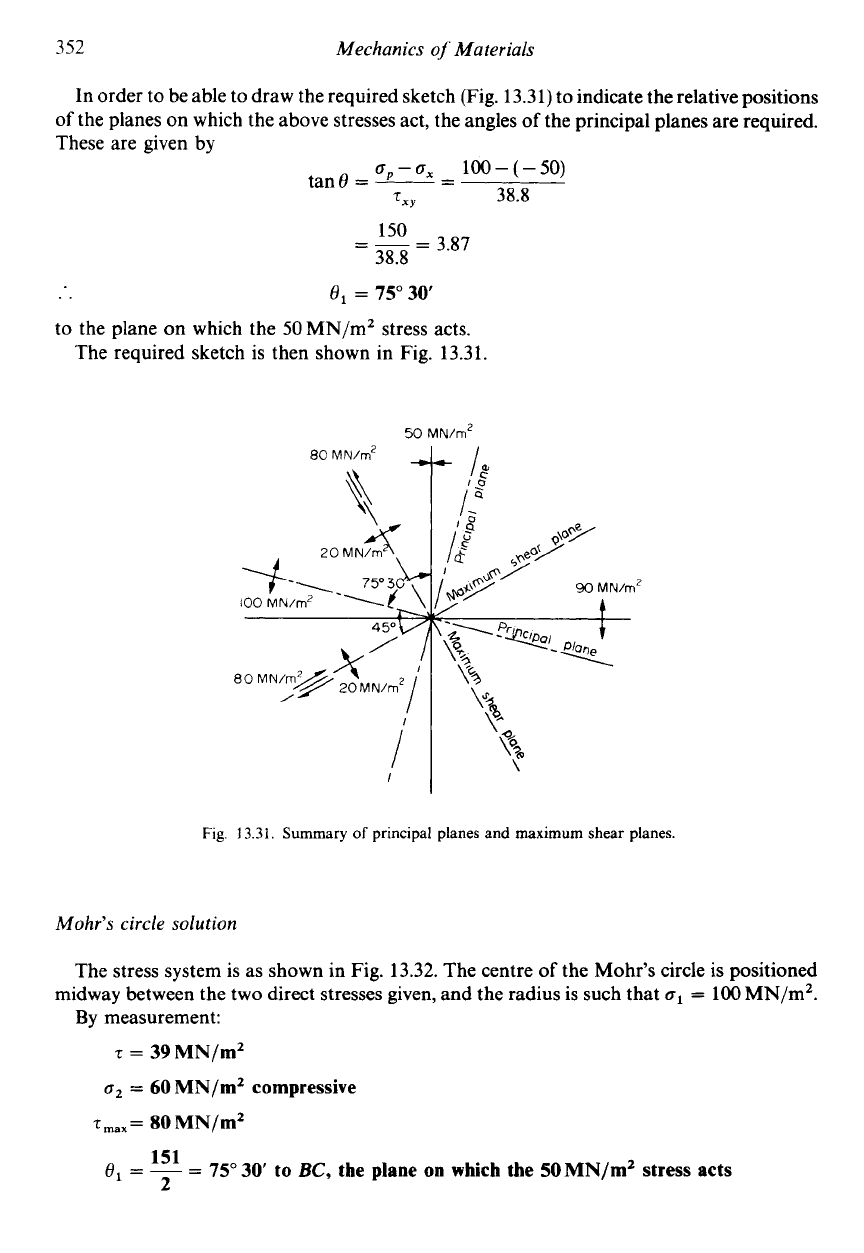
352
Mechanics
of
Materials
In order to be able to draw the required sketch (Fig. 13.31) to indicate the relative positions
of
the planes on which the above stresses act, the angles
of
the principal planes are required.
These are given by
0
-0
100-(-50)
tang
= =
TXY
38.8
..
el
=
750
30’
to the plane on which the
50
MN/mZ stress acts.
The required sketch is then shown in Fig. 13.31.
50
MN/m‘
Fig.
13.31.
Summary
of
principal planes and maximum shear planes.
Mohr’s
circle solution
The stress system is as shown in Fig. 13.32. The centre
of
the Mohr’s circle is positioned
midway between the two direct stresses given, and the radius is such that
g1
=
100 MN/m2.
By measurement:
7
=
39MN/mZ
uz
=
60
MN/mZ compressive
7
max
=
80
MN/mz
151
2
8,
=
~
=
75”
30’
to
BC,
the plane on which the 50MN/m2 stress acts
